行为阈值模型的概率研究∗
2016-04-20刘萍卢守峰谢耀漩
刘萍,卢守峰,谢耀漩
(长沙理工大学交通运输工程学院,湖南长沙 410004)
行为阈值模型的概率研究∗
刘萍,卢守峰,谢耀漩
(长沙理工大学交通运输工程学院,湖南长沙 410004)
摘要:行为阈值模型通过阈值曲线划分车辆跟驰行驶状态。已有的Wiedemann74模型只知道行为分区,不知道各行为分区的概率。文中通过路侧激光检测器采集交通流数据,分车道对车间距、速度差进行数据处理,拟合交通流的车间距、速度差的概率函数R(Δv,Δx);利用标定的行为阈值曲线对概率分布函数进行积分,得到行为阈值模型的概率,从而同时得到车辆的跟驰行驶状态及其概率。
关键词:公路交通;交通流;行为阈值;跟驰行驶
1 行为阈值模型简介
行为阈值模型以驾驶员生理和心理行为作为理论基础,是一种生理-心理模型。心理学家通过研究,将人类反应一般模式总结为PIEV(Preception Intellection Evaluation Volition),即察觉—推理—评价—行动,驾驶员的驾驶行为反应符合PIEV模式。1974年Wiedemann提出Mission模型,深入研究了车辆驾驶行为的阈值界限,并给出车辆跟驰行为阈值曲线(如图1所示)。广泛使用的交通仿真软件VISSIM的车辆跟驰模型使用的就是Wiedemann行为阈值模型,其中Wiedemann74模型适用于城市道路,Wiedemann99模型适用于高速公路。该文研究Wiedemann74模型。
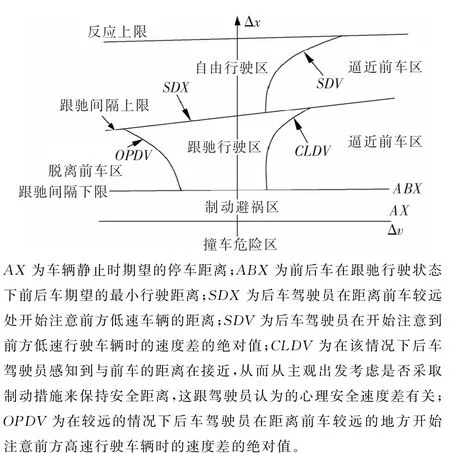
图1 Wiedemann跟驰行为阈值分区示意图
车辆跟驰状态分为5类,即自由行驶区、逼近前车区、跟驰行驶区、脱离前车区和制动避祸区,但行为阈值模型只是划分车辆跟驰行驶的状态界限,无法得知处于各区间的分布概率。为此,该文利用路测激光检测器采集断面交通流数据,对每个车道的速度差、车间距进行数据处理,利用1stopt软件对速度差Δv和车头间距Δx的概率函数R(Δv,Δx)进行拟合。利用标定的行为阈值曲线对概率分布函数进行积分,得到行为阈值模型的概率,从而同时得到车辆的跟驰行驶状态及其概率。
2 车辆跟驰行驶特性分析
利用路侧激光检测器对长沙市东二环南往北和北往南两个方向的断面交通流进行数据采集,时间为工作日15:30—18:00,连续测量2.5 h,共得到6条车道16 265个有效车辆样本数据。每个行驶方向共3条车道,其中外侧车道标为车道一,靠近中央分隔带的车道标为车道三,中间车道标为车道二。路侧激光检测器得到的数据包括各车道车辆行驶速度和时间,通过数据处理得到每条车道的流量和速度关系(如图2所示)及各车道前后车速度差Δv和车头间距Δx,其中速度差Δv取值范围为-30~30 km/h,车头间距的取值范围为8~148 m,并对速度差Δv和车头间距Δx分别以5 km/h、10 m为单位的步长进行离散,得到双向6条车道的速度差Δv和车头间距Δx的概率(如图3~6所示)。
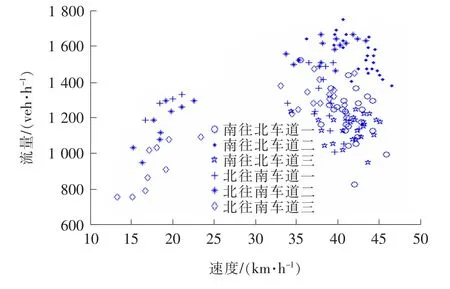
图2 各车道流量-速度散点图
由数据处理得到南往北车道一、车道二和车道三的车流量分别为1 395、1 773、1 163 veh/h,北往南车道一、车道二和车道三的车流量分别为1 305、1 391、1 136 veh/h,调查期间长沙市东二环两方向交通流量基本一致。南往北3条车道的车辆密度平均为92 veh/km,北往南3条车道的车辆密度平均为125 veh/km。从图2可知南往北方向3条车道平均速度均在35 km/h以上、北往南3条车道部分时段平均速度为15~25 km/h,说明南往北车辆通行速度较大,北往南车辆运行速度较小。
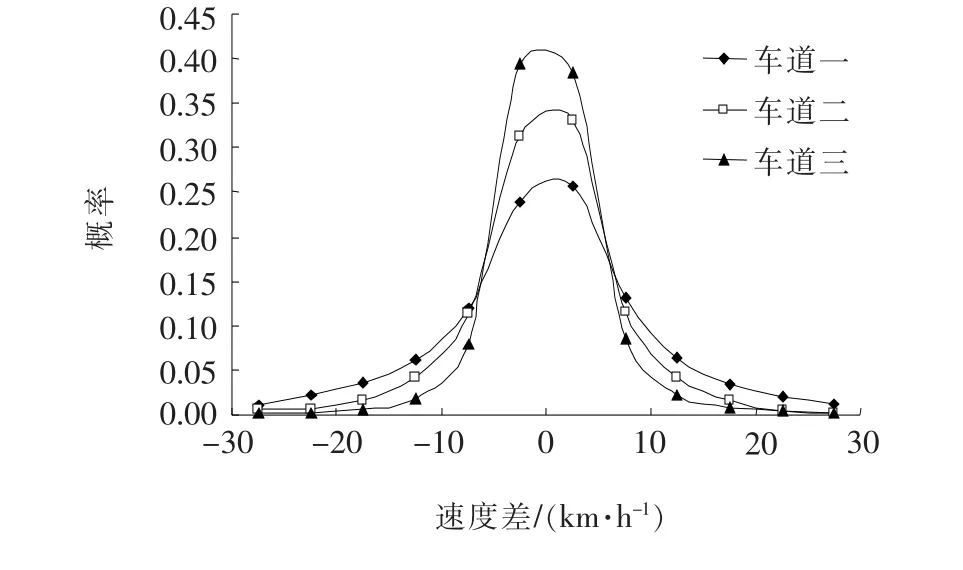
图3 南往北方向每车道相邻车速度差概率

图4 北往南方向每车道相邻车速度差概率
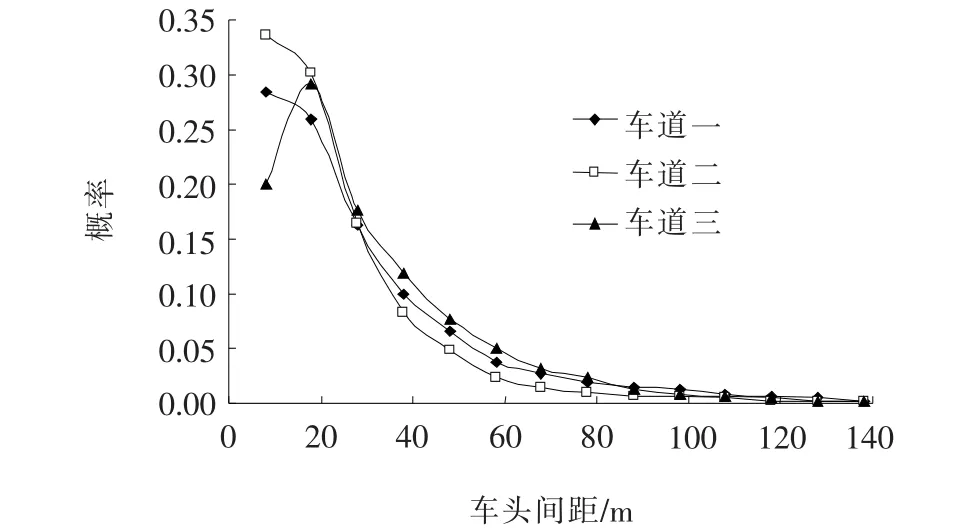
图5 南往北方向每车道相邻车车头间距概率
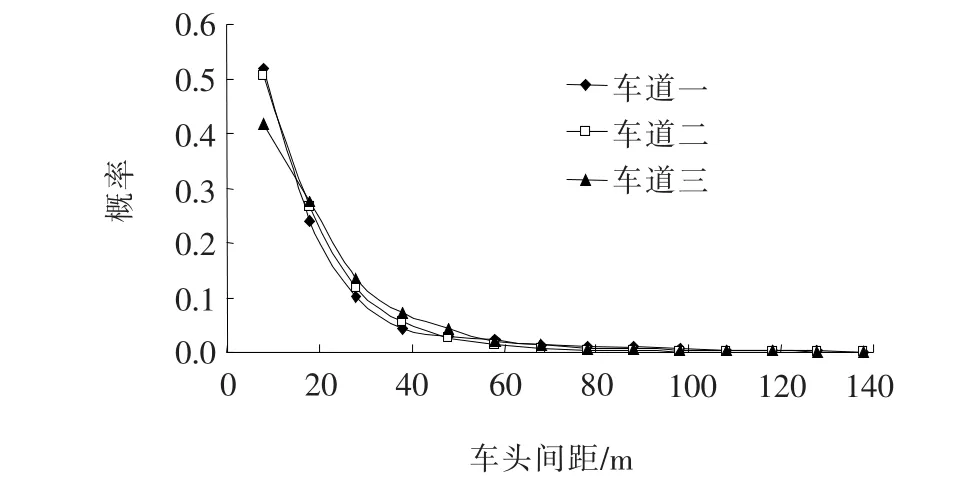
图6 北往南方向每车道相邻车车头间距概率
根据图2,长沙市东二环两方向6条车道在车辆顺畅通行时的流量均是车道二最大,表明在交通顺畅通行时驾驶员习惯性选择车道二行驶,这是由于一方面便于换道至车道一和车道三,另一方面相对于车道一受行人和公交车的影响小。
从图3和图4来看,南往北方向93.5%和北往南方向96.3%车辆的速度差为-15~15 km/h,两个方向整体车辆的速度差概率分布的相关系数为0.994 5,说明尽管两方向的交通流状态不同,但其速度差概率分布基本一致,服从正态分布。
从图5和图6来看,南往北方向95.08%和北往南方向98.08%车辆的车头间距集中在8~78 m,其中北往南方向主要分布在8~18 m,南往北方向则是较均匀地分布在8~28 m,其主要受两方向车辆密度的影响,车辆密度较大时车辆概率分布集中,反之则较均匀分布。两个方向整体车辆的车头间距概率分布的相关系数为0.9,两方向的交通状态不同,但其车头间距概率分布仍然具有相关性,服从偏正态分布。
3 速度差与车间距的联合概率函数
由南往北方向3条车道的数据通过1stopt软件进行拟合分析,得到速度差与车间距的联合概率函数R(Δv,Δx),该函数同样是以速度差和车头间距为变量得到车辆的概率,结合行为阈值模型可得到各驾驶行为区的车辆概率。通过多次尝试,采用5个参数的多项式进行拟合[如式(1)所示]。不同车道的参数取值及拟合相关系数如表1所示,各车道及断面的拟合结果如图7~10所示。
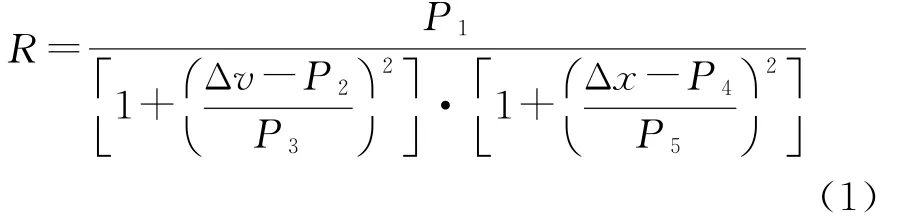
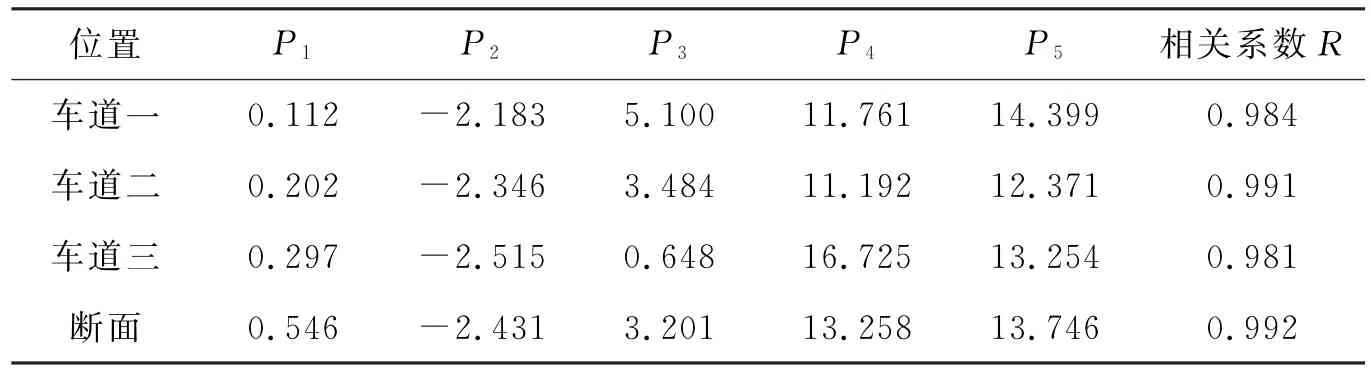
表1 南往北各车道车辆概率函数参数取值
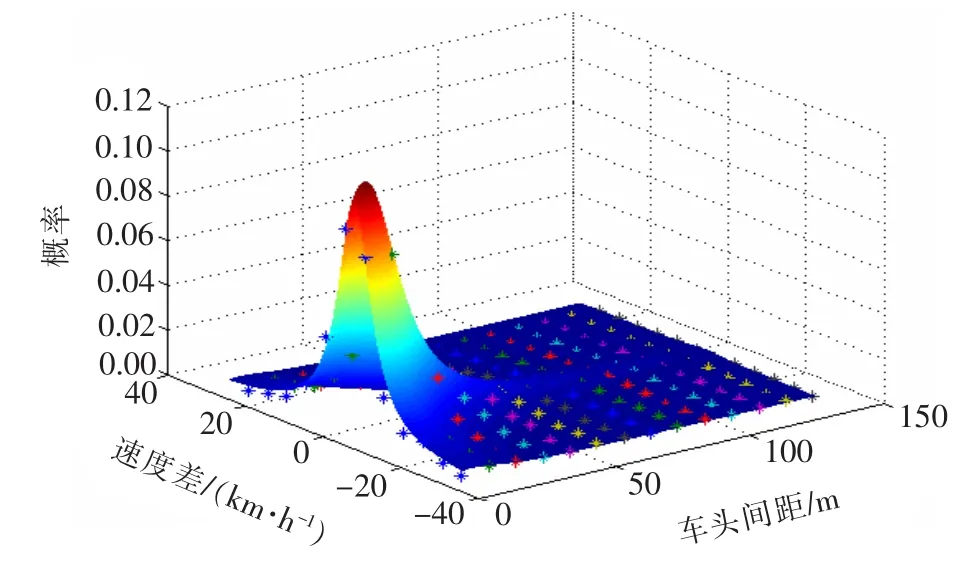
图7 车道一函数R拟合结果
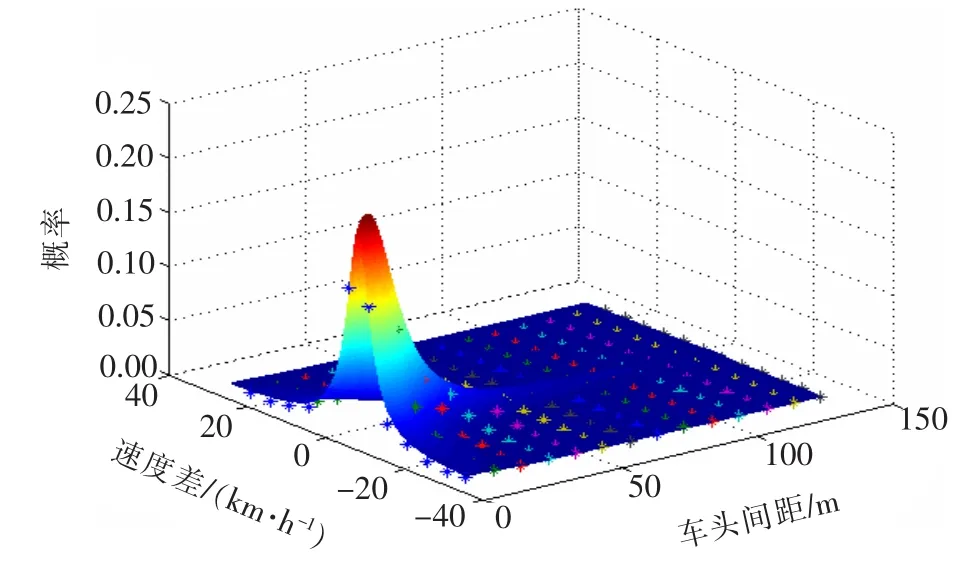
图8 车道二函数R拟合结果

图9 车道三函数R拟合结果
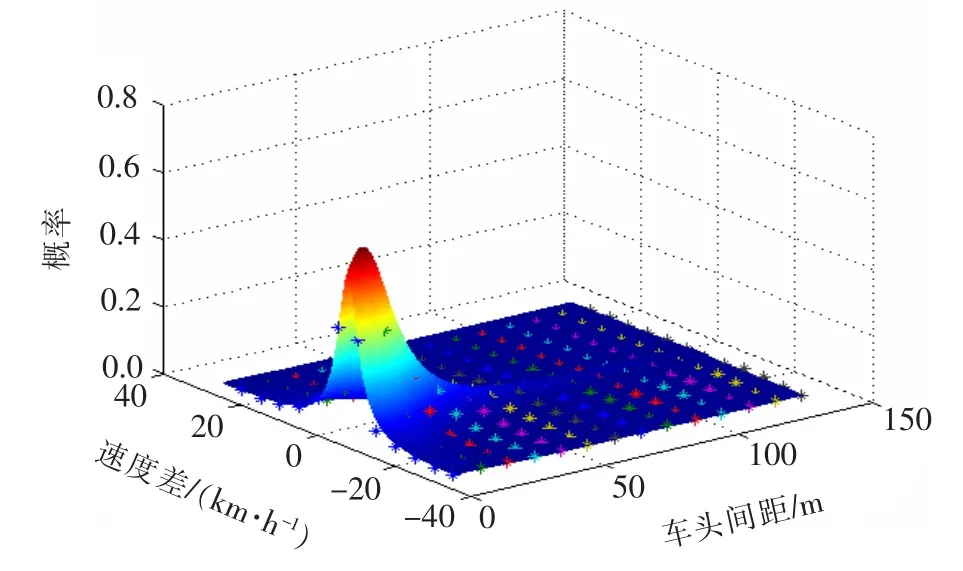
图10 断面函数R拟合结果
4 驾驶行为分区的概率分布
利用实测数据对行为阈值曲线界限的公式进行拟合得到行为阈值曲线图,对长沙市东二环南往北方向的交通数据通过1stopt软件进行处理,得到符合实际城市道路的行为阈值曲线,VISSIM软件中Wiedemann74模型的默认参数安全距离加法项取值为2、安全距离乘法项取值为3,参照文献[7]、[8]对东二环交通流的驾驶行为参数的标定修正结果,加法项取值为2.384,乘法项取值为0.61。利用路侧激光检测器数据对驾驶行为阈值曲线进行拟合,结果如表2所示。
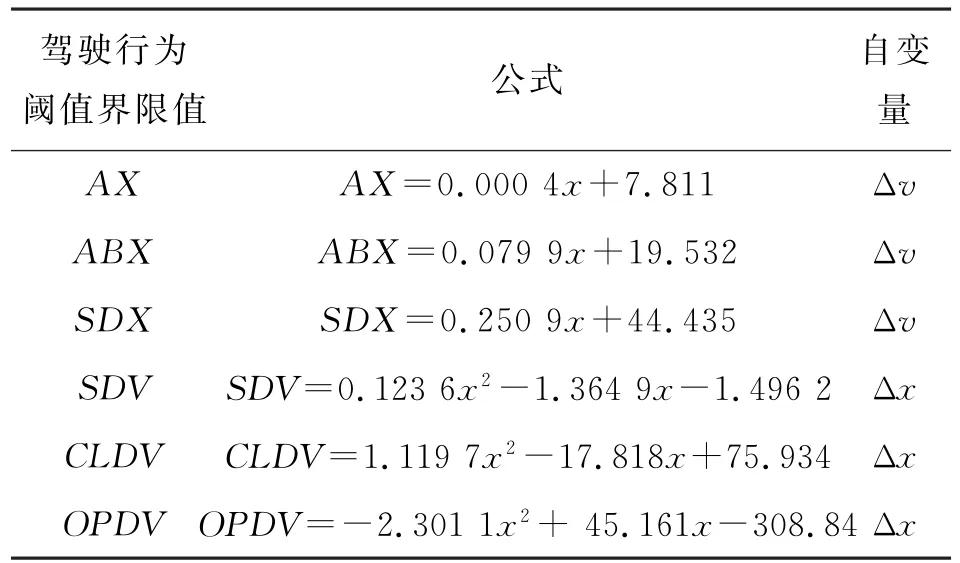
表2 行为阈值曲线表达式
利用表3所示行为阈值曲线对第3节速度差与车间距的联合概率分布函数进行积分,得到每条车道和断面的驾驶行为分区概率:

式中:P为概率;upperlimit为反应上限。
按照式(2)~(6)计算,得到东二环南往北方向交通流在各驾驶行为区域的概率(如表3所示)。
5 结语
该文使用便携式路侧激光检测仪在长沙市东二环连续采集交通流数据,通过数据处理分析得到交通流的速度差Δv、车头间距Δx、流量及密度特性,采用MATLAB、1stopt和Excel软件拟合得到三维车辆分布概率和行为阈值曲线。运用行为阈值模型结合车辆分布概率,由Δv、Δx便可知车辆的跟驰行驶状态及其分布概率。将引入车辆分布概率的行为阈值模型应用于Wiedemann74模型中,可更加切实有效地描述城市交通流。
目前仅有城市道路和高速公路有对应的模型,且不同道路条件下行为阈值模型有所差别,进一步完善行为阈值模型具有重要理论意义和实用价值。

表3 驾驶行为区域概率
参考文献:
[1]董佩明.城市快速路交通流行为阈值模型研究[D].北京:北京工业大学,2001.
[2]张清华.VISSIM微观交通仿真模型校正研究[D].北京:北京交通大学,2012.
[3]朱林波.VISSIM仿真软件中微观交通仿真模型参数校正研究[D].成都:西南交通大学,2013.
[4]费文鹏,宋国华.车辆跟驰模型的VSP和加速度分布对比分析[J].系统仿真学报,2014,26(11).
[5]徐安凤,李金莱,姚春光.非规则三维数据的曲面拟合方法[J].计算机工程与应用,2009,45(20).
[6]薛郁,董力耘,袁以武,等.考虑车辆相对运动速度的交通流演化过程的数值模拟[J].物理学报,2002,51(3).
[7]Lu S,Dai S,Liu X.A discrete traffic kinetic model-integrating the lagged cell transmission and continuous traffic kinetic models[J].Transportation Research Part C:Emerging Technologies,2011,19(2).
[8]卢守峰,王丽园.宏观标定方法在Wiedemann驾驶行为阈值研究中的应用[J].公路交通科技,2015,31(9).
[9]陶诚,黄圣国.基于TSK模型的车辆跟驰模型[J].华南理工大学学报:自然科学版,2009,37(3).
[10]张智勇.城市快速道路车辆跟驰模型研究[D].北京:北京工业大学,2002.
[11]王立锋,李正熙.基于车辆跟驰理论的交通流动力学模型与数值仿真[J].东南大学学报:自然科学版,2005,35(增刊2).
收稿日期:2015-12-25
基金项目:∗国家自然科学基金面上项目(71071024)
中图分类号:U491.2
文献标志码:A
文章编号:1671-2668(2016)02-0035-04
