具有大时滞的非线性定常大系统的无条件稳定性

韩月乔， 高存臣

(中国海洋大学数学科学学院， 山东 青岛 266100)



具有大时滞的非线性定常大系统的无条件稳定性

韩月乔， 高存臣

(中国海洋大学数学科学学院， 山东 青岛 266100)

摘要：应用Lyapunov函数分解法(即标量和的Lyapunov函数法)，结合微分方程与微分差分方程的等价性的方法(即分解等价法)，研究了具有大时滞的非线性定常大系统的无条件稳定性，得到了该系统为无条件稳定的充分性判据。本文对时滞项的研究不同于以往的小时滞，找到了使含大时滞项的系统为无条件稳定的途径，从而为这类问题的研究给出了一种新方法。

关键词：定常大系统； 大时滞； 非线性； 无条件稳定性

HAN Yue-Qiao， GAO Cun-Chen. Unconditional stability of monlinear constant large scale systems with large time delay[J].Periodical of Ocean University of China, 2016, 46(3): 134-140.

在任何实际控制系统中，由于信号的传递、变量的测量以及系统设备所具有的一些物理特性等各种因素，时滞的影响往往是不可避免的，如多级火箭发射控制信号具有时滞、电感器的感应具有时滞等。近年来，时滞系统的研究成为控制理论中的一个热点问题，引起了学者们的广泛关注[1-3]，特别是对于具有小时滞的非线性系统，已有了比较深入的研究[4-13]。其中，文献[4]研究了时滞离散广义大系统的渐近稳定性；文献[5]研究了具有时滞的非线性无穷大系统的稳定性；文献[7]研究了二阶非线性时滞微分方程的稳定性；文献[9]研究了变时滞线性系统的指数稳定性；文献[11]整合了分数时滞系统的稳定性测试。他们状态当中的时滞多为小时滞，然而，对具有大时滞的非线性大系统的研究并不多见。一般而言，由于对大时滞项中的状态xi(t-τ)的处理比较棘手，从而给问题的讨论带来一定障碍，使得大时滞系统的研究处于初始阶段。本文通过将小时滞[5-7]推广到大时滞，应用标量和的Lyapunov函数法，结合分解等价法，研究了具有大时滞的非线性定常大系统，得到了系统时滞无关的无条件稳定的充分性判据。

1预备知识

考虑具有大时滞的非线性定常大系统

(1)

其中，φi(t)∈C1([-τ,0],R)，cij,bij为实常数,i,j=1,2,…,n；τ≡Const.≥0，令

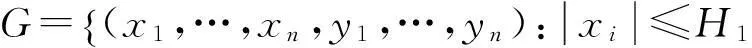
为研究方便，本文作出如下假设：

(2)

其中η是与xi，yi无关的正常数。

系统(1)中不含时滞的线性部分为

(3)

将(3)按主对角线分成l组相互无关的微分方程组

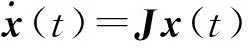
(4)

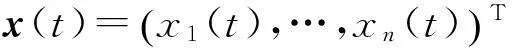
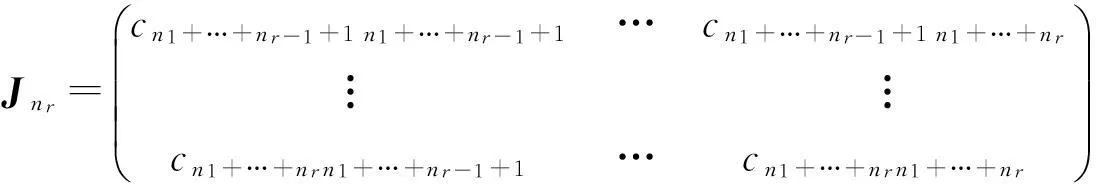
(5)

(r=1,2,…,l;n1+n2+…+nl=n)，

记

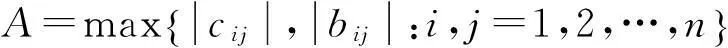
(6)

E为(3)的系数矩阵中除掉(4)的系数矩阵J后，矩阵元素的绝对值的最大值，即

E=

(7)

系统(4)中第r(r=1,2,…,l)组的微分方程组为

(8)

微分方程组(8)的特征方程为

(9)

I∈Rnr×nr为单位矩阵。

对r=1,2,…,l，代数方程(9)的Routh-Hurwitz主子行列式为

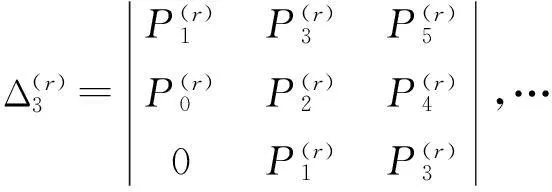
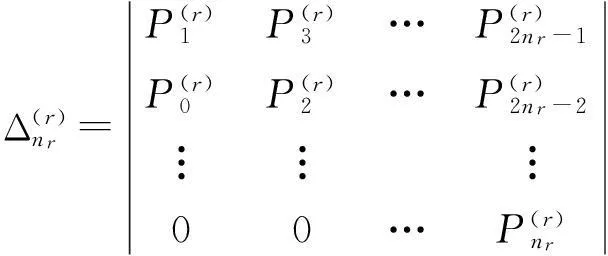
(10)

设系统(4)的特征方程(9)的特征根均具负实部，由Routh-Hurwitz定理知

2主要结果

定理1若系统(4)的零解是渐近稳定的，并设系统(1)的非线性项满足假设条件(A1)，则存在常数▽1>0,▽2>0，使当

(11)

时，对任何τ≥0，系统(1)的零解也是渐近稳定的[11-12]。其中

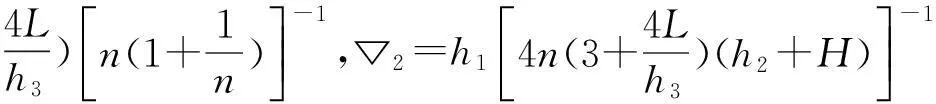
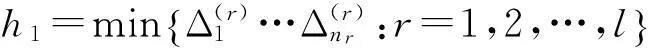
(12)

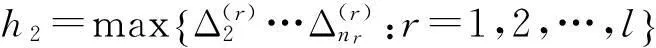
(13)

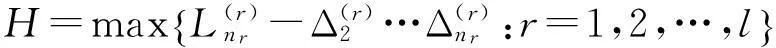
(14)

证明作l个Lyapunov函数的和式[3]

V=Vn1+…+Vnr+…+Vnl。

(15)

对(15)沿着系统(1)的积分曲线对t求导数，有

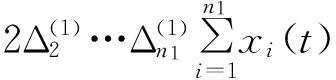
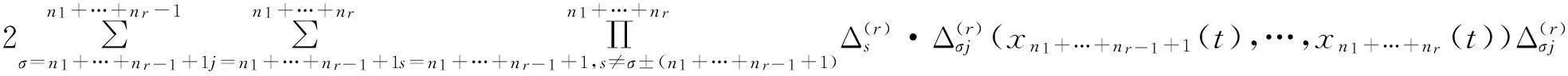
xn(t),x1(t-τ),…,xn(t-τ))]+2×

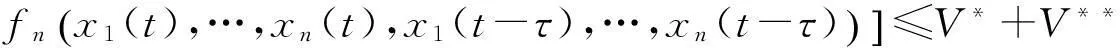
(16)

其中

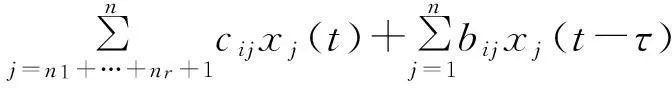
(17)

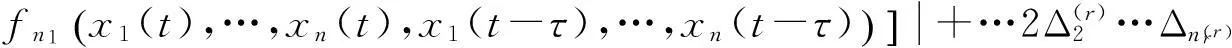
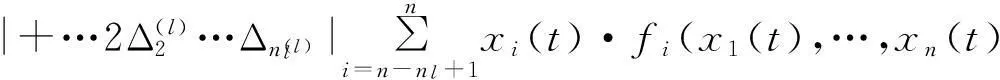
x1(t-τ),…,xn(t-τ))|+2×

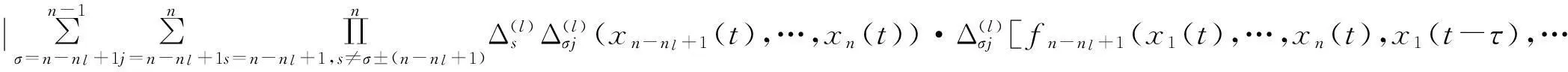
xn(t-τ)),…,fn(x1(t),…,xn(t),x1(t-τ),…,xn(t-τ)]|。

(18)

应用文献[3]第3章引理4,得到估计式

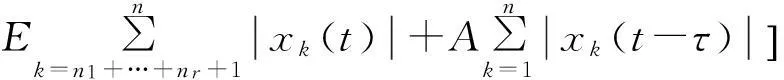
(19)

σ=n1+…+nr-1+1,…,n1+…+nr-1;j=n1+…+nr-1+1,…,n1+…+nr(r=1,2,…,l)将(19)式代入(17)式，由文献[3]第3章引理4，得

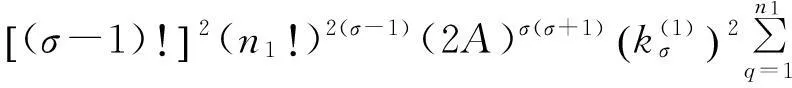
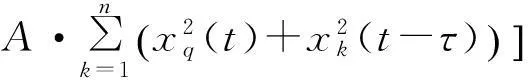
(20)

将(12)~(14)式代入(20)式中，得到

(21)

因为n=n1+…+nr+…+nl，所以少于l个n1,n2,…,nl的任意线性组合皆小于n。即

(22)

同理，对任意的r(r=2,3,…，l-1),有

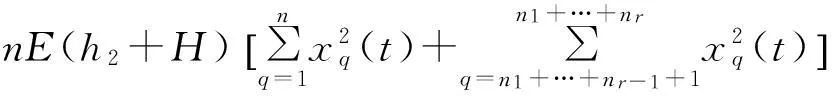
(23)

(r=2,3,…，l-1)

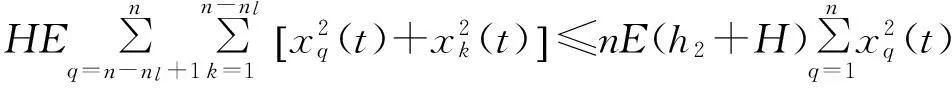
(24)

将(22)~(24)式代入(21)式中，得到

(25)

由文献[3]第3章引理5，得到

(26)

将(26)式代入(25)式，得到

V*≤

(27)

应用文献[3]第3章引理4以及假设A1)，得到

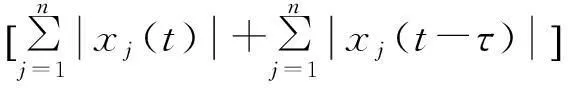
(28)

σ=n1+…+nr-1+1,…,n1+…+nr-1;j=n1+…+nr-1+1,…,n1+…+nr(r=1,2,…,l)将不等式(28)代入(18)式中，得到

V**≤

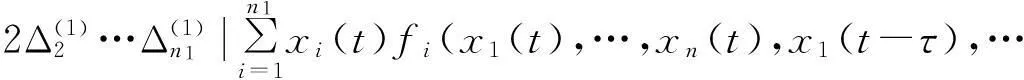
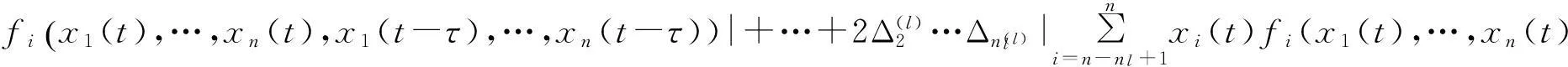
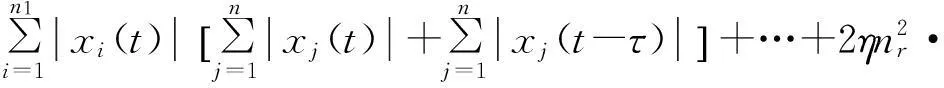
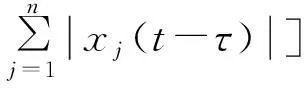
(29)

运用假设A1)，将(12)-(14)式代入(29)式中，得

V**≤

(30)

运用文献[3]第3章引理6于(30)式，得到

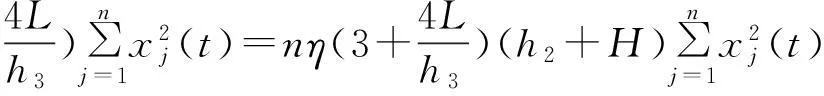
(31)

综上，得到

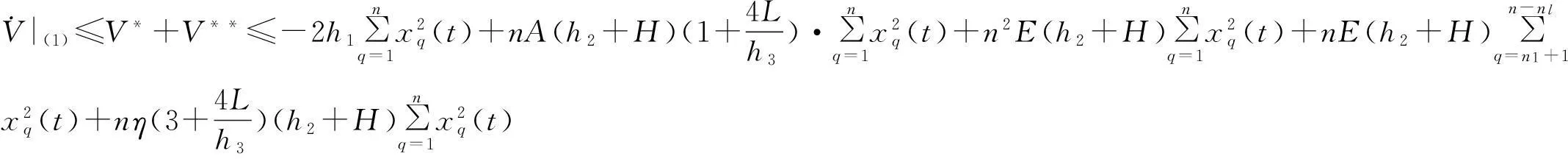
(32)

推论1对于具有大时滞的线性定常大系统

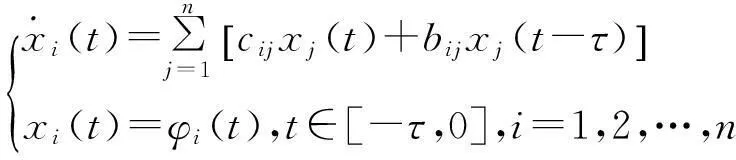
(33)

3数值例子

考虑2维具有大时滞的非线性定常系统

(34)

(35)

此时，子系统(35)的零解是渐近稳定的，由于

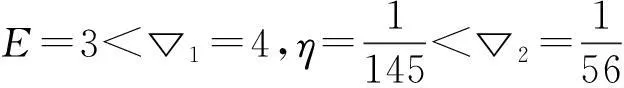
(36)

所以，由定理1知，系统(34)的零解是无条件稳定的。

系统(34)的状态曲线图形如图1所示。从图1可以看出，状态曲线x1(t)，x2(t)随着时间t的增加将会趋于0，即系统(34)是无条件稳定的。而且系统的状态曲线在0.5S内就接近0了，所以，该系统在本文定理的条件下，具有快速稳定的性能。

图1　系统(34)的状态曲线示意图

4结语

在本文，应用标量和的Lyapunov函数法，结合微分方程与微分差分方程的分解等价性方法，研究了具有大时滞的非线性定常大系统的无条件稳定性，得到了一个系统为无条件稳定的充分性判据。给出了具体的数值例子说明了研究结果的可行性和有效性。

顺便指出：利用本文的方法可以给出具有大时滞的非线性时变大系统为无条件稳定的判据，限于篇幅，将另文给出。

参考文献：

[1]文海霞. 一类时滞非线性动力系统的全局指数稳定性[J]. 科学技术与工程, 2009, 9(2): 430-432.

WenHX.Globalexponentialstabilityofaclassofnonlineardynaicalsystemswithtimedelays[J].ScienceTechnologyandEngineering, 2009, 9(2): 430-432.

[2]高存臣, 袁付顺, 肖会敏. 时滞变结构控制系统[M]. 北京：科学出版社, 2004: 1-219.

GaoCC,YuanFS,XiaoHM.Variablestructurecontrolsystemswithtimedelays[M].Beijing:SciencePress, 2004: 1-219.

[3]刘永清, 宋中昆. 大型动力系统的理论与应用(卷I) [M]. 广州：华南工学院出版社, 1988: 111-130.

LiuYQ,SongZK.TheoryanApplicationofLarge-ScalePowerSystems[M].Guangzhou：SouthernChinaInstituteofTechnology, 1988: 111-130.

[4]郑萌, 张庆灵, 朱宝彦. 时滞离散广义大系统的稳定性分析[J]. 系统工程与电子技术, 2007, 29(7): 1126-1130.

ZhengM,ZhangQL,ZhuBY.Stabilityanalysisofdiscretesingularlargescalesystemswithtimedelays[J].SystemsEngineeringandElectronics, 2007, 29(7): 1126-1130.

[5]章毅, 张毅. 非线性无穷时滞大系统的稳定性[J]. 数学季刊, 1990, 5(3): 100-101.

ZhangY,ZhangY.Stabilityoflargescalesystemswithnonlinearinfinitedelays[J].ChineseQuarterlyJournalofMathematics, 1990, 5(3): 100-101.

[6]胡何丽. 非线性不确定时变时滞中立系统的非脆弱控制[J]. 沈阳大学学报(自然科学版), 2013 (1): 39-44.

HuHL.Non-fragilecontrolfornonlinearuncertainneutralsystemswithtime-varyingdelays[J].JournalofShenyangUniversity(NaturalScienceEdition), 2013 (1): 39-44.

[7]杨芳, 刘万霞. 非线性二阶时滞微分方程的有界性[J]. 内蒙古财经学院学报(综合版), 2005(1): 1-2.

YangF,LiuWX.Boundednessofnonlineardifferentialequationswithtwoorderdelays[J].JournalofInnerMongoliaFinanceandEconomicsCollege, 2005(1): 1-2.

[8]WangM,ZhangSY,ChenB,etal.Directadaptiveneuralcontrolforstabilizationofnonlineartime-delaysystems[J].ScienceChinaInformationSciences, 2010, 53(4): 800-812.

[9]PhatVN,KhongthamY,RatchagitK.LMIapproachtoexponentialstabilityoflinearsystemswithintervaltime-varyingdelays[J].LinearAlgebraandItsApplications, 2012, 436(1): 243-251.

[10]JayawardhanaB,OuyangR,AndrieuV.StabilityofsystemswiththeDuhemhysteresisoperator:Thedissipativityapproach[J].Automatica, 2012, 48(10): 2657-2662.

[11]WangZH,DuML,ShiM.Stabilitytestoffractional-delaysystemsviaintegration[J].ScienceChinaPhysics,MechanicsandAstronomy, 2011, 54(10): 1839-1846.

[12]YangRM,WangYZ.Stabilityforaclassofnonlineartime-delaysystemsviaHamiltonianfunctionalmethod[J].ScienceChinaInformationSciences, 2012, 55(5): 1218-1228.

[13]JohnsonMA,ZumbrunK.Nonlinearstabilityofperiodictravelingwavesolutionsofsystemsofviscousconservationlawsinthegenericcase[J].JournalofDifferentialEquations, 2010, 249(5): 1213-1240.

责任编辑陈呈超

Unconditional Stability of Nonlinear Constant Large Scale Systems with Large Time Delay

HAN Yue-Qiao， GAO Cun-Chen

(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)

Abstract:In this paper, nonlinear constant large scale systems with large time delay are under consideration. Generally speaking, issues of large time delay systems have been rarely investigated yet because it is difficult to deal with the state term, which brings some difficulties to the dissussion of the problem. Motivated by the above discussion, the purpose in this work lies in overcoming the difficulties. By using the Lyapunov function decomposition method (that is the method of Lyapunov function of the scalar sum) and the equivalence method of differential equations and differential difference equations (that is decomposition equivalent method), a sufficient condition of unconditional stability is obtained. In addition, different from the previous research which takes attentions on the small time delay, this paper aims to investigate systems with large delay and find a way to keep the systems unconditionally stable, which proposes a new method for study on such problems. At last, a numerical example is presented to illustrate the effectiveness of the proposed approach. It is worth pointing out that the unconditional stability criterion of this paper would be extended to other systems such as nonlinear time varying systems with large time delay in the furture.

Key words:constant large scale systems；large time delay；nonlinearity；unconditional stability

DOI：10.16441/j.cnki.hdxb.20130343

中图法分类号：O211.6

文献标志码：A

文章编号：1672-5174(2016)03-134-07

作者简介：韩月乔(1991-)，女，博士生。E-mail:415778808@qq.com

收稿日期：2013-09-04；

修订日期：2015-12-10

*基金项目：国家自然科学基金项目(60974032)资助

引用格式：韩月乔， 高存臣. 具有大时滞的非线性定常大系统的无条件稳定性[J]. 中国海洋大学学报(自然科学版), 2016, 46(3): 134-140.

Supported by National Natural Science Foundation of China(60974032)