南海陆坡区约束流核型内孤立波观测研究*

于　博， 黄晓冬， 董济海， 赵　玮

(中国海洋大学物理海洋实验室， 山东 青岛 266100)



南海陆坡区约束流核型内孤立波观测研究*

于博， 黄晓冬**， 董济海， 赵玮

(中国海洋大学物理海洋实验室， 山东 青岛 266100)

摘要：本文基于南海陆坡区内孤立波的观测，对内孤立波的基本特征进行了研究，经分析得到其振幅为45m，最大水平流速可达1.6m·s(-1)，最大垂向流速为0.39m·s(-1)，传播速度为1.46m·s(-1)。将内孤立波经过时的流速、温盐特征进行了对比分析，结果表明,该内孤立波引起水质点的最大水平流速大于其传播速度，即u(max)>c，形成了约束流核; 在内孤立波核心处水体密度近乎一致，N2接近于0，理查德森数Ri<0.25，发生了剪切不稳定。基于内孤立波的振幅并结合背景场温盐剖面，对内孤立波引起的温盐场起伏进行反演，并对其动能、势能进行了估算。

关键词：内孤立波； 约束流核； 剪切不稳定； 破碎

YU Bo, HUANG Xiao-Dong, DONG Ji-Hai, et al. Observation of a trapped core internal solitary wave in South China Sea[J]. Periodical of Ocean University of China, 2016, 46(3)： 1-7.

在世界诸多海域内，大振幅内孤立波经常被观测到，其中南海是大振幅内孤立波频发的海域。南海内孤立波一般认为是由吕宋海峡较强潮流与复杂的山脊地形相互作用产生，其在向西传播过程中波形逐渐变陡、强度逐渐增大，卫星图像显示在120.5°E以东没有内孤立波出现，而在东沙岛附近有较多内孤立波出现[1]。在深水区，内孤立波的传播速度在3m·s-1左右[2-3]，最大水平流速可以超过2m·s-1[4]，其相速度大于最大水平流速，并且在深水区传播过程中相速度、水平流速变化较小。内孤立波向西传播经过陆坡区域时，由于水深变浅，其相速度迅速减小，但其水平流速保持相对稳定，使得一部分水质点的水平流速大于内孤立波相速度，达到了内孤立波破碎的条件，内孤立波会携带这部分水体随之运动，即在内孤立波内部形成了trapped core，即约束流核[5]。Lien等[6]在东沙岛附近观测到了具有这一特征的内孤立波，其相速度从2m·s-1减小到1.3m·s-1，而水质点的速度超过2m·s-1。

理论和模式结果表明内孤立波的破碎是由剪切不稳定或对流不稳定引起的[7]。在理查德森数Ri<0.25的区域内孤立波会发生剪切不稳定。Moum等[8]表明，剪切不稳定发生在上层水体内部和上下层水体的界面处。模式结果表明由于水深变浅，当内孤立波水质点的流速超过其相速度时会发生对流不稳定[9-10]。

对处于破碎过程中的内孤立波的直接观测很少，一方面是因为内孤立波破碎过程的具有间歇性，另一方面是因为需要高时空分辨率的全深度流速、密度场才能捕捉到引起内孤立波破碎的不稳定过程[11]。

鉴于处于破碎过程中的内孤立波现场观测较少，本文利用全深度流速和温盐剖面观测数据，对南海陆坡区的内孤立波进行了研究，对内孤立波流速、温盐场的特征进行了详细的分析。

1观测介绍

东方红2号科考船于2014年6月5日对同一个内孤立波进行了追踪观测。 内孤立波于14：25第一次传播经过科考船(见图1 (a)，117.43°E，21.27°N)，随后科考船对其进行追踪，于15:17经过内孤立波(见图1 (b)，117.40°E，21.34°N)，而后继续前进，在117.36°E，21.46°N停船等待内孤立波到达，内孤立波于16:53到达科考船所在位置(见图1 (c))，本文称之为观测点(即科考船与内孤立波第三次相遇的位置)，观测点水深为340m。在追踪过程中，利用船载75kHz ADCP观测内孤立波经过时的流速场，船载ADCP设置如下：采样间隔为1min，垂向共50个bin，每个bin的范围为16m，第一个bin与仪器的垂直间距为24.72m，因此可以观测到表层24.72m到海底的流速、后向散射强度数据；在停船对内孤立波进行观测的过程中同时下放SBE911plus CTD，获得海水温度、盐度等剖面，共进行7次下放，获得14个剖面数据，第1次下放深度为335m，后6次下放深度为200m。

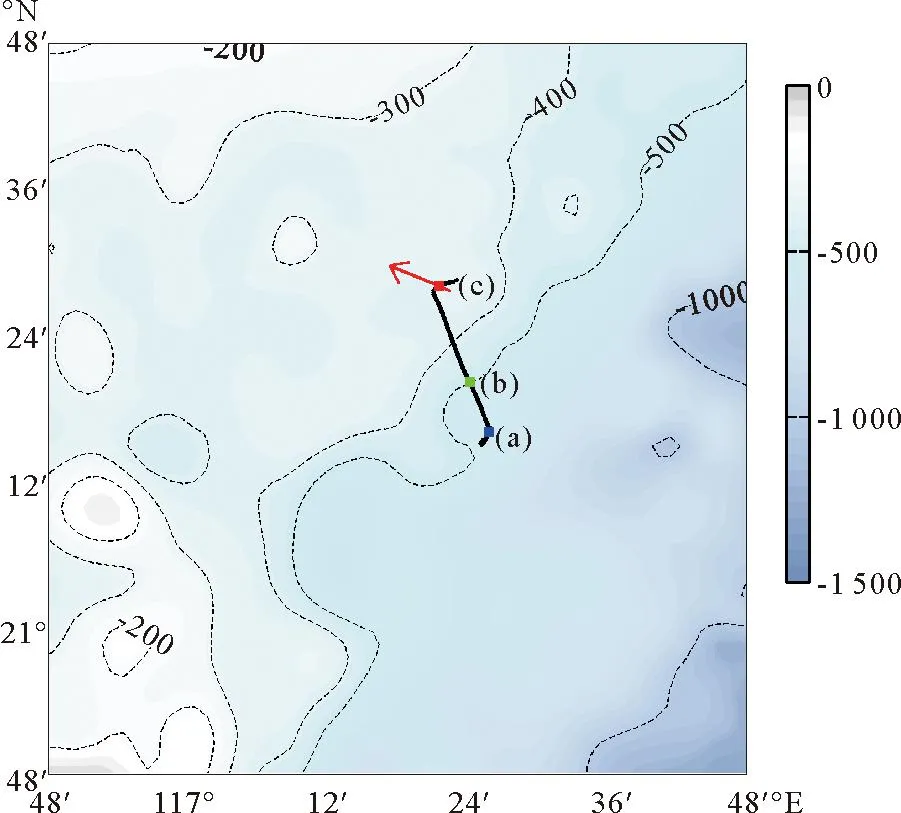
(图中西南是东沙岛。其中方块(a)、(b)、(c)表示前后3次与内孤立波相遇的位置，黑色实线表示科考船运动轨迹，红色箭头代表内孤立波的传播方向。South China Sea Southwest of the figure is Dongsha Island. The blue，green and red square is the first, second and third encountered point. The white curve labels the ship track.)

图1南海西北部地形图

Fig.1Topography of the north west

2内孤立波传播速度

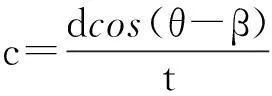
根据上式得到前2个相遇点间的传播速度c1=1.34m·s-1，传播方向θ1=281°；后2个相遇点间的传播速度c2=1.46m·s-1，传播方向θ2=293°。表明内孤立波主要向西传播。

根据KDV方程可以得到内孤立波的传播速度[12]：

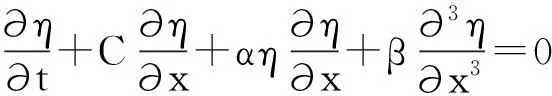
(1)

其中：η代表内孤立波的振幅；c0为线性相速度；α表示非线性系数；β是频散系数。结合SBE911plus CTD观测到的背景场温盐剖面的数据，通过(1)式可以得到内孤立波传播速度的理论值:

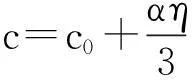
(2)

根据(2)式得到在观测点处内孤立波传播速度为1.50m·s-1。

传播速度的理论值和实测值相差不大，因此在观测点处该内孤立波的传播速度为c=1.46m·s-1，传播方向θ=293°。

3内孤立波特征

3.1 船载ADCP观测

内孤立波第3次经过时，船载ADCP观测到的后向散射强度、流速如图2所示，可以看出其为典型的第一模态下凹型内孤立波且表现为孤立波波包的形式，包含4个子波，其中头波振幅最大，流速最强，另外3个子波相对较弱。头波周期为16min，波长L=cT，为1.4km。

图2(a)为船载ADCP观测得到的后向散射强度数据,其中红色实线为内孤立波引起的后向散射强度最大起伏，其初始深度为104m。内孤立波的经过会引起等密度面的起伏，后向散射强度可以很好的反映等密度面的起伏状况，因此这里将后向散射强度的最大起伏定义为内孤立波振幅，则该内孤立波振幅为45m。

图2(b)是沿内孤立波传播方向(近似为东西方向，下文中称之为东西向)的水平流速，上层为较强的西向流动，下层为相对较弱的东向流动，但均比背景流大得多，为典型的第一模态下凹型内孤立波流速特征，最大西向流速为1.6m·s-1，出现在57m水深处。水平最大流速出现在海洋表面以下，而不是越接近表面流速越大，与理论结果不同，并且水平最大流速大于内孤立波传播速度，即umax>c(见图2(b)中白色曲线内的水体)，表示发生了对流不稳定，白色曲线内的水体会随着内孤立波一起传播，即约束流核[13]。

图2(c)为内孤立波垂向流速，波前为下降流会引起海面水体的幅聚，波后是上升流，会引起海面水体的幅散，卫星图像正是根据水体幅聚幅散对光线反射率的不同进而在海面上呈现出亮暗相间的条纹来观测内孤立波的。内孤立波引起的最大下降流速为0.39m·s-1，在122m深度处，最大上升流速也是0.39m·s-1，但位于106m水深处。可以看出内孤立波垂向流速在波前波后具有不对称的特征，正是由于这种特征使得内孤立波能够引起较强的垂向水体、物质输运。Dong等[14]研究了内孤立波垂向流速结构的不对称性，内孤立波经过之后使得水体升温达2.3℃，无机盐浓度升高了12.04μmol/L，叶绿素的含量升高了0.12μg/L，表明内孤立波对垂向水体、物质输运有着重要影响。

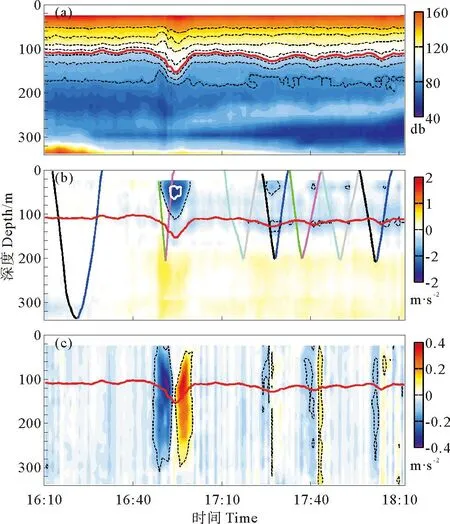
((a)后向散射强度数据，图中黑色虚线是80~140db等值线，间隔为10 db。(b)沿内孤立波传播方向的水平流速，黑色虚线为0.4m·s-1西向流速，白色实线表示内孤立波传播速度的大小。V字形颜色曲线为SBE911plus CTD下放回收的深度时间曲线。(c)垂向流速，图中黑色虚线分别代表0.08m·s-1上升、下降流速。图中红色实线均为后向散射强度起伏。(a) Acoustic echo density, the black dashed lines denote acoustic echo density from 80db to 140db, the contour interval is 10db. (b) Along-wave velocity, the black dashed lines indicate the along-wave velocity is 0.4 m·s-1, the thick white solid line indicate the phase speed of ISW, and the thick color lines in V shape denote time and depth of deployed SBE911plus CTD. (3) Vertical velocity, the black dashed lines denote the value of vertical velocity is 0.08m·s-1. The thick red solid line denotes the maximum vertical displacement of acoustic echo.)

图2船载ADCP观测结果

Fig.2Observation from shipboard ADCP

3.2 SBE911plus CTD剖面观测

SBE911plus CTD观测到的14个剖面的深度时间曲线如图2(b)所示。按时间依次将其命名为1~14号剖面。各个剖面的温度、Brunt-Väisälä频率平方即N2随深度的变化规律如图3所示。

前两个剖面的温度数据可作为背景场温度，表层海水最高温度为30℃，随深度增加逐渐降低，底层海水最低温度为11℃，混合层厚度约为35m，N2最大值出现在45m深度附近。从图2(b)第4个剖面接近内孤立波的核心区域，该剖面在40~60m层之间经过内孤立波约束流核的边缘，内孤立波经过时能够引起水体强烈的垂向运动，波前最大下降流速为0.39m·s-1，将水体向下输运，从温度曲线可以看出，混合层厚度由背景场的35m剧变到95m，加深了60m，温跃层深度也随之加深了60m。从N2曲线中可以看到N2最大值出现在105m处，在40~60m之间，即约束流核区域N2的数值接近0。第5个剖面的温度和N2曲线可以看出头波经过之后海洋的温度、层结特征迅速恢复到了背景场的情况。从后面几个剖面曲线可知该内孤立波较弱的3个子波对温度、层结等的影响很小。

3.3 内孤立波剖面特征

1号剖面数据采集时间点在内孤立波到达之前，可作为背景场数据，4号剖面数据是在内孤立波核心到达时采集的，将其作为内孤立波核心处的数据。5号剖面数据在内孤立波头波经过后采集，将其作为内孤立波过境后的水体数据。选取1、4和5号CTD剖面数据，对应时间内沿内孤立波传播方向、垂直于传播方向的水平流速时间平均值及内孤立波核心处垂向流速时间平均值对内孤立波特征进行详细分析。垂向剖面特征如下所示。

内孤立波头波经过后，20~40m深度处的水体温度下降，在35m处最大温度差为1.26℃(见图4(a)、(e))，但盐度并没有类似的现象(见图4(b))，该低温水团有可能是内孤立波携带输运过来的。与内孤立波经过前后水体密度层结相比，其核心处密度层结有很大不同，30~80m深度的水体密度近乎一致，N2接近于0(见图4(c)、(d))。

沿内孤立波传播方向，内孤立波前后水平流速比内孤立波核心处的水平流速要小的多(见图5(a))；对内孤立波核心处的水平流速而言，其西向流最大值为1.46m·s-1(因同样的原因其小于上文提到的最大西向流速)，而东向流速最大值为0.4m·s-1，前者是后者的3倍多，且西向流速在接近海洋表面的深度上有减小趋势。文献[11]表明这是由于在内孤立波核心处，水体因对流不稳定而发生翻转，这种翻转的影响可以直达海面，使内孤立波核心处的水平流速越接近海面越小。对垂直于内孤立波传播方向的水平流速而言(见图5(b))，内孤立波核心处的流速与其前后的流速相比相差不大，也说明了内孤立波主要是向西传播的。

垂向流速剖面是对内孤立波流核处的上升流与下降流分别取时间平均值得到的，因此其最大值比上文提到的内孤立波上升、下降流的最大值要小(见图5(c))，上升流与下降流最大值分别出现在105与121m处，且两者曲线并不对称。

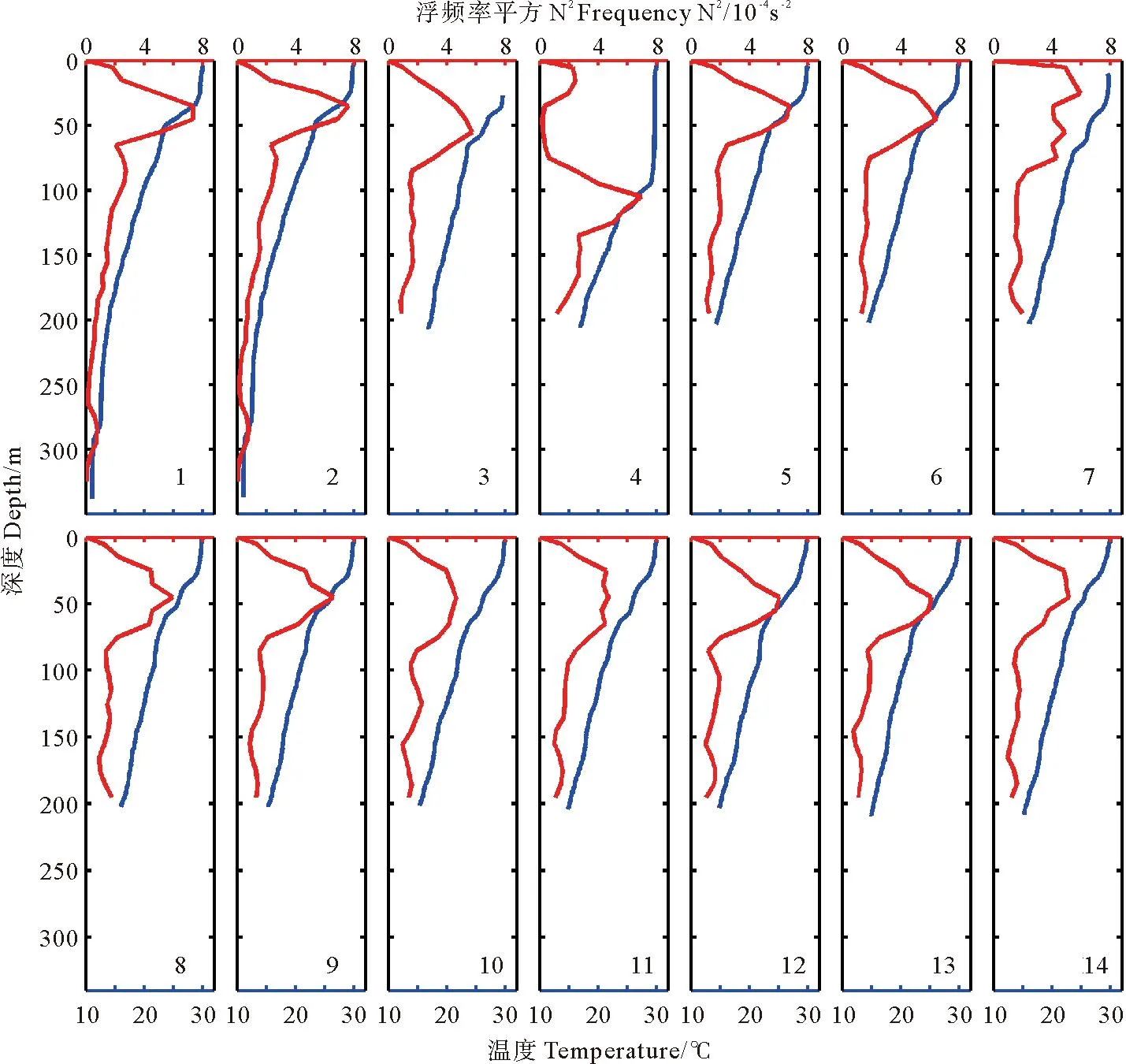
(其中蓝线、蓝色刻度值表示温度数据，红线、红色刻度值表示N2数据，图中右下角的数字表示剖面的序号。Blue lines denote temperature and red lines denoteN2.)

图3SBE911plus CTD观测的温度、Brunt-Väisälä频率平方的剖面图

Fig.3Temperature observed by SBE911plus CTD and calculated Brunt-Väisälä frequency

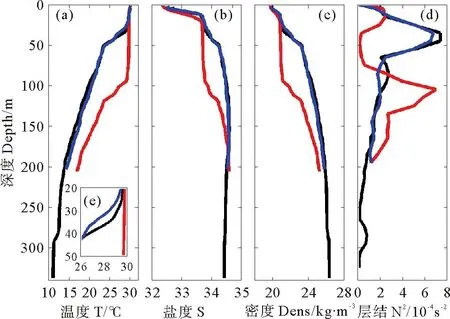
((e)是(a)图中20~50m结果的局部放大图。图中黑线表示1号剖面数据或1号剖面对应时间内的平均数据即背景场数据，红线表示4号剖面数据或其对应时间内的平均数据即内孤立波核心处的数据，蓝线表示5号剖面数据或其对应时间内的平均数据即头波过境后的数据。The inset (e) in (a) shows the temperature from upper 20~50m. The black lines denote the data from profile 1st, the red lines denote the data from profile 4th, and the blue lines denote the data from profile 5th.)

图4内孤立波经过前后温度(a)、盐度(b)、

密度(c)及层结(e)的变化

Fig.4Vertical profiles of (a) temperature,

(b) salinity, (c) potential density and (4) N2

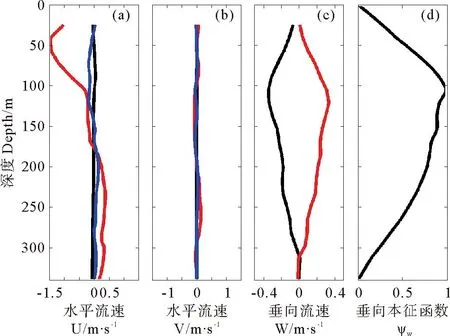
((a)沿内孤立波传播方向的水平流速。(b)垂直于内孤立波传播方向的水平流速。(c)内孤立波核心处的垂向流速(时间平均)。(d)垂向本征函数。对于图(a)、(b)来说为黑线表示1号剖面数据或1号剖面对应时间内的平均数据即背景场数据，红线表示4号剖面数据或其对应时间内的平均数据即内孤立波核心处的数据，蓝线表示5号剖面数据或其对应时间内的平均数据即头波过境后的数据。(c)中的黑线、红线分别表示内孤立波核心处下降流与上升流的时间平均值。Vertical profiles of (a) along-wave velocity, (b) cross-wave velocity, (c) vertical velocity,(d) linear eigen-modal. The black lines in (a)、(b) denote the data from profile 1st, the red lines denote the data from profile 4th, and the blue lines denote the data from profile 5th. The black and red line in (c) denote time averaged downwelling and upwelling, respectively.)

图5内孤立波经过前后流速变化特征

Fig.5The variation of velocity when the ISW passed by

根据内波垂向本征方程，结合1号剖面温盐数据可以得到其垂向本征函数(见图5(d))，结果表明，内孤立波最大振幅出现在105m处，而本文根据后向散射强度起伏得到的内孤立波最大振幅在104m处，两者一致，表明后向散射强度能很好地反应等密度面的起伏。

((a)沿内孤立波传播方向水平流速的垂向剪切。(b)垂直于内孤立波传播方向水平流速的垂向剪切。(c)沿内孤立波传播方向的水平流速与垂直于内孤立波传播方向垂向剪切的平方和。(d)理查德森数。对于图(a)~(d)来说黑线表示1号剖面数据或1号剖面对应时间内的平均数据即背景场数据，红线表示4号剖面数据或其对应时间内的平均数据即内孤立波核心处的数据，蓝线表示5号剖面数据或其对应时间内的平均数据即头波过境后的数据。(d)中的黑色虚线表示Ri=0.25。Vertical profiles of (a) vertical shear of along-wave velocity, (b) vertical shear of cross-wave velocity, (c) total vertical squared of horizontal velocity, (d) Richardson number. The black lines in (a)~(d) denote the data from profile 1st, the red lines denote the data from profile 4th, and the blue lines denote the data from profile 5th. The black dashed line in (d) denote the value of Ri which is 0.25.)

图6流速垂向剪切及理查德森数

Fig.6The feature of vertical shear of velocity and

Richardson number

对沿内孤立波传播方向流速的垂向剪切来说(见图6(a))，内孤立波核心处的最大峰值出现在95m深度处，在175m深度上也有一个较小的峰值，而内孤立波经过前后水平流速的垂向剪切没有明显的峰值。对垂直于内孤立波传播方向的水平流速的垂向剪切而言(见图4(b))，均没有明显峰值出现。

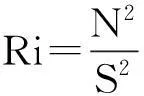
4内孤立波的能量

4.1 温度场的构建

对内孤立波能量进行计算，首先要获取内孤立波经过时的温度场与盐度场，进而计算出内孤立波的密度场。在观测中只有14个温度剖面，因而需要对温度场进行重新构建。方法如下：

(1)背景场：采用1、2号剖面的温度平均值作为背景场温度，记为T(z)。

(2)内孤立波起伏：通过后向散射强度提取内孤立波振幅及其所在深度，记为，结合垂向本征函数，计算出内孤立波在各深度的起伏：

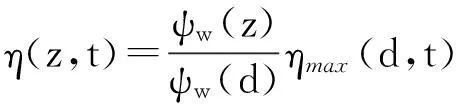
(3)

(3)温度场模拟：内孤立波经过时，等温度面将随之起伏，即可得到各个深度的扰动温度：

T′(z,t)=T(z-η(z,t))。

(4)

模拟得到的温度场如图7(a)所示，选择1、4、5号剖面的实测值与其对应时间、深度位置上的模拟值作对比(见图7(b)~(d))，从对比图中可以看出内孤立波

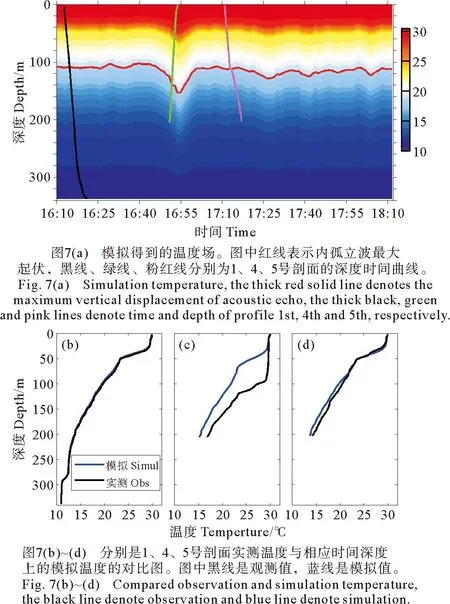
图7　内孤立波温度场反演

到达之前模拟值与实测值基本一致(见图7(b))，对于内孤立波头波经过之后，模拟值与实测值吻合较好(见图7(c))，只在100m以下出现较小的误差，但对于内孤立波核心处，在内孤立波起伏较大的位置模拟值与实测值相差较大，这可能是 由于在内孤立波核心处存在对流不稳定。

通过同样的方法可以得到盐度场数据，从而计算出密度场。

4.2 能量的计算

对于二维非静力近似下的内孤立波，其动能KE的表达式为[15]，

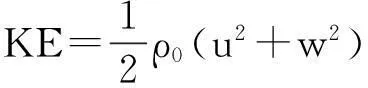
(5)

其中：ρ0=1024；u是沿内孤立波传播方向的水平流速；w是垂向流速。对于最上层缺测的流速数据，结合约束流核型内孤立波的特点，本文认为海表面流速是0，进而利用ADCP观测最上层的流速数据进行线性插值得到缺测深度的流速。

Kang和Fringer[16]讨论了内孤立波有效势能的表达式，认为有效势能APE最优的表达式为：

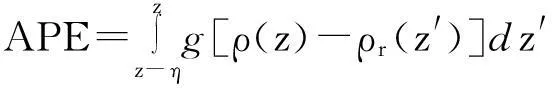
(6)

其中:g为重力常数;η是等密度面的起伏;ρr是背景场密度；ρ是现场密度。

内孤立波的能量E=KE+APE。根据上面动能和势能的表达式计算得到该内孤立波的动能和势能分别是94和53 MJ·m-1，动能接近势能的两倍，这一方面是由于内孤立波在破碎的过程中动能与势能之间存在着转化关系；另一方面是由于在温度场的构建过程中，在内孤立波起伏较大的位置温度的模拟值与实测值相差较大，没能充分反映内孤立波的起伏对温度的影响，使计算得到的势能较小。

5结论与展望

本文基于船载ADCP和SBE911plus CTD剖面的观测，对南海西北部陆坡区典型内孤立波波包个例进行了分析，研究了其流速场和温盐场的特征，结果如下：

(1)该内孤立波波包共包含4个子波，其中头波振幅最大、流速最强，其传播速度c=1.46m·s-1，波长和振幅分别为1.4km和45m，沿内孤立波方向的最大水平流速为1.6m·s-1，最大垂向流速为0.39m·s-1，其余3个子波的流速、振幅逐渐减小。

(2)对内孤立波流速场进行研究，发现在该内孤立波核心处水质点水平流速大于其传播速度，即umax>c，表明在核心处存在对流不稳定，满足内孤立波破碎的条件；在内孤立波核心处尤其是约束流核区域上下层的密度趋于一致，N2接近于0。在内孤立波核心处上100m层中，Ri<0.25，发生了剪切不稳定。

(3) 根据CTD剖面数据以及内孤立波垂向本征函数，结合其振幅特征，对内孤立波引起的温盐场起伏进行了模拟，重新构建了内孤立波到达时的温度、盐度场，并对内孤立波的能量进行了估算，该内孤立波的动能为94 MJ·m-1，势能为53 MJ·m-1，动能接近势能的2倍，其总能量为147 MJ·m-1。

本文对南海陆坡区约束流核型内孤立波的基本特征进行了分析，下一步工作需要获取全深度、高时空分辨率的潜标观测资料，并对其进行进一步的研究。

参考文献：

[1]Zhao Z, Klemas V V, Zheng Q, et al. Remote sensing evidence for baroclinic tide origin of internal solitary waves in the northeastern South China Sea [J]. Geophys Res Lett, 2004, 31(6): 177-182.

[2]方文东, 施平, 龙小敏, 等. 南海北部孤立内波的现场观测 [J]. 科学通报, 2005, 50(13)： 1400-1404.

Fang W, Shi P, Long X, et al. Situ observation of internal solitary waves in the Northern South China Sea [J]. Chinese Science Bulletin, 2005, 50(13): 1400-1404.

[3]Alford M H, Lien R C, Simmons H,et al. Speed and evolution of nonlinear internal waves transiting the South China Sea [J]. J Phys Oceanogr, 2010, 40(6): 1338-1355.

[4]蔡树群, 甘子钧, 龙小敏. 南海北部孤立子内波的一些特征和演变 [J]. 科学通报, 2001, 46(15): 6.

Cai S, Gan Z, Long X. Features and evolution of internal solitary waves in Northern South China Sea [J]. Chinese Science Bulletin, 2001, 46(15): 6.

[5]Lamb. Shoaling solitary internal waves: On a criterion for the formation of waves with trapped cores [J]. Fluid Mech, 2003, 478: 81-100.

[6]Lien E A, D’ Asaro F, Henyey， Chang M H, et al. Trapped core formation within a shoaling nonlinear internal wave [J]. J Phys Oceanogr, 2012, 42: 511-525.

[7]Lamb, Farmer D. Instability in an internal solitary-like wave on the Oregon Shelf [J]. J Phys Oceanogr, 2011, 41: 67-87.

[8]Moum J N, Farmer D M, Smyth W D, et al. Vagle. Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf [J]. J Phys Oceanogr, 2003, 33: 2093-2112.

[9]Vlasenko V, and Hutter I . Numerical experiments on the breaking of solitary internal waves over a slope-shelf topography [J]. J Phys Oceanogr, 2002, 32: 1779-1793.

[10]Helfrich， White B L . A model for large-amplitude internal solitary waves with trapped core [J]. Nonlinear Processes Geophys, 2010, 17: 303-318.

[11]Lien F Henyey, B Ma, Chang M H, et al. Trapped core formation within a shoaling nonlinear internal wave [J]. J Phys Oceanogr, 2014, 44: 1095-1115.

[12]Alford M H, MacKinnon J A, Nash J D . Energy flux and dissipation in Luzon Strait: Two tales of two ridges[J]. Journal of Physical Oceanography, 2011, 41(11): 2211-2222.

[13]Lamb K G. Particle transport by nonbreaking, solitary internal waves[J]. Journal of Geophysical Research: Oceans (1978-2012), 1997,102(C8): 18641-18660.

[14]Dong J, Zhao W, Chen H, et al. Asymmetry of internal waves and its effects on the ecological environment observed in the northern South China Sea [J]. Deep Sea Research Part I: Oceanographic Research Papers, 2015, 98: 94-101.

[15]Moum J N, Klymak, J M, Nash J D, et al. Energy transport by nonlinear internal waves[J]. Journal of Physical Oceanography, 2007, 37(7): 1968-1988.

[16]Kang D, & Fringer O. On the calculation of available potential energy in internal wave fields[J]. Journal of Physical Oceanography, 2010, 40(11): 2539-2545.

责任编辑庞旻

Observation of A Trapped Core Internal Solitary Wave in South China Sea

YU Bo, HUANG Xiao-Dong, DONG Ji-Hai, ZHAO Wei

(The Lab of Physical Oceanography， Ocean University of China, Qingdao 266100, China)

Abstract:Based on the situ observation of internal solitary wave (ISW) in continental shelf of the northern south China Sea, the characteristic parameters of the ISW was calculated, the amplitude of ISW was 45m, the maximum along-wave velocity was 1.6m·s(-1), and the maximum vertical velocity was 0.39m·s(-1). The velocity and temperature profiles of the ISW were analyzed, it indicated that the maximum along-wave velocity exceeded the propagation speed of ISW, it reached the convective breaking limit and trapped core formed. In the core of ISW, the calculated Richardson number Ri<0.25, shear instability occurred. The kinetic energy and available potential energy were estimated based on the simulated temperature and salinity field.

Key words:internal solitary wave; trapped core; shear instability; wave breaking

DOI：10.16441/j.cnki.hdxb.20150108

中图法分类号：P731.24

文献标志码：A

文章编号：1672-5174(2016)03-001-07

作者简介：于博(1991-)，男，硕士生。E-mail：yubo_ouc@163.com**通讯作者：E-mail： xhuang@ouc.edu.cn

收稿日期：2015-03-17；

修订日期：2015-05-06

*基金项目：国家重点基础研究发展计划项目(2014CB745003 );国家高技术研究发展计划项目(2013AA09A502);国家自然科学基金项目(41176008，41176010) 资助

引用格式：于博， 黄晓冬， 董济海， 等. 南海陆坡区约束流核型内孤立波观测研究[J]. 中国海洋大学学报(自然科学版)， 2016, 46(3): 1-7.

Supported by National Basic Research Program of China (2014CB745003); National Nigh Technology Research and Development Program of China (2013AA09A502); National Natural Science Foundation of China(41176008，41176010)