自变量核心法在函数关系问题中的运用

李文浩

【摘要】在函数关系中，其概念与性质的运用均应以自变量为导向，即自变量核心法，有利于加深对函数关系的理解。本文应用4个示例对该解题方法进行了验证和说明。示例表明，自变量核心法可有效扩展学生在解决函数关系问题的思维空间，使诸多问题的解题方法更为简洁。

【关键词】函数关系 自变量 双元变量

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2016）03-0158-02

“自变量核心法”，是指在函数关系中，所有概念与性质在理解与运用时均应以自变量为导向。函数关系是由自变量与因变量变化关系而引发。所以，“自变量”无论是在时间上还是在空间上，都主导了函数问题的理解与应用，成为所有概念与性质共同遵循的准则。在某一关系式中，给定谁的范围或隐含条件，可尝试设定谁为自变量；在自变量隐晦不清的变化关系中，可尝试观察并抽象自变量来使得问题转化为明确的函数关系。举例说明。

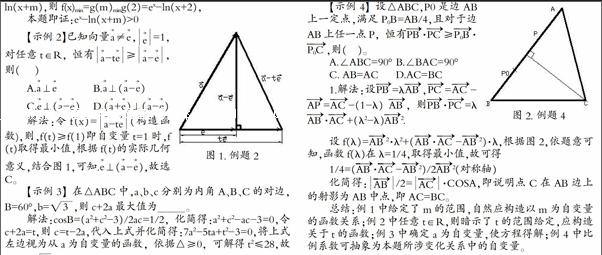
总结：例1中给定了m的范围，自然应构造以m为自变量的函数关系；例2中任意t∈R，则暗示了t的范围给定，应构造关于t的函数；例3中确定a为自变量，使方程得解；例4中比例系数可抽象为本题所涉变化关系中的自变量。