空间相机常用金属材料表面的BRDF特性
2016-04-19关洪宇刘巨于善猛关奉伟
关洪宇,刘巨,于善猛,关奉伟
(中国科学院 长春光学精密机械与物理研究所,吉林长春 130033)
空间相机常用金属材料表面的BRDF特性
关洪宇,刘巨*,于善猛,关奉伟
(中国科学院 长春光学精密机械与物理研究所,吉林长春130033)
摘要:为保证空间相机热设计中表面辐射换热计算准确可靠,基于两种金属材料的光学常数,结合Monte Carlo射线跟踪法应用几何光学近似对其粗糙表面的双向反射分布函数(BRDF)进行了研究。分析了不同入射光波长、不同入射角度及不同表面粗糙度对金属铝和钛材料粗糙表面的BRDF的影响。结果表明,金属铝和钛材料粗糙表面的BRDF分布具有明显的镜反射特征,入射平面内的BRDF峰值随入射光波长增加而增大,在本文研究的波长范围内,钛表面的BRDF随入射光波长增大的增幅最高达到41.0%,远高于铝表面的8.7%。当表面粗糙度较大时,光子在粗糙表面内会经历多次散射,粗糙表面内多次散射光子数比例随着表面粗糙度的增大而增加,并且随着入射角度的增大具有增加的趋势。
关键词:表面辐射;粗糙表面;几何光学近似;双向反射分布函数
1引言
空间相机对工作环境温度的变化非常敏感,由热引起的光机结构误差会导致相机的视轴漂移和光学系统的波前畸变,严重破坏成像质量。为保证空间相机所需的工作温度水平,要求相机热设计准确可靠。表面辐射换热是空间相机内部及与环境换热的主要形式之一,相机材料表面辐射特性数据对于热设计的准确性非常重要。固体材料的表面辐射特性与物质种类、光照波长、入射角度、表面温度及表面状况等多种因素有关[1-2],针对某一特定条件下材料表面辐射特性数据往往不易获得。Modest[3]指出表面辐射特性诸如发射率、吸收率、反射率以及透射率等是求解辐射传递问题的必要条件,这些参数需要通过实验方法求得,仅对于光滑的理想表面的辐射特性可以通过理论计算获得。Renhorn[4]建立了粗糙表面BRDF模型,在确定粗糙表面的表面参数后能在一定范围内较准确的描述BRDF数据。Fu[5]对随机粗糙表面的电磁波散射特性进行了研究,指出在忽略波的干涉和极化效应时,几何光学近似法较需求解麦克斯韦方程组的有限时域差分法(FDTD)具有更高的计算效率,是计算的首选。Chen等[6]使用严格耦合波算法(RCWA)对在晶片快速热处理过程中吸收的光谱能量分布和晶片的辐射特性进行了研究分析。黄志锋和周怀春等[7]运用有限时域差分法计算了一维栅格结构的辐射特性,对粗糙硅的表面辐射特性进行了分析研究。帅永、刘彬等[8]通过实验方法对微粗糙硬铝表面的辐射特性进行测量,实验结果显示在长波入射、大角度入射时可观测到后向反射增强效应。国内外针对表面辐射特性提出了多种计算和测量方法,主要包括有限时域差分、严格耦合波算法、几何光学近似法以及实验测量方法等。FDTD 方法是在时域内对麦克斯韦方程组进行求解,已经广泛应用在不同的领域。对于周期性结构体,RCWA方法能够得到较精确的结果。几何光学近似方法只在一定的范围内适用,具有较高的计算效率。
双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)能够准确表征出表面反射能量的空间分布特征,是求表面反射特性的最基本的参数,对于非透明固体材料表面,通过BRDF即可求得相应条件下的表面吸收率和反射率等表面辐射特性数据。目前基于材料光学常数对其粗糙表面的双向反射分布函数的研究还鲜有报道。本文应用Monte Carlo射线追踪法基于几何光学近似对空间相机中常用的两种金属材料铝和钛粗糙表面的BRDF进行数值模拟,分析了不同入射光波长、不同入射角度以及不同表面粗糙度对金属铝和钛粗糙表面BRDF的影响。
2空间相机常用金属材料的光学常数
由文献[9-11]查得金属铝和钛的不同入射光波长λ下的光学常数如表1所示,其中n为折射率,k为吸收指数。
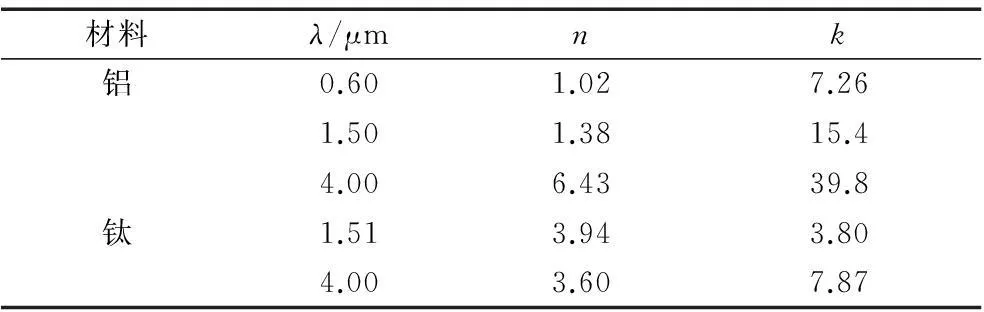
Tab.1 Optical constants of aluminum and titanium
结合材料光学常数通过菲涅尔方程可以计算得到光滑金属铝板和钛板的反射率随入射角度变化曲线,图1 和图2分别是不同入射光波长下的光滑铝板和钛板的半球积分反射率随入射角度变化曲线(其中θ为天顶角,下标i表示入射方向,下标r表示反射方向,下同)。由图1和图2可以看出,对于光滑铝板和钛板,随着入射光波长增大,不同入射角度下的半球积分反射率随之增加,当θi小于60°时,不同入射光波长下光滑铝板和钛板的半球积分反射率基本保持不变,当θi大于60°时,光滑铝板和钛板的半球积分反射率先减小后增大,随波长增大而增加的趋势放缓。

Fig.1Reflectivity of smooth aluminum plate on different wavelength of incident light

Fig.2Reflectivity of smooth titanium plate on different wavelength of incident light
3空间相机常用金属粗糙表面的BRDF
为对空间相机常用金属粗糙表面的BRDF分布特性进行数值模拟,应用高斯随机粗糙表面模型,将测得的光学常数赋到粗糙表面几何模型中,之后通过基于Monte Carlo射线跟踪法获得不同粗糙表面的BRDF,并对其分布特性进行分析。
二维随机粗糙表面的几何形貌可表示为平面坐标的函数为z=ζ(x,y),表面高度随机分布的统计特性由高度概率分布函数p=(ζ(x,y))和自相关函数C(τ)两个分布函数确定。本文应用高斯随机粗糙表面模型,高斯高度概率分布函数及自相关函数可分别表示,如公式(1)、(2)所示[12]。
(1)
(2)
其中ζ是表面高度变量,σ是均方根高度,τ是相关长度,r1、r2是沿表面两个不同的点。
对公式(2)进行傅里叶变换,可以得到功率谱密度函数,
(3)
其中k表示在空间频率域的变量。
根据以上数学模型,可以构建不同粗糙度的二维随机粗糙表面模型。
建立基于Monte Carlo方法的随机粗糙表面BRDF计算模型如图3所示,将通过数学模型得到的不同粗糙度的二维随机粗糙表面置于BRDF计算模型中心,在其上建立半球面作为光子经随机粗糙表面反射后的光子探测器,通过改变面光源与粗糙表面相对位置模拟光子的不同角度入射,模拟过程中面光源发射的总光子数为106,通过探测器表面不同位置上探测到的反射光子数可计算得到当前随机粗糙表面在2π空间下不同反射位置的BRDF。应用这一计算模型,对空间相机常用金属粗糙表面的BRDF分布特性进行数值模拟,分析不同入射光波长、不同表面粗糙度对金属材料表面BRDF的影响。
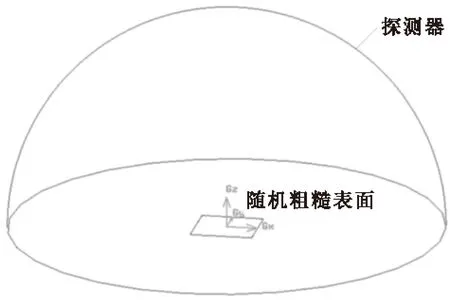
Fig.3BRDF computing model of random rough surfaces
3.1不同入射光波长下常用金属粗糙表面的BRDF
构建随机粗糙表面模型,令σ=0.020 mm,τ=0.030 mm。选取表1中三种对应金属铝材料的入射光波长,对粗糙铝板表面的BRDF特性进行了模拟,不同入射角度下粗糙铝板表面入射平面内的BRDF·cosθr随反射天顶角变化曲线如图4所示。
从图4可以看出,不同入射光波长下的粗糙铝板入射平面内的BRDF·cosθr在其镜反射方向出现峰值,表现出明显的镜反射特征,随着入射角度的增加,镜反射方向的峰值逐渐增大,说明镜反射特性随入射角度增大而增强,占反射能量分布的主要部分。在同一入射角度下,随着波长的增加,入射平面内镜反射方向的BRDF·cosθr峰值增大,这是由于对于波长较大的入射光,粗糙铝板更近似于光滑表面,并且从图1中可以看出,光滑铝板的半球积分反射率随波长的增加而增大。随着入射角度的增大,BRDF·cosθr峰值随波长增加而增大的幅度有所增大,在所选波长范围内,增大幅度范围为6.1%~8.7%。
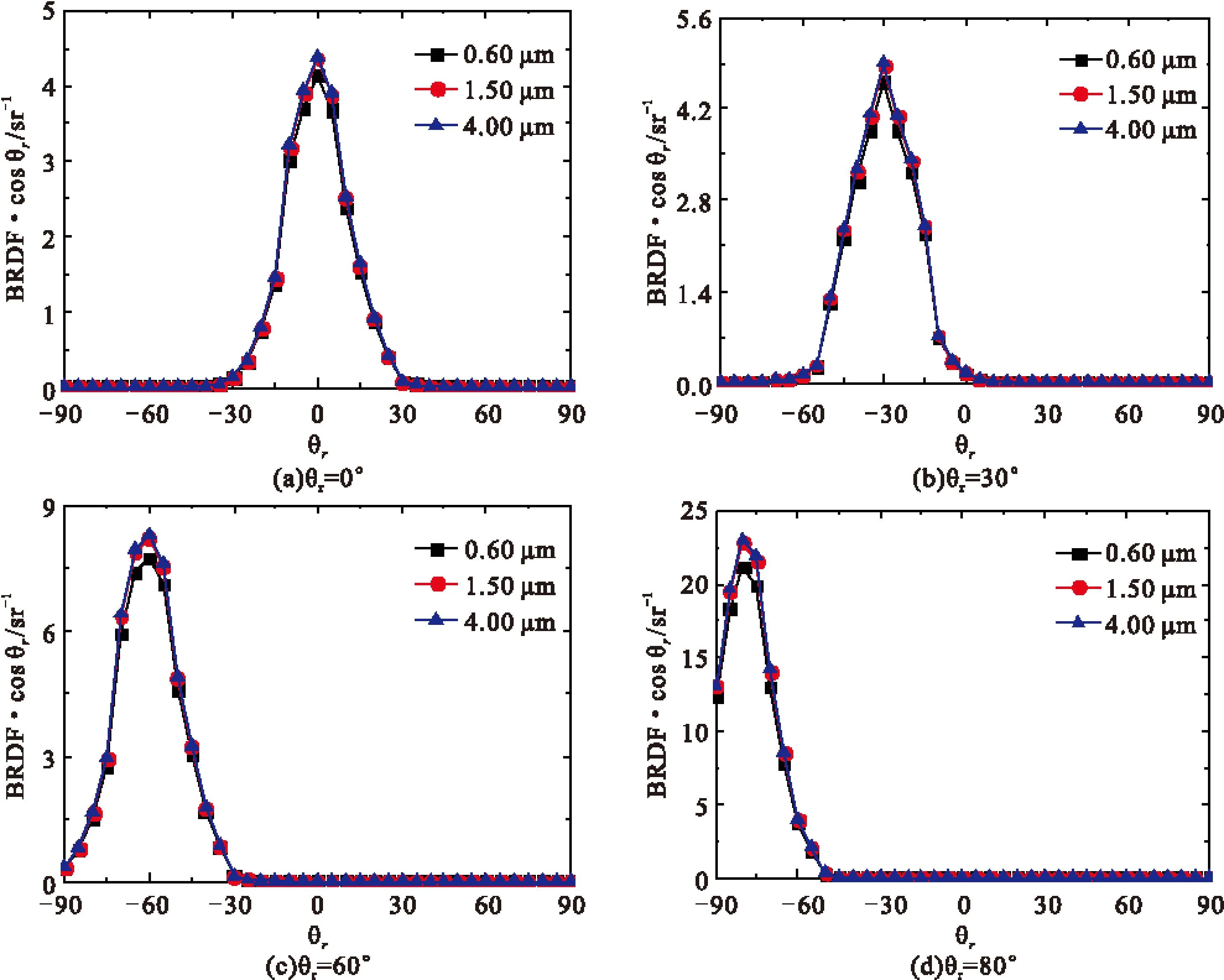
Fig.4 BRDF·cosθr of rough aluminum plate at different incident angles
选取表1中对应金属钛的两种入射光波长,对粗糙钛板表面的BRDF特性进行模拟,不同入射光波长下粗糙钛板表面入射平面内的BRDF·cosθr随反射天顶角变化曲线如图5所示。从图5中可以看出,不同入射角度下粗糙钛板表面入射平面内的BRDF·cosθr变化规律与粗糙铝板相同,即都具有明显的镜反射特征,镜反射方向的BRDF·cosθr峰值随入射角度增加而增大,随着入射光波长的增大, BRDF·cosθr峰值增加,增大的幅度范围为28.1%~41.0%。

Fig.5 BRDF·cosθr of rough titanium plate on different wavelength of incident light
3.2不同表面粗糙度下常用金属粗糙表面的BRDF
构建三种不同粗糙度的随机粗糙表面模型,对不同入射角度下粗糙铝板表面的BRDF特性进行模拟,计算过程中选取入射光波长0.60 μm。各随机粗糙表面参数如表2所示,不同表面粗糙度下粗糙铝板入射平面内的BRDF·cosθr随反射天顶角变化曲线如图6所示。
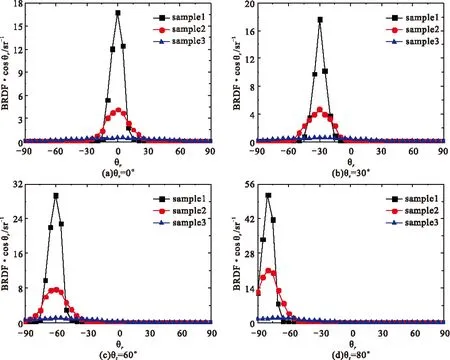
Fig.6 BRDF·cosθr of rough aluminum plate with different surface roughness
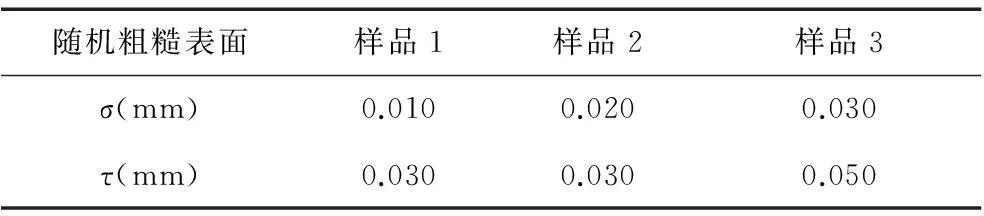
随机粗糙表面样品1样品2样品3σ(mm)0.0100.0200.030τ(mm)0.0300.0300.050
从图6中可以看出,不同表面粗糙度下粗糙铝板表面的BRDF·cosθr在镜反射方向附近出现峰值,随着表面粗糙度的增大,镜反射方向附近BRDF·cosθr峰值由陡峭逐渐趋于平缓,说明随着粗糙度的增大,漫反射占反射能量分布的比重增加,镜反射特性减弱,这是由于当表面粗糙度较小时,多数光子被直接反射到镜反射方向及其附近区域,镜反射特性较强,当粗糙度增大时,光子在粗糙表面内会经历多次散射,导致镜反射特性减弱,漫反射特性增强。不同表面粗糙度下粗糙铝板表面内多次散射光子数比例如表3 所示。

Tab.3 Ratio of multiple scattering photons in rough aluminum surface
从表3可以看出,同一入射角度下,随着表面粗糙度的增大,粗糙铝板表面内多次散射光子数比例增加,当表面粗糙度相同时,多次散射光子数比例随入射角度增大有增加的趋势。
图7给出了入射角度为30°时,不同表面粗糙度的粗糙铝板表面BRDF·cosθr极坐标分布图,从图7中也可以看出,反射能量主要分布在镜反射方向附近区域,随着表面粗糙度的增大,漫反射占反射能量分布的主要部分,镜反射性减弱,镜反射方向的BRDF·cosθr峰值减小。

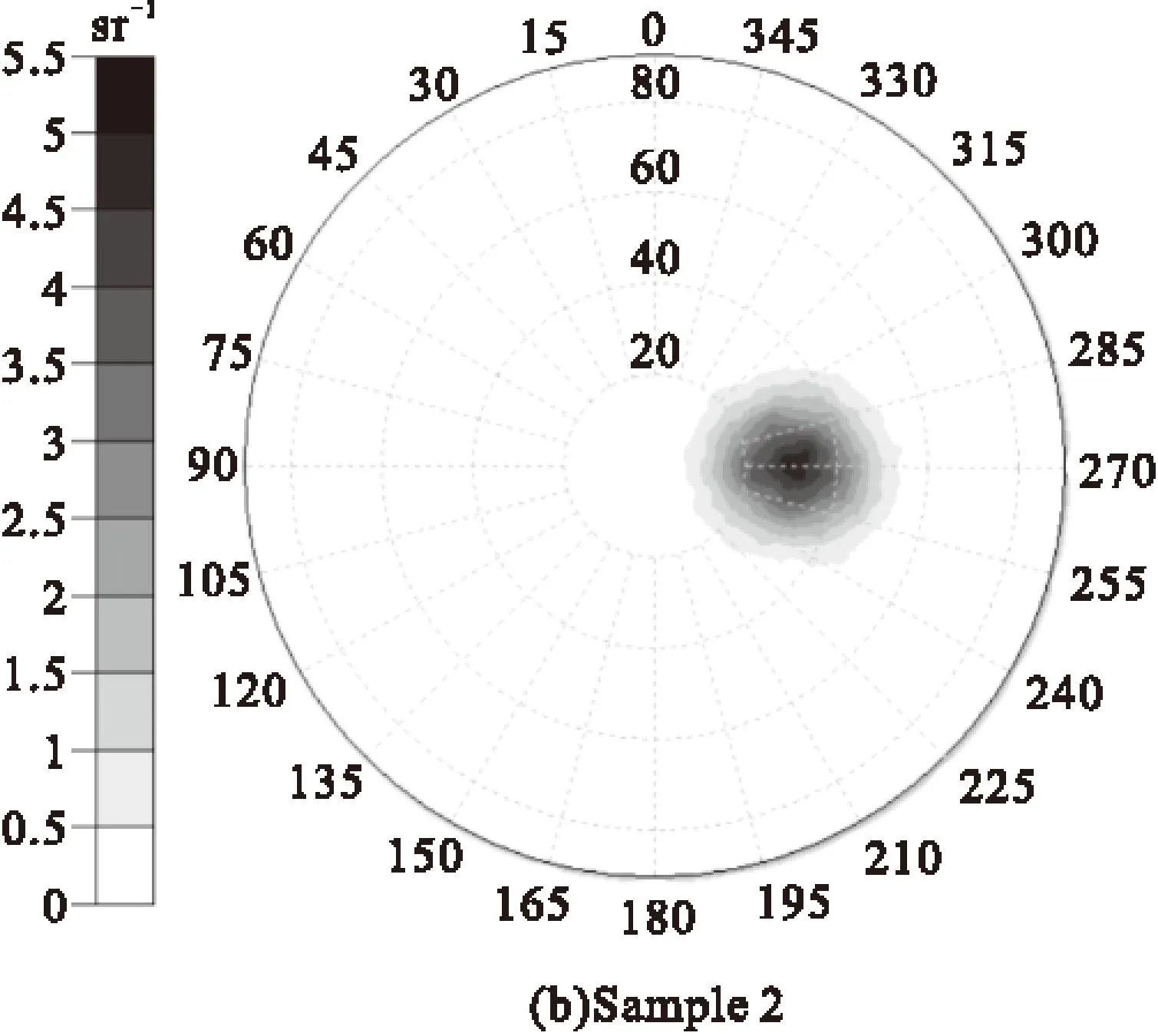

Fig.7Distribution of BRDF·cosθrof rough aluminum surface in polar coordinates
3.3随机粗糙钛板表面的BRDF实验测量
对随机粗糙钛板表面的BRDF使用哈尔滨工业大学双向反射分布函数测量实验台进行实验测量,BRDF实验测量原理及数据采集处理可参考文献[14]。实验过程中使用的光源波长λ是1550 nm,粗糙钛板表面σ=0.020 mm,分别测量了入射角为30°和60°下粗糙钛板表面的BRDF。图8是不同入射角度下随机粗糙钛板表面二分之一半球空间的BRDF分布,其中周向坐标表示方位角φ,径向坐标表示天顶角θ。图9是入射平面内粗糙钛板表面BRDF·cosθr随反射天顶角变化曲线。将图8和图9与图5进行比较可以看出,在λ=1500 nm条件下,随机粗糙钛板表面的BRDF实验测量结果与通过Monte Carlo方法模拟计算得到的结果具有相同的变化特征,即都具有明显的镜反射特性,在镜反射方向附近出现峰值,并且随着入射角度增大峰值增大。入射角θi=30°时,实验测量与模拟计算的BRDF·cosθr峰值相差33.4%;θi=60°时,实验测量与模拟计算的BRDF·cosθr峰值相差24.8%,实验测量的误差主要来自测量仪器本身误差以及测量环境条件的影响。
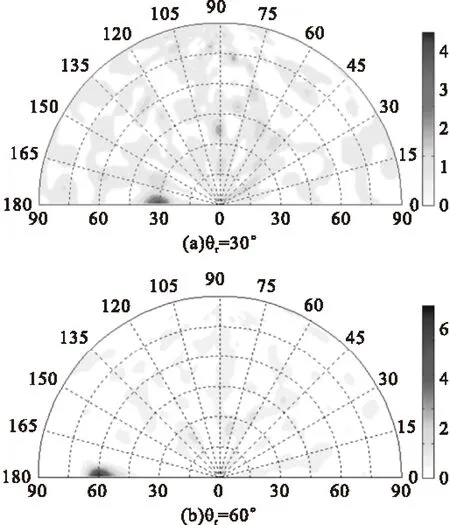
Fig.8BRDF of random rough titanium plate at different incident angles
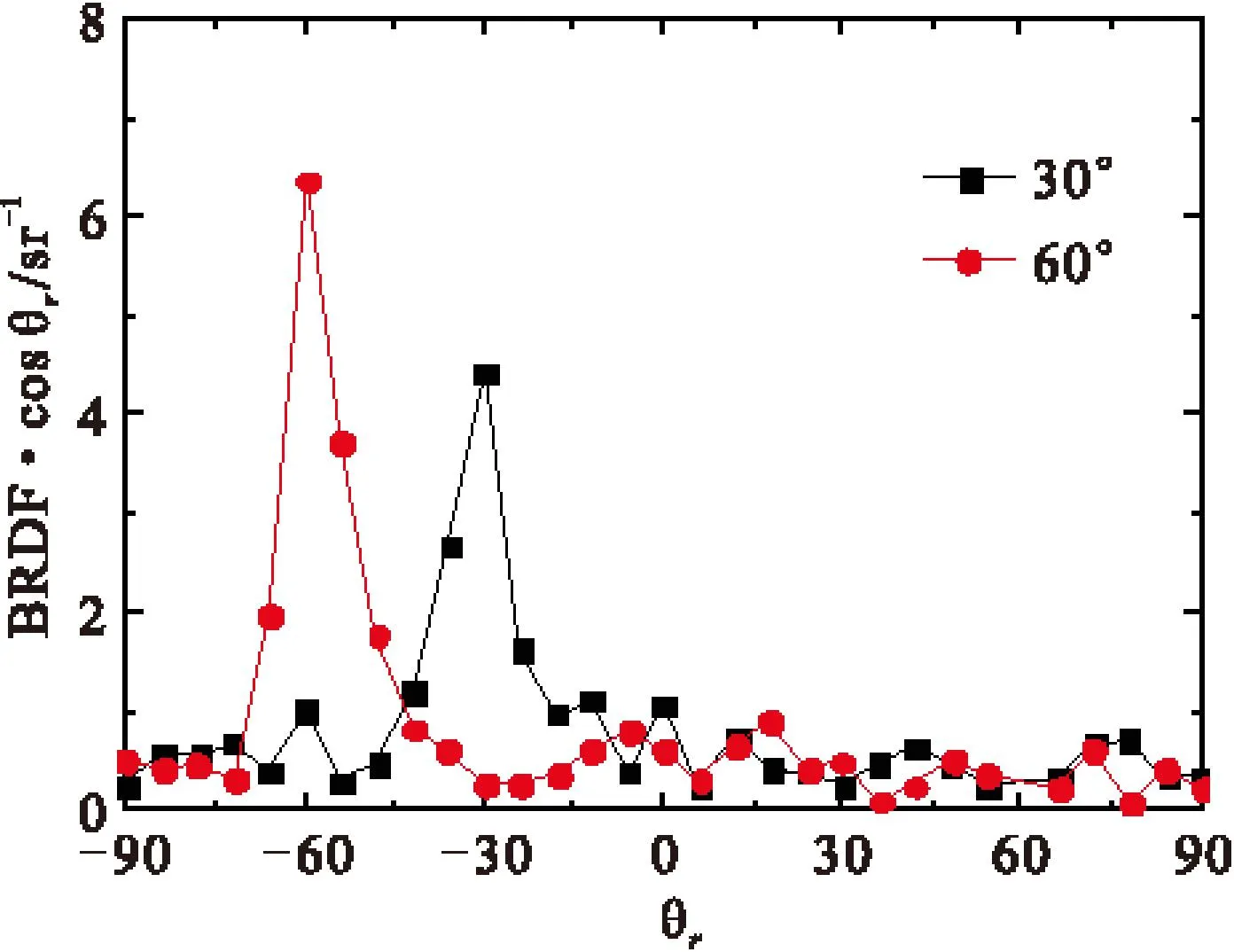
Fig.9BRDF·cosθrof random rough titanium plate in the incident plane
4结论
本文通过Monte Carlo射线跟踪法对空间相机常用金属材料粗糙表面的BRDF特性进行了数值模拟,分析了不同入射光波长、不同入射角度以及不同表面粗糙度对金属铝和钛材料表面的BRDF的影响。结果表明,粗糙铝板和粗糙钛板表面的BRDF分布具有明显的镜反射特征,镜反射方向附近BRDF峰值随入射角度的增大而增大。随着入射光波长的增加,粗糙铝板和钛板表面的BRDF峰值增大,但粗糙铝板的增幅不大,不超过8.7%,粗糙钛板的BRDF受入射光波长变化影响较大,在本文研究的入射光波长范围内,增幅最大达到41.0%。当表面粗糙度较大时,光子在粗糙表面内会经历多次散射,导致镜反射特性减弱,漫反射特性增强,粗糙表面内多次散射光子数比例随着表面粗糙度的增大而增加,当表面粗糙度相同时,多次散射光子数比例随着入射角度的增大有增加的趋势。
参考文献
[1]杨世铭,陶文铨.传热学(第四版)[M].北京:高等教育出版社,2006:351-383.(Yang Shiming,Tao Wenquan.Heat Transfer (4th Ed) [M].Beijing: Higher Education Press,2006:351-383.)
[2]余其铮.辐射换热原理[M].哈尔滨:哈尔滨工业大学出版社,2000:28-35.(Yu Qizheng.Principle of Radiative Heat Transfer [M].Harbin: Harbin Institute of Technology Press,2000:28-35.)
[3]Modest M F.Radiative heat transfer (2nd Ed) [M].San Diego: Academic Press,2003.
[4]Renhorn I G E,Boreman G D.Analytical fitting model for rough-surface BRDF [J].Opt Express,2008,16(17): 12892-12898.
[5]Fu K,Hsu P.New regime map of the geometric optics approximation for scattering from random rough surfaces [J].J.Quant.Spectrosc.Radiat.Transfer,2008,109(2): 180-188.
[6]Chen Y B,Zhang Z M,Timans P J.Radiative properties of patterned wafers with nanoscale linewidth [J].J Heat Transfer,2007,129(1): 79-90.
[7]黄志锋.高方向分辨率辐射强度及表面辐射特性计算研究[D].武汉:华中科技大学,2010.(Hang Zhifeng.Study of surface radiative properties and radiative intensity with directional high resolution [D].Wuhan: Huazhong University of Science and Technology,2010)
[8]帅永,刘彬.微粗糙硬铝表面双向反射特性实验研究[J].工程热物理学报,2010 (4): 671-674.(Shuai Yong,Liu Bin.Experimental study on bidirectional reflectance distribution function from micro-rough duralumin surfaces[J].J Eng Thermophys,2010(4):671-674)
[9]Bass M.Handbook of Optics Vol.Ⅳ,Optical properties of materials,nonlinear optics,quantum optics (3rd Ed) [M].New York : McGraw-Hill Comp,Inc,2009.
[10]Palik E D.Handbook of Optical Constants of Solids [M].Orlando: Academic Press,1985:369-406.
[11]Palik E D.Handbook of Optical Constants of Solids Ⅲ [M].Orlando: Academic Press,1998:240-249.
[12]Bergstrom D,Powell J,Kaplan A.Aray-tracing analysis of the absorption of light by smooth and rough metal surfaces [J].J Appl Phys,2007,101(11): 113504/1-11.
[13]谈和平,夏新林,刘林华,等.红外辐射特性与传输的数值计算:计算热辐射学[M].哈尔滨:哈尔滨工业大学出版社,2006:157-172.(Tan Heping,Xia Xinlin,Liu Linhua,etal.Numerical simulation of infrared radiation characteristics and transmission: Computation of thermal radiation [M].Harbin: Harbin Institute of Technology Press,2006:157-172)
[14]Zhang W J,Zhao J M,Liu L H.Experimental Study of the Effective BRDF of a Copper Foam Sheet[J].Proceedings of the 7th International Symposium on Radiative Transfer,Kusadasi,Turkey,June 2-8,2013: RAD-13-SH4.
Characteristics of BRDF on Surface of Common Metal Materials Applied on Space Camera
GUAN Hong-yu,LIU Ju*,YU Shan-meng,GUAN Feng-wei
(ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun,130033,China)
Abstract:In order to guarantee the accuracy and reliability in calculation of surface radiative heat transfer in thermal design of space camera,based on the optical constants of two metal materials,the bidirectional reflectance distribution function (BRDF) of their rough surfaces was studied by using the geometrical optical approximation and Monte Carlo ray tracing method.The influence of wavelength of incident light,incident angles and surface roughness on the BRDF of rough surface of aluminum and titanium is analyzed.The results indicate that the distribution of BRDF on rough surface of aluminum and titanium material has clear mirror reflection characteristic,the peak value of BRDF in the incident surface increases with the wavelength increasing of incident light,in the range of wavelength studied in this paper,BRDF of the titanium surface increasing with the wavelength of incident light increases up to 41.0%,far higher than 8.7% of the aluminum surface.When roughness is larger enough,the photon will experience multiple scattering in the rough surface,the ratio of multiple scattering photons in the rough surface increases with the surface roughness increasing,and has increasing trend as the incident angle increases.
Key words:surface radiation; rough surface; geometrical optics approximation; BRDF
中图分类号:TK121
文献标志码:A
doi:10.13883/j.issn1004-5929.201601013
作者简介:关洪宇(1989-),男,黑龙江省哈尔滨市人,研究实习员,主要研究工作是空间相机热设计。E-mail:guan_hongyu123@126.com通讯作者:刘巨,E-mail: yanwuqiu@yahoo.com.cn
基金项目:国家自然科学基金资助项目(60506014)
收稿日期:2015-06-25; 修改稿日期: 2015-07-13
文章编号:1004-5929(2016)01-0077-07
