转角多层石墨烯层间耦合的共振拉曼光谱研究

吴江滨，张昕，韩文鹏，乔晓粉，M.Ijäs，A.C.Ferrari,谭平恒*

(1.中国科学院半导体研究所，半导体超晶格国家重点实验室，北京　100083;

2.CGC,University of Cambridge,9 JJ Thomson Avenue,Cambridge CB3 0FA,UK)



转角多层石墨烯层间耦合的共振拉曼光谱研究

吴江滨1，张昕1，韩文鹏1，乔晓粉1，M.Ijäs2，A.C.Ferrari2,谭平恒1*

(1.中国科学院半导体研究所，半导体超晶格国家重点实验室，北京100083;

2.CGC,University of Cambridge,9 JJ Thomson Avenue,Cambridge CB3 0FA,UK)

摘要:我们通过共振拉曼光谱测量了转角多层石墨烯的层间振动模式：剪切模和呼吸模。根据改进的线性模型，我们发现在转角多层石墨烯界面处的层间呼吸耦合与正常Bernal堆垛多层石墨烯的强度相当。此结果明显不同于层间剪切耦合，后者在转角多层石墨烯界面处的层间剪切耦合减弱到了正常Bernal堆垛多层石墨烯的20%。另外，我们首次发现层间呼吸耦合存在着次近邻原子层之间的相互作用，其强度为最近邻的9%。我们发现当采用与界面层间旋转角度相对应的激发光时，转角多层石墨烯的拉曼信号得到极大的增强。为此，我们引入光学跃迁允许的电子联合态密度的概念，通过理论计算，我们发现这种联合态密度的极大值决定了拉曼信号共振线型的激发光能量极值。本研究表明，层间振动模式是探测二维层状异质层间耦合的有效手段，为其在器件应用方面的研究奠定了基础。

关键词：石墨烯;层间剪切模;层间呼吸模;二维异质结;拉曼光谱

1引言

以石墨烯为代表的二维材料具有优良的电学性能和光学性能，因此被期待可用来发展更薄、导电速度更快的新一代电子元件，晶体管和光电器件[1-3]。将石墨烯堆叠起来可以得到多层石墨烯[4]。除了具有和体石墨相同的Bernal堆垛(即AB堆垛)方式的多层石墨烯之外[5]，还可以在实验室制备或者合成出不同石墨烯片层取向随机的多层石墨烯，即转角多层石墨烯[6-9]。转角多层石墨烯内各子系统的层数不同和各子系统间旋转角度的不同将使得其具有无限多的可能性，这无疑大大丰富了石墨烯材料的研究对象和研究内容：例如单层或多层石墨烯堆垛方式的差异有可能导致石墨烯片层不同的层间耦合，从而影响其电子能带结构，使得转角多层石墨烯具有与其堆垛方式相应的各种各样的光电性质[10-15]。因此，探测和理解这种层间耦合就变得至关重要。

二维层状材料的层间剪切模(C模)和层间呼吸模(LBM)直接反映了层间耦合的性质[16-17]。对于一个N层的层状二维材料，存在N-1个的C模和LBM模，我们将其记为CNN-i和LBMNN-i(i=1,2,…,N-1)，其中CN1和LBMN1表示频率最高的模式[8-9,18]。多层石墨烯的C模已经被成功地观测到，并且可以用来探测狄拉克点(Dirac point)附近能量为几个meV的电子激发[19]。到目前为止，因为对称性和相对弱的电声子耦合等原因，多层石墨烯的LBM在常温下还未能被观察到[20]。

在这里，我们将层数为n的AB堆垛的石墨烯(nLG，n≥1)和层数为m的AB堆垛的石墨烯(mLG，m≥1)以一定的角度θ堆垛到一起，形成m+n层的转角多层石墨烯(t(m+n)LG)。通过选择与旋转角度相对应的激发光，系统地探测了t(m+n)LG的C模和LBM。我们发现在t(m+n)LG中探测到了来自nLG和mLG的C模和来自t(m+n)LG的LBM。通过改进的线性原子链模型[21](LCM)拟合发现转角界面处的剪切耦合为AB堆垛界面处的20%，而呼吸耦合并没有明显的变化。此外，我们发现存在着次近邻原子层的呼吸耦合，其强度为最近邻原子层耦合的9%。最后，我们提出了“光学跃迁允许的联合态密度(JDOSOAT)”的概念，很好地解释了在t(m+n)LG中拉曼信号的共振增强现象。

2实验装置

本文所用的t(m+n)LG是通过机械剥离法或者转移法制备的。同时利用光学衬度方法[22-24](optical contrast)和原子力显微镜(atomic force microscopy)确定了样品层数。所涉及到的拉曼光谱测试是采用法国Horiba Jobin Yvon公司的LabRam HR800共焦显微拉曼光谱仪。所使用的能量为1.58和1.71 eV的激光是来自钛宝石激光器，能量为1.96，2.03，2.09和2.28 eV的激光是来自He-Ne激光器，能量为1.83，1.92，2.18，2.34和2.41 eV的激光是来自Kr+激光器，以及能量为2.54和2.67 eV的激光是来自Ar+激光器。为防止出现样品的加热效应，测试拉曼光谱所用的激光功率低于0.5mW。为了探测超低频率的拉曼信号，我们采用了四块光密度(optical density)为3，光谱带宽(spectral bandwidth)为5~10 cm-1的体布拉格光栅(BragGrate notch filters)去除瑞利线(Rayleigh line)。当激发光能量为2.41 eV时光谱分辨率为0.54 cm-1。转角多层石墨烯的能带结构是由DFTB+软件包[25-27]计算的。另外，我们采用紧束缚方法计算了光学跃迁矩阵元[28-29]。

3结果与讨论

图1a为t(1+1)LG和t(1+3)LG的光学图像，图1b展示了它们的光学衬度谱。与(m+n)LG相，比t(m+n)LG的光学衬度谱多出了一个吸收峰。这个吸收峰来自于界面层间旋转导致的能带结构变化，这点将在后文进行详细地讨论。图1c画出了t(1+3)LG的拉曼光谱。在G模两侧存在着两个相对较弱的模式，通常称其为R(1510 cm-1)和R’(1618 cm-1)模。这两个模式是来自于上下两层石墨烯旋转之后产生的超晶格[30]。根据这两个模式的频率我们可以定出这个t(1+3)LG界面处层间旋转角θ为10.6°。在37和22 cm-1处，我们观察到了两个C模，根据它们的频率，我们将其分别指认为C31和C32。同时在93和116 cm-1处，我们也观察到了两个相对较宽的模式。根据第一性原理计算的结果[31]，这个两个模式可以被指认为LBM42和LBM41。另外，通过对称性分析发现，t(m+n)LG (m≠n)具有C3对称性，其对应的C模和LBM的拉曼张量如下[32]：

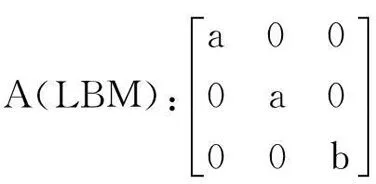
根据上述的拉曼张量，LBM在XX偏振配置下可以被观察到，而在XY偏振下看不到，但是C模在两种偏振下都可以被看到，而且强度相同。我们在图1c中画出了t(1+3)LG的偏振拉曼实验结果，与对称性分析的结论吻合，进一步证实了我们的指认。

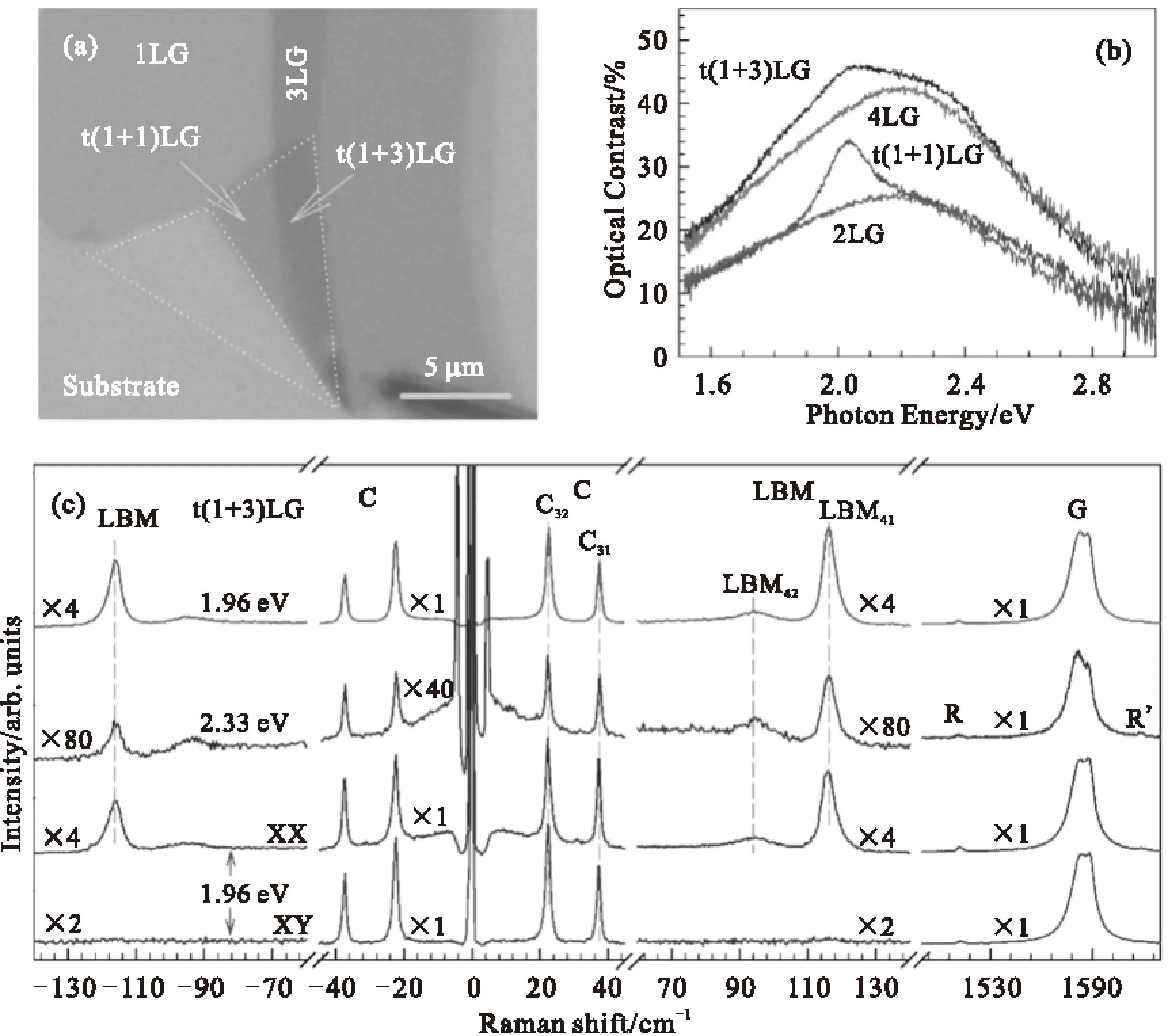
Fig.1(a) Optical image of a flake comprising a t(1+1)LG and a t(1+3)LG.(b) Optical contrast of t(1+1)LG and t(1+3)LG.For comparison,the contrast of 2LG and 4LG is also plotted.(c) Stokes/anti-Stokes Raman spectra in the C and LB spectral range,and Stokes Raman spectra in the G peak region for 1.96 and 2.33 eV excitation.Polarized Raman spectra are also shown

图2给出了t(1+2)LG,t(1+1+1)LG,t(1+3)LG,t(2+2)LG,t(2+3)LG和t(5+5)LG的拉曼光谱。它们的旋转角度与对应的激发光能量都被标注出来。我们在t(1+2)LG中观察到了C21(31 cm-1)模和LBM31(109 cm-1)，而在t(2+2)LG中观察到C21(31 cm-1)模和LBM41(109 cm-1)，在其他的t(m+n)LG中也观察到了类似的情况。也就是，我们在t(m+n)LG中观察了分别来自于nLG和mLG的C模和来自(m+n)LG的LBM。在t(m+n)LG中，转角的界面阻隔了层间的剪切耦合，使得C模局域在AB堆垛的子系统内。而这种阻隔对呼吸耦合并不起作用，因此LBM模仍为(m+n)LG的模式。

一般地，多层石墨烯等二维层状材料的C模和LBM的频率以及原子位移方式可以通过求解如下的线性齐次方程组得到[8]：

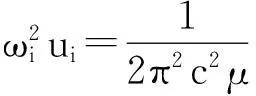
Fig.2Stokes/anti-Stokes Raman spectra in the C and LB peak region and Stokes spectra in the G spectral region for six tMLGs.Eexis also indicated.The spectra are scaled and offset for clarity.The scaling factors of the individual spectra are shown.Vertical lines are guides to the eye

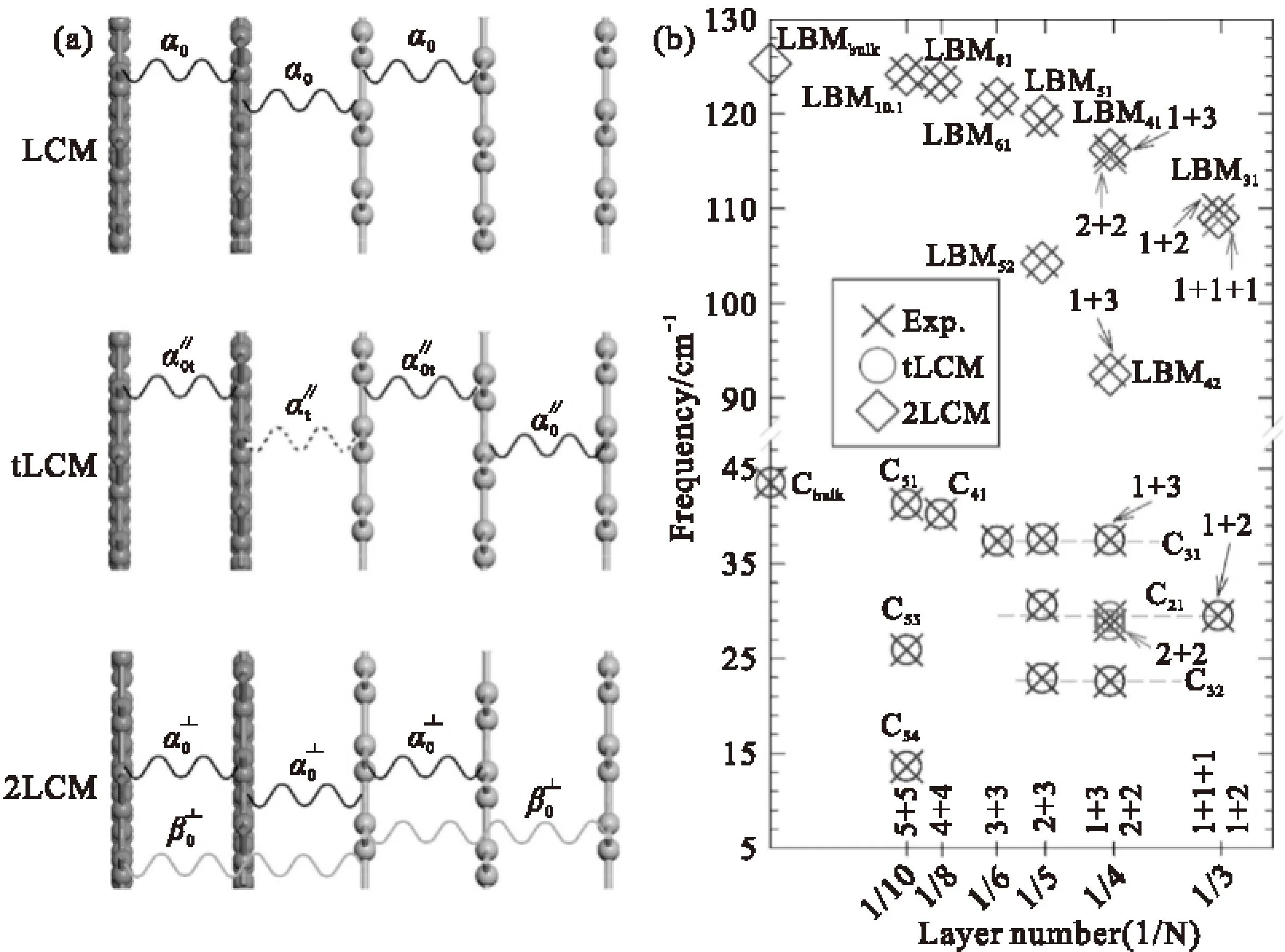
Fig.3(a) Linear chain model (LCM),LCM with the twisted interface (tLCM) and LCM with second-nearest interlayer coupling (2LCM).(b) Experimental (Exp.,open crosses) and theoretical (tLCM,open circles,and 2LCM,open diamonds) data of C and LB modes in tNLG

在图1c中，我们发现当激发光为1.96 eV时，t(1+3)LG的拉曼信号得到极大增强，是激发光为2.33 eV时的拉曼强度的30倍左右。由此可见，在t(m+n)LG中，存在着拉曼信号增强现象。共振拉曼信号的增强现象可以用二阶微扰理论来解释。因为只有光学跃迁允许的能带才能在拉曼过程中有贡献，在这里我们引入光学跃迁允许的联合态密度[8]：

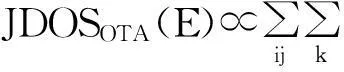
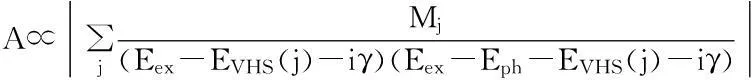
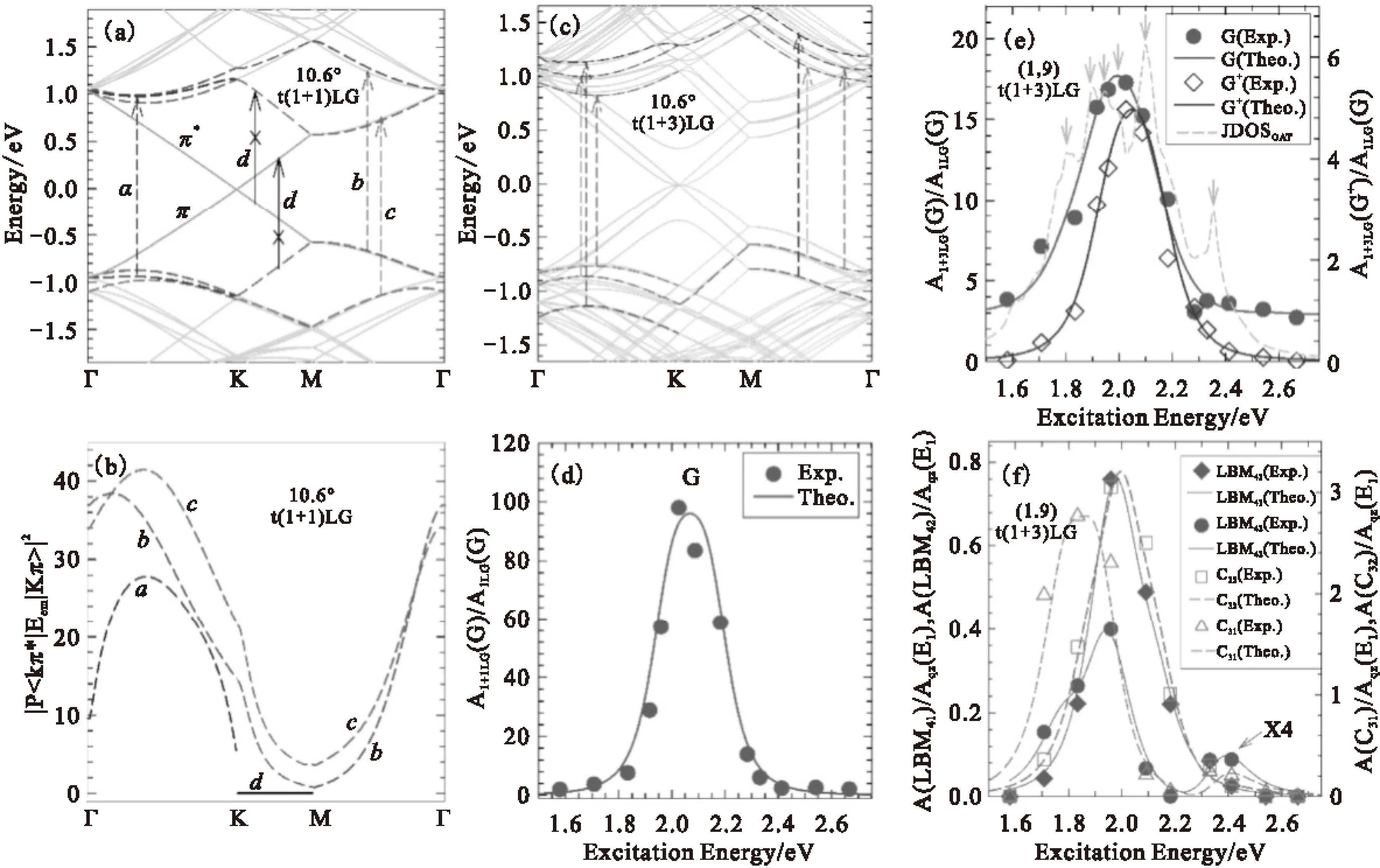
Fig.4(a) Band structure of 10.6° t(1+1)LG.The optically allowed transitions are marked by dashed arrows.The transitions with energy ~1.15 eV between parallel bands along K-M are forbidden,as indicated by solid arrows with crosses.(b) Squared optical matrix elements of the corresponding band pairs in (a).(c) Band structure of 10.6° t(1+3)LG.Some typical transitions are indicated by vertical dashed lines.(d) A(G) of t(1+1)LG,(e) A(G) and A(G+) of t(1+3)LG,and (f) A(C31),A(C32),A(LBM42) and A(LBM41) as a function of laser excitation energy.The filled circles,open diamonds,open triangles and open squares are the experimental data,while the lines show the simulations.The dash-dotted lines in (e) are the electronic joint density of states (JDOSs) of all the optically allowed transitions (JDOSOAT) in t(1+3)LG along G-K-M-G.The VHSs of JDOSOATare indicated with arrows

4结论

在本文中，我们通过机械剥离和转移方法制备了不同层数的t(m+n)LG。利用共振拉曼手段，系统地探测了t(m+n)LG的C模和LBM。在t(m+n)LG中，我们发现C模是局域在nLG和mLG子系统内的，而LBM是全局的。通过改进的线性原子链模型(LCM)拟合实验结果，我们发现转角界面处的剪切耦合为AB堆垛界面处的20%，而呼吸耦合并没有明显的变化。此外，我们还发现多层石墨烯存在着次近邻呼吸耦合，其强度为最近邻呼吸耦合的9%。最后，我们利用“光学跃迁允许的联合态密度(JDOSOAT)”的概念，很好地解释了在t(m+n)LG中拉曼信号的共振增强现象。本文的研究表明，层间振动模式是探测二维层状异质层间耦合的有效手段，为其在器件应用方面的研究奠定了基础。

参考文献

[1]Novoselov K S,Geim A K,Morozov S V,etal.Electric field effect in atomically thin carbon films [J].Science,2004,306(5696):666-669.

[2]Geim A K,Novoselov K S.The rise of graphene [J].Nature Materials,2007,6(3):183-191.

[3]Geim A K.Graphene:Status and Prospects [J].Science,2009,324(5934):1530-1534.

[4]Ohta T,Bostwick A,McChesney J L,etal.Interlayer interaction and electronic screening in multilayer graphene investigated with angle-resolved photoemission spectroscopy [J].Phys Rev Lett,2007,98(20):206802.

[5]Bernal J.The structure of graphite [J].Proc R Soc Lond A,1924,104:749-773.

[6]Suarez Morell E,Pacheco M,Chico L,etal.Electronic properties of twisted trilayer graphene [J].Phys Rev B,2013,87:125414.

[7]Tan P H,Wu J B,Han W P,etal.Ultralow-frequency shear modes of 2-4 layer graphene observed in scroll structures at edges [J].Phys Rev B,2014,89:235404.

[8]Wu J B， Zhang X，Ijäs M，etal. Resonant Raman Spectroscopy of Twisted Multilayer Graphene [J].Nat Commun,2014,5:5309.

[9]Wu J B,Hu Z X,Tan P H,etal.,Interface Coupling in Twisted Multilayer Graphene by Resonant Raman Spectros copy of Layer Breathing Modes [J].ACS Nano ASAP 2015.

[10]Dos Santos J L,Peres N，Neto A C.Graphene bilayer with a twist:electronic structure [J].Phys Rev Lett,2007,99:256802.

[11]Trambly de Laissardiere G,Mayou D， Magaud L.Localization of Dirac electrons in rotated graphene bilayers [J].Nano Lett,2010,10:804-808.

[12]Moon P，Koshino M.Optical absorption in twisted bilayer graphene [J].Phys Rev B,2013,87:205404.

[13]Li G,Luican A,Dos Santos J M B L,etal.Observation of Van Hove singularities in twisted graphene layers [J].Nat Phys,2010,6(2):109-113.

[14]Kim K,Coh S,Tan L Z,etal.Raman spectroscopy study of rotated double-layer graphene:misorientation-angle dependence of electronic structure [J].Phys Rev Lett,2012,108(24):246103.

[15]Havener R W,Zhuang H,Brown L,etal.Angle-resolved Raman imaging of interlayer rotations and interactions in twisted bilayer graphene [J].Nano Lett,2012,12(6):3162-3167.

[16]Zhang X,Han W P,Wu J B,etal.Raman spectroscopy of shear and layer breathing modes in multilayer MoS2[J].Phys Rev B,2013,87 (11):115413.

[17]Michel K H,Verberck B.Theory of rigid-plane phonon modes in layered crystals[J].Phys Rev B,2012,85 (9):094303.

[18]Cong C,Yu T.Enhanced ultra-low-frequency interlayer shear modes in folded graphene layers [J].Nat Commun,2014,5:4709.

[19]Tan P H,Han W P,Zhao W J,etal.The shear mode of multilayer graphene [J].Nat Mater,2012,11 (4):294-300.

[20]Lui C H,Ye Z,Keiser C,etal. Temperature-activated layer-breathing vibrations in few-layer graphene [J].Nano Letters,2014,14(8):4615-4621.

[21]张光寅，蓝国祥，王玉芳.晶格振动光谱学(第2版)[M].北京：高等教育出版社,2001：73-83.(Zhang guangyin,Lan guoxiang,Wang yufang.Lattice vibration spectroscopy(2ed)[M].Beijing:Higher Education Press,2001:73-83)

[22]Blake P,Hill E W,Neto A H C,et al.Making graphene visible[J].Applied Physics Letters,2007,91 (6):063124.

[23]Ni Z H,Wang H M,Kasim J,etal.Graphene Thickness Determination Using Reflection and Contrast Spectroscopy [J].Nano Letters,2007,7 (9):2758-2763.

[24]韩文鹏,史衍猛,李晓莉,等.石墨烯等二维原子晶体薄片样品的光学衬度计算及其层数表征[J].物理学报,2013,62(11):110702.(Han W P,Shi Y M,Li X Li,etal.The numerical-aperture-dependent optical contrast and thickness determination of ultrathin flakes of two-dimensional atomic crystals:A case of graphene multilayers [J],Acta Phys.Sin,2013,62(11):110702.)

[25]Aradi B,Hourahine B,Frauenheim T.DFTB+,a sparse matrix-based implementation of the DFTB method [J].J Phys Chem A,2007,111(26):5678-5684.

[26]Hourahine B,Sanna S,Aradi B,etal.Self-interaction and strong correlation in DFTB [J].J Phys Chem A,2007,111(26):5671-5677.

[27]吴江滨,张昕,谭平恒,等.旋转双层石墨烯的电子结构 [J].物理学报,2013,62(15):157302.(Wu J B,Zhang X,Tan P H,etal.Electronic structure of twisted bilayer graphene [J],Acta Phys Sin,2013,62(15):157302.)

[28]Venezuela P,Lazzeri M,Mauri F.Theory of double-resonant Raman spectra in graphene:Intensity and line shape of defect-induced and two-phonon bands [J].Phys Rev B,2011,84(3):035433.

[29]Coh S,Tan L Z,Louie S G,etal.Theory of the Raman spectrum of rotated double-layer graphene [J].Phys Rev B,2013,88(16):165431.

[30]Coh S,Tan L Z,Louie S G,etal.Theory of the Raman spectrum of rotated double-layer graphene [J].Phys Rev B,2013,88(16):165431.

[31]Dolling G,Brockhouse B N.Lattice vibrations in pyrolitic graphite [J].Phys Rev,1962,128(3):1120.

[32]London R.The Raman effect in crystals [J].Adv Phys,2001,50(7):813-864.

Interface Coupling in Twisted Multilayer Graphene by Resonant Raman Spectroscopy

WU Jiang-bin1,ZHANG Xin1,HAN Wen-peng1,QIAO Xiao-fen1,M.Ijäs2,A.C.Ferrari2,TAN Ping-heng1*

(1.StateKeyLaboratoryofSuperlatticesandMicrostructures,InstituteofSemiconductors,ChineseAcademyofSciences,Beijing,100083,P.R.China;2.CGC,UniversityofCambridge,9JJThomsonAvenue,CambridgeCB3 0FA,UK)

Abstract:The C and LB modes of t(m+n)LG are studied systematically by Raman spectroscopy.In the t(m+n)LG,the C modes of nLG and mLG and LBMs of (m+n)LG are observed.We fit the positions of C and LB modes by an improved linear chain model.We find the interlayer shear coupling at the twisted interface is ~20% of that at Bernal stacked interfaces,but the layer breathing coupling at the twisted interface is closed to that of Bernal interface.Moreover,the next-nearest interlayer interaction,which is 9% of the nearest interlayer interaction,must be considered for LBMs.The Raman intensity of the C,LB and G modes is significantly enhanced in t(m+n)LGs for specific excitation energies.This behavior is assigned to the resonance between van Hove singularities in the joint density of states of all optically allowed transitions in twisted multilayer samples and the laser excitation energy,during the optical absorption and emission steps of the Raman process.Beyond tMLGs,the interlayer interaction of other heterostructures can also be measured by Raman spectroscopy.

Key words:graphene;shear mode;layer breathing mode;2D heterostructure;Raman spectroscopy

通讯作者：谭平恒，E-mail：phtan@semi.ac.cn

中图分类号：O433.4

文献标志码：A

doi:10.13883/j.issn1004-5929.201601005

作者简介：吴江滨(1990-)，男，福建泉州，博士研究生，研究方向为二维层状材料光学性质，E-mail：jbwu@semi.ac.cn

基金项目：国家自然科学基金(11225421，11474277，11434010)

收稿日期：2015-07-11; 修改稿日期:2015-09-20

文章编号：1004-5929(2016)01-0016-07