基于扩展有限元的页岩水平井压裂裂缝扩展模拟

魏 波，陈军斌，谢 青，张 杰，王汉青，赵逸然

(西安石油大学 石油工程学院，陕西 西安 710065)



基于扩展有限元的页岩水平井压裂裂缝扩展模拟

魏 波，陈军斌，谢 青，张 杰，王汉青，赵逸然

(西安石油大学 石油工程学院，陕西 西安 710065)

摘要：考虑裂缝内流体流动和岩石受力变形，建立页岩水平井水力压裂裂缝扩展数学模型，采用扩展有限元方法求解该模型。分析水平主应力、岩石力学特征参数及注入速度对裂缝扩展长度的影响，并研究多条裂缝的扩展及转向规律。结果表明：岩石弹性模量越大，泊松比越小，形成的裂缝越长；最小主应力越小，压裂液注入速度越大，裂缝扩展长度越长。同时扩展的2条裂缝之间存在应力干扰使裂缝向外转，裂缝间距越近，转向越明显。3条裂缝同时扩展，中间裂缝受到左右两边裂缝的制约作用，起裂较晚，扩展受到限制；随着压裂时间的延长，中间裂缝会摆脱两边裂缝的影响，冲出应力干扰区。

关键词：水力压裂；水平井；页岩储层；多裂缝干扰；数值模拟；扩展有限元法

魏波，陈军斌，谢青，等.基于扩展有限元的页岩水平井压裂裂缝扩展模拟[J].西安石油大学学报(自然科学版)，2016，31(2)：70-75,81.

WEI Bo,CHEN Junbin,XIE Qing，et al.Simulation of hydraulic fracturing crack propagating of horizontal shale well based on extended finite element method[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(2):70-75，81.

引言

近年来，水力压裂技术成为页岩储层改造的重要手段之一。页岩储层水力压裂裂缝扩展过程是一个复杂的非线性、多物理场耦合的过程[1]，需要综合研究地层岩石变形、流体流动以及断裂扩展等条件。水力压裂过程极其复杂，本文通过数值模拟法分析裂缝扩展过程。关于水力压裂裂缝模拟方法，国内外学者应用位移不连续法[2]、有限元法[3]、扩展有限元法[4]，其中，扩展有限元法由于能够精细描述岩石内部裂缝的几何形态，有效克服裂缝尖端高应力区和变形集中区奇点网格划分困难，并且具有计算速度快等其他方法无法比拟的优势，越来越受到国内外学者的关注[5]。2009年，Lecampion[6]研究了基于扩展有限元法的裂缝扩展过程，但是没有考虑流体不断注入撑开岩石的流固耦合作用。2012年，Keshavarzi等[7]基于扩展有限元法模拟裂缝扩展，但假设裂缝内流体压力保持恒定，与实际情况不符。2013年，Chen[8]建立了水力裂缝扩展有限元数学模型，并验证了扩展有限元模型的准确性与实用性。2014年，姚军等[9]研究了基于扩展有限元法的裂缝扩展过程，得到页岩脆性参数及注入速度对裂缝形态的影响，但多条水力裂缝的相互作用没有体现。

流固耦合以及裂缝之间的干扰等因素对裂缝扩展有重要的影响。针对上述问题，建立了页岩储层水平井水力压裂裂缝扩展有限元模型，并对单条裂缝与多条裂缝进行模拟实验，分析了水平主应力、页岩弹性模量、泊松比以及注入速度对裂缝扩展长度的影响，并分析多条水力裂缝扩展规律。

1水力压裂模型

1.1物理模型

页岩储层具有很强的非均质性与各向异性，在实际研究中非常复杂。为突出研究的重点，将页岩储层水力裂缝扩展域Ω假设为均质、各向同性的二维平面应变模型(图1)。ΓF，Γu，Γf分别为外力、位移及裂缝边界。在外力边界上受到外部载荷F的作用，裂缝面上受到流体压力p以及水平主应力σH、σh的作用。注入流量为Q0、漏失量为ql，形成的裂缝长度为L、宽度为w。裂缝的扩展被视为准静态的、没有流体的滞后。

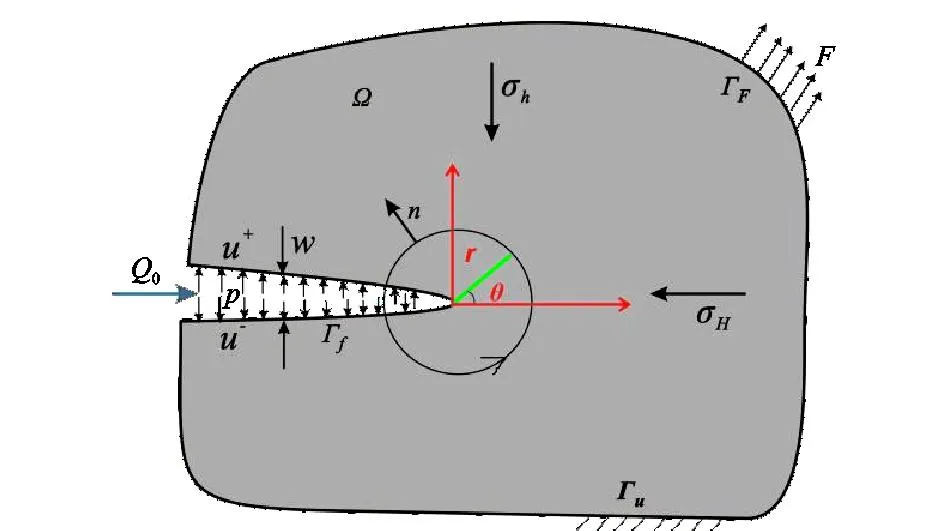
图1　水力裂缝扩展Fig.1　Propagation of hydraulic fracture

1.2岩石变形控制方程

岩石内部应力σ与外部载荷F及流体压力p之间满足关系[8]:

在ΓF上，σ·n=F；

(1)

在Γf上，σ·n-=-σ·n+=-pn+=pn-。

式中：n为单位法线向量。

用于描述位移边界条件及裂缝表面分离的应变与位移满足关系：

在Ω上，ε=(u+(u)T)/2；

在Γu上，u=0；

(2)

在Γf上，w=u+-u-。

式中：u为位移；ε为应变。

应力与应变关系满足本构方程

σ=Dε。

(3)

式中：D为弹性矩阵。

1.3流体流动控制方程

裂缝内的流体流动满足润滑理论和连续性方程

(4)

(5)

式中：μ为压裂液的黏度；q为裂缝延伸单位长度的流体流量。

流体流动的边界条件：

在入口处，流体流量等于注入量，即

q(0)=Q0；

(6)

在裂缝尖端，流体流量与裂缝开度为0，即

w(L/2)=0,q(L/2)=0。

(7)

式中：L/2为裂缝半长。

压裂裂缝扩展判据满足岩石失稳条件：岩石应力强度因子KI值达到其断裂韧性KIC时裂缝失稳扩展，即

KI≥KIC。

(8)

2水力压裂模型离散

2.1扩展有限元法

扩展有限元法(XFEM)最早是由Moes等[10]提出的一种描述位移不连续问题的有限元修正方法，具有较强的实用性及方便性。核心思想在于用扩充的带有不连续性质的形函数来描述裂缝域内的间断，不连续场的描述完全独立于网格边界，裂缝路径与尖端不需要网格重构与加密，并且裂缝以任意方向延伸，不需要预先设定，更反映实际的裂缝扩展规律。网格划分简单，计算耗时短[11-12]。

基于扩展有限元格式的裂缝周围位移场的近似式[13]为

(9)

H(x)=±1；

(10)

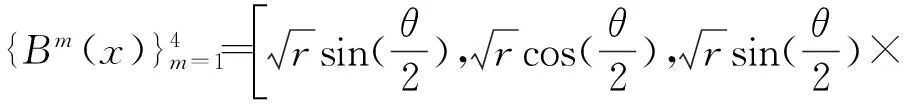
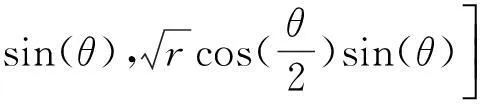
(11)

式中：I为网格中所有的节点集合；Icr为被裂缝完全贯穿的节点集合，用阶跃形函数H(x)描述；Itip为没有被裂缝完全贯穿的节点集合，用尖端形函数B(x)描述；Ni(x)为单元节点形函数，Nj(x)为单元中含有间断的节点形函数；ui为位移节点自由度；aj与bjm分别为描述裂缝路径与尖端额外节点自由度。

裂缝内的流体压力可用标准有限元法进行近似，即

(12)

2.2水力压裂控制方程离散

岩体变形方程的扩展有限元离散[14]为

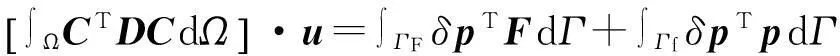
(13)

式中：C为应变转换矩阵；CTDC表示刚度矩阵；δp为虚压力。

裂缝内流体流动控制方程的弱形式[8]：

(14)

将式(13)与(14)耦合求解，即可得到裂缝在流体压力作用下的几何形态。

3模型求解及结果分析

模拟求解耦合了流体流动与岩石变形，注入流体通过射孔孔眼与岩石沟通，并不断作用于射孔孔眼表面，当满足断裂条件时，新裂缝生成，并在流体压力作用下不断延伸，这一耦合过程通过式(13)与(14)准确描述，并通过扩展有限元法反复迭代求解，得到裂缝扩展的位移场与应力场。

3.1模型参数取值

模型参数见表1。计算结果与经典模型(KGD)[15]进行对比(图2)，验证模型的准确性。KGD是水力压裂解析模型，是一种简化模型，不对裂缝体进行网格划分，灵活度较低。而有限元模型通过数值求解得到裂缝路径上每一个单元节点的位移，最终得到裂缝的位移场，更能反映实际的裂缝结构断裂与扩展规律以及裂缝之间相互作用的转向规律，这是KGD模型不能得到的。

表1　计算参数取值

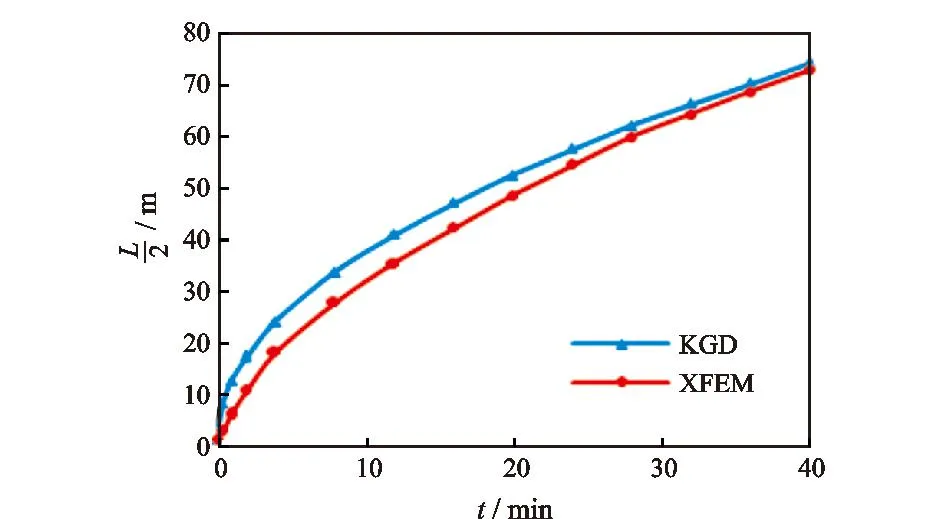
图2　本文模型与KGD模型结果对比Fig.2　Comparison of results obtained by the XFEM model with the KGD model

3.2结果分析

3.2.1单条裂缝扩展规律页岩储层水平井水力压裂单条裂缝数值模拟求解得到的最大主应力分布与位移变化情况分别如图3(a)与(b)所示。由图3(a)可知，裂缝沿着最大主应力的方向延伸，尖端出现应力集中现象，应力值最大；由图3(b)可知，注入点处，裂缝张开位移最大。裂缝扩展的应力分布与位移变化规律与实际情况相符。

页岩储层中，弹性模量、泊松比、水平主应力以及注入速度对裂缝扩展长度的影响如图4所示。

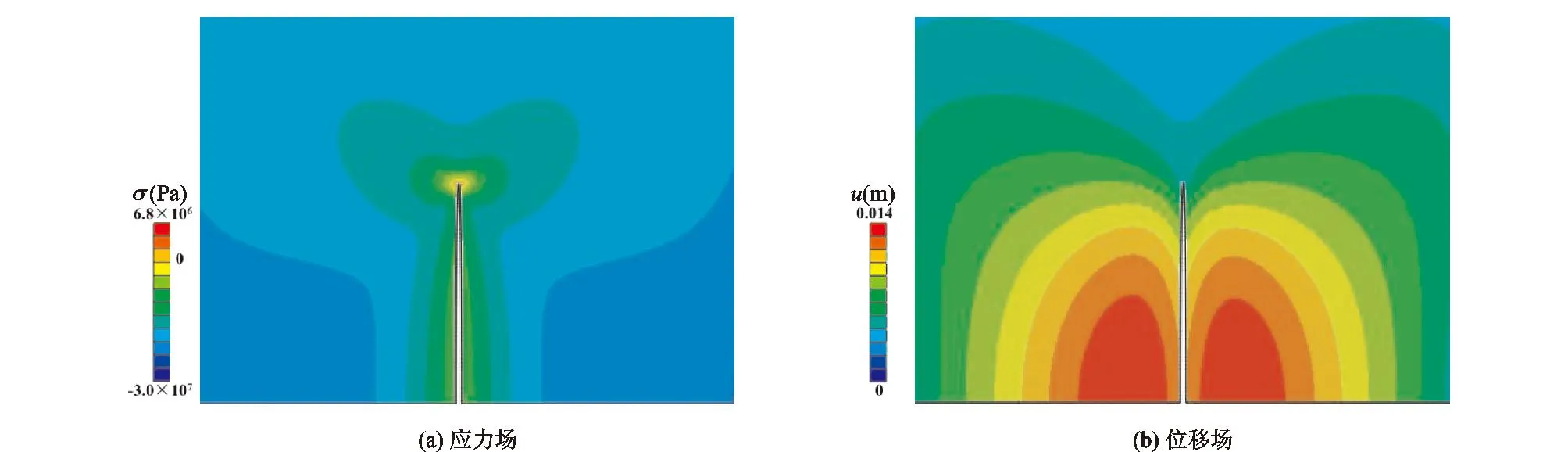
图3　单条压裂裂缝扩展的位移场与应力场Fig.3　Displacement field and stress field in the propagation of single fracture

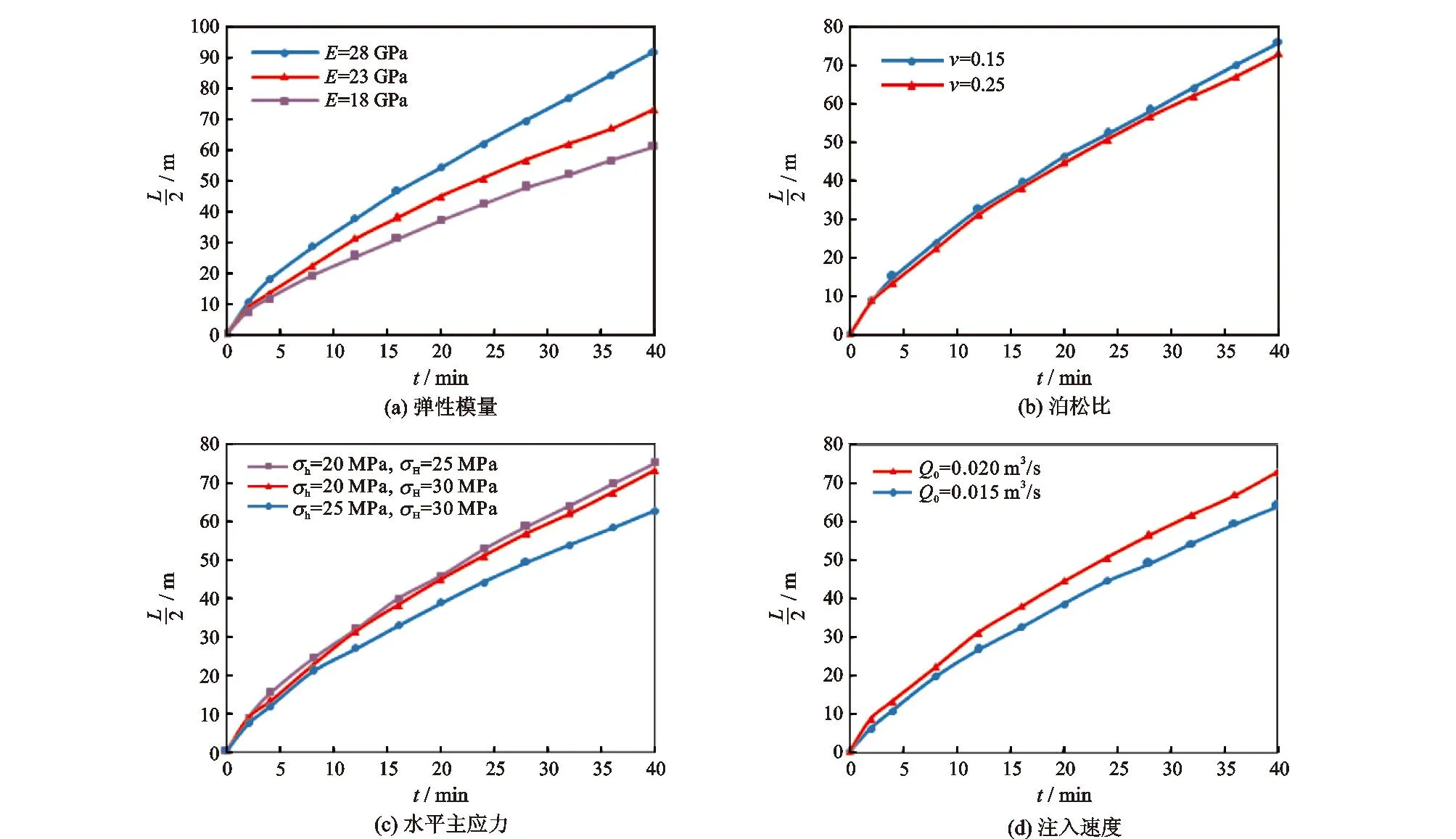
图4　压裂裂缝扩展半长随压裂时间的关系曲线Fig.4　Varying curves of half length of fracturing fracture with time in the propagation process

由图4(a)与图4(b)可知，弹性模量对裂缝扩展长度的影响比泊松比的影响大得多。高弹性模量、低泊松比的页岩储层脆性矿物含量越高，受到流体压力的作用更容易发生脆性破裂，同样的压裂时间下，高弹性模量、低泊松比的储层裂缝扩展长度越长。由图4(c)可知，当水平主应力差等于5 MPa与10 MPa时，发现裂缝长度的变化不明显，说明应力差对裂缝长度的影响较小。保持最大主应力值不变，改变最小主应力的值，压裂40 min，发现σH=25 MPa时，裂缝半长为62.7 m；σH=20 MPa时，裂缝半长为71.3 m。说明最小水平主应力是制约裂缝起裂与扩展的重要因素。由图4(d)得出，流体注入速度越大，压力加载速率越快，裂缝起裂越早，相同压裂时间下，裂缝延伸越长。

3.2.22条裂缝的扩展规律本算例设计2条相距25 m的裂缝，扩展过程的最大主应力分布如图5(a)所示，裂缝张开位移变化规律如图5(b)所示。

由图5(a)可知，2条同时扩展的裂缝之间存在较强的应力干扰，这种相互作用迫使应力场发生变化，改变了裂缝延伸方向，发生相斥转向。裂缝转向

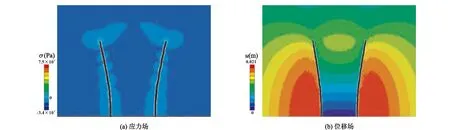
图5　间隔25 m 2条裂缝扩展的应力场与位移场Fig.5　Displacement field and stress field in the propagation of two fractures with interval of 25 m

造成裂缝面不平滑，最大主应力分布在裂缝周围出现不连续，裂缝宽度减小，并增加流体的流动阻力，不利于压裂液的流入与支撑剂的填充。从图5(b)可知，2条裂缝的外边入口处横向位移较大，越向边界，横向位移逐渐减小，到边界位移为0，2条裂缝中间区域位移变化很小，甚至中间区域没有横向位移，说明流体在垂直于裂缝壁面的法向产生挤压力，由于裂缝面两边同时受到作用力，在水平方向上相反的挤压力相互抵消，造成中间区域裂缝横向位移大大降低，最终引起裂缝宽度的减小。

为了研究裂缝干扰作用强弱与裂缝间距之间的关系，算例设计2条间距为45 m的裂缝，最大主应力分布与裂缝张开位移变化分别见图6(a)与图6(b)。从图6(a)中裂缝转向程度与应力分布发现，间距为45 m的裂缝面比间距为25 m的裂缝面更加平滑，说明裂缝干扰作用的强弱与裂缝间距有很大的关系，裂缝间距与干扰作用呈负相关关系。通过对比图5(b)与图6(b)，45 m间距的2条裂缝中间区域横向位移有增加的趋势，说明裂缝间应力干扰对裂缝宽度具有制约作用。

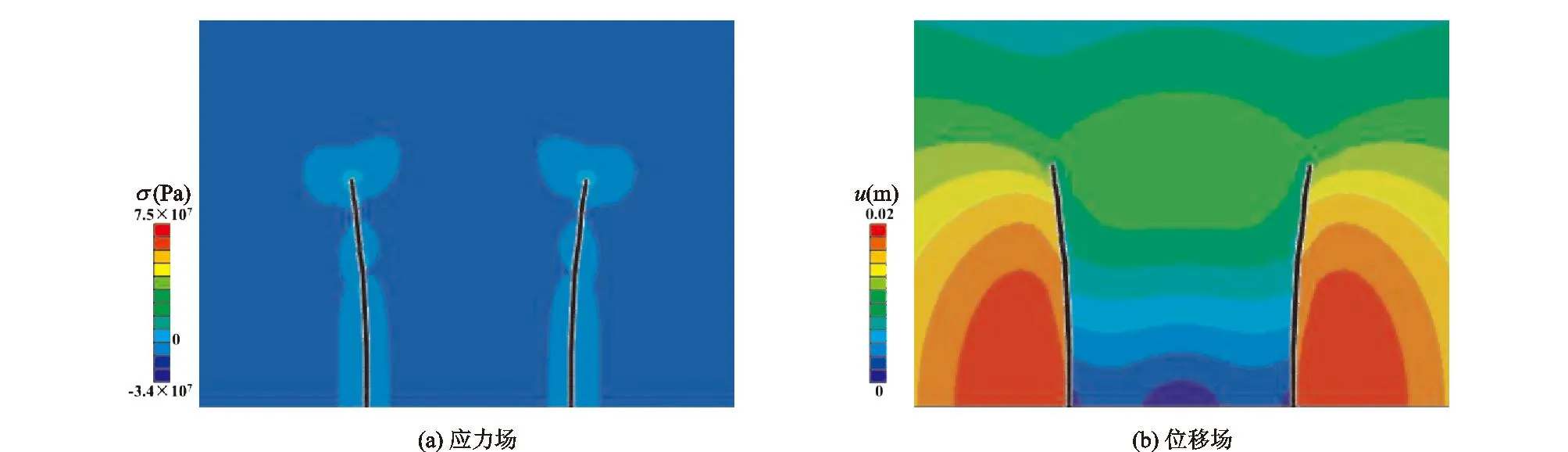
图6　间隔45 m 2条裂缝扩展的应力场与位移场Fig.6　Displacement field and stress field in the propagation of two fractures with interval of 45 m

3.2.33条裂缝的扩展规律算例设计3条间隔为25 m的裂缝在流体压力作用下的扩展过程，研究3条裂缝的起裂、扩展及转向规律。最大主应力分布及裂缝扩展规律如图7所示。

由图7可知：t=1.5 min时，左右两边的裂缝开始起裂，这是由于外侧的2条裂缝在压力加载过程中会对中间裂缝施加额外的力，致使中间裂缝应力场发生变化，起裂变得困难，起裂时间较晚。t=6.0 min时，左右两边的裂缝开始发生轻微转向。t=10.5 min时，左右两边裂缝发生较大程度的转向，从这一时间的最大水平主应力场图看出，同时扩展的裂缝之间存在应力干扰，改变最大水平主应力的方向，促使裂缝发生相斥转向。t=18.0 min时，左右两边裂缝发生较大角度的转向，降低了对中间裂缝的制约作用，中间裂缝突破了左右两边裂缝的应力干扰，并且加剧了左右两边裂缝的转向程度。t=22.0 min时，随着左右两边裂缝转向角度的增加，压裂液流动阻力增大，致使裂缝的扩展受到了制约，但对中间裂缝的扩展不造成影响。t=40.0 min时，中间裂缝的扩展长度明显大于两边裂缝，扩展长度是两边裂缝的1.76倍。为了使所有裂缝都能发生均匀扩展，必须选择合理的裂缝间距。

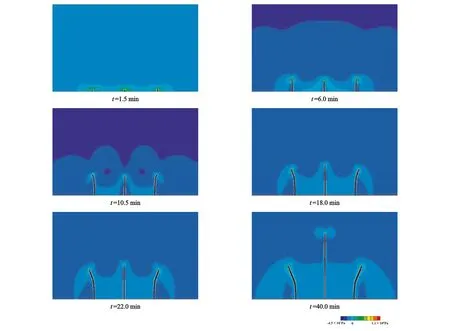
图7　3条间隔为25 m的裂缝扩展动态Fig.7　Dynamic diagram in the propagation of three fractures with interval of 25 m

4结论

(1)水平主应力差对裂缝长度的影响很小，最小主应力是制约裂缝扩展的主要因素，最小主应力越小，裂缝延伸长度越长；高弹性模量、低泊松比的岩石，裂缝延伸长度越长；注入速度越大，流体压力的加载速率越快，裂缝起裂越早，延伸长度越长。

(2)2条同时扩展的裂缝存在应力干扰作用，迫使裂缝延伸方向发生相斥转向，转向处裂缝宽度减小，曲折度增加；随着裂缝间距的减小，应力干扰作用越强，转向角度越大。

(3)3条裂缝同时扩展时，左右两边的裂缝先起裂延伸并对中间裂缝产生一定的制约作用，直到t=18.0 min之后，中间裂缝逐渐摆脱来自两边裂缝的影响，冲破应力干扰区，并加剧了两边裂缝的转向，大大减小了左右两边裂缝的扩展长度。为了使所有裂缝都能发生均匀扩展，必须选择合理的裂缝间距。

参 考 文 献：

[1]姚军，孙海，黄朝琴，等.页岩气藏开发中的关键力学问题[J].中国科学：物理学力学天文学,2013,43(12):1527-1547.

YAO Jun,SUN Hai,HUANG Zhaoqin,et al.Key mechanical problems in the development of shale gas reservoirs[J].China Science:Physica,Mechanica & Astronomica,2013,43(12):1527-1547.

[2]BEHNIA M,GOSHTASBI K,MARJI M F,et al.Numerical simulation of interaction between hydraulic and natural fractures in discontinuous media[J].Acta Geotechnica,2015,10(4):533-546.

[3]CHEN Z.Finite element modelling of viscosity-dominated hydraulic fractures[J].Journal of Petroleum Science and Engineering,2012,88:136-144.

[4]FRIES T P,BAYDOUN M.Crack propagation with the extended finite element method and a hybrid explicit-implicit crack description[J].International Journal for Numerical Methods in Engineering,2012.89(12),1527-1558.

[5]FRIES T P,BELYTSCHKO T.The extended/generalized finite element method:an overview of the method and its applications[J].International Journal for Numerical Methods in Engineering,2010,84(3),253-304.

[6]LECAMPION B.An extended finite element method for hydraulic fracture problems[J].Communications in Numerical Methods in Engineering,2009,25(2),121-133.

[7]KESHAVARZI R,MOHAMMADI S.A new approach for numerical modeling of hydraulic fracture propagation in naturally fractured reservoirs[C].Proceedings of SPE/EAGE European Unconventional Resources Conference & Exhibition-From Potential to Production.Vienna,Austria,2012:1-12.

[8]CHEN Z.An ABAQUS implementation of the XFEM for hydraulic fracture problems[C].In ISRM International Conference for Effective and Sustainable Hydraulic Fracturing.Brisbane,Australia,20 May 2013.

[9]曾青冬,姚军.基于扩展有限元的页岩水力压裂数值模拟[J].应用数学和力学,2014,35(11):1239-1248.

ZENG Qingdong,YAO Jun.Numerical simulation of shale hydraulic fracturing based on the extended finite element method[J].Applied Mathematics and Mechanics,2014,35(11):1239-1248.

[10] MOES N,DOLLOW J,BELYTSCHKO T.A finite element method for crack growth without remeshing[J].Int J Numer Methods Eng 1999,46(1):131-150.

[11] REN Q W,DONG Y W,YU T T.Numerical modeling of concrete hydraulic fracturing with extended finite element method[J].Sci China Ser E.2009,52(3):559-565.

[12] ZHOU L,GOU Y,HOU Z M.Numerical modeling and investigation of fracture propagation with arbitrary orientation through fluid injection in tight gas reservoirs with combined XFEM and FVM[J].Environ Earth Sci,2015,73(1):5801-5813.

[13] GOODARZI M,MOHAMMADI S,JAFARI A.Numerical analysis of rock fracturing by gas pressure using the extended finite element method[J].Petroleum Science,2015,12(2):304-315.

[14] WEBER N,SIEBERT P,WILLBRAND K,et al.The XFEM with an explicit-implicit crack description for hydraulic fracture problems[C].An ISRM specialized conference for Effective and Sustainable Hydraulic Fracturing.Brisbane,Australia,22 May 2013.

[15] GEERSMA J,KLERK F D.A rapid method of predicting width and extent of hydraulically induced fractures[J].Journal of Petroleum Technology,1969,21(12):1571-1581.

责任编辑：贺元旦

Simulation of Hydraulic Fracturing Crack Propagating of Horizontal Shale Well Based on Extended Finite Element Method

WEI Bo,CHEN Junbin,XIE Qing,ZHANG Jie,WANG Hanqing,ZHAO Yiran

(College of Petroleum Engineering,Xi'an Shiyou University,Xi'an 710065,Shaanxi,China)

Abstract:The mathematical model for the hydraulic fracturing crack propagating of horizontal well in shale reservoir was established under considering the flow of fluid in cracks and the deformation of rock,and it was solved using the extended finite element method.The influences of horizontal principal stress,the mechanics parameters of rock and the injection rate of fracturing fluid on the propagation length of cracks were analyzed,and the propagation and steering law of multiple fractures was researched.The results show that the greater the elasticity modulus of reservoir rock and the less the Poisson's ratio of it,the longer the fractures;the lower the minimum principal stress and the greater the injection rate,the longer the fractures.There is stress interference between two simultaneously propagating fractures,which makes two fractures turning to the outside.The closer the fractures are,the more obvious the steering is.When the three fractures simultaneously propagate,the fracture in middle is restricted,and its initiation is later than on both sides.With the fracturing time increasing,the middle fracture breaks away from the stress interference of the cracks on both sides and propagates.

Key words:hydraulic fracturing;horizontal well;shale reservoir;multi-fracture interference;numerical simulation;extended finite element method

文章编号：1673-064X(2016)02-0070-06

文献标识码：A

DOI：10.3969/j.issn.1673-064X.2016.02.011

中图分类号：TE357.1

作者简介：魏波(1987-)，男，硕士研究生，主要从事页岩气藏水平井压裂裂缝起裂与扩展规律研究。

基金项目：国家自然科学基金项目“页岩气藏水平井液态气动力压裂增产新方法研究”(编号：51374170)；西安石油大学优秀硕士学位论文培育项目(编号：2014yp130101)

收稿日期：2015-12-25

E-mail:xysuweibo131010097@163.com