基于EDEM与ADAMS耦合的冲击破碎仿真分析

刘志刚，蔡改贫，曾艳祥，卢小江，余世科（江西理工大学机电工程学院，江西赣州341000）



基于EDEM与ADAMS耦合的冲击破碎仿真分析

刘志刚，蔡改贫，曾艳祥，卢小江，余世科
（江西理工大学机电工程学院，江西赣州341000）

摘要：通过冲击破碎仿真模拟能使多尺度内聚颗粒呈现出较明显的弹性变形阶段、塑性变形阶段以及断裂破碎阶段。文章利用EDEM与ADAMS的双向耦合，对基于离散元法构建的钨矿石多尺度内聚颗粒模型进行冲击破碎仿真试验，通过仿真模拟发现，矿石多尺度内聚颗粒模型在冲击破碎过程中具有较明显的弹性变形阶段、塑性变形阶段以及断裂破碎阶段；分析得到了不同冲击角下破碎黏结键数目、冲击破碎力随时间的变化曲线，二者与冲击破碎能呈线性关系；对碎后的粒度进行筛分、统计，得到多尺度内聚颗粒模型破碎后粒度分布具有一定的单峰偏度正态特性，并与破碎试验结果进行对比，两者一致性较高，证实了利用多尺度内聚颗粒模型模拟矿石冲击破碎的可行性。关键词：双向耦合；离散元法；多尺度；冲击破碎

冲击破碎方法被广泛用于矿山、水泥、煤炭、交通等行业，但对于冲击破碎过程与机理研究仍相对滞后，因此，仍需对破碎机理进行深入细致地研究。

离散元法的出现为颗粒物料破碎模拟及其机理分析开辟了一条新思路，它能较好的求解连续介质向非连续介质转变的力学行为，直观反映颗粒破碎过程[1-2]，因此常被用于模拟矿石破碎。周博等人基于离散元方法（DEM）的双轴压缩试验研究了可破碎性土在剪切过程中颗粒破碎的演化过程，表明破碎率的增长速度随着剪切应变的发展逐渐降低[3]。徐佩华等人针对颗粒离散元法中颗粒碎裂与破碎动力学关系进行研究，为岩石工程领域的岩石颗粒破碎研究提供参考[4]。徐永福等人采用离散元法模拟岩石单颗粒压缩破碎试验，得出单颗粒破碎后颗粒分布的分维，验证单颗粒破碎强度的分形模型和单颗粒破碎强度的尺寸效应[5]。采用DEM模拟矿石破碎成果已有很多，但基于离散元法构建多尺度内聚颗粒模型，采用EDEM与ADAMS耦合模拟冲击破碎过程的研究成果不多见。

本文基于离散元法构建了矿石多尺度内聚颗粒模型，利用EDEM与ADAMS耦合仿真对双摆锤冲击破碎过程进行模拟，分析了不同冲击破碎角下黏结键数目、冲击破碎力的变化情况，通过对颗粒模型碎后粒度分布与试验结果比对，验证了采用多尺度内聚颗粒模型通过EDEM与ADAMS耦合来模拟矿石冲击破碎的可行性，可以为后续矿石冲击破碎机理的深入研究提供有益指导。

1基于EDEM的多尺度内聚颗粒模型的构建

在EDEM中，采用My Factory.dll插件生成多尺度内聚颗粒模型的几何形状，接着为模型增加内聚力，实现矿石内部的力学特性[6-7]。由矿石内部组成可知矿石由多种矿物组成，各矿物内部强度不一，同时不同矿物间存在脆性结合面等特点，由此构建四种不同类型的颗粒集合体fraction1、fraction2、fraction3、fraction4，如图1所示。通过黏结颗粒模型插件将上述四种颗粒集合体赋值不同的黏结颗粒模型参数，实现矿石内部的多种矿物组成。

对于矿石内部各矿物强度和矿物内部黏结强度不一的特点[8]，通过黏结颗粒模型插件，实现随机的法向刚度和切向刚度赋值，体现矿石内部同种矿物之间内聚力的差异性。为了体现矿石内部不同矿物结合面的脆性特点，将fraction1与fraction2，fraction1 与fraction3，fraction2与fraction4，fraction3与fraction4赋值更小的黏结强度。

最终通过fraction1、fraction2、fraction3、fraction4以及黏结颗粒模型插件，实现多尺度内聚颗粒模型具有矿石的各向异性、非均匀性、多元性、裂隙性、孔隙性等。

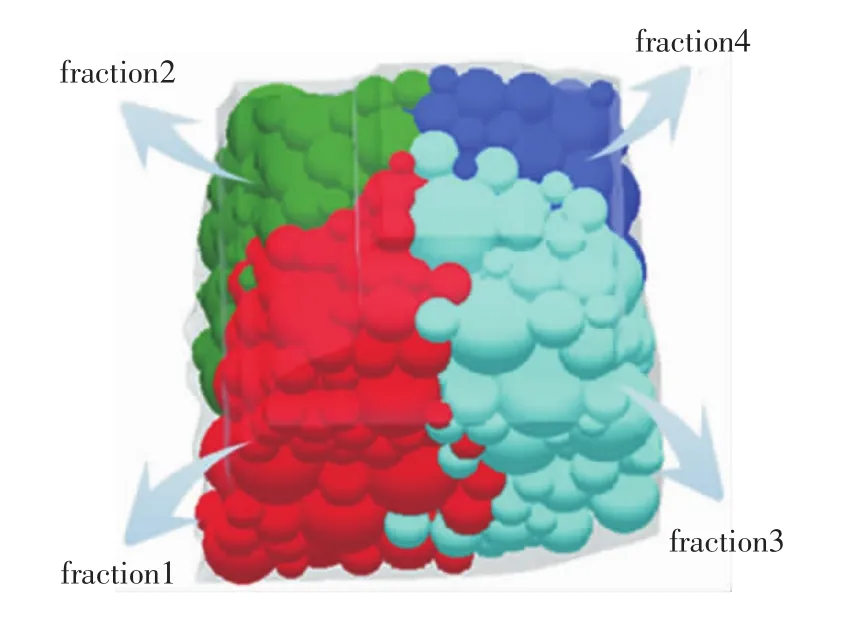
图1矿石颗粒模型不同类型的颗粒集合体Fig.1 Collection of different types of particles for ore particle model

材料本征参数是指自身的特性参数，即泊松比、剪切模量和密度。试验矿石为钨矿石，冲击摆锤为碳钢材料，其特性参数如表1所示。

表1材料属性参数Tab.1 Material property parameter

根据相应参数建立矿石多尺度内聚颗粒模型如图2所示，符合矿石特性同时符合冲击破碎特点的多尺度内聚颗粒模型。其中四种不同颜色的球，分别代表四种结构分布相同、不同类型颗粒集合体，如图2（a）所示；图2（b）中不同颜色、不同大小、不同长短的连接线表示不同黏结键，同种矿物间黏结键如图中字母a、b、c、d所示；不同矿物间脆性结合面的黏结键，如图中数字1、2、3、4标识所示。

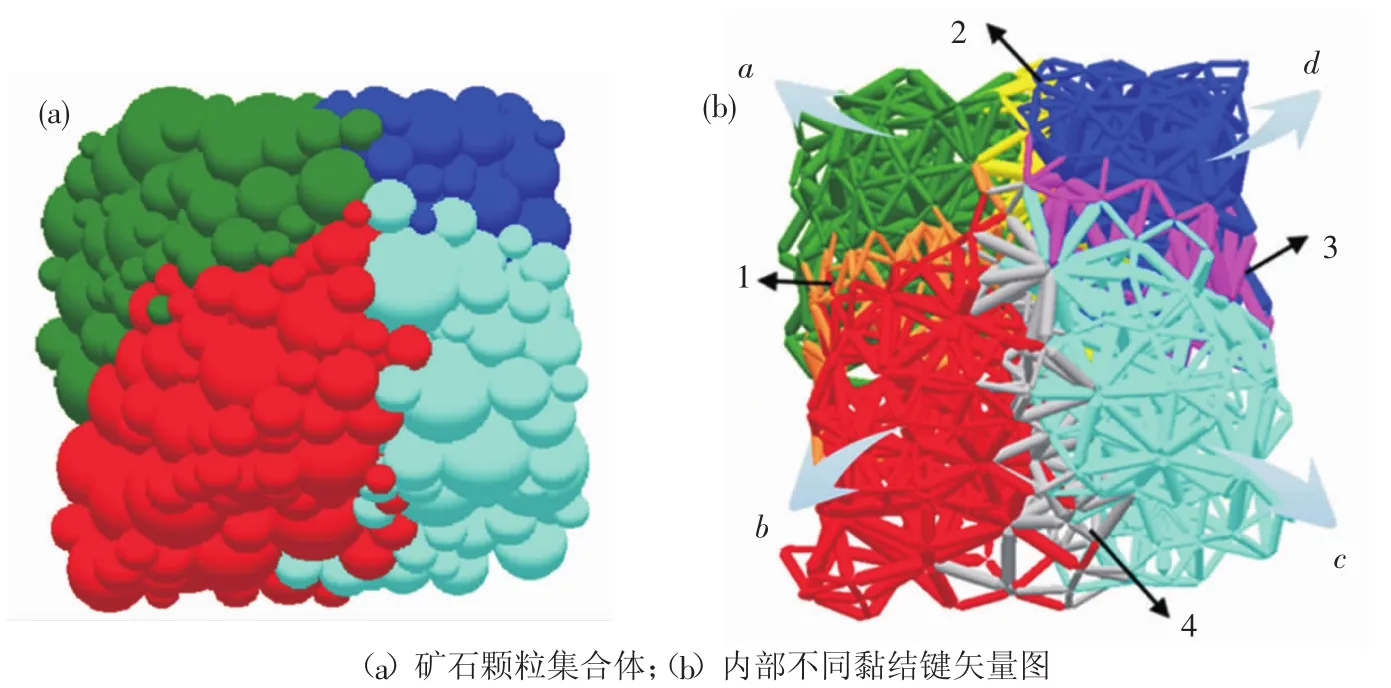
图2矿石多尺度内聚颗粒模型Fig.2 Multi-scale cohesive particle model

2冲击破碎仿真分析

2.1双摆锤仿真模型

在EDEM中导入的几何体可以实现平动、转动以及简单的复合运动，但导入几何体本身不具有质量，因而双摆锤模型摆锤几何体不会在EDEM重力场下自由摆动。因此，基于第三方软件EAlink实现EDEM与ADAMS的双向耦合，实现双摆锤对构建的多尺度内聚颗粒模型进行冲击破碎模拟，其中双摆锤冲击破碎实验机的几何模型如图3所示。

在ADAMS中，对各部件添加约束，将左摆锤（3）和右摆锤（5）分别提升至所需角度，设置ADAMS的重力场，实现摆锤在重力场下自由摆动。最后借助EAlink将EDEM中几何体部件与ADAMS各部件耦合。在每个时步，将ADAMS中7个部件运动数据与EDEM进行交换，实现双向耦合。

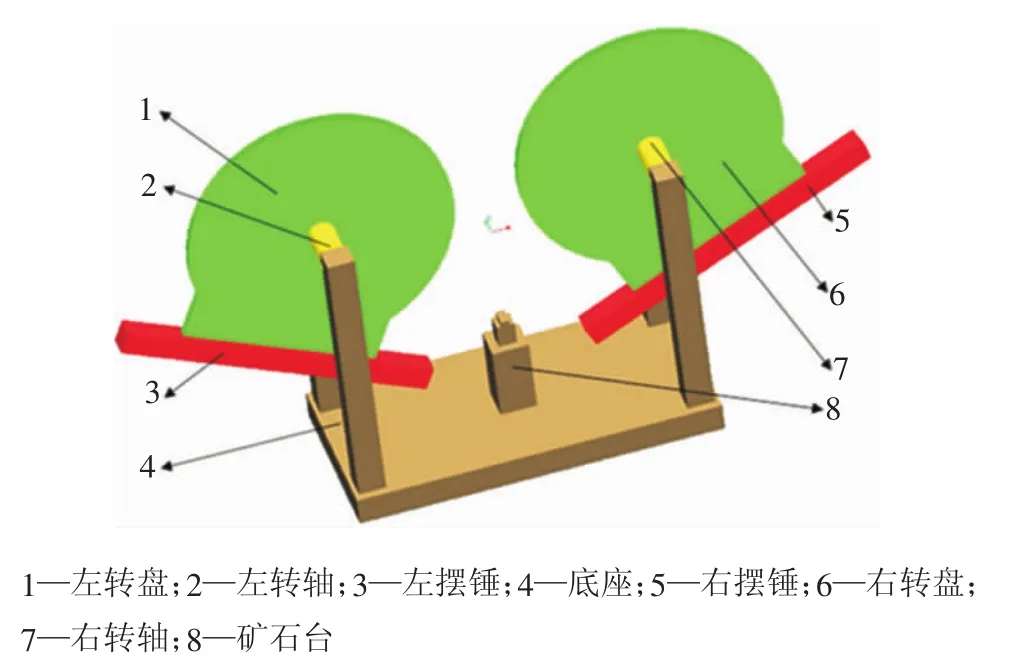
图3双摆锤简化模型Fig.3 Simplified model of double pendulum

2.2多尺度内聚颗粒模型冲击破碎过程模拟

根据构建的多尺度内聚颗粒模型，分析冲击角为30°、35°、40°、45°下，24 mm颗粒模型的破碎结果，见表2。

表2冲击破碎仿真试验方案Tab.2 Simulation experimental scheme of impact crushing

由于冲击破碎过程的时间短暂，采用试验方法分析破碎过程十分困难，而离散元法能够较好地反映矿石每个时步的破碎特征。通过EDEM后处理提取破碎后每个时步图片，如图4所示。

图4（a）为粒度为24 mm多尺度内聚颗粒模型，在冲击角为40°时冲击破碎仿真过程中的部分截图，分别表示模型在冲击破碎过程中挤压力大小的变化情况。

图4（a）中摆锤与矿石颗粒模型未接触，颗粒未受挤压力；图4（b）中，摆锤与矿石颗粒模型接触，内部颗粒挤压力剧增，并逐渐传递至整个矿石颗粒模型；图4（c）至图4（d）可以看出矿石在冲击破碎过程中也具有一定的弹性变形阶段，内部黏结键挤压变形，并开始断裂，同时由图可以看出矿石颗粒模型中间部位受力最大；图4（e）至图4（f）为矿石塑性变形至断裂的阶段，矿石颗粒模型逐渐变形破碎，内部黏结键快速断裂。图4（g）和4（h）为破碎后的结果，由此可以更为直观的观测破碎后的效果。

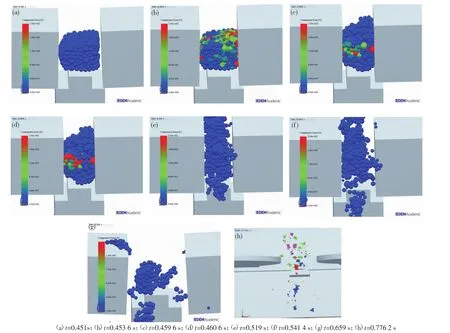
图4 24 mm多尺度内聚颗粒模型冲击破碎过程Fig.4 Impact crushing process for 24 mm multi-scale cohesive particle model

由图4（a）至图4（e）的破碎时间可以看出，多尺度内聚颗粒模型从摆锤接触到分离过程所用时间为0.06 s左右，这与实际矿石冲击破碎时间小于2 ms略有不符；这可能是由于计算机计算能力，使得构建的矿石颗粒模型填充的颗粒数目受限，致使矿石颗粒模型自身密度小于实际矿石密度且孔隙率大于实际矿石导致内部脆性变弱、弹性更高，增加了碰撞时间；虽然多尺度内聚颗粒模型仍存在一定误差，但总体上可以反映矿石的破碎过程。

2.3冲击破碎黏结键分析

为分析多尺度内聚颗粒模型在不同冲击破碎能下黏结键的断裂数目变化情况，以黏结键刚开始断裂时作为起始点，以0.000 5 s作为时间间隔，得到不同冲击角下剩余黏结键数量与时间步长的关系曲线，如图5所示。

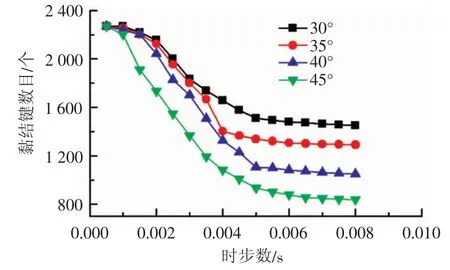
图5冲击破碎中黏结键数目与时间关系曲线Fig.5 Relationshipcurveofbondnumberandtimeduringimpact crushingprocess

由图5，对比30°、45°冲击角可以看出：冲击角越大，黏结键剩余数越少，这符合冲击破碎能越大矿石越碎的现象。多尺度内聚颗粒模型的初始形成时黏结键数目为2 270，在0.01 s的时间作用内，模型内部最终剩余黏结键趋于稳定；冲击角越大，黏结键断裂越迅速；从图5四种不同冲击角下颗粒模型黏结键的数目曲线中可以看出，在黏结键数目趋于稳定前，冲击破碎过程中黏结键数目随时间变化具有一定的线性特征。

以剩余黏结键数为纵坐标，以冲击破碎能为横坐标，可得到黏结键数目与冲击破碎能间曲线关系，如图6所示。

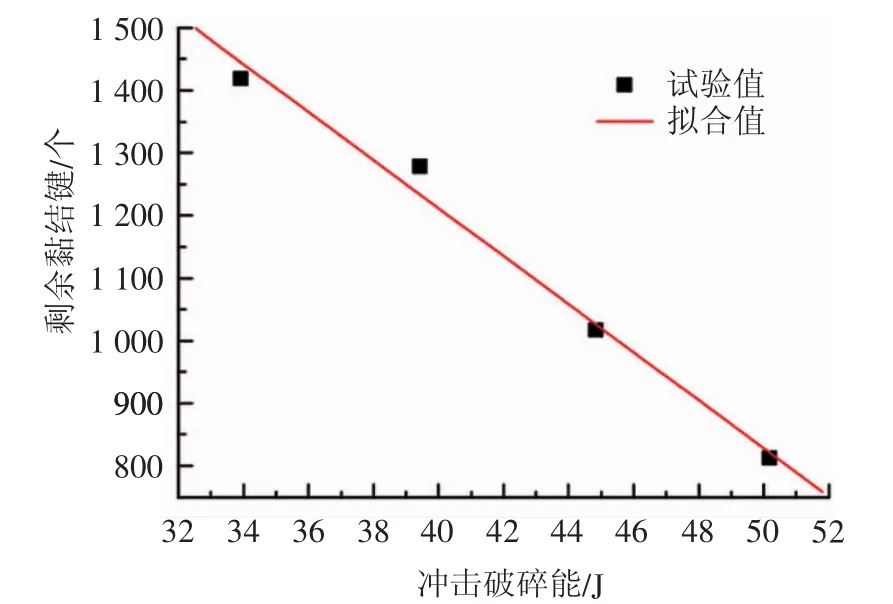
图6冲击破碎能与黏结键数目关系曲线Fig.6 Relationshipcurveofimpactcrushingenergyandbondnumber

从图6可以看出，冲击破碎能与破碎后剩余黏结键数目呈线性关系；通过数据线性拟合得到了冲击破碎能与剩余黏结键的函数关系如式（1）所示，由相关系数R2=0.993可看出线性关系明显。

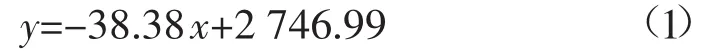
2.4双摆锤冲击破碎力分析

通过EDEM后处理器，可提取不同冲击角下，双摆锤几何体冲击过程中破碎力与时间的关系数据。为了便于分析曲线，根据数据，取摆锤与多尺度内聚颗粒模型相接触时为起始时间点，时间间隔为0.000 5 s，绘制不同冲击角下摆锤破碎力与时间的关系曲线，如图7所示。

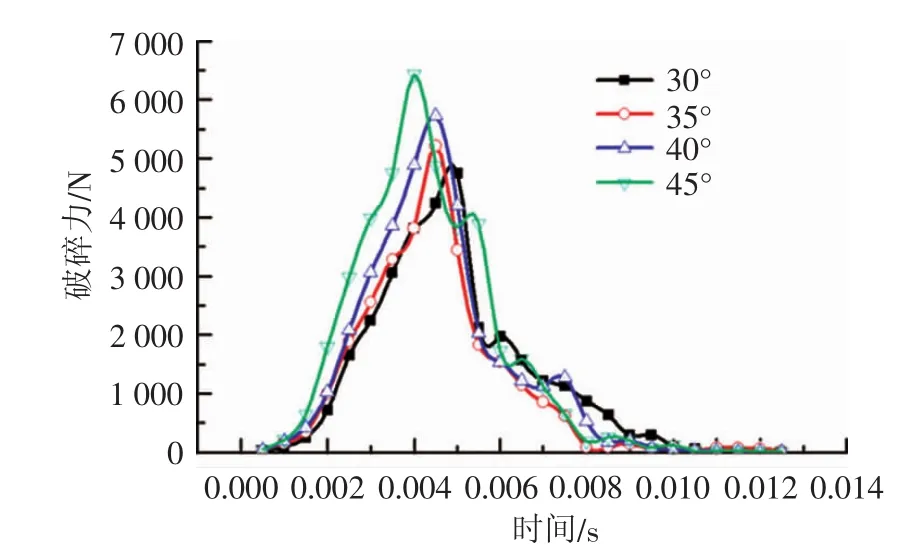
图7摆锤几何体破碎力与时间关系曲线Fig.7 Relationshipcurveofpendulumgeometrycrushingforceandtime

由7图可以看出，矿石在冲击过程中，其摆锤破碎力随着时间增加迅速增大，当达到最大值后开始逐渐减小。对比不同冲击角可以看出，在初始上升阶段，冲击角越大，同一时刻节点处，摆锤作用于矿石上的力也越大，即冲击破碎能越大，几何体作用于矿石的破碎力也越大；下降阶段无较明显规律。为分析最大破碎力与冲击破碎能关系，根据得到的最大破碎力数据，得出最大冲击力与冲击角度之间的关系曲线如图8所示。

由图8可以看出，随着冲击破碎能的增加，摆锤的最大破碎力与冲击破碎能有较好的线性特性。通过线性拟合得到了二者间函数关系如式（2）所示，由相关系数R2=0.994可知，二者具有较好的线性关系。

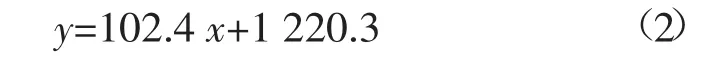
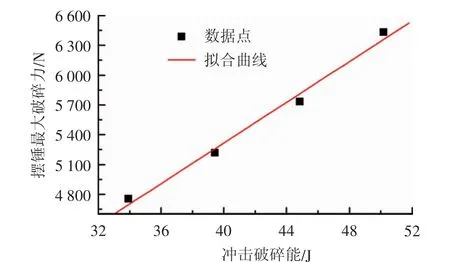
图8冲击破碎能与最大破碎力关系曲线Fig.8 Relationship curve of impact energy and maximum breaking force

3仿真效果与试验结果对比

通过ADAMS与EDEM耦合仿真结果与试验破碎结果对比结果，如图9所示。

图9试验与仿真破碎结果对比Fig.9 Comparison of experimental results and simulation results

3.1冲击破碎效果仿真分析

在EDEM仿真中，粒度分布主要在于获取碎后仍黏结以及未黏结的颗粒集合体在不同粒度筛网上的含量。

为了近似给出其破碎后的粒度分布，通过PROE构建孔径分别为2 mm、5 mm、8 mm、10 mm、12 mm、14 mm的物理筛网，对破碎后的粒度进行筛分。筛网的物理模型如图10所示。

筛分后通过EDEM后处理中Manual Selection确定不同筛网上的每个球颗粒质量，得出各筛网上所占质量分数；从而得到摆锤在35°、40°、45°冲击角下矿石破碎后不同粒度分布概率密度曲线，如图11所示。

从图11可知，随着冲击角度的增加，粗粒含量逐渐减小，中间粒度含量变化较大，而细粒含量变化不大。6 mm以下的颗粒质量分数明显较高，而中间粒度颗粒质量分数相对较小，这可能是由于构建的多尺度内聚颗粒模型外部颗粒黏结不如内部紧密，在外力作用下易碎，也可能是在筛分时，发生了二次碎裂。从曲线图上可以看出，多尺度内聚颗粒模型破碎后粒度分布符合粗颗粒含量较多，呈现出一定的单峰偏度正态特性。

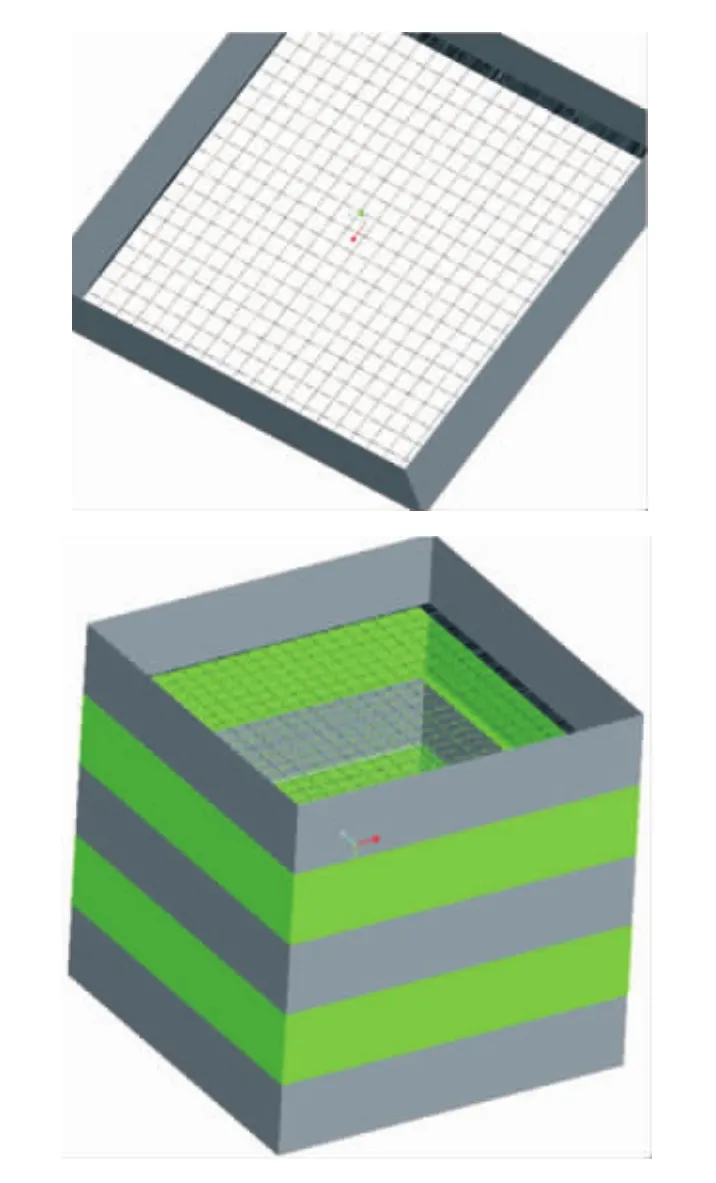
图10筛网物理模型Fig.10 Physical model of the screen

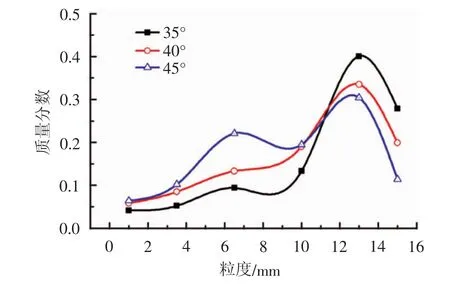
图11不同冲击角仿真破碎粒度分布曲线Fig.11 Brokengrainsizedistributioncurveunderdifferentimpactangles

3.2破碎粒度分布概率密度曲线

将摆锤分别提升至35°、40°、45°，对24 mm粒度钨矿石进行冲击破碎，破碎后结果统计如表3所示。

由表中数据总体上可以看出，冲击破碎后粗料含量占主要，细料含量相对较少；随着冲击破碎角度的提升即冲击破碎能越大，破碎效果越好。对表中数据在MATLAB中进行处理，作出不同冲击角下粒度分布曲线图如图12所示。

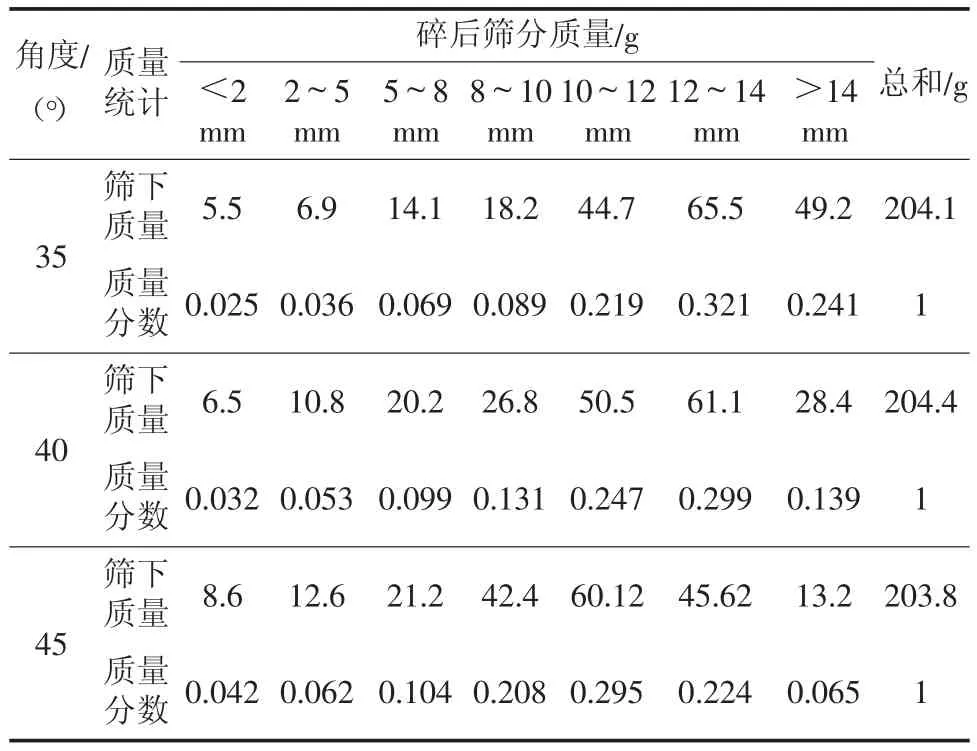
表3不同冲击角时对24mm矿石破碎试验统计结果Tab.3 Orecrushingteststatisticsunderimpactanglesof35,40and45

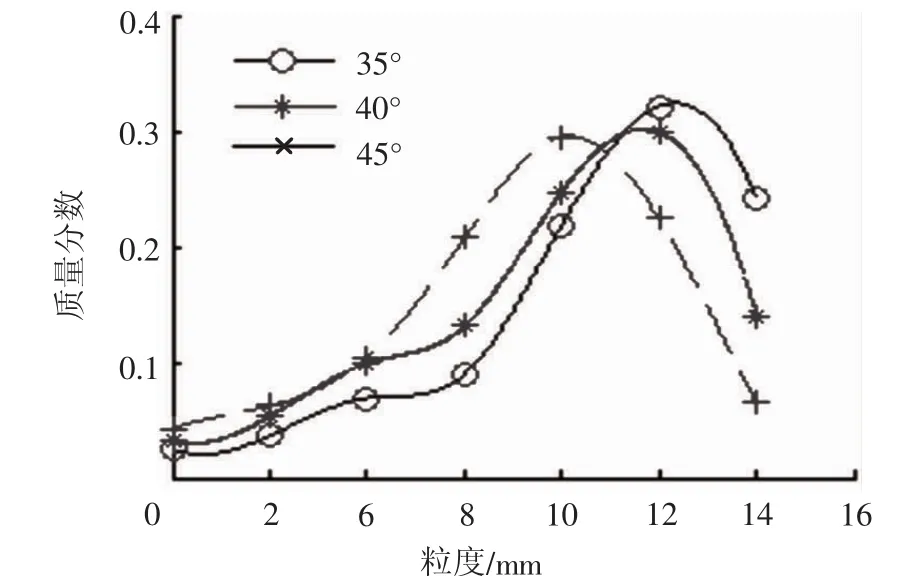
图12 24 mm矿石破碎粒度分布曲线Fig.12 Crushing size distribution curve for 24 mm ore

由图12可以看出，破碎概率密度曲线总体上趋向左偏，即破碎后粗料矿石产量较高；随着冲击破碎能增加，破碎后粗料逐渐减少，中间粒度含量逐渐增加，对于细料区矿石的含量增加相对较慢，破碎后概率密度曲线趋于单峰偏度正态分布。

对比图11与图12，模型破碎后粒度分布情况与实际破碎后粒度分布相近，一致性较好，都具有一定的单峰偏度正态特性。因此采用多尺度内聚颗粒模型通过EDEM与ADAMS耦合模拟矿石冲击破碎是可行的，可以为后续矿石冲击破碎机理的深入研究提供有益指导。

4结论

（1）通过仿真模拟发现，多尺度内聚颗粒模型在冲击破碎过程中具有较明显的弹性变形阶段、塑性变形阶段以及断裂破碎阶段。

（2）随着冲击破碎能的增加，多尺度内聚颗粒模型黏结键断裂越迅速，剩余数目黏结键数目也越少，冲击破碎能与剩余黏结键数目具有一定线性关系。同时随着冲击破碎能增加，多尺度内聚颗粒模型反作用于摆锤的力越大，即摆锤的破碎力也越大，冲击破碎能与最大破碎力之间呈线性关系。

（3）对多尺度内聚颗粒模型破碎结果进行了筛分，碎后的粒度分布概率密度曲线与试验结果对比表明，多尺度内聚颗粒模型破碎后的粒度分布与试验结果一致性较高，因此采用多尺度内聚颗粒模型通过EDEM与ADAMS耦合模拟矿石冲击破碎是可行的，可以在后续研究中加以利用。

参考文献：

[1]张雪颖，阮怀宁，贾彩虹.岩石损伤力学理论研究进展[J].四川建筑科学研究，2010，36（2）：134-138.

ZHANG Xue-ying，RUAN Huai-ning，JIA Cai-hong. Research development of the rock's damage theory [J]. Sichuan Building Science，2010，36（2）：134-138.

[2]任韦波，许金余，刘远飞.高温后玄武岩纤维混凝土冲击破碎分形特征[J].振动与冲击，2014，33（10）：167-171.

REN Wei-bo，XU Jin-yu，LIU Yuan-fei. Fractal characteristics of fragments of basalt fiber reinforced concrete after elevated temperatures under impact loading [J]. Journal of Vibration and Shock，2014，33（10）：167-171.

[3]周博，黄润秋，汪华斌.基于离散元法的砂土破碎演化规律研究[J].岩土力学，2014，35（9）：2710-2716.

ZHOU Bo，HUANG Run -qiu，WANG Hua -bin. Study of evolution of sand crushability based on discrete elements method [J].Rock and Soil Mechanics，2014，35（9）：2710-2716.

[4]徐佩华，黄润秋，邓辉.颗粒离散元法的颗粒碎裂研究进展[J].工程地质学报，2012，20（3）：410-418.

XU Pei-hua，HUANG Run-qiu，DENG Hui.Advances in fractures of particles with distinct element method[J]. Journal of Engineering Geology，2012，20（3）：410-418.

[5]徐永福，奚悦，冯兴波，等.岩石单颗粒压缩破碎的数值模拟分析[J].工程地质学报，2015，23（4）：589-596.

XU Yong-fu，XI Yue，FENG Xing-bo，et al.Simulatio of rock grain breakage using PFC2D[J].Journal of Engineering Geology，2015，23 （4）：589-596.

[6]董爱民，蒋国盛.土体颗粒破裂过程离散元模拟的新方法[J].科学技术与工程，2014，14（25）：277-281.

DONG Ai -ming，JIANG Guo -sheng.New method for DEM simulation of particle crushing evolution in Soil [J].Science Technology and Engineering，2014，14（25）：277-281.

[7] WANG J，YANH B.DEM analysis of energy dissipation incrushable soils[J].Soils and Foundations，2012，52（4）：64-67.

[8]康杰，杨云川.滑石冲击破碎三维数值模拟[J].中国粉体技术，2010，16（2）：68-71.

KANG Jie，YANG Yun -chuan.Three -dimensional numerical simulation of talc impact crushing [J].China Powder Science and Technology，2010，16（2）：68-71.

[9]江红祥，杜长龙，刘送永.冲击速度对煤岩破碎能量和粒度分布的影响[J].煤炭学报，2013，38（4）：604-609.

WANG Hong-xiang，DU Chang-long，LIU Song-yong.The effects of impact velocity on energy and size distribution of rock crushing [J]Journal of China Coal Society，2013，38（4）：604-609.

[10]李洪昌，李耀明，唐忠，等.基于EDEM的振动筛分数值模拟与分析[J].农业工程学报，2011，27（5）：117-121.

LI Hong -chang，LI Yao -ming，TANG Zhong，et al.Numerical simulation and analysis of vibration screening based on EDEM[J]. Transactions of the Chinese Society of Agricultural Engineering，2011，27（5）：117-121.

Simulation Analysis of Impact Crushing based on EDEM and ADAMS Coupling

LIU Zhi-gang, CAI Gai-pin, ZENG Yan-xiang, LU Xiao-jiang, YU Shi-ke
(School of Mechanical & Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China)

Abstract:Multi-scale cohesive particles can demonstrate obvious stages of elastic deformation, plastic deformation and fracture crushing by impact crushing simulation. This paper conducted impact crushing simulation experiments on tungsten ore's multi -scale cohesive particle model established by discrete element method by EDEM and ADAMS bidirectional coupling. The changing curves of broken adhesive bonds, impact crushing force with the variation of time under different impact angles were analyzed, which showed that the broken adhesive bonds and impact crushing force showed a linear relationship. The post-crushing particle size distribution of the multi-scale cohesive particle model has the single peak skewness normal characteristics by screening and statistical analysis. The comparison of experimental results and simulation results showed the favorable feasibility of impact crushing based on EDEM and ADAMS Coupling.

Key words:bidirectional coupling; discrete element method; multi-scale; impact grinding

通讯作者：蔡改贫（1964-），男，江西赣州人，教授，博士，主要从事近净成形新技术、物料高效破碎进技术研究与装备开发。

作者简介：刘志刚（1989-），男，山西太原人，硕士研究生，主要研究方向为矿山机械—散体系统。

收稿日期：2015-11-11

DOI：10.3969/j.issn.1009－0622.2016.01.014

中图分类号：TQ172.6+1；TP15

文献标识码：A

资助项目：国家自然科学基金项目（51464017）；江西省高等学校科技落地计划项目（KJLD13045）