存在复杂非均匀层的一维大地电磁正演

凌嘉宣，李长伟，赵荣春，熊 彬

(桂林理工大学地球科学学院，广西桂林 541004)

存在复杂非均匀层的一维大地电磁正演

凌嘉宣，李长伟，赵荣春，熊 彬

(桂林理工大学地球科学学院，广西桂林 541004)

二、三维大地电磁(MT)正反演常采用一维反演结果作为初始迭代模型或利用一维模型响应定义边界条件，为进一步研究复杂地层条件下的MT响应，本文推导了非均匀层电导率随深度按线性－指数函数变化和指数－线性函数变化的一维MT正演的解析解形式，在此基础上对不同的地层组合情况进行讨论，分析了非均匀层埋深、厚度对MT响应的影响，并与地下介质均匀以及非均匀层电导率随深度按单一函数变化的MT响应进行对比。结果表明，既存在线性变化又存在指数变化的介质模型MT响应远比单一变化介质模型复杂，随着过渡层厚度增大、埋深变浅，其视电阻率和相位幅值与均匀介质模型响应幅值差异变大。

大地电磁测深;非均匀层;正演

近年来，国内外学者对大地电磁正反演开展了广泛的研究，在二、三维正反演中，通常利用一维正演响应定义边界条件或作为背景场响应，取一维反演结果作为反演的初始迭代模型［1－3］。在通常的一维MT正演中，取层状地球各层介质的电导率为定值，然而在实际情况中地层电阻率可能是随深度变化的。文献［4－10］对电导率随深度按线性函数变化的地球模型进行了研究;文献［11－12］对电导率随深度按指数函数变化的地球模型进行了分析;文献 ［13－16］对电导率随深度分层线性变化的模型进行了探讨;文献 ［17－20］对电导率分块变化模型进行了研究，但仅对非均匀层电导率按单一变化(线性变化或指数变化)进行研究，在实际工作中岩矿石因组成、湿度、温度、孔隙度及渗透性的变化，其电导率可能存在多种形式的变化。本文对局部介质中同时存在电导率随深度按线性变化和指数变化的非均匀层复杂模型进行研究，从理论上分别推导过渡层电导率先按线性变化后按指数变化(conductivity first vary linearly then exponentially with depth，CFVLTE)及先按指数变化后按线性变化(conductivity first vary exponentially then linearly with depth，CFVETL)4层(第2、3层为非均匀层)大地模型视电阻率的表达式，并在此基础上对CFVETL模型进行大地电磁正演研究，分析了过渡层厚度、埋深等对水平层状介质的视电阻率和相位曲线的影响，进一步充实复杂介质一维大地电磁基本理论。

1 存在非均匀层状介质正演理论

下面分别对非均匀层电导率随深度按线性－指数函数变化模型(CFVLTE模型)及按指数－线性函数变化模型(CFVETL模型)进行分析。

1.1 非均匀层电导率随深度按线性－指数函数变化理论

设4层地球模型(图1a)，选用笛卡尔右手坐标系，x、y轴在地表水平面内，z轴铅锤向下，电导率变化如图1b所示，第1、4层为均匀介质，其电导率为常量，分别为σ1、σ4;第2和第3层皆为非均质层，其中第2层电导率σ2随深度呈线性变化，从σ1变至σ2'(σ2'为第2层底界面电导率，与第3层顶界面电导率相等)，而第3层电导率σ3随深度呈指数变化，从σ2'变至σ4(非均匀层电导率变化如图1b所示)，即:

图1 非均匀层按线性－指数函数变化的层状介质模型(a)及电导率变化示意图(b)Fig.1 Model(a)and conductivity vary(b)of CFVLTE for inhomogeneous layer

对于第2层，

其中α定义为

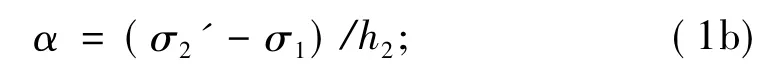
对于第3层，

其中p定义为

α和p为电导率的变化率，其正负号值取决于电导率随深度的变化，正号表示电导率随深度增大而增加。

根据卡尼尔、吉洪诺夫经典理论，假设场源为垂直入射的平面波，极化方向沿x轴，时谐因子取eiωt。于是在各层中描述电场水平分量Ex的微分方程式为［7］

式中:ω为角频率;μ为介质磁导率;σ(z)为介质电导率。非均匀层以外的其他地层电场水平分量Ex和磁场水平分量Hy表达式分别为［7］

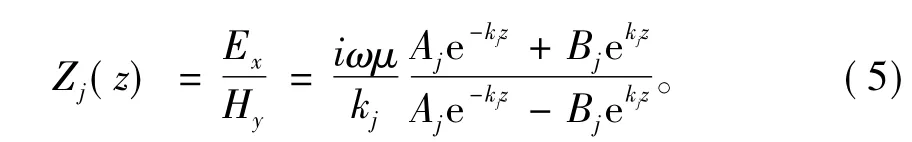
对于电导率随深度呈线性变化的第2层，式(3)取如下形式

令

则有

将式(7)中第2个等式对z求导并代入式(6)中，整理后得到

式(8)为Airy微分方程式，其解为

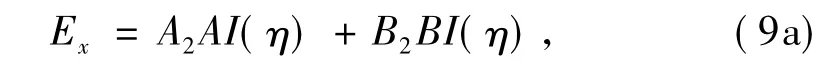
其中:A2、B2为需利用边界条件确定的系数;AI、BI分别为第一类和第二类Airy函数。水平磁场分量为

式中:AI'(η)和BI'(η)表示相对η的导数。

对于电导率随深度呈指数变化的第3层，式(3)取如下形式:

其中，k2'2=iωμσ2'。令

则有

将式(12)中第2个等式对z求导并代入式(10)中，整理后得

等式(13)为修正贝塞尔方程，其解为

式中:K0和I0为修正贝塞尔函数;A3和B3为需利用边界条件确定的系数。

利用关系式K0'(q)=－K1(q)及 I0'(q) = I1(q)，得到磁场水平分量Hy为

因电场和磁场切向分量的连续性，则其比值波阻抗也连续，故在各边界(zj=z1，z2，z3)上满足

式中:η1=(iωμ/α2)1/3σ1;η2=(iωμ/α2)1/3σ2';q2=2k2'/p;q3=2k4/p;θ=k2'。解上面各等式，并令Rj=Bj/Aj，获得

在式(5)中取j=1，z=0，得到地面阻抗表达式为

视电阻率和阻抗相位分别为

根据式(18a)～(18c)及式(19)～(21)即可计算出非均匀层先按线性变化后按指数变化的视电阻率和相位。

若非均匀层上不存在覆盖层，则h1=0，进而由式(18a)可得R1=0，此时σ1表示非均匀层顶部的电导率，地面阻抗公式变为

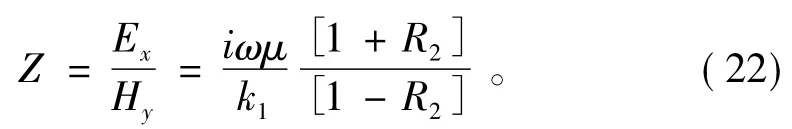
根据式(18b)、(18c)、(20)～(22)可计算出非均匀层上不存在覆盖层时的视电阻率和相位的值。

1.2 非均匀层电导率随深度按指数－线性变化理论

此时4层地球模型如图2a所示，电导率变化如图2b所示，第1、4层为均匀介质，第2层电导率σ2随深度呈指数变化，第3层电导率σ3随深度呈线性变化，即:

对于第2层，

及

对于第3层，

及

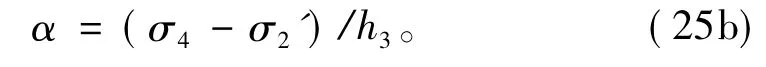
对于电导率随深度呈指数变化的第2层，电场和磁场水平分量分别为

电导率随深度呈线性变化的第3层电场和磁场水平分量分别为

图2 非均匀层按指数－线性函数变化的层状介质模型(a)及电导率变化示意图(b)Fig.2 Model(a)and conductivity vary(b)of CFVETL for inhomogeneous layer

根据式(31a)～(31c)及式(19)～(21)即可计算出非均匀层先按指数变化后按线性变化的视电阻率和相位。

若非均匀层上不存在覆盖层，则h1=0，R1= 0，根据式(31b)、(31c)、(20)～(22)可计算出非均匀层上不存在覆盖层时的视电阻率和相位的值。

2 存在非均匀层介质的模型算例与分析

非均匀介质的4层模型根据第2层底面电阻率的不同取值，可分为以下几种情况:CFVLTE (CFVETL)模型下基底为高阻时可分为非均匀层电阻率先按线性(指数)增大后按指数(线性)减小、先按线性(指数)增大后按指数(线性)增大和先按线性(指数)减小后按指数(线性)增大3种情况; CFVLTE(CFVETL)模型下基底为低阻时可分为非均匀层电阻率先按线性(指数)增大后按指数(线性)减小、先按线性(指数)减小后按指数(线性)增大和先按线性(指数)减小后按指数(线性)减小3种情况。

在文献［12］中，Kao计算了第2层电导率为指数变化的3层介质模型的大地电磁响应，为作对比，本文选用相同的模型与参数进行计算，结果见图3。可以看出，两者计算结果高度吻合，说明本文算法的正确性。

2.1 第2层底界面电阻率 ρ2'不同取值时的大地电磁响应

为了能更好的反映出深部大地结构信息，取频率范围为10－20～104Hz。图4～7为CFVLTE模型和CFVETL模型下基底为高阻和低阻时对应的视电阻率和相位响应曲线图，其中模型参数h1= 100 m，h2=h3=50 000 m，ρ1=10Ωm，基底为高阻时ρ4=104Ωm，基底为低阻时ρ4=10－4Ωm，两个模型的第2层底界面电阻率 ρ2'分别取不同的值。第2层底部电阻率ρ2'=101Ωm时与第1层电阻率相等，故第1、2层可看作一均匀层，CFVLTE模型下表示非均匀层按指数变化的3层模型，CFVETL模型下则为非均匀层按线性变化的3层模型。基底为高阻时，第2层底部电阻率 ρ2'=104Ωm时与第4层电阻率相等，故第3、4层可看作一均匀层(基底为低阻，第2层底部电阻率ρ2'=10－4Ωm时，第3、4层可看作一均匀层)，CFVLTE模型和CFVETL模型下分别表示非均匀层按线性变化和指数性变化的3层模型。从图4～7可看出无论在CFVLTE模型或CFVETL模型下，第2层底部电阻率变化情况相同时，视电阻率和相位响应曲线变化形状相似。而非均匀层电阻率按线性变化的曲线比按指数变化的曲线的差异要大，这说明了基底无论是高阻或低阻，非均匀层中按线性变化层与按指数变化层厚度相等时，线性变化层对视电阻率和相位的影响远大于指数变化层对视电阻率和相位的响应值。

图3 非均匀层电阻率按指数变化模型的大地电磁测深曲线Fig.3 Magnetotelluric sounding curves of CFVLTEmodel

非均匀层电导率的变化率α和p对视电阻率和相位响应的影响与第2层底部电阻率ρ2'对视电阻率和相位响应的影响情况相似，故不再赘述。

图4 CFVLTE模型下基底为高阻时第2层底部电阻率变化的视电阻率(a)和相位(b)曲线图Fig.4 Apparent resistivity(a)and phase(b)curves of CFVLTEmodel of second layer bottom with varying resistivity in a high resistance substratum

图5 CFVLTE模型下基底为低阻时第2层底部电阻率变化的视电阻率(a)和相位(b)曲线图Fig.5 Apparent resistivity(a)and phase(b)curves of CFVLTEmodel of second layer bottom with varying resistivity in a low resistance substratum

图6 CFVETL模型下基底为高阻时第2层底部电阻率变化的视电阻率(a)和相位(b)曲线图Fig.6 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of second layer bottom with varying resistivity in a high resistance substratum

图7 CFVETL模型下基底为低阻时第2层底部电阻率变化的视电阻率(a)和相位(b)曲线图Fig.7 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of second layer bottom with varying resistivity in a low resistance substratum

由上面分析可知，第2层底部电阻率变化时，CFVLTE模型与CFVETL模型的大地电磁响应视电阻率和相位的变化情况相似，故下面仅对CVETL模型下的情况与非均匀层电导率按其他方式变化的情况之间的关系进行分析。设电阻率按线性变化3层模型(第2层为非均匀层，Linear模型)和按指数变化3层模型(第2层为非均匀层，Exponential模型)基底为高阻时的参数为ρ1=10Ωm，ρ4=104Ωm(基底为低阻时ρ4=10－4Ωm)，h1=100 m，h2/h1=103;不存在非均匀层的2层模型(Cagnirad模型)参数为ρ1=10Ωm，ρ2=104Ωm(基底为低阻时ρ4=10－4Ωm)。将以上模型与ρ2'取不同值的4层模型对比，基底为高阻时ρ2'取105、102和10－2Ωm分别表示非均匀层先按指数增加后按线性减小、先按指数增大后按线性增大和先按指数减小后按线性增大的情况;基底为低阻时ρ2'取102、10－2和10－5Ωm，即表示非均匀层先按指数增加后按线性减小、先按指数减小后按线性减小和先按指数减小后按线性增大的情况，响应视电阻率和相位曲线如图8～9所示。由图8可知:基底为高阻时由于非均匀层的存在导致相应的电阻率响应与地下为均匀介质情况下的电阻率和相位响应有差异，非均匀层按指数增加后按线性变化的模型与非均匀层仅按线性变化或指数变化的模型的视电阻率和相位曲线形状相似，并在均质情况下电阻率和相位曲线向右移动。非均匀层按指数减小后按线性增加的模型的响应视电阻率曲线同时向下和向右移动，曲线能较好地反映出非均匀层电阻率的变化趋势。由图9可知:第2层基底电阻率越小，视电阻率曲线越向下移动并能明显反映非均匀层电阻率的变化趋势。通过分析可知同时存在线性变化和指数变化的非均匀层模型远远比仅按线性或指数变化的模型对视电阻率和相位的响应复杂。

图8 CFVETL模型下基底为高阻时第2层底部电阻率ρ2'、Cagnirad模型、Linear模型及Exponential模型响应的视电阻率(a)和相位(b)曲线图Fig.8 Apparent resistivity(a)and phase(b)curves of CFVETLmodel，Cagnirad model，Linearmodel and Exponentialmodel in high resistance substratum

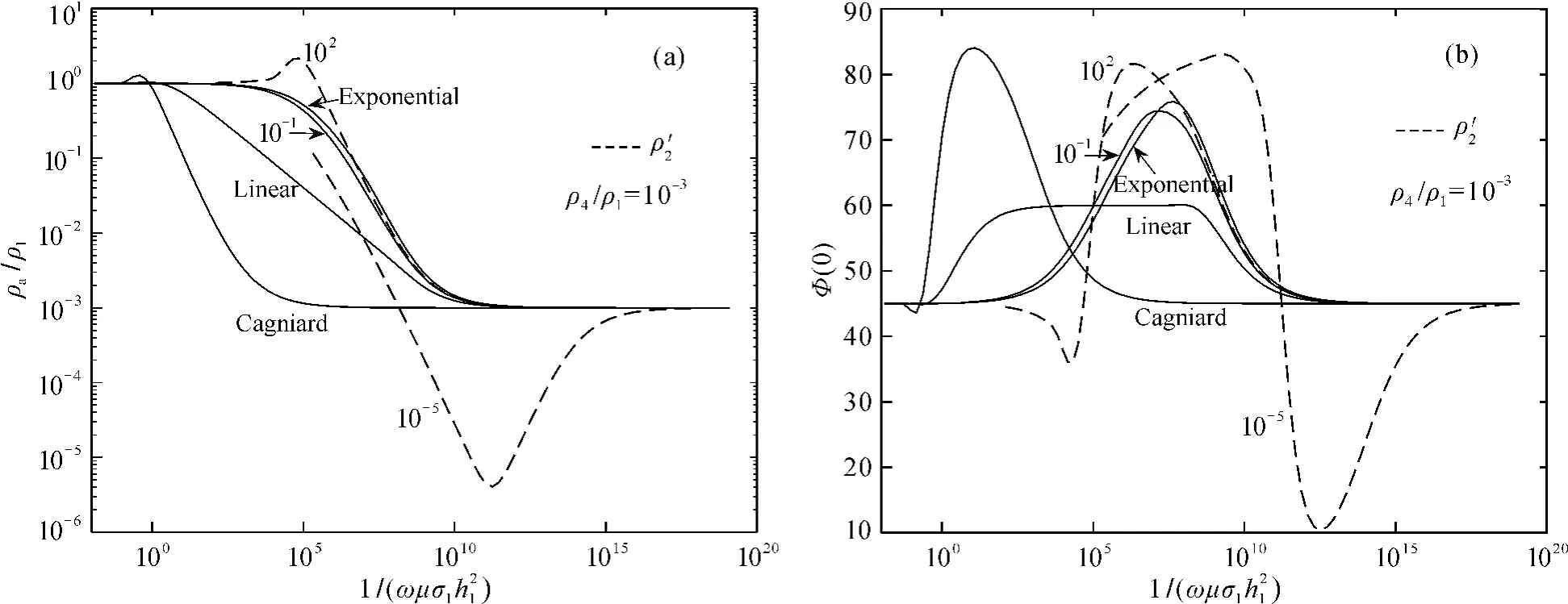
图9 CFVETL模型下基底为低阻时第2层底部电阻率ρ2'变化、Cagnirad模型、Linear模型及Exponential模型响应的视电阻率(a)和相位(b)曲线图Fig.9 Apparent resistivity(a)and phase(b)curves of CFVETLmodel，Cagnirad model，Linearmodel and Exponentialmodel in low resistance substratum

2.2 非均匀层厚度变化对大地电磁响应的影响

限于篇幅，本文仅给出CFVETL模型下基底为高阻非均匀层电阻率按指数增加后按线性增加和基底为低阻时电阻率按指数减小后按线性减小的两种情况，图10和图11分别为两种情况下非均匀层厚度h23/h1(h23=h2+h3，h2=h3=h23/2)取不同的值相应的视电阻率和相位响应曲线。其中第1层电阻率和厚度分别为10Ωm和100 m，0曲线表示不存在过渡层时的均匀介质。由图分析可知，因非均匀层的存在导致响应的视电阻率和相位与地下均匀介质情况下的视电阻率和相位有差异，并能反映出非均匀层电阻率的变化，当非均匀层的厚度越薄时，其对应的视电阻率和相位响应值越接近均匀介质情况下的响应值;当非均匀层越厚时，其异常值与均匀介质下的响应值差异越大。

图10 CFVETL模型下基底为高阻时非均匀层电阻率按指数增大后按线性增大的模型厚度变化视电阻率(a)和相位(b)曲线图Fig.10 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of inhomogeneous layer thickness varying in high resistance substratum with inhomogeneous layer resistivity first increase exponentially then increase linearly with depth

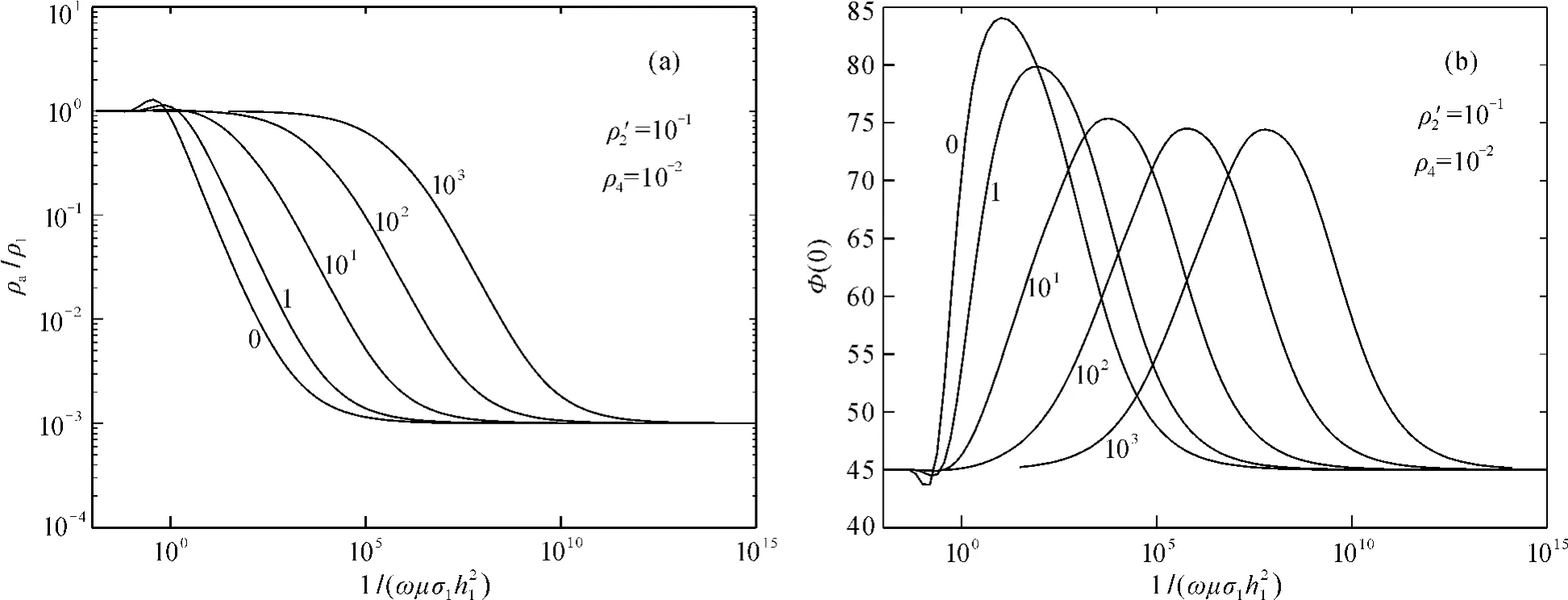
图11 CFVETL模型下基底为低阻时非均匀层电阻率按指数减小后按线性减小的模型厚度变化视电阻率(a)和相位(b)曲线图Fig.11 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of inhomogeneous layer thickness varying in low resistance substratum with inhomogeneous layer resistivity first decrease exponentially then decrease linearly with depth

2.3 非均匀层电阻率变化对大地电磁响应的影响

CFVETL模型下基底为高阻时非均匀层电阻率按指数增加后再按线性增加和基底为低阻时电阻率按指数减小后按线性减小的两种情况下，探讨非均匀层埋深对视电阻率和相位响应的影响。图12和图13分别为非均匀层埋深对视电阻率和相位响应曲线图，0曲线表示非均匀层上无覆盖层的响应，Cagniard 2层模型第1层厚度为103m。可知，无论基底为高阻或低阻，由于非均匀层的存在，导致相应的电阻率响应与地下均匀层介质的情况下的电阻率响应有差异，非均匀层埋深越小，其相应的视电阻率响应值与均匀介质情况下的视电阻率响应值差异越大。当非均匀层的埋深越大，异常值与均匀介质情况下的视电阻率响应值差异越小。

图12 CFVETL模型下基底为高阻时非均匀层电阻率按指数增大后按线性增大的模型埋深变化视电阻率(a)和相位(b)曲线图Fig.12 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of inhomogeneous layer buried depth varying in high resistance substratum with inhomogeneous layer resistivity first increase exponentially then increase linearly with depth

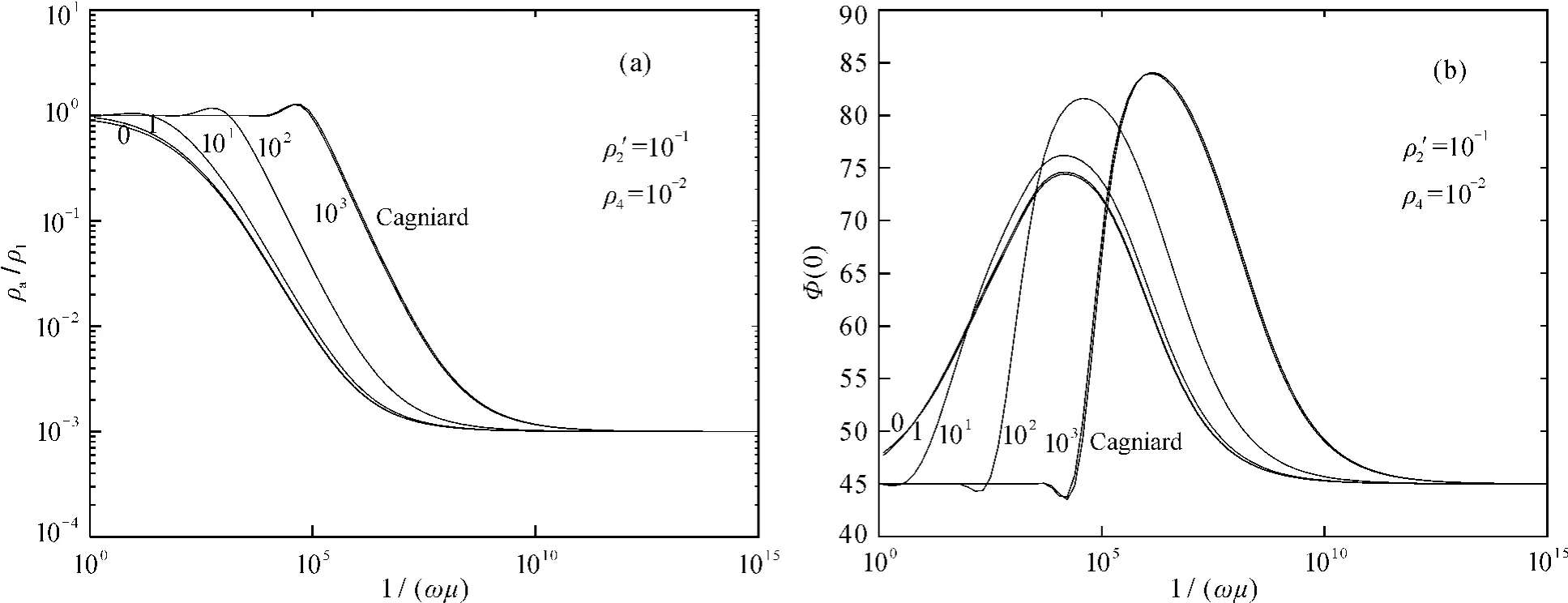
图13 CFVETL模型下基底为低阻时非均匀层电阻率按指数减小后按线性减小的模型埋深变化视电阻率(a)和相位(b)曲线图Fig.13 Apparent resistivity(a)and phase(b)curves of CFVETLmodel of inhomogeneous layer buried depth varying in low resistance substratum with inhomogeneous layer resistivity first decrease exponentially then decrease linearly with depth

3 结论

本文提出的CFVLTE模型和CFVETL模型更真实模拟野外的实际情况，推导出的一维MT正演的解析解形式与前人计算结果对比，验证了本文程序的正确性;对非均匀层中第2层底部电阻率变化模型进行正演计算及与电导率单一变化模型正演对比说明了非均匀层电导率非单一变化介质的复杂性;对CVETL模型下非均匀层埋深、厚度分析有助于对大地电磁测深资料进一步的补充。本文只是考虑了各向同性介质情况，对各向异性介质电导率非单一变化的方法有待进一步研究。

［1］Newman G A，Alumbaugh D L．Three-dimensional magnetotelluric inversion using non-linear conjugate gradients［J］．Geophysical Journal International，2000，140(2):410－424．

［2］Ren ZY，Kalscheuer T，Greenhalgh S，etal．A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modeling［J］．Geophysical Journal International，2013，194(2):700－718．

［3］Cai H Z，Xiong B，and Han M R，et al．3D controlled-source electromagnetic modeling in anisotropic medium using edgebased finite elementmethod［J］．Computers＆Geosciences，2014，73:164－176．

［4］Wait JR．Electromagnetic Waves in Stratified Media［M］．Oxford:Pergamon Press，1962．

［5］Mallick K．Magnetotelluric sounding on a layered earth with transitional boundary［J］．Geophysical Prospecting，1970，18(S1):738－757．

［6］Abramovici F．The forward magnetotelluric problem of an inhomogenous and anisotropic structure［J］．Geophysics，1974，39(1):56－68．

［7］Kao D，Rankin D．Magnetotelluric response on inhomogeneous layered earth［J］．Geophysics，1980，45(12):1793－1802．

［8］Kao D．Magnetotelluric response on vertically inhomogeneous earth having conductivity varying linearlywith depth［J］．Geophysical Prospecting，1982，30(6):866－878．

［9］陈乐寿，王光锷．大地电磁测深法［M］．北京:地质出版社，1990:36－48．

［10］欧东新，阮百尧，王家林．电导率线性变化测井二维有限单元法数值模拟［J］．同济大学学报，2005，33(5): 692－695．

［11］Berdichevskiy M I，Dmitriyev V I，Mershchikova N A．Investigation of gradientmedia in deep electromagnetic sounding［J］．Physics of the Solid Earth，1974，6:380－386．

［12］Kao D．Magnetotelluric response on vertically inhomogeneous earth having conductivity varying exponentially with depth［J］．Geophysics，1982，47(1):89－99．

［13］徐世浙．电导率分段线性变化的水平层的点电源电场的数值解［J］．地球物理学报，1986，29(1):84－90．

［14］方胜，罗延钟．电导率随深度分层线性变化的大地电磁响应［J］．地球物理学报，1991，34(2):216－227．

［15］方胜，罗延钟．导电率随深度分层线性变化的一维大地电磁正、反演问题的研究［J］．地球科学——中国地质大学学报，1990(S):86，96．

［16］徐世浙，刘斌．电导率分层连续变化的水平层的大地电磁正演［J］．地球物理学报，1995，38(2):262－268．

［17］阮百尧，徐世浙．电导率分层线性变化二维地电断面电阻率测深有限元数值模拟［J］．地球科学——中国地质大学学报，1998，23(3):303－307．

［18］戴前伟，张富强，杨坤平，等．电导率分块线性变化的二维高频大地电磁法有限元正演模拟［J］．物探化探计算技术，2012，34(5):552－558．

［19］刘云，王绪本．电性参数分块连续变化二维MT有限元数值模拟［J］．地球物理学报，2012，55(6):2079－2086．

［20］欧东新，韦者良．复杂地形电导率线性变化二维大地电磁有限单元法正演模拟［J］．桂林理工大学学报，2014，34(1):30－38．

1D magnetotelluric forward modeling of com plex inhomogeneous layers

LING Jia-xuan，LIChang-wei，ZHAO Rong-chun，XIONG Bin
(College of Earth Sciences，Guilin University of Technology，Guilin 541004，China)

In 2D and 3Dmagnetotelluric(MT)inversion，1D inversion data is often used as the initial iterative model or forward modeling to definite the boundary condition．In order to further study MT response under complex stratum condition，the analytical solution for 1D MTmodeling is derived where the conductivity of inhomogeneous layers vary with depth are linear-exponential and exponential-linear form．On this basis，the differentstratum combination conditions are discussed，and the effect of depth and thickness of inhomogeneous layer on the MT response is analyzed．The results are compared with analytic solution from homogeneousmedium model and single variationmodel．It is shown that the MT responses of linear-and-exponential variationmodelwith inhomogeneous aremore complex than single variation model．With the thickness being larger and the embedded depth being shallower for inhomogeneous layers，the differences of resistivity and phase of MT responsewith the homogeneousmedium model become larger．

magnetotelluric sounding;inhomogeneous layer;forward modeling

P631

:A

2015－10－05

国家自然科学基金项目 (41464002;41674075);广西自然科学基金项目 (2013GXNSFAA019277);广西高校科研项目 (2013YB107)

凌嘉宣 (1989—)，男，硕士研究生，研究方向:应用地球物理，lingjiaxuanyx@foxmail.com。

李长伟，博士，副教授，lcw@glut.edu.cn。

凌嘉宣，李长伟，赵荣春，等．存在复杂非均匀层的一维大地电磁正演 ［J］．桂林理工大学学报，2016，36 (4):660－669．

1674－9057(2016)04－0660－10

10.3969/j．issn.1674－9057.2016.04.004