爆破振动持时分析及微差爆破延期时间优选*
2016-04-17钟冬望
钟冬望,何 理,操 鹏,张 奎
(1.武汉科技大学理学院,湖北 武汉 430065;2.中铁港航-武科大爆破技术研究中心,湖北 武汉 430065;3.湖北皓昇爆破工程有限公司,湖北 十堰 442012)
爆破振动持时分析及微差爆破延期时间优选*
钟冬望1,2,何 理1,2,操 鹏2,张 奎3
(1.武汉科技大学理学院,湖北 武汉 430065;2.中铁港航-武科大爆破技术研究中心,湖北 武汉 430065;3.湖北皓昇爆破工程有限公司,湖北 十堰 442012)
爆破振动持续时间以及微差爆破延期时间分别是爆破振动危害客观评价与主动控制的重要指标,对振动持时影响因素和延期时间优选方法进行深入探究极为必要。结合量纲分析理论,探讨了爆破振动持时影响因素,推导出爆破振动持时预测公式,该公式线性相关性达到89.7%;基于地震波线性叠加原理,通过MATLAB 7.0编程,计算得到毫秒微差爆破不同爆心距处合理延时区间。结果表明,爆破振动信号能量与振动持续时间相关性高,在振动持时预测公式中引入信号能量,可提高预测精度;振动持续时间与比例速度负相关,与比例药量正相关;合理孔间延期时间往往不是某一具体值,而是一个或多个时间区间;不同爆心距处合理延期时间值不同。工程应用表明,给出的爆破振动持时预测公式与微差爆破延时优选方法切实可行。
爆炸力学;振动持续时间;量纲分析;延期时间;线性叠加原理;微差爆破
爆破振动危害的准确预测及有效控制是工程爆破领域有待深入研究的重大难题之一[1-6]。随着爆破技术与民众安全意识的提高,很多国家均制定了振动速度与频率相结合的爆破振动安全标准,使得爆破振动安全评价体系更加科学化、合理化[7-9],但大量工程实践表明爆破振动作用下,建(构)筑物的受损程度与爆破振动信号所携带能量的相关性较高[10-12],且能量又由振动速度、频率与振动持续时间综合表征[13],较长的爆破振动持续时间造成的振动累积、疲劳效应不容忽视,而现行的爆破安全标准未将爆破振动持续时间考虑在内,故进一步对爆破振动持续时间进行相关理论研究与探讨极为必要。在充分研究爆破振动效应的同时,若能提出有效降低爆破振动危害的主动控制措施,才能顺利开展生产、进一步推动爆破技术的发展。
本文中结合单段爆破振动波形特性,基于量纲分析理论,类比天然地震振动持时经验公式,推导爆破振动持时预测公式;基于地震波线性叠加理论,采用MATLAB 7.0对微差爆破延期时间进行优选,总结规律,以期进一步完善爆破振动危害预测方法,实现爆破振动危害的高效、主动控制。
1 爆破振动持时预测方法
1.1 爆破振动持时的量纲理论
爆破振动持续时间对结构的危害主要表现为:当结构反应超越材料弹性极限时,发生强度降低、丧失现象,具体表现为[4]:
(1)对于线性体系,持续的强震使得结构反应出现极值的概率增加;
(2)对于无退化的非线性体系,振动持时的增加使得结构出现较大永久变形的概率增加;
(3)振动持时越长,地震波破坏能量就越大,资料表明[4,8,14],振动持时由1 s增加到50 s,破坏能力平均增大约40倍。
因此,探讨爆破振动持时的影响因素对爆破振动安全判据的研究具有重大理论价值和现实意义。
McGuire主张[15],天然地震的振动持时Td可表示为:
InTd=0.19+1.15M+0.35Inr+0.73Js
(1)
式中:M为地震等级,与爆源能量正相关;r为传播距离;Js为代表介质传播性质的的参数,Js=0代表基岩,Js=1代表土层。
由此可见,天然地震的振动持时主要受地震等级、传播距离以及传播介质性质等因素的影响。
爆破振动与天然地震的区别主要是震源位置及震源能量的差异,它们的传播机理是一致的。类比式(1),可以认定爆破振动持时T是与振动信号携带能量Es、爆心距R、传播介质性质(弹性模量E、泊松比μ)、单响最大药量Q有关的参量。文献[16]中认为,爆破振动是介质弹性和惯性综合作用的结果,
在各向同性的弹性介质中,介质弹性可用弹性模量E和泊松比μ来表征;对于介质的惯性通常用密度ρ来表征。故选取信号携带能量Es(J)、爆心距R(m)、介质弹性模量E(Pa)、介质泊松比μ、介质密度ρ(kg/m3)及单响最大药量Q(kg)作为制约爆破振动持时的主要变量,文中装药结构统一为耦合装药形式。各变量的量纲如表1所示。

表1 各变量的量纲Table 1 Dimension of variables
各变量间的函数关系可表示为:
T=F(Es,E,ρ,R,μ,Q)
(2)
式中:变量数为7,基本量纲数为3,选择独立变量个数为为3,独立变量依次为ρ、R、E,建立4个量纲为一的参量π1、π2、π3、π4,其表达式为:
(3)
由此可以得到:
(4)
在一次爆破作业中,传播介质E、ρ、μ均可视为常数,故对式(3)进行简化,得到:
T/R=F[Es,(Q/R3)]
(5)
因此,一定爆心距范围内,爆破振动持续时间的相似准数方程可写为:
(6)
参照萨道夫斯基公式,对式(6)做乘积变换处理,得到
(7)
式中:Vmax为质点振动峰值速度(cm/s);K1、K2为修正系数;α、β和γ为振动持时跃变指数。
定义Vmax/R、Q1/3/R分别为比例速度和比例药量,比例速度反映了峰值速度随传播距离的变化规律。在单次特定爆破条件下,随传播距离(R)的变化,比例速度与比例药量均出现不同的变化,因此爆破振动持时(T)是比例速度和比例药量综合作用的结果。同时爆破振动持时(T)受地质状况影响很大,同一次爆破中,相同爆心距处,质点振动峰值速度也可能存在较大差异,而式(7)中修正系数K2类似于萨道夫斯基公式中与地震波传播地段介质性质及药包结构特征相关的经验系数K,且式(7)与萨氏公式近似的计算形式恰恰能间接反映出多种因素对振动持时的影响,能大大提高对爆破振动持时的预测精度。大规模微差爆破中,延期时间过短,分段振波主振相会产生干扰叠加现象,导致爆破振动峰值速度与单响最大药量相关性差,式(7)中引入振动信号携带能量(Es)较好的弥补了振动持时的这一预测缺陷,一定微差段数范围内,分段振波间叠加干扰情况愈严重,式(7)中振动信号携带能量(Es)对振动持时预测精度的贡献就愈大。
1.2 爆破振动持时预测公式的工程应用
1.2.1 应用步骤
(1) 根据爆区实地环境状况,针对某次爆破,布置尽可能多的振动监测点,进行爆破振动监测;
(2) 通过统计、处理爆破振动数据依次得到持时预测公式(7)中各参量(T、Vmax、R,Es及Q);
(3) 采用最小二乘法拟合数据,进行线性回归得到持时预测公式中的K2、α、β,确保公式线性拟合相关系数大于81%,否则重复步骤(1)~(3),直至达到拟合要求;
(4) 借助振动监测,应用式(7)对特定点进行爆破振动持时预测。
1.2.2 工程应用实例
在十堰堰口采石场进行单孔爆破试验,单孔耦合装药量为40 kg,主爆药选用岩石膨化硝铵炸药,折合TNT当量35.6 kg[17],选用2#岩石乳化炸药为起爆药。选用成都泰测科技研发的Mini-Blast Ⅰ型爆破振动测试仪进行爆破振动监测,现场测得不同爆心距处爆破振动时程曲线如图1所示,其中V为爆破振动峰值速度。
将爆破振动时程曲线分为主振段与尾振段2个部分,初始波至波幅衰减为最大幅值1/e间的波形为主振段,主振段相应的持续时间为爆破振动持续时间[4]。爆破振动数据如表2所示,其中:信号携带能量Es为通过选取db8小波基,对各信号分别进行深度为11层的小波包分解计算得到[13]。
由表2可以看出,爆破地震波所携带的能量随传播距离的增加,衰减趋势明显,且衰减速度快,其能量衰减以米计,有别于天然地震能量的衰减。爆破振动持续时间随爆心距的增加或能量的衰减并未呈现严格的变化趋势,表明振动持时不仅是能量与爆心距的函数,还受爆破地震波传播地段介质自身属性等因素影响。
由于受到矿区场地客观条件限制,振动监测点4(s4)被布置于平滑石壁上(未与地面刚性联结),导致振动监测存在较大失真可能性,故结合表2中数据对式(7)进行线性回归分析时,剔除信号s4相关数据,采用最小二乘法进行拟合,得到爆破振动持时的预测公式:
(8)
式中:α=1.002表明振动持时与信号能量相关性好,持时预测公式引入信号携带能量(Es)是合理的。公式线性拟合相关系数为89.7%,表明此式用于爆破振动持时预测切实可行,具有较高精度。
2 微差爆破延期时间优选
随着新型爆破器材的出现,通过高精度数码电子雷管可实现最小段间微差爆破延时毫秒差为1 ms,基于精确毫秒延时的控制爆破技术得到日益广泛的应用[5,13]。通过设置合理的段间延期时间可有效降低爆破振动强度、改善岩石爆破效果及扩大爆破规模。
2.1 爆破地震波线性叠加原理
单孔爆破获得的不同爆心距处振动信号中包含了爆区到测点间所有复杂地质条件下传播介质震动的属性。假设单段爆破地震波形是由无数个正弦谐波组成,谐波间相互干扰叠加,正、正相位间波形幅值叠加相长,致使地震波幅值增加,正、负相位间波形幅值叠加相消,致使地震波幅值降低。因此,微差爆破地震波形可以看作由一定数目的单段震波组成,即将爆破振动叠加过程假设为一个线性系统[5],可由下式表示:
(9)
式中:F(t)为由线性叠加法预测得到的微差爆破地震波形;m为一次爆破炸药总段数;fi(t)为单孔爆破地震波形。
由于基于实地记录得到的单孔爆破地震波形综合包含了传播介质地质条件和爆破条件的信息,而微差爆破其实是多个单孔爆破在不同时空下的组合,因此可以通过对实测单孔爆破地震波形进行线性叠加来表征微差爆破的地震波属性。
2.2 微差爆破延时优选应用实例
2.2.1 延时优选方法
基于地震波线性叠加原理,采用MATLAB 7.0编程,对图1中不同爆心距处各爆破振动波形进行线性叠加,优选微差爆破延期时间。假定叠加段数为5段,延期时间范围取为0~100 ms,典型微差延期时间与爆破振动峰值速度的关系曲线如图2所示,其中:Δt为爆破延期时间。
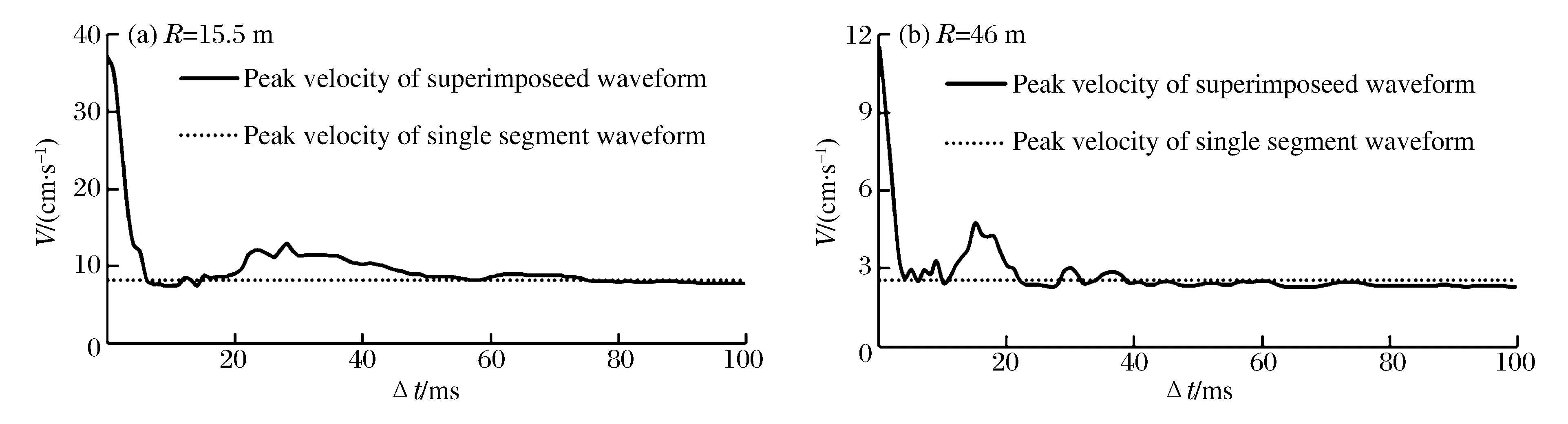
图2 延期时间与振动峰值速度的关系Fig.2 Variation of delayed time interval with peak velocity
由图2可以看出,选取合理的微差延期时间,可大幅降低爆破地震动强度,反之亦然。最大峰值速度对应的微差延期时间为0 ms,此时各段药包同时起爆,等同实际齐发爆破效果。当微差延期时间大于某一临界值时,线性叠加后的振动波形速度峰值趋于单段地震波峰值速度,此时可认为各分段地震波主振段已相互错开,尽管此时微差爆破地震动强度较低,但通常不利于岩体破碎,不能充分发挥微差爆破的优势。 为综合考虑爆破振动强度与岩石爆破效果两方面因素,定义延期时间在50 ms以内,且满足叠加峰值速度小于单段振波峰值速度的时间段作为采石场不同爆心距处合理微差延期时间值。通过统计得到不同爆心距处的合理微差延期时间,如表3所示,其中:ti和tI分别为合理延时区间和区间总长度。

表3 各测点的合理延时区间Table 3 Reasonable range of delayed time interval for each measuring point
由表3可以看出,合理微差延期时间往往不是某一具体的值,而是一个或多个时间区间,由此计算的合理延期时间更加便于爆破作业人员根据实地情况选择合适的爆破器材,从而实现微差爆破优势最大化。不同爆心距处,合理微差延期时间存在较大差异,表明合理微差延期时间的计算应考虑构筑物(被保护物)距爆源距离这一因素。爆心距为35.5 m处无符合前文定义的合理延时区间,主要是由于监测点基岩与地面非刚性联结,振动监测数据未准确反应爆破地震动固有属性,导致数据失真所致。
表3中,随爆心距的增加,各监测点合理延期时间有逐渐向大过渡的趋势,主要是由于随传播距离的增加,地震波中的纵波(P波)、横波(S波)以及面波(L波)因传播速度差异而逐渐分开。当超过某一临界距离后,地震波振动特性主要表现为波长大、振幅强、衰减慢的面波属性,因此基于线性叠加原理的微差爆破延期时间优选值有逐渐增加的趋势。
表3中不同爆心距处合理延时区间总长度长短参差不齐,无明显规律可循,反映出爆破地震波的振动随机性与复杂性。
2.2.2 工程应用

图3 采石场图片Fig.3 Picture of the quarry
堰口采石场矿区沟谷发育,地表切割强烈,地层及岩性简单,矿体主要成分为晋宁期辉绿岩(βμ),岩石裂隙不发育,大部分呈闭合状态。采石场地貌如图3(a)所示。
在距离爆区约300 m处的砖混结构民房处布置监测点,重复至少3次单孔爆破试验,尽量保证每次试验时装药结构与装药量(TNT当量为35.6 kg)一致,待单孔爆炸振动波形监测结果稳定,采用前文所述延时优选方法(叠加段数为12段),计算得到民房处合理延时区间为20~25 ms。结合采石场岩性实际,综合考虑爆破地震动强度、岩石破碎效果及爆破网络可靠性等因素,最终选用高精度数码电子雷管替代传统导爆管雷管实现孔间延时,控制单次爆破规模不大于500 kg,孔径d=90 mm,孔距a=3 m,排距b=2.5 m,孔深h=10 m,延时Δt=20 ms,堵塞不小于3.5 m。变更爆破参数后,民房处爆破振动速度峰值最大为0.332 mm/s,小于单孔炸药爆破时峰值速度(0.339 mm/s),且岩石爆破效果得到显著改善,如图3(b)所示。
3 结 论
(1) 爆破振动信号能量是速度、频率、持续时间的综合表征,与振动持续时间相关性好,振动持时预测公式引入信号携带能量(Es),可提高预测精度。(2) 爆破振动持续时间与比例速度负相关,与比例药量正相关。(3) 合理微差延期时间往往不是某一具体值,而是一个或多个时间区间;不同爆心距处合理微差延期时间值不同。
[1] 魏晓林,郑炳旭.干扰减振控制分析与应用实例[J].工程爆破,2009,15(2):1-6,69. Wei Xiaolin, Zheng Bingxu. Analysis of control blasting-induced vibration and practice[J]. Engineering Blasting, 2009,15(2):1-6,69.
[2] 张光雄,杨军,卢红卫.毫秒延时爆破干扰降振作用研究[J].工程爆破,2009,15(3):17-21. Zhang Guangxiong, Yang Jun, Lu Hongwei. Research on seismic wave interference effect of millisecond blasting[J]. Engineering Blasting,2009,15(3):17-21.
[3] 傅洪贤,沈周,赵勇,等.隧道电子雷管爆破降振技术试验研究[J].岩石力学与工程学报,2012,31(3):597-603. Fu Hongxian, Shen Zhou, Zhao Yong, et al. Experimental study of decreasing vibration technology of tunnel blasting with digital detonator[J]. Chinese Journal of rock mechanics and Engineering, 2012,31(3):597-603.
[4] 高富强,侯爱军,杨小林,等.基于量纲理论的爆破振动持续时间分析[J].金属矿山,2010(9):143-145. Gao Fuqiang, Hou Aijun, Yang Xiaolin, et al. Analysis of blasting vibration duration based on dimension theory[J]. Metal Mine, 2010(9):143-145.
[5] 杨年华,张乐.爆破振动波叠加数值预测方法[J].爆炸与冲击,2012,32(1):84-90. Yang Nianhua, Zhang Le. Blasting vibration waveform prediction method based on superposition principle[J]. Explosion and shock waves, 2012,32(1):84-90.
[6] 李洪涛,卢文波,舒大强,等.爆破地震波的能量衰减规律研究[J].岩石力学与工程学报,2010,29(S1):3364-3369. Li Hongtao, Lu Wenbo, Shu Daqiang, et al. Study of energy attenuation law of blast-induced seismic wave[J]. Chinese Journal of rock mechanics and Engineering, 2010,29(S1):3364-3369.
[7] 赵明生,梁开水,李本伟.段药量对爆破振动信号时频特性的影响研究[J].振动与冲击,2012,31(7):85-88. Zhao Mingsheng, Liang Kaishui, Li Benwei. Influence of deck charge on time-frequency characteristics of a blasting vibration signal[J]. Journal of Vibration and Shock, 2012,31(7):85-88.
[8] 阳生权,廖先葵,刘宝琛.爆破地震安全判据的缺陷与改进[J].爆炸与冲击,2001,21(3):223-228. Yang Shengquan, Liao Xiankui, Liu Baochen.Default of the judging standard of blasting vibration safety abstract[J]. Explosion and shock, 2001,21(3):223-228.
[9] 凌同华,李夕兵.单段爆破振动信号频带能量分布特征的小波包分析[J].振动与冲击,2007,26(5):41-43. Ling Tonghua, Li Xibing. Features of energy distribution of single deck blast vibration signals with wavelet packet analysis[J]. Journal of Vibration and Shock, 2007,26(5):41-43.
[10] 刘敦文,粟闯,龚运高.一种基于爆破振动信号小波分析的爆破危害评判新方法[J].中南大学学报,2010,41(4):1574-1577. Liu Dunwen, Su Chuang, Gong Yungao. New method for blasting hazards evaluation based on wavelet analysis of blasting vibration signals[J]. Journal of Central South University, 2010,41(4):1574-1577.
[11] 徐国元,中国生,熊正明.基于小波变换的爆破地震安全能量分析法的应用研究[J].岩土工程学报,2006,28(1):24-27. Xu Guoyuan, Zhong Guosheng, Xiong Zhengming. Study and application of energy analysis method for blasting seismic safety based on wavelet transform[J]. Journal of geotechnical engineering, 2006,28(1):24-27.
[12] 中国生,徐国元,熊正明.基于小波变换的爆破地震信号能量分析法的应用研究[J].爆炸与冲击,2006,26(3):222-227. Zhong Guosheng, Xu Guoyuan, Xiong Zhengming. Application research of the energy analysis method for blasting seismic signals based on wavelet transform [J]. Explosion and shock, 2006,26(3):222-227.
[13] 何理,钟冬望,刘建程,等.微差爆破试验及爆破振动能量的小波包分析[J].金属矿山,2014(6):10-15. He Li, Zhong Dongwang, Liu Jiancheng, et al. Millisecond blasting tests and wavelet packet analysis of blasting vibration energy[J]. Metal Mine, 2014(6):10-15.
[14] 李的林,高振儒,朱立新.爆破震动危害中几个重要因素分析[J].工程爆破,1999,5(3):64-67. Li Delin, Gao Zhenru, Zhu Lixin. Analysis on several principal factors of blasting vibration hazards[J]. Engineering Blasting,1999,5(3):64-67.
[15] 尹力峰,祝慧勤,石钦.喀拉朔克水库坝区场地的设计地震波[J].内陆地震,2005,19(3):233-240. Yin Lifeng, Zhu Huiqin, Shi Qin. Designing seismic vaves at the site of kalashuoke reservir[J]. Inland Earthquake, 2005,19(3):233-240.
[16] 马行瑞,陶良.弹性波反演方法及应用[M].北京:科学出版社,1999.
[17] 王国华,段希祥,杨溢,等.一起硝酸铵爆炸事故的破坏效应[J].爆破,2009,26(3):104-107. Wang Guohua, Duan Xixiang, Yang Yi, et al. Destructive effect of explosion incident of ammonium nitrate[J]. Blasting, 2009,26(3):104-107.
(责任编辑 王小飞)
Analysis of blasting vibration duration and optimizing of delayed time interval for millisecond blasting
Zhong Dongwang1,2, He Li1,2, Cao Peng2, Zhang Kui3
(1.CollegeofScience,WuhanUniversityofScienceandTechnology,Wuhan430065,Hubei,China;2.CRPCE-WUSTBlastingTechnologyResearchCenter,Wuhan430065,Hubei,China;3.HubeiHaoshengBlastingEngineeringCo.,LTD,Shiyan442012,Hubei,China)
Duration of blasting vibration and delayed time interval of millisecond blasting are respectively an important indicator for assessing and controlling blasting hazards. It is therefore of great necessity to explore the factors that may influence the duration and the ways that can optimize the interval. In the present work, combined with dimensional analysis, we examined the factors influencing the duration arrived at a formula for predicting the blasting vibration duration, whose linear correlation reached 89.7%. Based on the linear superposition theory of seismic wave, the reasonable range of delayed time interval with different distances between the blasting source and the measuring point was obtained using MATLAB7.0. The result shows that there is close correlation between the signal energy and the duration of blasting vibration, the accuracy of prediction can be improved by introducing the signal energy into the predictive formula, the duration is negatively related to the proportional velocity and positively related to the proportional charge weight, and the reasonable range of the delayed time interval between the blasting holes is not always a specific value but may be one or more time intervals, which are determined by different distances between the explosion source and the measuring point. The application of the formula in actual engineering shows that our predictive formula and optimization for millisecond blasting are highly practicable.
mechanics of explosion; duration of blasting vibration; dimensional analysis; delayed time interval; linear superposition tTheory; millisecond blasting
10.11883/1001-1455(2016)05-0703-07
2013-04-12;
2013-07-28
国家自然科学基金项目(51574184);湖北省教育厅科学技术研究项目(Q20161101); 武汉科技大学青年科技骨干培育计划项目(2016xz018)
钟冬望(1963- ),男,教授,博士生导师;
何 理,emp-heli@hotmail.com。
O381国标学科代码:13035
A
