“大问题”教学谈——以“的士收费”为例
2016-04-15谭利萍
谭利萍 叶 俊
“大问题”教学谈——以“的士收费”为例
谭利萍叶俊

前不久,学校进行15分钟片段教学比赛。我想:15分钟,能够给学生传递什么呢?如果给学生抛出一个“大问题”,让他们进行自主学习,教师做适时的引导,收效会不会远胜于我传授给他们的知识呢?
这里所说的“大问题”,是指具有思维的深度,具有探究学习的挑战性,蕴含丰富的活动体验,有利于学生的小组合作学习和探究学习的数学问题。学生要求具有“能根据解决问题的需要,收集有关信息,进行归纳、整理、类比与猜想,发展初步的合情推理能力”。合情推理虽不是一个严密的推理形式,却是数学探究和发现中必不可少的一种思维能力。
1.出示情境图,收集信息

师:当当和哥哥一起乘坐出租车放学回家。到站了,要付费了。请看图。从图中你能获得哪些数学信息呢?请将你收集到的信息列在学习卡上。对于收集到的数学信息,你有不明白的地方吗?同学之间能不能互相解答?
生1:3km以内7元是不是1km也是7元,2km也是7元。
生2:是的。只要在3km以内都是7元。
师:那2.9km呢?
生2:还是7元。
师:哦,那7元就是我们常说的起步价了。
生3:不满1km按1km收费是什么意思?
生4:只要超过3km,比如3.1km就要看作4km收费了。也就是超过3km一直到4km都按4km收费,超过4km直到5km都按5km收费。
师:这也就是我们常说的“进一法”计数。那今天图上的6.3km就要按几km计费呢?
生4:7km。
【设计意图】通过一张学习卡,帮助学生在情境图中找到有用的数学信息,并进行整理。遇到不懂的数学信息,师生在互动中理解清楚。
2.提出问题,解决问题
师:司机阿姨说要付费13元,你认为对吗?你会怎样判断收费呢?请独立思考,并将你解决的过程写在学习卡上。
学生先思考解决问题的过程,然后书写。
师:请大家说说你是怎样解决的。
生5:我是根据分段里程验证总价。7+1.5×(7-3)=7+6=13(元),所以司机阿姨说要付13元是对的。
生6:我是根据总价验证里程。13-7=6(元),6÷ 1.5=4(km),3+4=7(km),6.3km→7km,当当他们行驶了6.3km,按7km收费,是对的。
生7:我是先全程按单价计费,再找差。1.5×7=10.5(元),前3km少算7-1.5×3=2.5(元)。
师:请观察以上同学的解答,你发现他们的解题思路有什么相同和不同的地方?
生8:第1、3种方法都是通过知道路程再计算总价的方法验证13元对不对。
生9:第2种方法是已知总价钱,倒过来推导走的路程是不是对的。
师:也就是说,题目的条件虽然很多,但是我们可以通过合适的条件得到一个结论,再与题中给出的信息做比较,看是否合理。也就是说我们既可以用乘法解决这个问题,也可以用除法解决,对吧。大家真动脑!
【设计意图】这道题在教材中是直接给出路程和单价,要学生解决分段收费求总价的问题。在课后练习题中,又出现了一个给出总价要学生倒过来求路程的拓展提高题。在这里,我们把这两个问题都作为已知条件抛给学生,形成一个大问题。这样一来,题目的思维难度大大提高。但难度的提高,给了不同学生学习不同数学的平台。在这个过程中,学生的创造性思维得到了发展,有的孩子能在短短的时间内用不同的方法解决此类问题。
3.结合具体问题,初步渗透函数思想
师:刚刚我们计算的是的士收费问题,我们知道在生活中很多时候都有这种分段计费的问题。我们把刚刚的的士分段计费做成一个统计表,可以吗?
生:当然可以的。我们现在就可以填写。
学生动手设计统计表并填表。
师:老师将你们的分段计费统计表做成了一个统计图,想看吗?(PPT展示分段计费统计图)这与我们之前学过的统计图有什么不同呢?
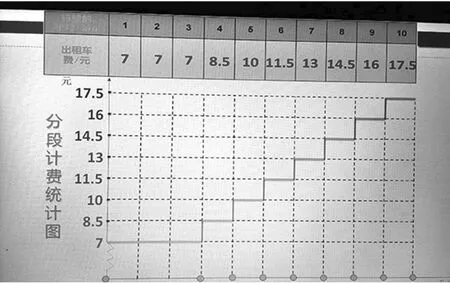
生10:每一段距离,它的收费都是不一样的。
师:从统计表和统计图中,你能发现什么规律?
生11:3km以内全是7元。
生12:3km以外,每增加1km都增加了1.5元。
4.拓展延伸
师:我们已经学过用字母表示数了,如果用字母a表示行驶的路程(千米),用字母C表示收费总价(元),你可以表示出总价C与路程a之间的关系吗?
生:这个有点难,可以试试。
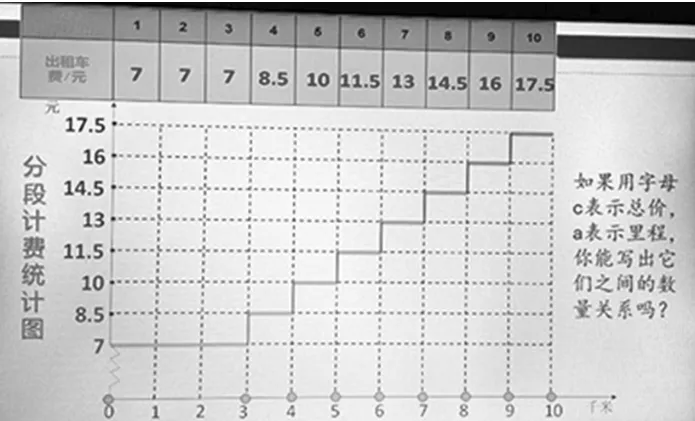
师:注意了,这里的路程a是有要求的,必须是大于3,才可以这样表示。如果a在0到3之间,总价C=7元了。
由于这次片段教学比赛是在学生学习完“用字母表示数”单元的知识基础上进行的,因此在上这个片段时,我们想到能不能尝试进行拓展,也就是引导学生用含有字母的关系式表达总价和路程之间的关系。15分钟的片段确实时间不够,但是如果是上一节课,这个拓展是可以展示给学生的。大问题的提出还是需要立足于一定的认知基础。
大问题的提出与解决过程,就是一个知其然还要知其所以然的过程,也是一个不断丰富自己解决问题的方法的过程。围绕大问题,学生经历了收集信息,选择合适信息解决问题的过程,也感悟了数学研究的思想,学习了探索知识的方法,掌握了自主学习的技巧,培养了创造性的思维能力。
(作者单位:长沙市麓山国际实验学校)
