基于一致系数求积的广义牛顿法求解非线性方程组

姚腾腾(厦门大学数学科学学院,福建厦门361005)



基于一致系数求积的广义牛顿法求解非线性方程组

姚腾腾
(厦门大学数学科学学院,福建厦门361005)

摘要:采用一致系数求积公式近似逼近泰勒余项,得到一种新的求解非线性方程组的广义牛顿法.给出算法的一般形式,证明算法是三阶收敛的,并且在一定的温和条件下可以达到五阶收敛.最后,给出数值例子说明算法的有效性和稳定性.

关键词:一致系数求积;广义牛顿法;非线性方程组;三阶收敛

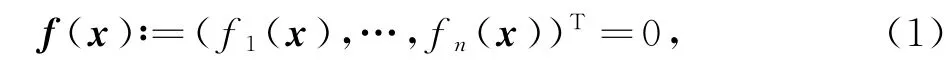
其中x=(x1,x2,…,xn)T∈Rn,f:K⊆Rn→Rn在凸集K中是充分Fréchet可微的.众所周知,牛顿法是求解非线性方程组(1)的经典迭代法.而近几年,出现了许多利用Adomian分解、同伦摄动、牛顿柯特斯求积等技巧求解非线性方程组(1)的牛顿衍生算法[1-8],这些方法相较于牛顿法具有更高的收敛性.在本文中,我们提出一种新的广义牛顿迭代算法,即采用基于一致系数求积的牛顿法求解非线性方程组(1).此广义牛顿迭代法只需要估计f(x)以及它在不同点处的雅可比矩阵即可.数值实验表明,这个迭代算法是三次收敛的并且在一定的温和条件下可达到五阶收敛.

1　预备知识

一致系数求积公式[9]定义如下形式的积分

这里ρ(x)是权函数,通常式(2)的不定积分无法求解,为此我们需要定义能够近似I(f)的数值积分公式.典型的数值积分公式具有如下形式:

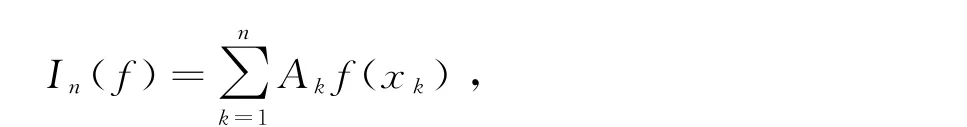
其中xk称为求积公式的节点,Ak称为求积系数.假设ρ(x)=1,则n个节点的一致系数求积公式具有如下简单形式

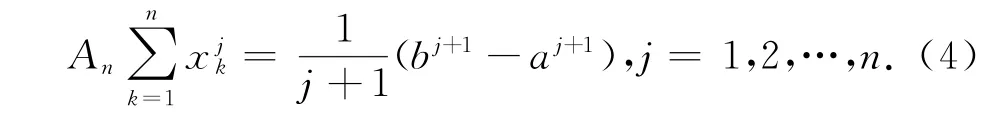
由文献[10]知,节点xk是关于积分区间的中点对称的.

对任意的x,xs∈K,由泰勒定理[10]得

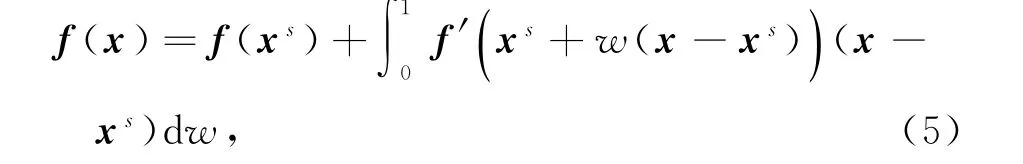
其中f'(x)为函数f在点x∈Rn处的雅克比矩阵.通过积分变换有

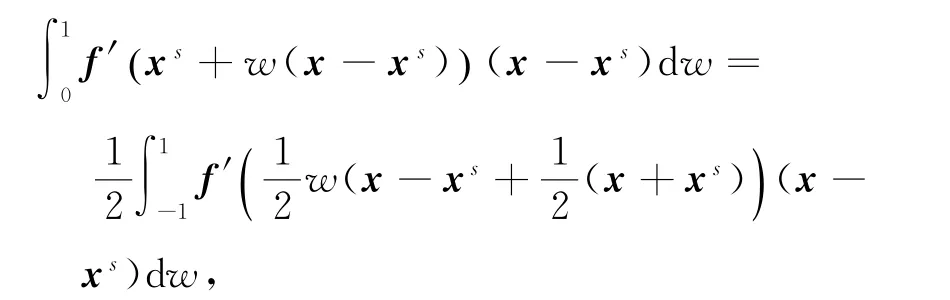
应用M个节点的一致系数求积公式,得到如下的数值积分逼近:

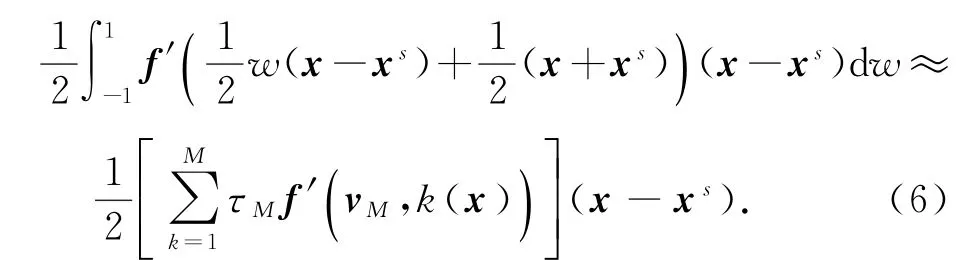
其中

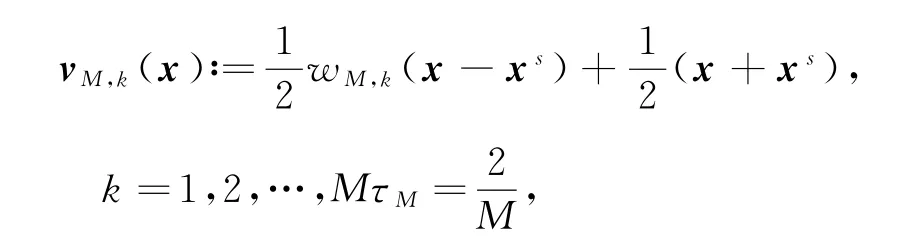
节点wM,k表示M个节点中的第k个节点,则由节点关于原点对称,满足

注1 我们知道M个节点的一致系数公式具有至少M次代数精度,并且M为偶数时,代数精度为M+1.因此,当M≥2时,有

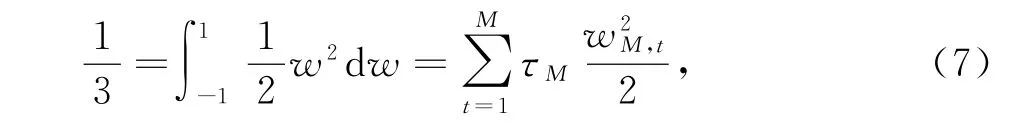
以及

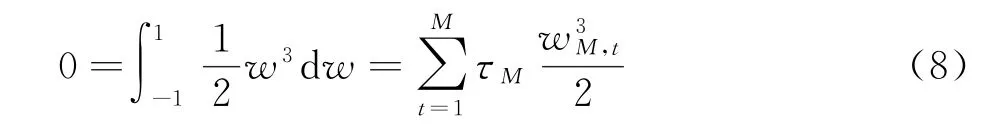
成立.

注2 如果能建立求积公式(3),那么必须要求式(4)中的节点xk,k=1,2,…,n为不同的实数,而当n =8以及n≥10时,解得式(4)中总会出现一对复共轭节点.因此,在这些情形下无法构造一致系数公式.

2　算法及其收敛性分析

基于以上讨论,我们给出一种新的基于一致系数求积公式求解非线性方程组(1)的广义牛顿迭代算法.

算法1 (基于一致系数求积公式的广义牛顿法)

Step 0 给定初值x0∈Rn以及正整数M.s∶=0.

Step 1 计算ys=xs-f'(xs)-1f(xs).

Step 2 计算

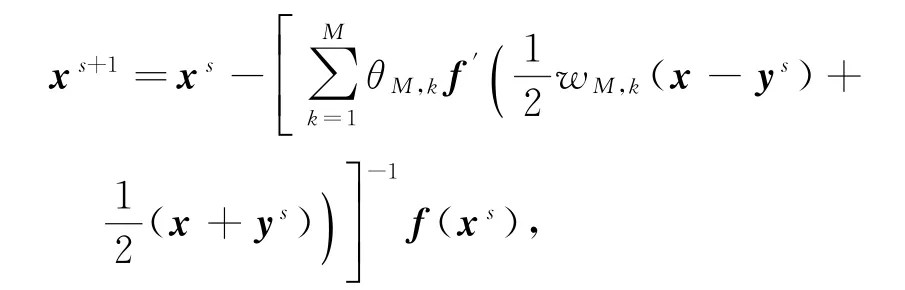
Step 3 s∶=s+1返回到Step 1.

由于节点{wM,k}是关于原点对称的,并且当M为奇数时,原点必是节点,加上系数θM,k的取法,可得如下关系式

下面证明,上述建立的求解非线性方程组(1)的算法1是局部三次收敛的.假设α∈Rn是非线性方程组(1)的一个解,f在α的一个邻域N(α)内是充分连续可微的.对任意的x∈N(α),J(x)∈Rn×n为f在点x处的雅克比矩阵,即

这里假设J(x)对任意x∈N(α)都是非奇异的,并且定义H(x)为J(x)的逆矩阵.那么得到

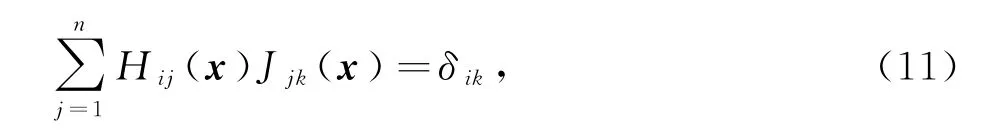
其中δik是克罗内克符号函数.对等式(11)两边相对于xl求微分,可以得到

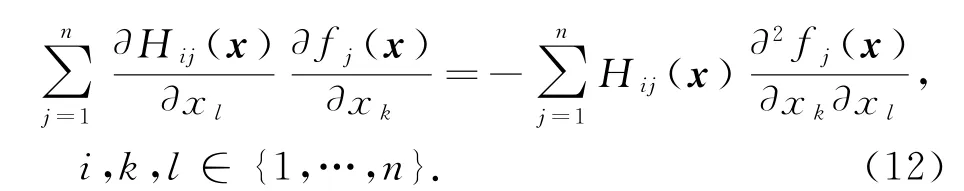
下面我们给出所需的两个引理,类似于文献[3]的证明过程,引理可以很容易地得到.

引理1 对任意x∈N(α),定义y(x)=(y1(x), …,yn(x))∈Rn为经典牛顿法的迭代函数:

有

和

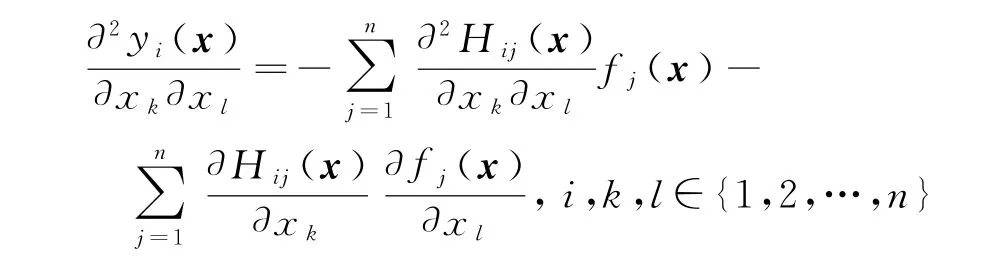
成立.特殊的有

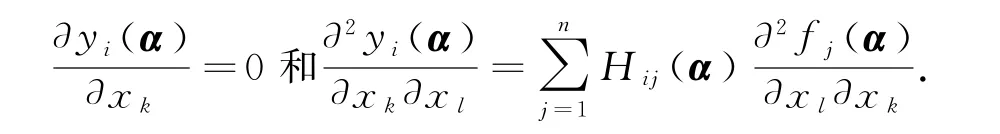
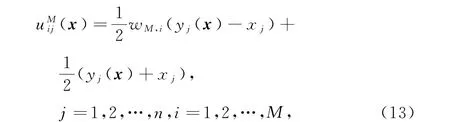
其中uMi(x)=(uMi1(x),uMi2(x),…,uMin(x))T∈Rn.那么有等式

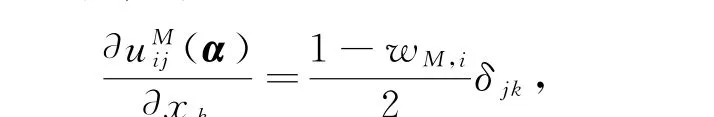
和

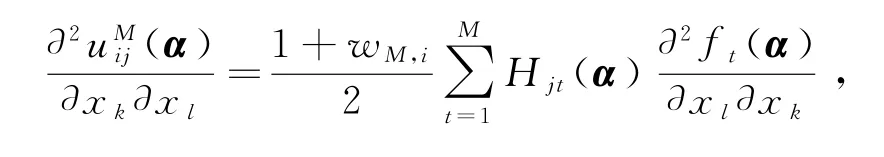
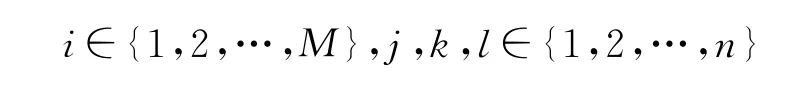
成立.

接下来,我们给出算法1的局部三次收敛性定理.

定理1 函数f:N(α)⊆Rn→Rn在α∈Rn的一个邻域N(α)内是充分可微的,α是非线性方程组(1)的一个解.选取充分接近解α的初始值x0并且假设J(x)在邻域N(α)内是连续非奇异的.那么算法1产生的序列{xk}是三次收敛到α的.

证明 任意给定x∈N(α),我们定义W(x)= Z-1(x),这里

对每一个x∈Rn,定义g(x)∶=(g1(x),…,gn(x))T,其中

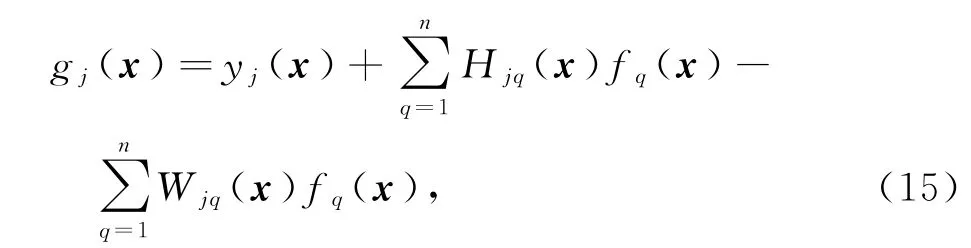
对每一个j∈{1,…,n},gj(x)在点α处泰勒展开

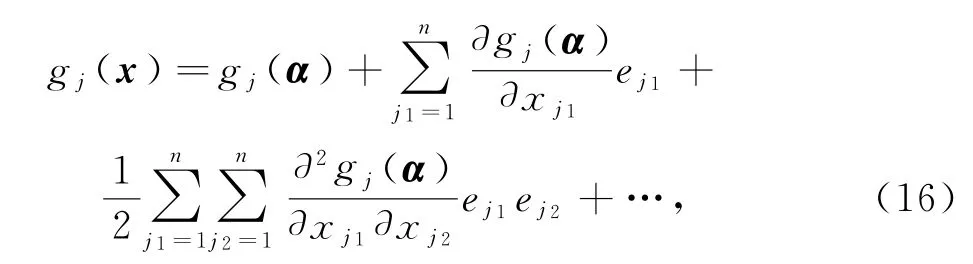
其中ejk=xjk-αjk.

首先,我们证明∂gj(α)/∂xk=0,j,k∈{1,2,…, n}.式(15)两边同时左乘Zij(x),

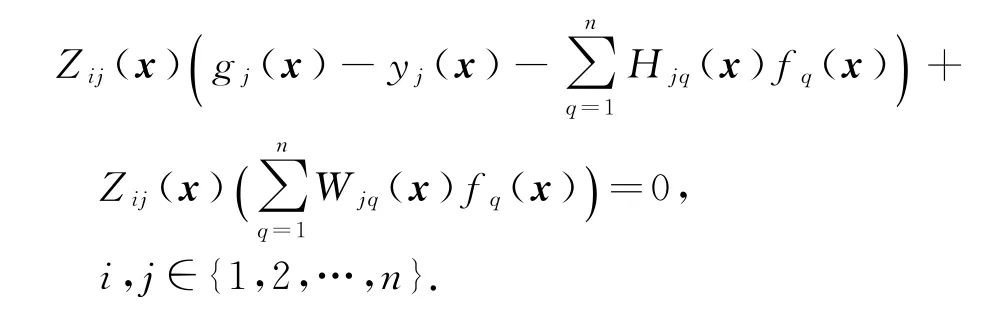
那么

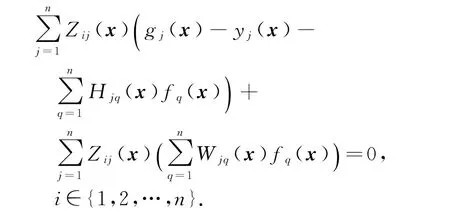
应用W(x)=Z-1(x),等式简化为

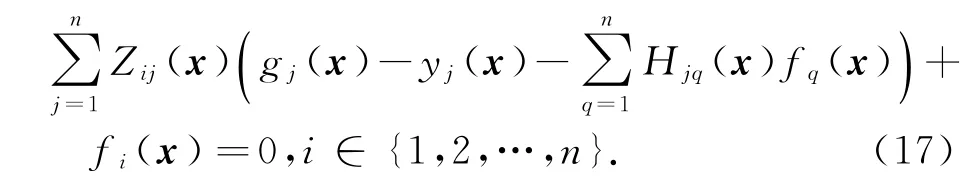
对式(17)两边相对于xk求微分,应用式(11)和引理1可得

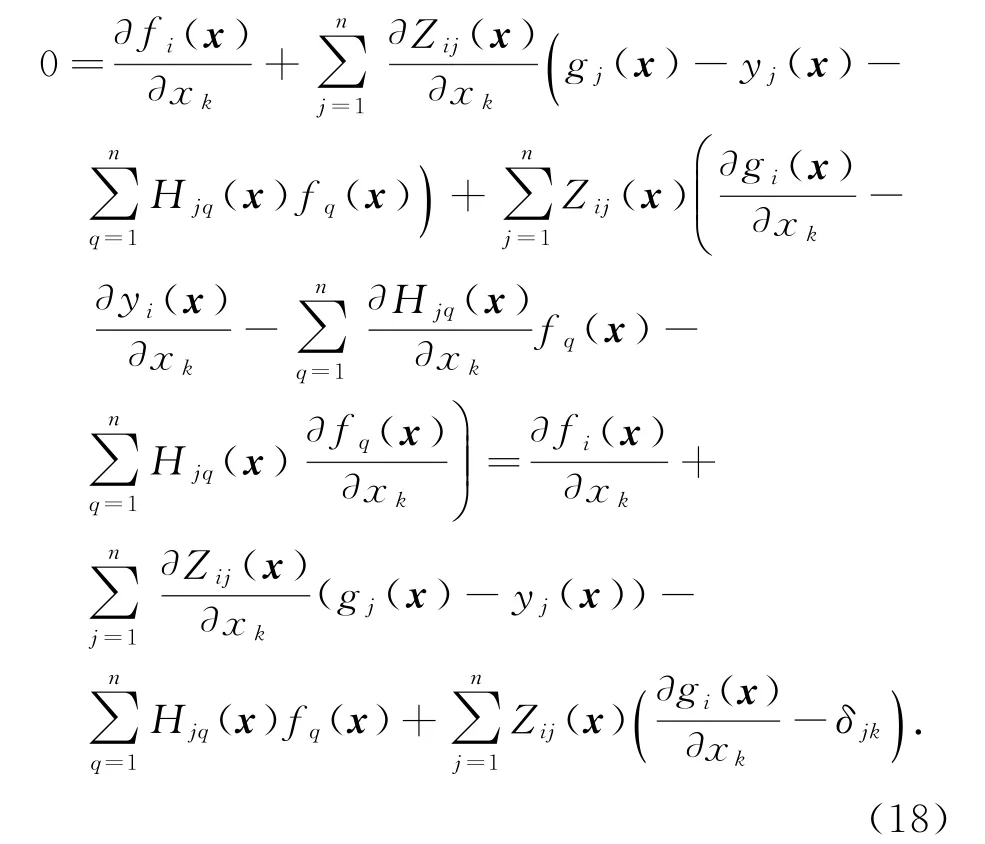
上式中令x=α,应用式(10)得

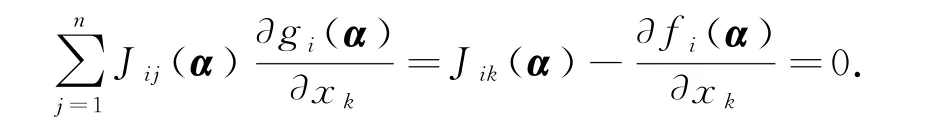
由假设J(x)对所有x∈N(α)都是非奇异的,所以有

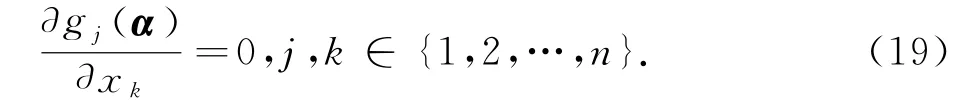
接下来,我们证明∂2gj(α)/(∂xk∂xl)=0,j,k,l ∈{1,2,…,n}.对式(18)两边相对于xl取微分,应用式(11)和引理1,得到

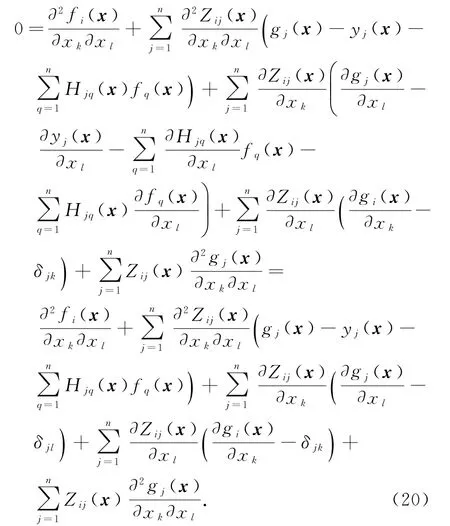
令x=α并将式(19)代入到式(20)得,

另一方面,根据式(14),有

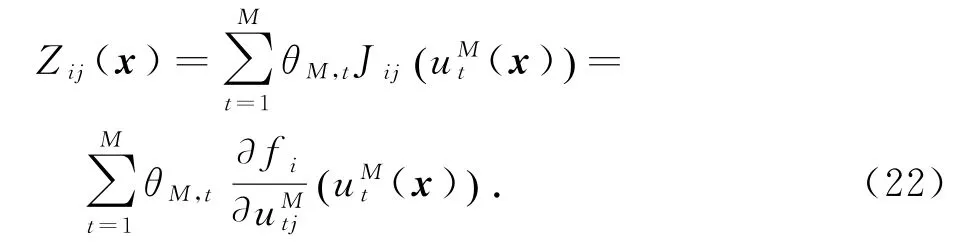
对方程(22)两边相对于xk取微分得到,

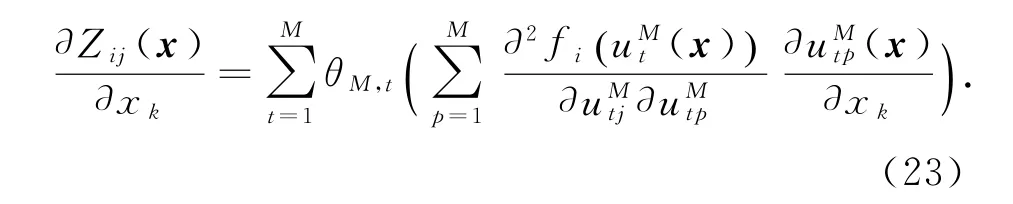
令x=α并应用引理2,式(23)为

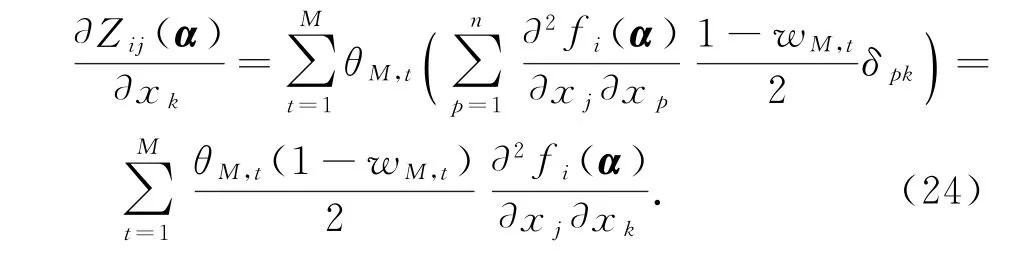
由于函数fi(x)是充分可微的,将式(24)代入到式(21)满足

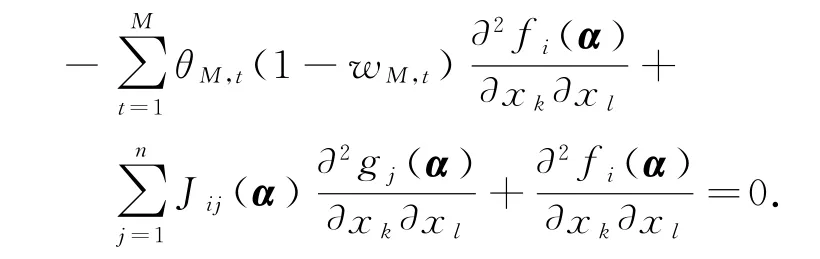
结合式(9),有

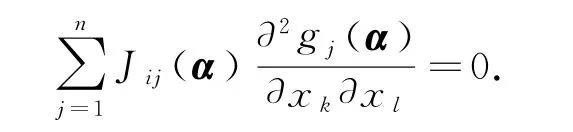
由假设J(α)是非奇异的,所以有

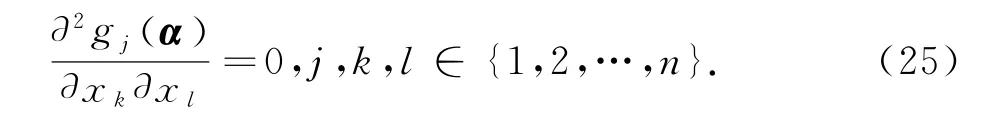
因此,由式(16),(19)和(25)可知算法1是三次收敛的.

定理2 如果定理1中的假设成立,M≥2并且f的坐标函数{fi}满足∂2fi(α)/(∂xj∂xk)=0,i,j,k ∈{1,2,…,n},那么算法1产生的序列{xk}是五阶收敛到α的.

证明 我们首先证明∂3gj(α)/(∂xk∂xl∂xm)= 0,j,k,l,m∈{1,2,…,n}.对式(23)两边相对于xl取微分,并令x=α,应用引理2计算可得

另一方面,对式(20)两边相对于xm取微分,然后令x=α由式(11),(19)和(25)和引理1得到

将式(26)代入到式(27)有

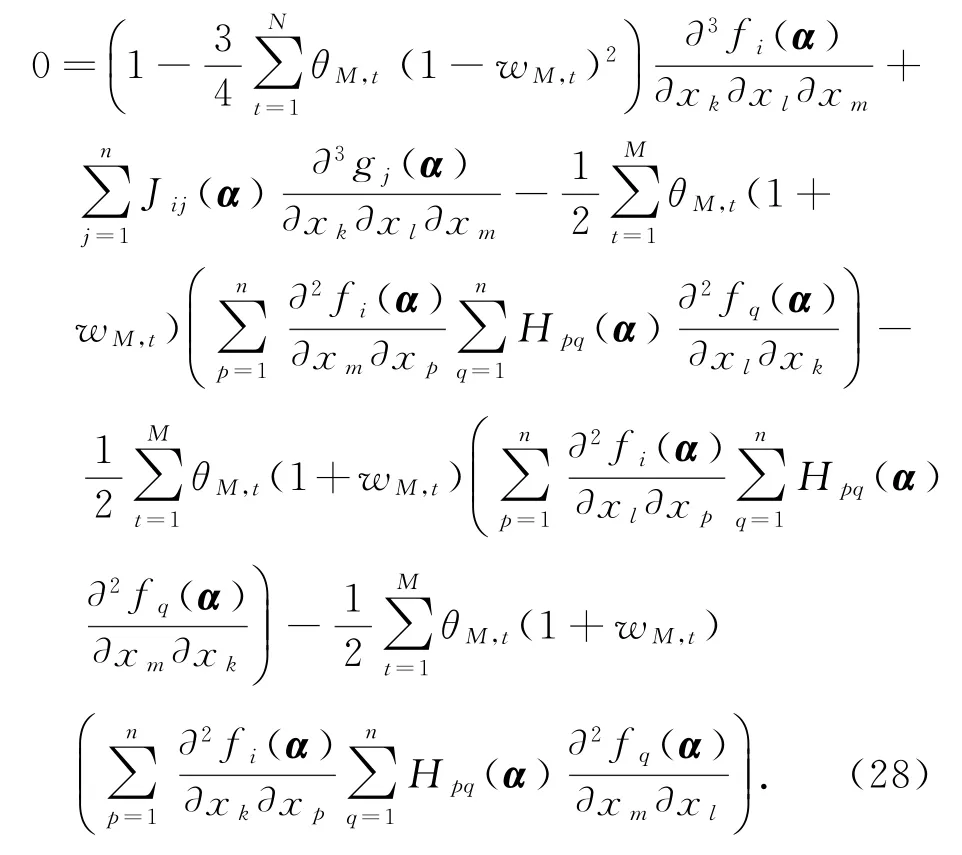
由假设M≥2,∂2fi(α)/(∂xj∂xk)=0,i,j,k∈{1,2,…,n},通过式(7),(9)和(28)有

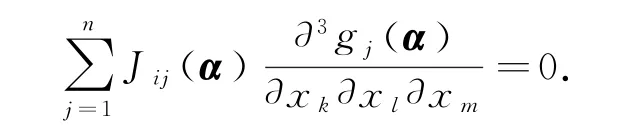
由J(α)的非奇异性,可得

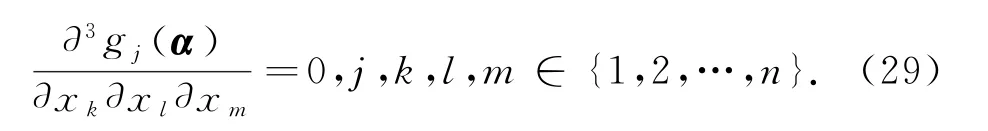
类似的,我们证明∂4gj(α)/(∂xk∂xl∂xm∂xr)= 0,j,k,l,m,r∈{1,2,…,n}.对式(23)两边求二次微分,然后令x=α应用式(7),(8),引理2和假设∂2fi(α)/(∂xj∂xk)=0,i,j,k∈{1,2,…,n},有

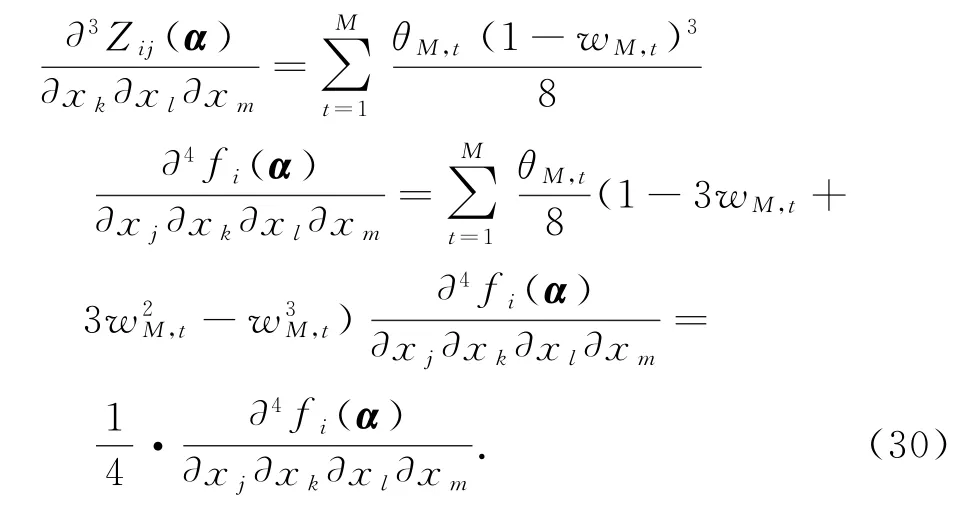
另一方面,对式(20)两边求二次微分,并令x=α应用式(19),(25),(29)和引理1有

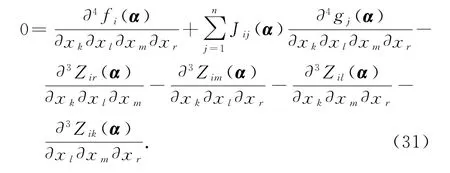
我们将式(30)代入到式(31)中,可得

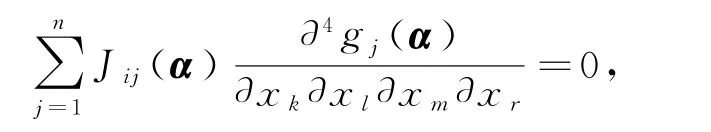
由J(α)的非奇异性,有

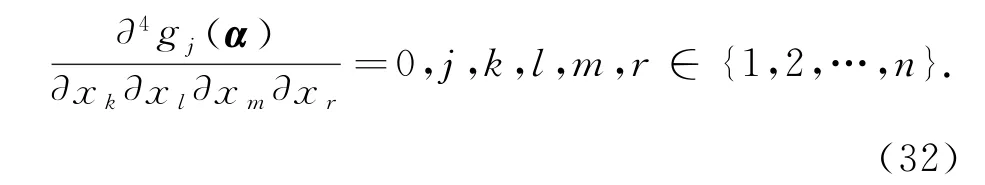
由式(16),(19),(25),(29)和(32)可得算法1是五阶收敛的.

3 数值实验

下面例子1～3中,实验停止的标准设为

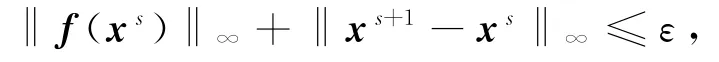
其中‖·‖∞指无穷范数.如文献[3]中一样,方法的收敛阶p由如下的近似值给出

例子1[3]考虑如下非线性方程组:

非线性方程组的解为α=(0.577 350,0.577 350, 0.577 350,-0.288 675)T.这里我们给出初始值为x0=(0.6,0.6,0.6,-0.2)T.

例子2[11]考虑如下非线性方程组:

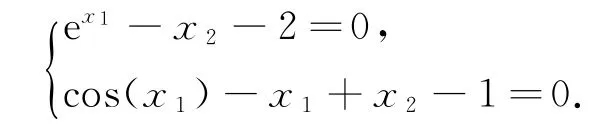
非线性方程组的解为α=(1.478 489;2.386 312)T.这里我们给出初始值为x0=(1.2,2.0)T.

例子3[3]考虑如下非线性方程组:

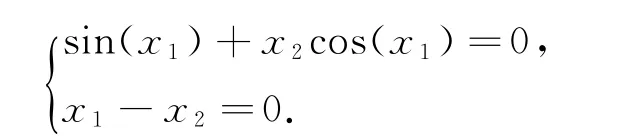
非线性方程组的解为α=(0,0)T.这里我们给出初始值为x0=(0.4,0.4)T.

例子4[11]考虑如下非线性方程组:

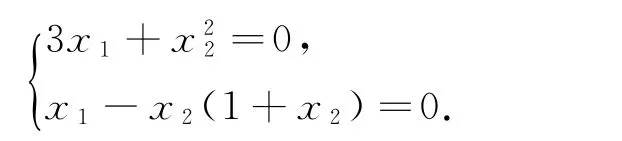
非线性方程组的解为α=(0,0)T.这里我们给出初始值为x0=(0.5,1)T.

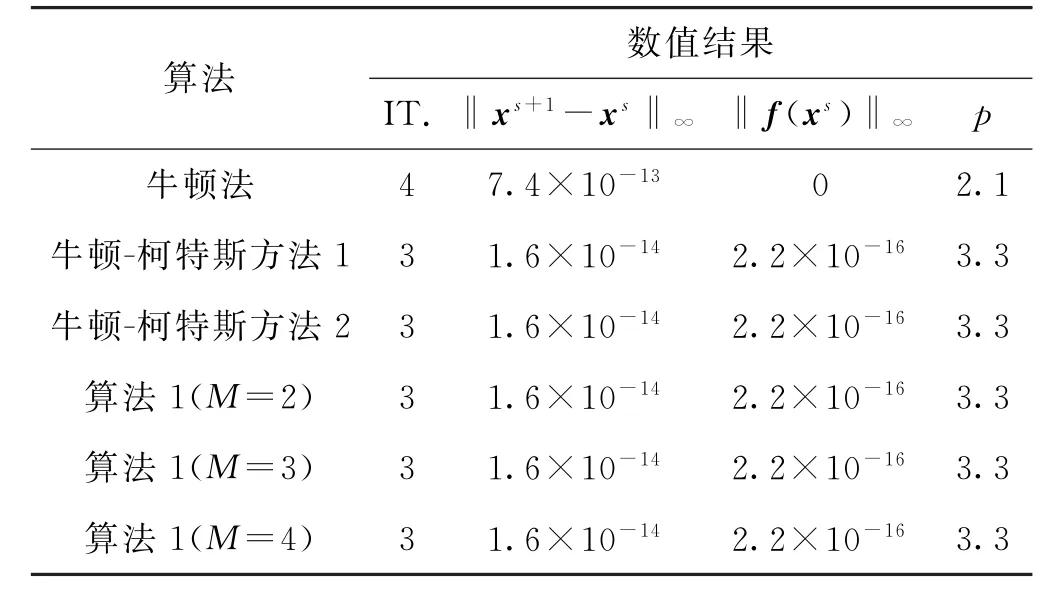
表1　例子1的数值结果(ε=10-11)Tab.1 Numerical result of example 1(ε=10-11)

表2　例子2的数值结果(ε=10-11)Tab.2 Numerical result of example 2(ε=10-11)

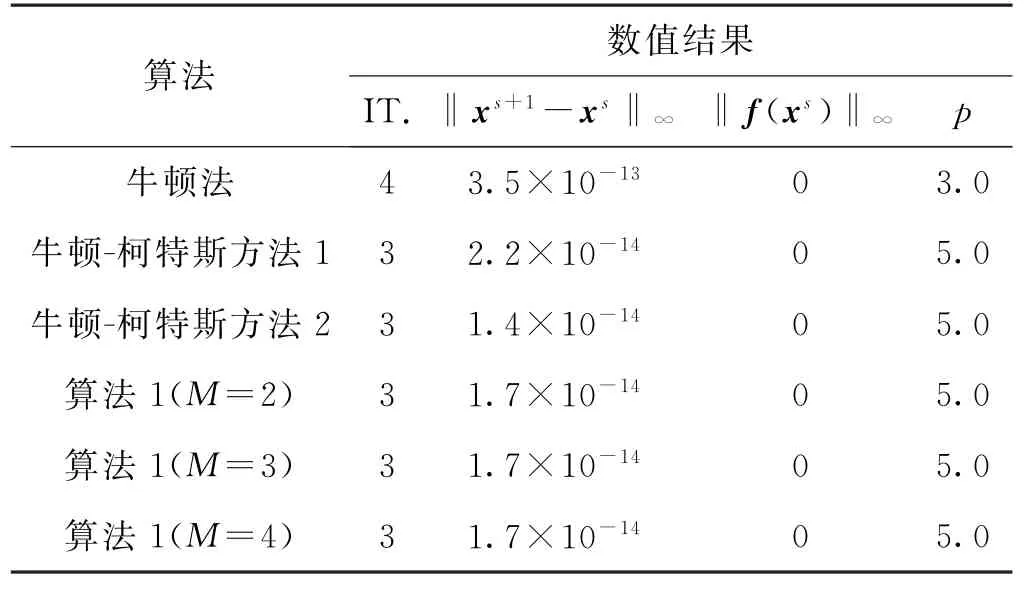
表3　例子3的数值结果(ε=10-11)Tab.3 Numerical result of example 3(ε=10-11)

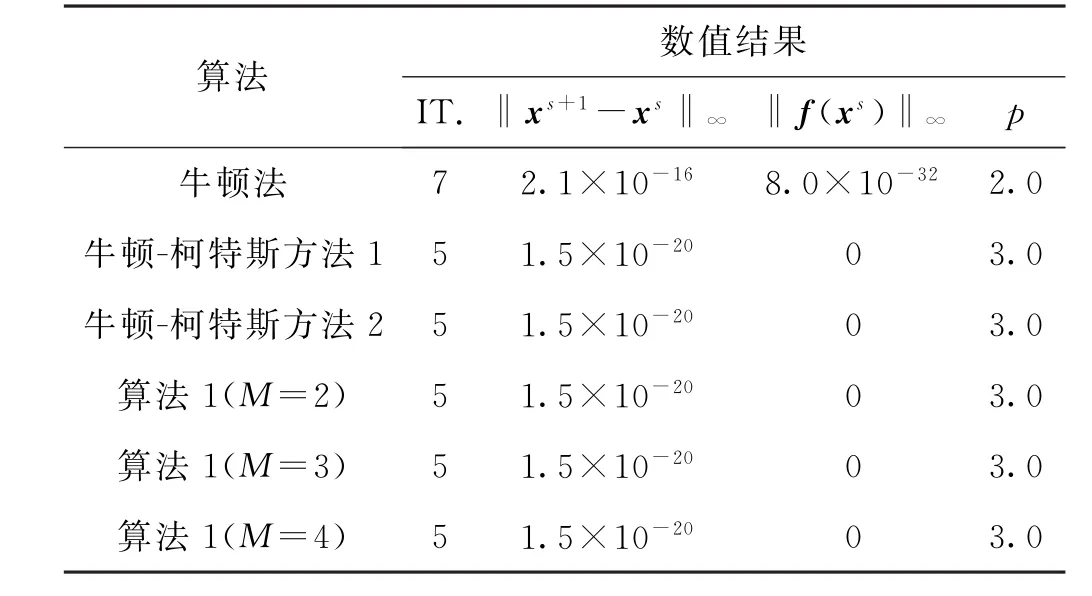
表4　例子4的数值结果(ε=10-11)Tab.4 Numerical result of example 4(ε=10-11)

表1～4中IT.,‖xs+1-xs‖∞,和‖f(xs)‖∞分别表示算法迭代步数、算法最后两步迭代点之间的距离,以及算法最后迭代值的残差.表格1～4表示新算法1与牛顿法和牛顿-柯特斯方法作比较.例子3满足温和条件∂2fi(α)/(∂xj∂xk)=0,i,j,k∈{1,2},定理2保证了算法的五阶收敛性.从表格中我们可以看出新算法1仍然能保持很好的收敛性质,并且相对牛顿-柯特斯方法系数要求更自由.

参考文献:

[1] BABAJEE D K R,DAUHOO M Z,DARVISHI M T.et al.A note on the local convergence of iterative methods based on Adomian decomposition method and 3-node quadrature rule[J].Appl Math Comput,2008,200: 452-458.

[2] CORDERO A,TORREGROSA J R.Variants of Newton' s method for functions of several variables[J].Appl Math Comput,2006,183:199-208.

[3] CORDERO A,TORREGROSA J R.Variants of Newton' s method using fifth-order quadrature formulas[J].Appl Math Comput,2007,190:686-698.

[4] DARVISHI M T,BARATI A.A third-order Newton-type method to solve systems of nonlinear equations[J].Appl Math Comput,2007,187:630-635.

[5] GOLBABAI A,JAVIDI M.A new family of iterative methods for solving system of nonlinear algebric equations[J].Appl Math Comput,2007,190:1717-1722.

[6] NOOR M A.Some applications of Newton-Cotes formula for solving nonlinear equations[J].Int J Appl Math Eng Sci,2010,4:43-52.

[7] NOOR M A,WASEEM M.Variant of Newton method using fifth-order quadrature formula:revisited[J].J Appl Math&Inform,2009,27:1195-1209.

[8] SÁNCHEZ M G,PERIS J M,GUTIÉRREZ J M.Accelerated iterative methods for finding solutions of a system of nonlinear equations[J].Appl Math Comput,2007,190: 1815-1823.

[9] 蒋尔雄,赵风光,苏仰锋.数值逼近[M].2版.上海:复旦大学出版社,2008:153-156.

[10] ORTEGA J M,RHEINBOLDT W C.Iterative solution of nonlinear equations in several variables[M].New York:Academic Press,1970:181-239.

[11] WANG H.New third-order method for solving systems of nonlinear equations[J].Numer Algor,2009,50(3): 271-282.

Uniform-coefficient Quadrature-based Iterative Methods for Solving Nonlinear Equations

YAO Tengteng
(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

Abstract:In this paper,we present a new variant of Newton's method for solving nonlinear equations based on uniform-coefficient quadrature formulas.The cubic convergence of the proposed algorithm is established.Moreover,the fifth-order convergence is proved under some mild conditions.Some numerical experiments are reported to illustrate the effectiveness and the flexibility of our algorithm.

Key words:uniform coefficient quadrature;newton-type method;nonlinear equations;cubic convergence

收稿日期:2015-05-27 录用日期:2015-11-24

doi:10.6043/j.issn.0438-0479.2016.02.013

中图分类号:O 151.23

文献标志码:A

文章编号:0438-0479(2016)02-0221-06

Email:yaotengteng718@163.com

引文格式:姚腾腾.基于一致系数求积的广义牛顿法求解非线性方程组[J].厦门大学学报(自然科学版),2016,55(2):221-226.

Citation:YAO T T.Uniform-coefficient quadrature-based iterative methods for solving nonlinear equations[J].Journal of Xiamen University(Natural Science),2016,55(2):221-226.(in Chinese)

考虑如下非线性方程组: