典型水面结构在水下爆炸作用下的毁伤模式研究*

2016-04-15张永坤

舰船电子工程 2016年3期

关键词：爆炸舰艇定理

张永坤　高　鑫

(91439部队　大连　116041)

典型水面结构在水下爆炸作用下的毁伤模式研究*

张永坤高鑫

(91439部队大连116041)

摘要论文首先给出典型水面结构在水下爆炸作用下的毁伤模型,根据能量守恒原理得到板架塑性变形能等于板架初始动能,给出板架塑性变形能计算公式。从模型参数、载荷参数及流固耦合效应等效三方面,得到相似准数中所包含的全部物理量,利用方程分析法及量纲分析法导出典型水面结构在水下爆炸作用下运动现象的相似准数;利用π定理,建立关于相似准数的准数方程式,进而得到表征结构毁伤程度的相似准数与其他准数之间的关系,最后得到能够通过模型实验预报实船结构毁伤参数的经验公式。

关键词舰艇; 结构; 毁伤; 爆炸; π定理

Damage Model of Ship Structure in Underwater Explosion

ZHANG YongkunGAO Xin

(No. 91439 Troops of PLA, Dalian116041)

AbstractShip structure anomalous dynamic model subjected underwater explosion is obtained. According to conversation of energy, the plate flexibility distortion energy equals to its initialized kinetic energy. The computation formulation of plate flexibility distortion energy is given. All physical factors of similarity number are achieved by analyzing modelparameters, loading parameters and fluid-squid coupling effect. Ship structure similarity number subjected underwater explosion is obatined using formula analysis method and mension analysis method. Based on π theory, similarity number formula is founded which shows the relationship between of similarity numbers and other factors. Finally, the experience formula is given which can predict ship structure distortion parameters using model test results.

Key Wordswarship, structure, damage, explosion, π theory

Class NumberU664.2

1引言

水下爆炸作用下典型水面结构的毁伤模式包括局部结构塑性大变形和开裂破坏,整体箱形梁结构弹塑性动态响应和塑性铰破坏,整体箱形梁结构冲击振动(鞭状运动)和塑性铰破坏等。不同毁伤模式所要研究的相似准数不同,冲击波作用下的塑性动态响应主要考虑抗弯能力和塑性变形(应变)相似,气泡脉动引起的船体鞭状运动主要考虑振动频率和应力应变相似。研究方法包括理论计算方法研究和实验研究[1~6]。

由于问题的复杂性,从理论上确定准数方程式的具体形式有所困难,故拟用数值仿真实验的方法[7~11]。在用仿真实验方法求解准数方程的时候,首先得到相似准数中所包含的全部物理量,并将仿真实验数据整理成相似准数,进而得到表征结构毁伤程度的相似准数与其他准数之间的关系,最后得到能够通过模型实验预报实船结构毁伤参数的经验公式。利用方程分析法或量纲分析法导出典型水面结构在水下爆炸作用下运动现象的相似准数;利用π定理,建立关于相似准数的准数方程式。

爆炸载荷作用在舰船板架上,冲击波作用时间与板架固有周期相比很小,因此可用动量定理求解板架初始动能。根据单位面积入射冲量可以确定船体局部板架的初始动能。

2典型水面结构在水下爆炸作用下的毁伤模型

2.1船体板架结构的毁伤模型

船体局部板架可以视为一加筋板结构,船体底部外底板仍然视为板结构,肋板和纵桁作为加强筋的腹板,船体底部内底板作为加强筋的面板。

加筋板四边为简单支撑或固定支撑。在水下爆炸冲击波的作用下,加筋板结构产生整体横向变形,在整体横向变形的基础上,局部板格也产生横向变形。所以板架的最大变形一般出现在板格中部,同样最大应变也出现在该处。

建立了船体局部板架的毁伤物理模型之后,就可以根据相似理论确定相应的相似参数,进而确定模型相似律。

图1　船体局部板架结构的毁伤模型

2.2船体局部板架结构在水下爆炸冲击作用下的能量分析

舰船板架在爆炸载荷作用下将产生较大的塑性变形,因而一般可假设舰体材料为理想刚塑性材料,弹性变形忽略不计。另外,假设舰体板架为四边固支,在爆炸载荷作用下,板架要产生较大挠度(塑性大变形),考虑到板架边界要产生塑性铰线,板架整体变形的挠曲面函数可取某一函数形式,例如为

(1)

其中:L为板架长,B为板架宽,W0为板架中心挠度。坐标xoy位于板架初始平面,如图2所示。

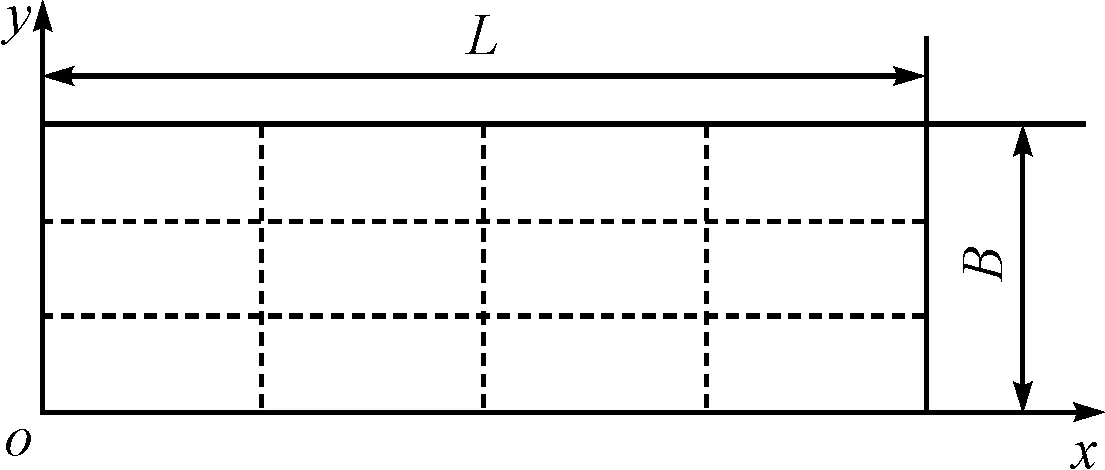
图2　板架示意图

板架在爆炸载荷作用下的塑性动力响应研究,主要是要求解板架的中心挠度W0,其求解方法可根据能量守恒建立所需方程,即:冲击波对板架作用的能量要等于板架的塑性变形能。考虑到冲击波作用时间很短,冲击波对板架的作用可按冲量来考虑,则冲击波能量将首先转化为板架初始动能K,由能量守恒原理可得板架塑性变形能U等于板架初始动能K,即:

U=K

(2)

板架塑性变形能的计算可将板架化为正交的骨架梁系来考虑,并将板架的板作为骨架的带板。板架变形能由三部分组成,即:边界塑性铰弯曲变形能U1,板架区域内的弯曲变形能U2和板架区域伸长变形能U3,即总塑性变形能为

U=U1+U2+U3

(3)

设板架沿x方向有n根骨架梁,其在y方向的坐标为yi(i=1,2,…,n);沿y方向上有m根骨架梁,其在x方向的坐标为xj(j=1,2,…,m),则板架的各项塑性变形能可分别求解如下。

2.3船体局部板架结构在水下爆炸冲击作用下的能量分析

1) 边界塑性铰弯曲变形能U1

(4)

2) 板架弯曲变形能U2

(5)

3) 板架伸长变形能U3

(6)

式中:M0i为x方向第i根骨架梁的塑性极限弯矩。M0j为y方向第j根骨架梁的塑性极限弯矩。

其中W为板架挠曲面函数,并由式(1)给出,γx、γy分别为x方向和y方向边界的固定程度系数。边界为刚性固定时,γ=1;边界完全自由支持时,板架在边界处不产生塑性铰,因而取γ=0。

4) 板架初始动能

3相关物理量的确定

在确定的条件下,船体局部板架的毁伤也是确定的。确定这些条件的物理量称为独立的物理量或自变量。标志船体局部板架的毁伤效果的任何一个参数(物理量)都仅仅是这些自变量的函数,所以都是因变量。根据量纲分析中的Π定理,如果有N个独立的物理量,就可以组成N-3个相互独立的无量纲参数,称之为相似参数。每一个表征船体局部板架毁伤效果的物理量都是因变量,可以组成一个无量纲参数,它是各相似参数的函数。

在船体局部板架受水下爆炸冲击波作用下的毁伤效应模型相似律的问题当中,如果模型和原型相应的相似参数都相等,那么由任何标志船体局部板架毁伤效应的无量纲参数也相等,这样就可以通过模型的无量纲毁伤参数得到原型的无量纲毁伤参数,进而得到原型的毁伤参数。因此保证毁伤效应相似的条件是相应的相似参数相等。得到相似参数的关键在于首先选定那些是独立的物理量。以下就模型参数(包括模型尺寸参数和模型材料参数)、载荷参数以及流固耦合效应参数三个方面分别进行讨论。

3.1模型

3.1.1模型尺寸

确定模型尺寸的参数有:局部板架长L,板架宽B,板厚h。设板架沿x方向有n根骨架梁,沿y方向上有m根骨架梁。由前面的能量分析可知弯曲M由材料屈服极限σs和骨架间距内受压和受拉部分面积形心至骨架梁中和轴的距离l1、l2确定;中面力N由材料屈服极限σs和骨架梁断面面积A确定。所以l1、l2和A也应确定为模型尺寸参数。

由此可知模型尺寸参数为:板架长L,板架宽B,板厚h,骨架数n、m,骨架梁断面面积A,骨架间距内受压和受拉部分面积形心至骨架梁中和轴的距离l、l2。A、l1和l2也可以包含在全塑性弯曲M和中面力N中。

3.1.2模型材料

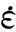
(7)

由此可知材料参数为:材料密度ρs,材料屈服极限σs,应变率强化模型参数a和b。

根据库尔的经验公式计算冲击波加载面上的冲击波载荷:

(8)

其中:p为冲击波压力,t为时间;pm为冲击波峰值压力,me为装药量,R为球面距爆心距离;α,β,k,l为经验系数。根据能量分析,冲击波作用时间与板架固有周期相比很小,因此可用动量定理求解板架初始动能。故实际上关心的是作用在船体局部板架上的冲量大小。对水下冲击波压力时程曲线进行积分即可的冲量。

由此可知表征载荷的参数实际上是冲击载荷的冲量I。

3.1.3流固耦合

基于冲击波和水中结构耦合作用的平面波近似(PWA)理论,可以得到作用在船体局部板架上的实际壁压为

(9)

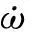
3.1.4空化

当船体局部板架相对来说较薄时,水介质中通常会出现空化。这是因为冲击波在结构上反射后在水介质里面出现了负压,于是介质就很快蒸发了,形成有液态和气态组成的空化区。为了描叙这个现象,就需要引入空化压力Pv。假设空化压力是常数,当水介质中的压力降低到-Pv时,水介质中便出现空化。由此可知,描叙空化现象的物理参数为空化压力Pv。

4几何相似律

以质量M,长度L和时间T为基本量纲,表1对各相关物理量进行了汇总,一共有17个物理量,这17个物理量均相互独立,物理意义明确,同时对各物理量进行量纲分析,表中数值表示的是对应基本量纲的指数。

由于表2中的物理量均为独立的,故如果以局部板架的最大有效塑性应变为表征其毁伤程度的物理参数,则有:

ε=f(L,B,h,m,n,Mx,My,Ny,ρs,σs,a,b,I,ρwc,Pv)

(10)

如果以外板厚度h、板架材料密度ρs和屈服强度σs为基本物理量,则式(10)可以化为无量纲形式:

(11)

式(11)中各无量纲参数即为相似参数,共有13个,各相似参数的物理意义也是比较明确的:L/h为板架长与板厚之比;B/h为板架宽与板厚之比;m和n为加强筋个数;M/σsh3为板架梁塑性极限弯矩和外板塑性极限弯矩之比;N/σsh2为板架梁塑性极限中面力和外板的塑性极限中面力之比;ρsa2h2/σs和b表示材料特性;I2/ρsσsh2表示冲击波入射压力和板结构变形阻力之比;(ρωc)2/ρsσs表示流固耦合作用;PV/σs为空化压力与板架材料屈服强度之比。要使得模型与原型的最终有效塑性应变相同,需要使得原型和模型在式(11)中的各相似参数相等。以下以角标m代表模型,以角标p代表原型具体进行分析。

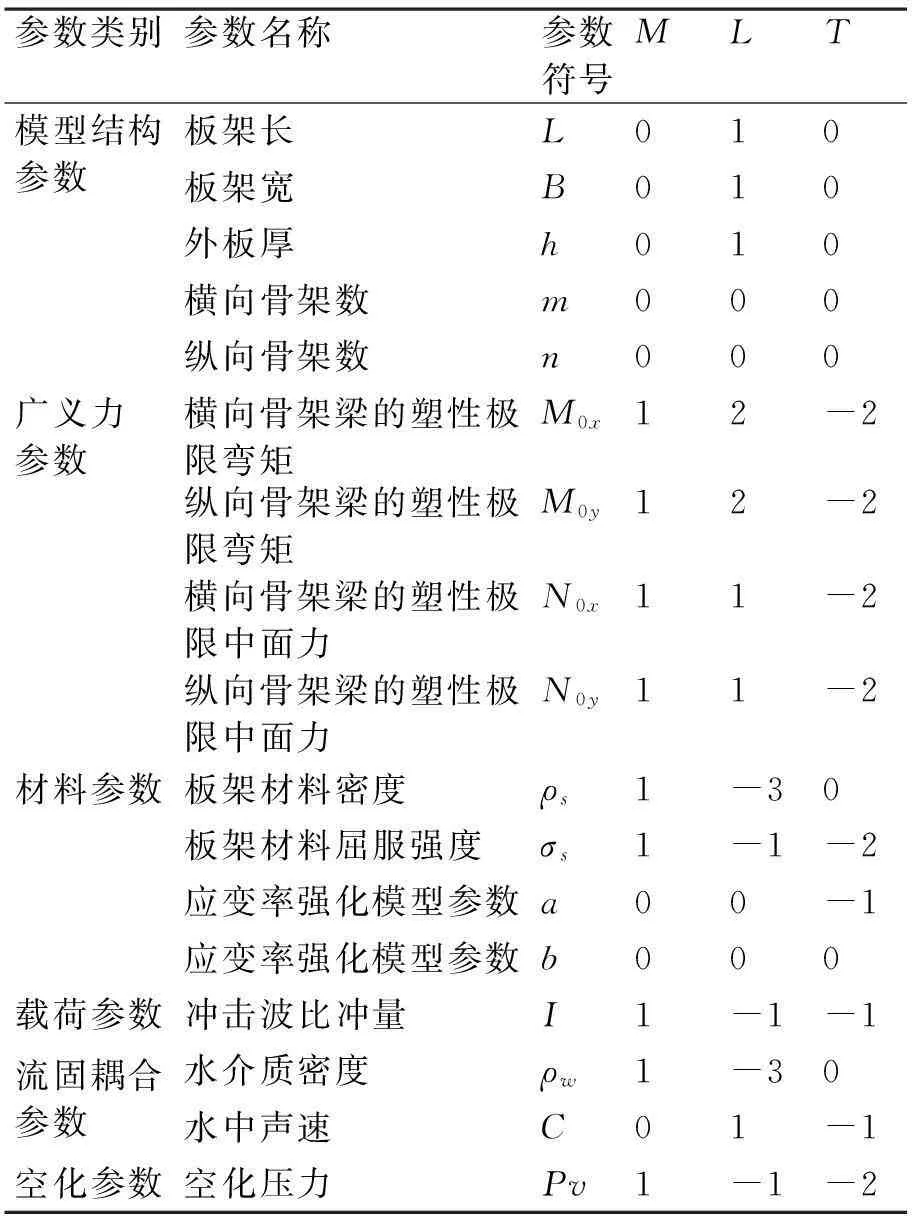
表1　各物理量汇总及量纲分析

式(12)表示原型和模型在长、宽和外板厚上是几何相似的,这一点在进行模型试验时是比较容易实现的。

(12)

式(13)表示原型和模型在横向和纵向的加筋数目是相等的,这一点在进行模型试验时也是比较容易实现的。

mm=mp,nm=np

(13)

定义M0=σsA(l1+l2)/2,所以如果模型的外板和加强筋能够保证与原型几何相似,同时模型和原型采用相同的材料,即屈服强度相同,则式(14)自然成立。

(14)

定义N0=σsA,所以如果模型的外板和加强筋能够保证与原型几何相似,同时模型和原型采用相同的材料,即屈服强度相同,则式(15)也自然成立。

(15)

由式(16),如果模型和原型的材料相同,即ρs、σ式s和a相同,则要求原型和模型的板厚相同,此相似参数才相同。在进行模型试验时满足这个条件是非常困难的,因为一般来说,模型相对于原型来说都是要进行几何缩比的,而这一条件要求模型和原型在板厚上完全相同。如果同时满足式(12)的条件,那么实际上要求模型和原型完全相同,这样就失去了进行模型试验的实际意义。所以式(15)的相似参数相同是进行船体局部板架在水下爆炸冲击波作用下的模化试验的主要障碍之一,需要进行进一步研究。

(16)

如果原型和模型的材料相同,则材料的应变率强化模型参数也是相同的,故式(17)自然满足。

bm=bp

(17)

式(18)是表征水下爆炸冲击载荷的相似参数相同,如果模型和原型的材料相同,即ρs、σs相同,则只要求原型和模型的入射冲量之比为模型和原型的几何缩比,即可满足式(18)。

(18)

由于模型和原型均在水中进行爆炸试验,故ρsc相同。如果原型和模型采用相同的材料,则ρs、σs相同。所以式(19)也自然满足:

(19)

近似认为水的空化压力为一常数,如果原型和模型采用相同的材料,则式(20)也自然满足。

(20)

根据对各相似参数的分析可以看到,如果模型和原型采用相同的材料,且满足几何相似,则模型和原型的13个相似参数中有12个相同。而式(16)表示的相似参数相同,则要求模型和原型在板厚上相同,这一点是比较困难的,需要进行进一步的研究。如果原型和模型所采用的材料为应变率不敏感材料,则该相似参数对待定参数的影响很小,可以忽略不计,这样模型和原型就可以满足几何相似律,但如果材料为应变率敏感材料,则模型试验结果需要进行修正才能换算到原型上去。

5结语

根据以上分析,可以得到模型化研究方法的技术路线,归纳如下:

1) 对水面典型结构的在水下爆炸冲击作用下的毁伤模式进行分析,方法可以通过数值仿真或者试验结果;

2) 根据1)中提出的毁伤模式,建立对水面典型结构的在水下爆炸冲击作用下的毁伤物理模型;

3) 根据毁伤物理模型,通过能量原理或建立运动微分方程等理论方法分析水面典型结构的在水下爆炸冲击作用下的变形机理,提出相关物理量参数;

4) 根据相似定律,对相关物理量进行量纲分析,得到各无量纲相似参数;

5) 对各模型和原型的各相似参数进行分析,提出满足相似的试验方法;

6) 对于模型和原型无法实现相等的相似参数,可以采用变换基本物理量纲的方法使得相似参数相等,如果仍然无法满足,则可以提出相应的修正方法,从而使得模型的试验结果可以推换到原型上。

参考文献

[1] 张振华.舰艇结构在水下爆炸作用下损伤响应的相似预报方法研究[D].武汉:华中科技大学,2009.

[2] 刘建湖.舰船非接触水下爆炸动力学的理论与应用[D].无锡:中国船舶科学研究中心,2002.

[3] 朱锡,张振华,梅志远,等.舰船结构毁伤力学[M].北京:国防工业出版社,2013.