基于ENN和UKF的电子部件剩余使用寿命预测*

李文峰　许爱强　尹　晋　朱广辉

(1.海军航空工程学院科研部　烟台　264001)(2.92635部队　青岛　266000)



基于ENN和UKF的电子部件剩余使用寿命预测*

李文峰1,2许爱强1尹晋2朱广辉2

(1.海军航空工程学院科研部烟台264001)(2.92635部队青岛266000)

摘要针对部分可观测信息条件下量测噪声未知时非线性滤波剩余寿命预测的问题,提出了一种基于集成神经网络(ENN)和无迹卡尔曼滤波(UKF)的寿命预测方法。首先,结合设备性能退化量测数据,生成状态-观测数据组,并利用bootstrap技术构建多个数据组,采用集成神经网络训练状态-观测数据组,根据推导公式估计量测噪声标准差的最优取值范围;其次,将量测噪声标准差作为未知参数嵌入在无迹卡尔曼滤波寿命预测框架中,实现非线性系统的剩余寿命预测及概率密度分布;最后,选取电子部件锂电池进行寿命预测仿真验证了该方法的有效性和可行性。

关键词无迹卡尔曼滤波; 集成神经网络; 剩余使用寿命预测; 锂离子电池

Residual Useful Life Prediction for Electronic Component Based on ENN and UKF

LI Wenfeng1,2XU Aiqiang1YIN Jin2ZHU Guanghui2

(1. Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai264001)

(2. No. 92635 Troop, of PLA, Qingdao266000)

AbstractA new method based on the methods of ensemble neural networks and unscented Kalman filter is proposed for predicting the residual useful life based on the unscented Kalman filter with unknown measurement noise under the condition of partially observable information. Firstly, in combination with the equipment performance degradation data, a state of the group of observed data is generated, and the bootstrap technique is used to construct of a plurality of groups of data, the integrated neural network training state observation data sets are adopted to estimate the measurement noise optimal range according to the formula. Secondly, the residual life prediction and probability density distribution of the nonlinear system are realized by embedding the standard error of measurement noise as the unknown parameters into the framework of unscented Kalman filter lifetime prediction. Finally, the validity and feasibility of the proposed method is verified by the simulation of the life of the lithiumion battery.

Key Wordsunscented Kalman filter, ensemble neural networks, residual useful life prediction, lithium-ion battery

Class NumberTN607

1引言

精确的设备剩余使用寿命(Remaining Useful Life,RUL)预测是维修决策的前提,现实条件下,设备或部件通常表现为非线性系统,且因噪声干扰、检测误差及信息不完备导致的不确定性会影响设备或部件的状态估计或RUL预测。能够处理非线性系统的无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法广泛应用于状态估计、RUL预测、目标跟踪及组合导航等领域[1~6],文献[7]基于一种根据SOC及电流计算库仑效率的方法,采用用自适应无迹卡尔曼滤波算法预测电池SOC;文献[8]针对水下航行器连续非线性控制系统的故障诊断问题,通过采用改进的连续-离散无迹卡尔曼滤

波算法,估计故障数据;文献[9]研究了一种融入高斯过程回归的改进平方根无迹卡尔曼滤波方法,建立发动机气路部件状态监控模型;文献[10]针对设备状态呈现非线性变化以及工程实际中的实时性寿命预测要求,提出一种基于无迹卡尔曼滤波的在线剩余寿命预测方法;文献[11]基于电池的内阻模型,采用基于无迹卡尔曼滤波算法实现非线性条件下锂电池SOC和SOH的估算。

上述文献使用UKF算法时一般是在给定量测噪声的情况下实现状态估计或RUL预测,然而,现实应用中,量测噪声通常难以求得,这就要求我们寻求一种方法求得量测噪声的分布,利用状态数据和量测数据构建数据对,采用稳定性较好的集成神经网络(Ensemble Neural Network,ENN)训练bootstrap技术生成的多组数据对,然后根据推导公式计算出量测噪声的分布为零均值高斯噪声分布的方差最优范围,在确定了方差的初始范围后,将其作为未知参数,带入到UKF算法框架中,通过已知量测数据的状态跟踪确定未知参数的取值,最后,在确定了未知参数的基础上,实现UKF剩余使用寿命预测及概率密度分布。

2无迹卡尔曼滤波原理介绍

2.1问题描述

电子设备的退化过程是指设备或部件的性能随工作时间不断劣化的过程。在表征设备或部件性能退化程度上,有两种可选择的参数,一种是能够直接或间接表征设备状态退化的状态参数如电压、电流等,另一种参数是设备的使用环境如温度、振动等时间应力。通过选择某种参数建立系统退化模型,评估系统状态及预测系统剩余使用寿命,从而确定维修间隔期。但不论选择何种参数建立系统的物理损伤模型计算设备或部件的累计损伤,都会受到噪声的污染,还有模型建立、数据监测过程中产生的不确定性[12~13]等,都会严重影响状态估计及剩余使用寿命预测的精度。

考虑一个非线性系统,定义向量表征在离散的时间步骤tk=kΔt时的系统状态,而下列状态空间模型描述了向量的演化:

(1)

式(1)中,fk:Rnx×Rnω=Rnx,状态转移函数(可能是非线性的);{ωk,k∈R}是一个独立同分布的状态噪声的已知分布向量序列;hk:Rnx×Rnv=Rnz,量测函数(可能是非线性的);{vk,k∈R}是一个独立同分布的状态噪声的已知分布向量序列。

因而,假设量测{zk,k∈R}与给定的由一阶马尔科夫模型描述的状态过程{xk,k∈R}是条件独立的。

2.2UKF基本原理

UKF[14]采用一种被称为UT变换的方法对一二阶矩进行拟合,该算法的提出并没有详细的理论依据,只是出于近似概率分布比近似非线性方程更容易的考虑,该算法有了一系列的完善,主要有两个方面的改进:

1) UT变换

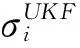
(2)

2) 采样点选取方法

UKF的采样点选取需满足如下条件:

(3)

其中,关于权值的条件,并不需要像粒子滤波将权值限定在[0,1],可以任意取值,只需满足加权和等于1即可。

给出的采样点如下:

(4)

与采样点相对应的权值为

(5)

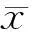
针对非局部效应的问题,即采样点离中心点的距离会随着维数的增加而增大,Julier提出了比例修正采样:

(6)

参数α>0,用于调节采样点到中心点的距离,其权值为

(7)

协方差计算公式为

(8)

对κ进行修正,修正后的比例参数λ为

λ=α2(n+κ)-n

(9)

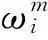
(10)

(11)

通常,参数α、β和κ的调整需要依据具体的实际应用问题来实现。

3基于集成神经网络的量测噪声方差估计

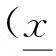
假设量测模型可以表示为

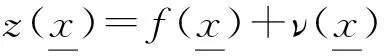
(12)

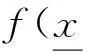
(13)

经验研究已经表明集成方法是一个简单稳定的方法,可以提高训练的准确度。

(14)

3.1模型误差分布的方差

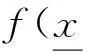
(15)

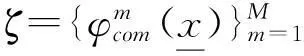
(16)

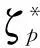
(17)

最后,上述方法得到的回归分布估计为

(18)

3.2量测噪声分布

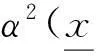
对式(14)两边同时求方差得到:

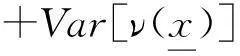
(19)

(20)

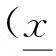
4实例分析

在介绍了上述方法后,选择实例来验证算法的有效性,选取电子部件—锂离子电池,即文献[21]中的锂电池作为研究对象,电池容量作为反映电池退化特征的指标,其退化模型为

λ=aexp(-bt)

(21)

其中,a和b为模型参数,t为时间,λ为表示电解质阻抗RE或转移阻抗RCT的内在电池性能。

假设a的真实值为1,b的真实值为0.012,根据公式迭代计算电池容量的真实值,在容量真实值中加入高斯噪声ε∽N(0,0.052)。参数的真实值只被用于产生量测数据。然后,预测的目的是根据数据估计参数σ。状态空间模型为

xk=exp(-0.012×Δt)xk-1

(22)

其中,tk=tk-1+Δt。在这种情况下,由于状态方程中含有模型参数,通过模型参数的不确定性过程噪声vk能够被处理,所以选择忽略过程噪声。量测方程为

zk=xk+ωk,ωk∽N(0,σ)

(23)

量测数据的采集周期是5个周,量测历史数据如表1所示。

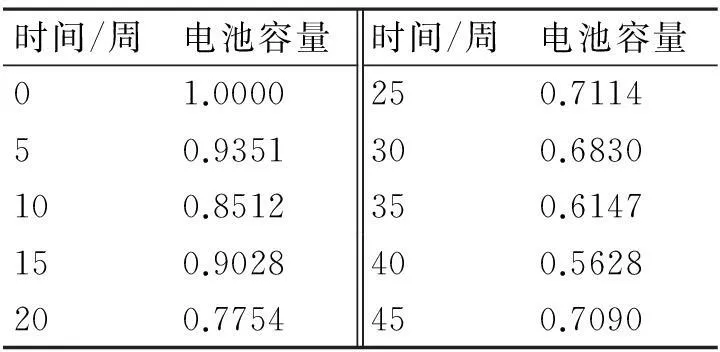
表1　量测历史数据

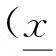
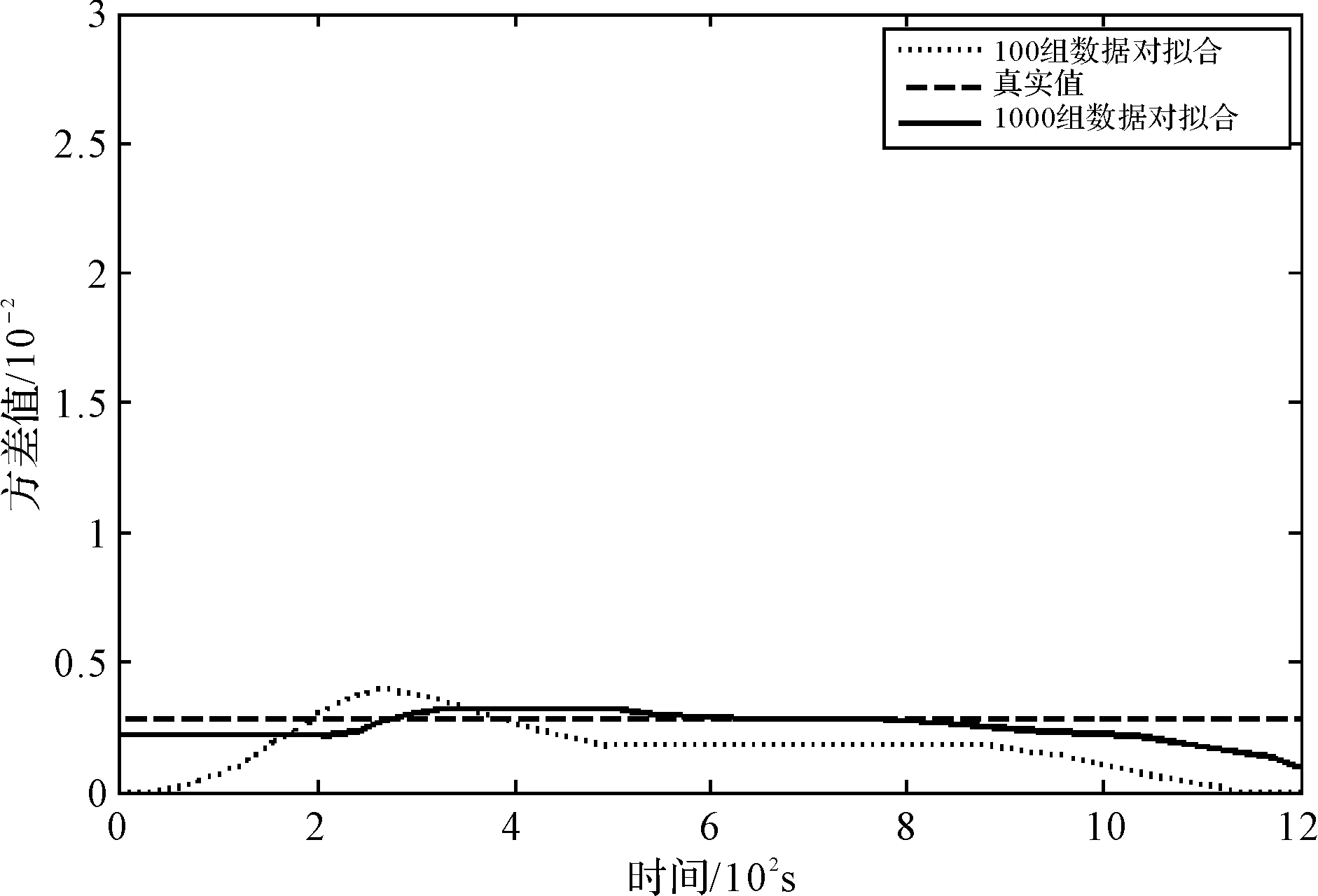
图1　不同数量的训练数据下量测噪声方差近似拟合

经上述分析可知,未知的参数变为Θ=[x,σ]T。锂电池失效的容量阈值为电池容量的30%,即0.3Ah,量测信息数据共10个样本点,预测的初始起点为锂电池容量周期T=45周,45周之前为量测历史数据,从第45周开始,运用UKF算法,预测每个周期的锂电池容量,根据45周之前的已知电池容量数据进行状态跟踪,估计出未知参数,量测误差方差的估计值为0.0026。

确定了经验模型中的未知参数后,UKF框架中的状态方程和量测方程就完全建立起来了,将所求参数的取值代入式(22)和式(23)中,设置好算法中所需的初始参数,粒电池容量状态初始值为1Ah,从T=45周开始执行UKF算法,迭代计算不断更新锂电池容量的状态值,随时间每5个周都输出一个新计算的容量值,在此迭代过程中持续判断电池容量值是否达到或超出其容量阈值,如达到或超出,则终止计算过程,最后,基于UKF的锂电池RUL预测及概率密度分布如图2和图3。

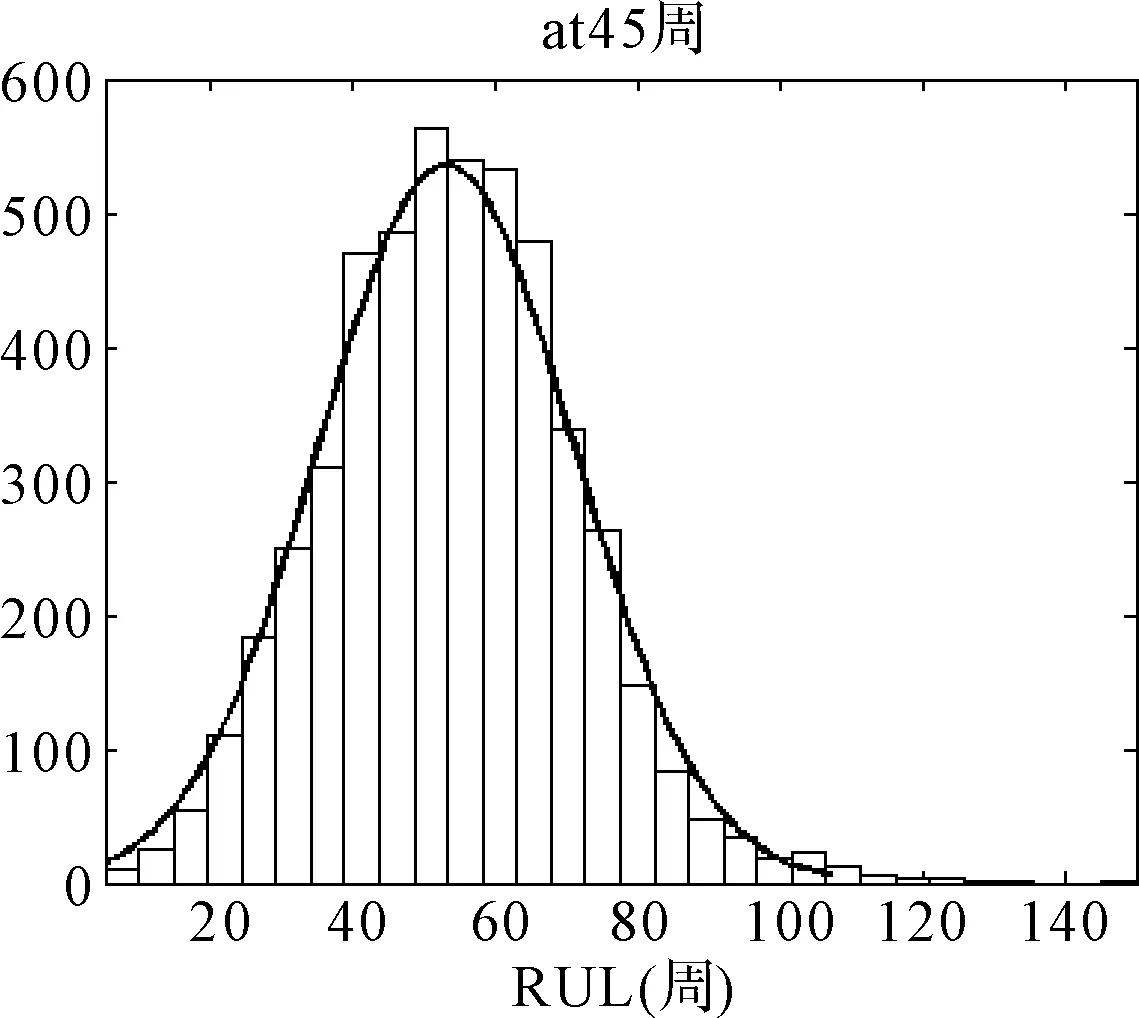
图2　剩余使用寿命的概率密度分布

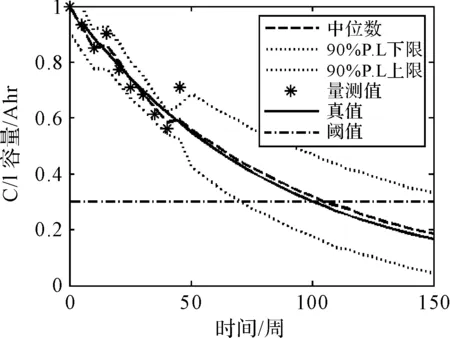
图3　电池容量退化监控与预测

5结语

通过实例验证分析,可以看出,在建立电子设备或部件的物理损伤经验模型后,针对UKF在预测电子设备剩余寿命时,状态空间模型中的状态噪声和量测方程中的量测噪声往往难以确定的问题,首先,在状态方程中引入一个未知参数,将状态噪声引起的不确定性转化成模型参数的不确定性,其次,利用集成神经网络算法求取量测噪声分布最优范围,利用将监测到的状态退化数据作为先验信息,对未知参数进行状态跟踪,结合锂电池量测历史数据,利用UKF算法对电子设备或部件的真实状态进行估计,从而预测电子部件的剩余使用寿命,在此过程中,UKF算法能够消除一系列不确定性因素,并给出剩余使用寿命的概率密度分布,从而保证了锂电池容量剩余使用寿命预测的精度。

参 考 文 献

[1] 张勇刚,黄玉龙,武哲民,等.一种高阶无迹卡尔曼滤波方法[J].自动化学报,2014,40(5):838-848.

[2] 张园,郭晨,李树军,等.机动目标跟踪的S修正无迹卡尔曼滤波算法[J].大连海事大学学报,2015,41(2):84-86.

[3] 潘加亮,熊智,王丽娜,等.一种简化的发射系下SINS/GPS/CNS组合导航系统无迹卡尔曼滤波算法[J].兵工学报,2015,36(3):484-491.

[4] 赵治国,杨杰,陈海军,等.四驱混合动力轿车驱动工况无迹卡尔曼车速估计[J].机械工程学报,2015,51(4):96-107.

[5] Valverde G, Terzija V. Unscented Kalman filter for power system dynamic state estimation[J]. IET generation, transmission & distribution,2011,5(1):29-37.

[6] Al-Hussein A, Haldar A. Novel Unscented Kalman Filter for Health Assessment of Structural Systems with Unknown Input[J]. Journal of Engineering Mechanics,2015,5(4):12-15.

[7] 李司光,张承宁.锂离子电池荷电状态预测方法研究[J].北京理工大学学报,2012,3(2):22-30.

[8] 徐德民,刘富樯,张立川,等.基于改进连续-离散无迹卡尔曼滤波的水下航行器故障诊断[J].西北工业大学学报,2014,32(5):756-760.

[9] 胡宇,杨月诚,张世英,等.基于改进平方根无迹卡尔曼滤波方法的涡扇发动机气路状态监控[J].航空动力学报,2014,29(2):441-450.

[10] 林国语,贾云献,孙磊.基于无迹卡尔曼滤波的直升机主减速器剩余安全寿命预测[J].机械传动,2015(5):98-101.

[11] 陈宁,胡小军,桂卫华,等.基于无迹卡尔曼滤波的锂电池SOC和SOH的估算方法[C]//第26届中国控制与决策会议论文集,2014.

[12] 孙强,岳继光.基于不确定性的故障预测方法综述[J].控制与决策,2014,29(5):769-778.

[13] 许喆平,郎荣玲,邓小乐.飞机性能参数预测的不确定处理[J].航空学报,2012,33(6):1100-1107.

[14] Wan E, Van Der Merwe R. The unscented Kalman filter for nonlinear estimation[C]//Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. AS-SPCC. The IEEE 2000. IEEE,2000:153-158.

[15] J. Carney, P. Cunningham, U. Bhagwan. Confidence and prediction intervals for neural network ensembles[C]//International Joint Conference on Neural Networks, IJCNN’99, Washington, DC, 10-16 July,1999:1215-1218.

[16] D. Nix, A. Weigend. Estimating the mean and the variance of the target probability distribution[C]//Proceedins of IEEE International Conference on Neural Networks, World Congreson Computational Intelligence, vol.1, Orlando, FL, 27 June-02 July,1994:55-60.

[17] A. M. Zoubir, B. Boashash. The bootstrap and its application[J]. IEEE Signal Processing Magazine,1998,1:56-76.

[18] Deng N, Allison J J, Fang H J, et al. Using the bootstrap to establish statistical significance for relative validity comparisons among patient-reported outcome measures[J]. Health Qual Life Outcomes,2013:11-89.

[19] P. Baraldi, M. Compare, S. Sauco, et al. Ensemble neural network-based particle filtering for prognostics[J]. Mechanical System and Signal Processing,2013,41:288-300.

[20] Zhou Zhihua, Wu Jianxin, Tang Wei. Ensembling neural networks: Many could be better than all[J]. Artificial Intelligence,2002,137:239-263.

[21] Dawn An, Joo-Ho Chio, Nam Ho Kim. Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab[J]. Reliability Engineering and System Safety,2013,115:161-169.

中图分类号TN607

DOI:10.3969/j.issn.1672-9730.2016.03.028

作者简介:李文峰,男,博士研究生,研究方向:航空装备故障预测与综合保障。许爱强,男,教授,博士生导师,研究方向:自动测试与装备综合保障。

基金项目(编号:9140A27020214JB14436)资助。

收稿日期:2015年9月3日,修回日期:2015年10月26日基金项目:总装武器装备预研