基于遗传算法的稳定平台控制系统研究*

李　昂　李　楠　高　远　郭　斌

(1.海军驻天津地区军事代表局　北京　100073)(2.海军工程大学导航工程系　武汉　430033)



基于遗传算法的稳定平台控制系统研究*

李昂1李楠1高远1郭斌2

(1.海军驻天津地区军事代表局北京100073)(2.海军工程大学导航工程系武汉430033)

摘要陀螺稳定技术是重力测量领域的一项重要技术,而高精度旋转控制是其核心技术之一。PID控制技术凭借其可靠性好、可行性强等优势在目前的工业控制领域占有重要地位。但是传统PID控制系统存在快速性和准确性的矛盾。为了解决陀螺稳定平台PID控制过程中的这一矛盾,并考虑到重力测量稳定平台的特殊控制需求,研究了一种基于遗传算法的稳定平台自适应控制算法。仿真实验结果表明,相对与传统PID控制系统,论文提出的算法具有小冲击、动态过程好、鲁棒性好等优势。

关键词重力测量; 陀螺稳定平台; PID; 遗传算法

Stable Platform Control System Based on Genetic Algorithm

LI Ang1LI Nan1GAO Yuan1GUO Bin2

(1. Navy Representative Bureau in Tianjin, Beijing100073)

(2. Department of Navigation, Naval University of Engineering, Wuhan430033)

AbstractGyroscope based stabilized platform is an important instrument in the field of gravity measurement. And high precision rotary control technology is one of the core technologies of stabilized platform. PID control system plays an important role in the field of industrial control for its reliability and feasibility. But, there exists a contradiction between rapidity and accuracy in the traditional PID control system. In order to compromise the contradiction in the stabilized platform system, considering the special requirements for gravity measurement stabilized platform control, a genetic algorithm based adaptive control method for the the stabilized platform is proposed in this paper. Simulation experimental results show that compared with traditional PID control system, the proposed algorithm owns the advantages of low strikes,good robustness and good dynamic process.

Key Wordsgravity measurement, stabilized platform, PID, genetic algorithm

Class NumberTP273

1引言

稳定平台式重力仪是大地重力场测量的一种重要仪器[1~3],陀螺稳定平台是其中必不可少的组成部分。稳定平台的主要功能是提供高度稳定的水平基准和姿态信息,以保证重力传感器在工作中始终保持稳定的垂直指向,消除运动载体姿态变化带来的测量误差,隔离振动等干扰因素对重力测量的影响。有效、可靠的控制策略是保证平台稳定精度的的必要条件,因此对稳定平台控制策略的研究具有重要的现实意义。

重力测量陀螺稳定平台的工作原理如图1所示。

图1　重力测量稳定平台工作原理

与平台台面固连的惯性测量组件(Inertial Measurement Unit,IMU)检测平台的姿态、角速率等,将其传输给控制系统。上位机对IMU的数据进行显示、保存,并将相关数据输入至控制器,控制器将IMU的姿态、角速度等信号作为控制回路的输入信号,经过解算,输出控制信号驱动俯仰和横滚力矩电机转动,从而使平台保持水平。平台的姿态或角速率的变化又会反馈给IMU从而形成控制闭环。

在控制策略方面,PID作为一种经典的控制策略,已在工业控制中得到了广泛应用。PID控制器目前仍是控制领域最普遍、最可靠的控制器[4~5]。但是,传统PID控制系统存在快速性和准确性的矛盾。为了解决这一矛盾,实现稳定平台高精度稳定控制,本文研究了一种基于遗传算法的稳定平台自适应控制策略。仿真研究表明,该算法能够实现稳定平台的平稳启动及高精度稳定控制。

2控制系统建模

如图1所示,本系统是两轴两框架结构。下面以单轴稳定系统为例,控制回路的结构如图2所示。本系统为了保证控制精度和刚度,采用位置环和速度环的双环控制,位置环也称外环,速度环也称内环。

图2　单轴控制回路结构示意图

根据图2中控制系统的结构,对其进行控制系统建模。忽略电机反电势电压的影响,直流力矩电机的传递函数可以表示为

(1)

式中,Rωta为直流力矩电机的输出扭矩,Cm为力矩电机力矩常数,La为电机电枢电感,Ra为电机电枢电阻,Uc为加在电枢两端的电压。

本系统中电枢电感La远小于电枢电阻Ra。因此,本系统中,力矩电机模型可以简化为

(2)

电机轴上的力矩平衡方程可以表示为

(3)

式中,M为电机轴上的输入力矩,Mf为电机轴上的摩擦力矩,J为旋转体的转动惯量,ω为旋转体的旋转角速率。

上式可以同样表示为

(4)

式中,f为电机轴上的粘滞阻力系数。

因此,旋转体的传递函数可以表示为

(5)

已知系统力矩电机及旋转体参数如下:电机力矩常数:Cm=3.292N·m/A;电枢电阻:Ra=2.65Ω;旋转体转动惯量为:J=1.185kg·m2;粘滞阻力系数为:f=0.00004。

于是,可得直流力矩电机的传递函数和旋转体的传递函数分别为

(6)

(7)

因此,控制系统数学模型如图3所示。

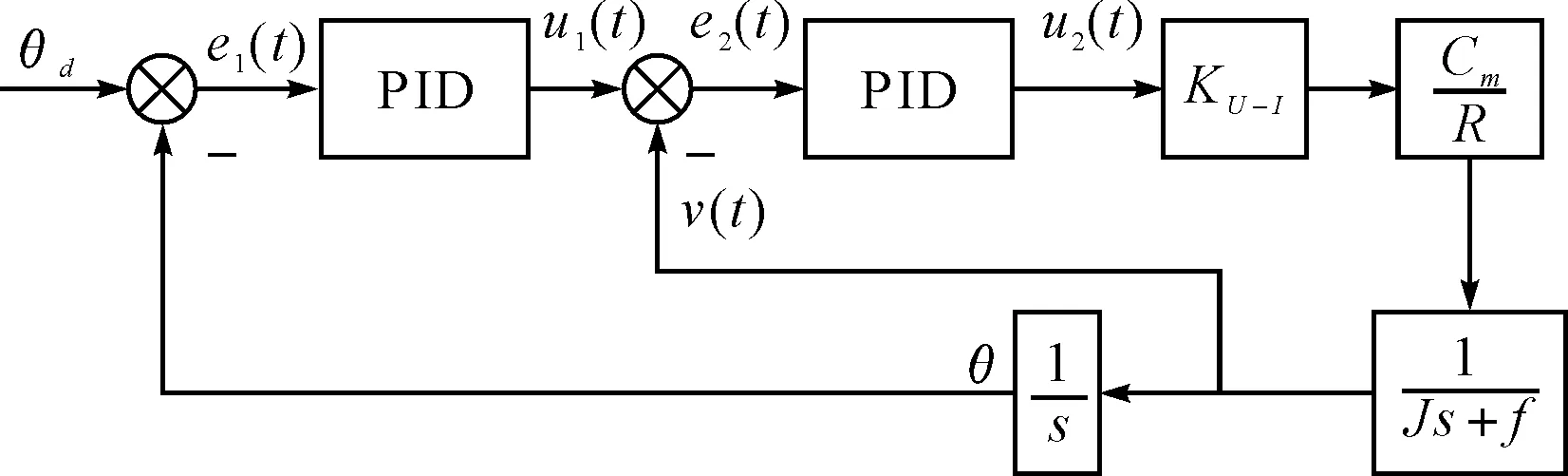
图3　控制系统数学模型

如上图所示,平台稳定基准θd与IMU输出角度θ作差得到控制位置环的控制误差e1(t),位置环控制器输出u1(t)与速度环输出v(t)作差得到速度换的控制误差e2(t),速度环控制器输出u2(t)控制被控对象,速度环输出v(t)经积分环节得到位置环的输出θ。

由控制系统数学模型可以得到,被控对象的传递函数为

(8)

式中,KU-I为放大器的放大倍数,且KU-I=6.36。

则有:

(9)

3传统PID算法及参数整定

PID参数整定是指通过调整PID控制器的参数,使得由控制对象、控制器等组成的控制回路的动态性能、稳态性能满足期望的指标要求,达到理想的控制目标。目前常用的常规PID整定法有ZN经验法、ZN临界比例度法、特征面积法、继电器自整定法等,其中ZN临界比例度法是应用最为广泛的一种整定方法。

临界比例度法的PID控制器可表述如下

(10)

其中,δ表示比例度,e表示控制偏差,TI表示积分时间系数,TD表示微分时间系数。

调节参数的步骤如下:在闭环的情况下,系统在比例环节作用下给系统加入一个小扰动,如果系统的响应是衰减,则减小比例度,反之则增加比例度,直至闭环系统做临界等幅周期振荡,此时的比例度称为临界比例度,记为δr,其振荡周期称为临界振荡周期,记为Tr。

根据经验公式可以确定系统的积分时间系数和微分时间系数,如表1所示。

表1　临界比例度法PID参数

对速度环,临界振荡周期为Tr=0.002s。为了保证速度环的稳定性,该环中采用PI控制器。因此,由表1可得,速度环的开环传递函数为

(11)

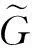
(12)

位置环的临界振荡周期为Tr=0.006s。由式(12)可以推出,在位置环PID控制器作用下,系统的开环传递函数为

(13)

其中,KP1=660.9385,KI1=220312.8442,KD1=0.5155。

利用整定得到的参数进行控制,系统对单位阶跃信号的响应曲线如图4所示。

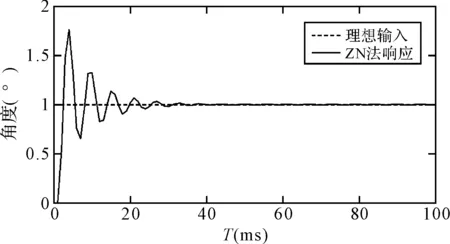
图4　基于临界比例度法的外环控制回路单位阶跃响应

根据上述仿真结果,可以看出,传统ZN临界比例度参数整定方法可以整定出适当的PID参数,使系统在阶跃输入下较快地达到稳定,稳态精度高。但是为了进一步挖掘控制系统的精度潜力,从而为保证平台稳定精度提供有力支撑,本文利用遗传算法对PID参数进行优化,以期能够达到更快速、更准确的控制效果。

4基于遗传算法的自适应控制策略研究

4.1基于遗传算法的参数整定算法

遗传算法作为一种全局优化算法,在生产生活的各个领域得到了越来越广泛的应用[7~10]。本文将遗传算法与PID控制结合起来,利用遗传算法对PID的三个系数进行整定,以得到理论上最优的PID参数。

利用遗传算法优化KP、KI、KD的具体步骤如下:

1) 确定被控对象。式(9)描述了内环的被控对象,式(12)描述了外环的被控对象。

2) 确定每个参数的大致范围和编码长度,进行编码。对KP1,KI1,KD1,KP2,KI2,KD2进行长度为20位的二进制编码。

3) 随机产生n个个体构成初始种群。本文使用的样本个体数n=50。因此,初始种群是由系统随机产生的50个60位的二进制编码。

4) 代价函数和适配函数的确定。控制系统的优劣主要由三个方面决定,即准确性、快速性和稳定性。为了消除控制量与响应之间的误差,将误差量作为约束条件的一项;为了保证控制系统良好的动态性能,需要调节时间尽可能短,因此将调节时间作为约束条件的一项;过短的调节时间可能导致控制量很大,实际系统中可能导致系统失稳,因此将控制量作为约束条件的一项。基于此,将系统代价函数定义如下

(14)

式中,e(t)为系统误差;u(t)为控制器输出,也就是被控对象的控制量;tu为上升时间;w1,w2,w3为权值系数。根据本系统对各个控制量、控制误差和上升时间的要求,经过反复调试,确定权值系数的值分别为:w1=0.999,w2=0.001,w3=2。

为了避免超调,采用惩罚功能。一旦产生超调,将超调量作为代价函数的一部分,此时,代价函数的表达式为

(15)

式中,w4是权值。经过调试,确定该权值系数为:w4=100。取适配函数为f=1/J。

5) 遗传算法的操作。遗传算法的基本操作为:复制、交叉及变异。本文中,交叉概率取为Pc=0.9。变异概率取为Pm=0.033。

6) 重复4)、5)步直到达到规定的进化代数,本文设置的进化代数为200代。

首先,利用遗传算法对内环PID参数进行整定。结果为:KP2=121.0525、KI2=29.9552、KD2=0。然后,利用遗传算法整定外环PID的参数值。遗传算法整定得到的最优参数为:KP1=639.8876、KI1=144980、KD1=1.4208。这组参数对应的PID控制器对外环被控对象的控制效果如图5所示。

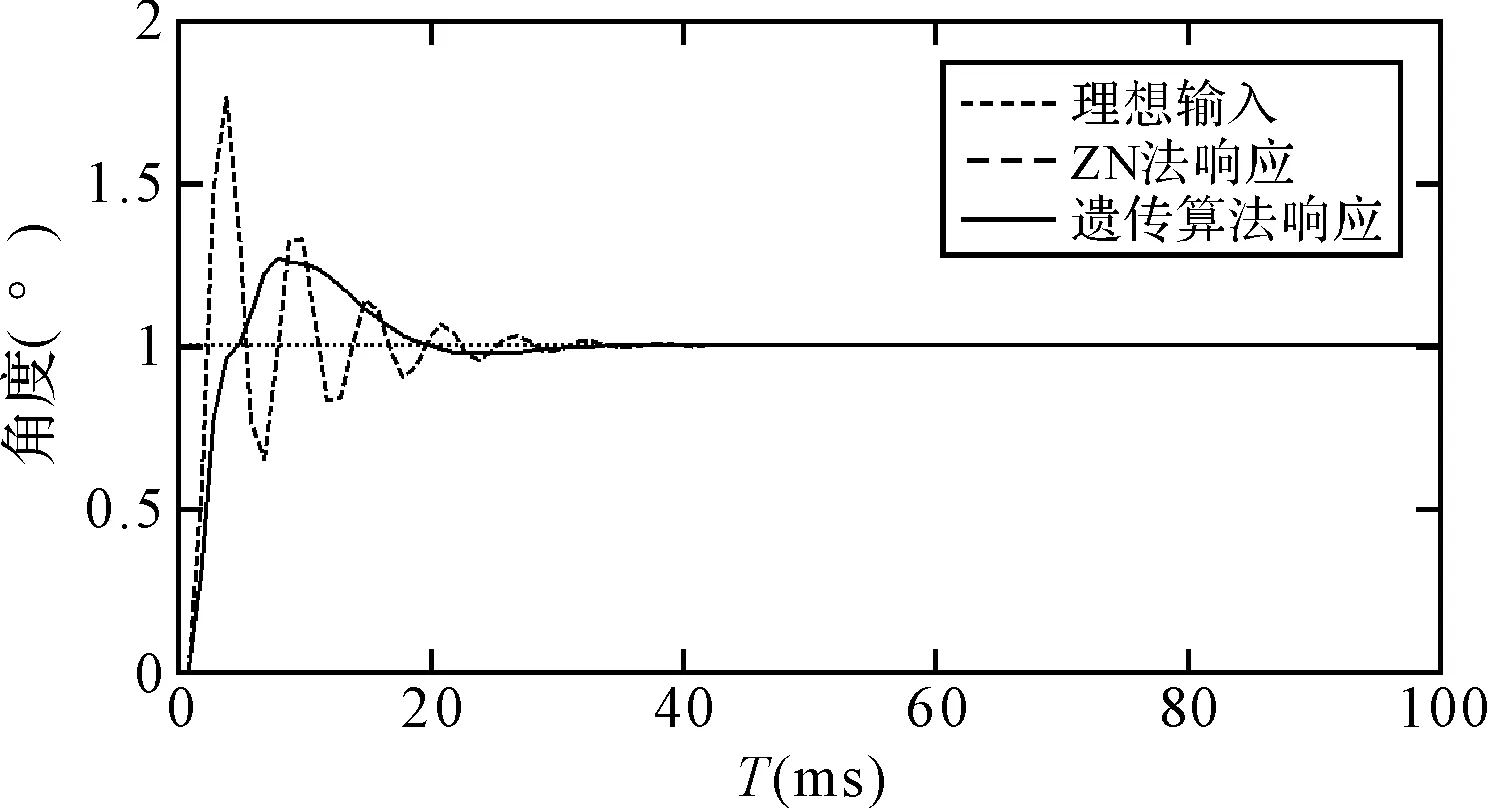
图5　基于遗传算法的外环控制回路单位阶跃响应

如图5所示,当给外环系统输入一个单位阶跃信号,利用遗传算法整定出的PID参数的控制效果同样明显优于临界比例度法整定出的PID参数所取得的控制效果。

4.2基于遗传算法的自适应PID控制算法

上节中的仿真结果表明,利用遗传算法整定出的PID参数对应的控制器的控制效果远远优于传统ZN法整定出的参数所对应的控制器。其优势主要体现在,调节时间短,动态性能好,超调量较小。这些优势有利于在平台产生小偏角或运动趋势时使平台系统快速稳定到零位,但是,当系统在大偏角下启动或系统由于异常产生大偏角的情况下,由于控制系统的调节时间很短,平台台面会经历一个剧烈调整的过程,这个过程必然会对系统产生极大的冲击,影响重力仪、光纤IMU、电机等器件的使用寿命。如果系统采用单一参数的PID控制器,这种由控制引起的冲击是不能避免的。基于此,本文提出了基于遗传算法的自适应PID控制算法。根据平台不同偏角情况下,控制系统的不同需求,建立不同的适应值函数表达式,通过遗传算法整定出不同的PID参数,进而用不同参数的PID控制器对系统进行控制。在角度在大偏角和小偏角之间切换时,PID也相应地进行切换。

本文根据稳定平台系统的实际需求,定义理想位置和实际位置的角度差小于或等于2°为小偏角,大于2°为大偏角。

在平台小偏角情况下,可以使用4.1节中建立的适应值函数,通过遗传算法来整定PID参数。这样,可以取得较好的控制效果又不至于对系统产生过大冲击。在大偏角情况下,则需对适应值函数进行重新设计。

因此,为了达到良好的控制效果,同样将控制量、控制误差和上升时间作为约束条件。与上节中建立的函数不同之处在于,在大角度下,要求调节时间在一定程度上越长越好,因此,将系统代价函数定义如下

(16)

式中,个变量的定义与上节中相同。根据本系统对各个控制量、控制误差和上升时间的要求,经过反复调试,确定权值系数的值分别为:w1=0.0000999,w2=0.0001,w3=100。

为了避免超调,同样采用惩罚功能,将超调量作为代价函数的一部分,此时,代价函数的表达式为

(17)

式中,w4是权值。经过调试,确定该权值系数为:w4=100。

取适配函数为f=1/J。

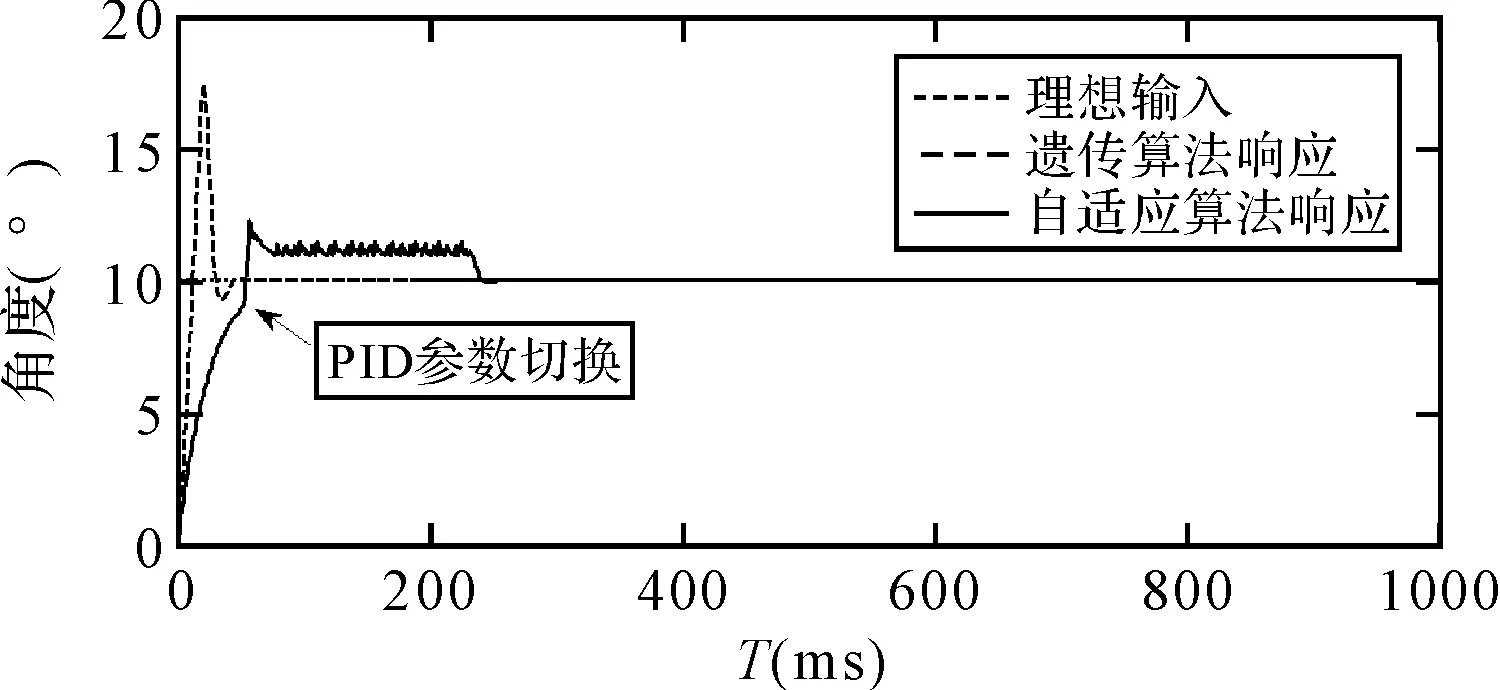
图6　基于遗传算法的外环控制回路单位阶上跃响应

如上图所示,当平台处于大偏角状态时,基于自适应算法的PID控制器与基于遗传算法的PID控制器相比,其优势在于: 1) 可以大大减小系统超调量; 2) 系统达到稳态之前的过渡过程时间较长。上述两点决定了基于自适应算法的控制器使系统控制过程相对平稳、冲击相对较小。由于PID参数的切换会引起控制回路的突变,所以在切换初期,系统会有小幅振荡,这个不会影响系统的稳态精度。

在正常工作情况下,平台始终处于小偏角状态,在这一状态下,基于遗传算法和基于自适应算法的控制器控制效果相同。因此,基于自适应算法的控制器既能使系统具有良好的控制特性,也能在平台大偏角启动或异常状态下对系统进行有效保护。

5结语

控制策略的选取直接影响重力测量稳定平台的整体性能。针对PID控制方法中存在的快速性和有效性的矛盾难以通过传统的参数整定方法得到有效解决的问题,本文研究了一种基于遗传算法的自适应PID控制方法。该方法一方面实现了PID参数的快速、有效寻优,最大程度上解决快速性和准确性之间的矛盾;另一方面,又兼顾了重力测量稳定平台的控制需求。从而能够实现对稳定平台的优化控制。仿真实验表明,该算法能够实现稳定平台的平稳启动、减小系统冲击,同时能够保证系统的稳态精度。最终作用于系统的PID参数可以保证系统有较强的鲁棒性。

参 考 文 献

[1] 吴章.CHZ海洋重力仪稳定平台的实验研究[D].武汉:华中科技大学,2009.

[2] 邵关.SII型海洋重力仪稳定平台颤动故障与排除方法[J].海洋测绘,2007,27(13):78-80.

[3] 杨秀丽.陀螺稳定平台结构分析及其优化设计[D].长春:中国科学院长春光学精密机械与物理研究所,2008.

[4] Astrom K J, Hagglund T, Hang C C, et al. Automatic tuning and adaptation for PID controllers-A survey[J]. Control Engineering Practice,1993(1):699-714.

[5] Hang C C, Ho W K, Cao L S. A comparison of two design methods for PID controllers[J]. ISATRANS,1994,33(2):147-151.

[6] 赵保才.基于遗传算法的鲁棒PID设计[D].天津:天津大学,2006.

[7] 徐磊.基于遗传算法的多目标优化问题的研究与应用[D].长沙:中南大学,2007.

[8] 丁寅磊.基于遗传算法的PID控制器参数优化研究[D].北京:华北电力大学,2008.

[9] 饶运清,严治雄,张超勇,等.一种混合遗传算法在车间作业调度中的应用研究[J].机械科学与技术,2006,25(5):584-587.

[10] Forrest S. Genetic algorithm principles of natural selection application to computation[J]. Science,1993,26(1):872-878.

中图分类号TP273

DOI:10.3969/j.issn.1672-9730.2016.03.012

作者简介:李昂,男,硕士,助理工程师,研究方向:惯性技术及应用。李楠,男,工程师,研究方向:惯性技术及应用。高远,男,研究方向:惯性技术及应用。郭斌,男,硕士研究生,研究方向:惯性技术及应用。

收稿日期:2015年9月3日,修回日期:2015年10月17日