介观二能级体系的量子输运特性研究
2016-04-14骆钧炎
胡 兢,骆钧炎
(浙江科技学院 理学院,杭州 310023)
介观二能级体系的量子输运特性研究
胡兢,骆钧炎
(浙江科技学院 理学院,杭州 310023)
摘要:利用电子数分辨的量子主方程,推导了介观输运体系中的电流和散粒噪声计算方法,研究了二能级体系的量子输运特性。在非对称隧穿耦合强度下,电流输运出现了快慢通道的输运机制,导致了动态库伦阻塞,以及新颖的负微分电导现象和超泊松散粒噪声。这些研究结果对量子器件的实现、优化和控制具有一定的实际意义。
关键词:量子点;介观体系;散粒噪声;输运特性
介观体系,就是介于微观和宏观之间的物理系统,因此介观物理是一个研究从经典物理向量子物理过渡的一个新的领域。由于介观尺度范围一般在纳米量级,因此,介观物理与纳米科学技术有着密不可分的关系。近年来,随着半导体超微细加工技术的不断进步,科学家可以像对原子、分子体系进行波函数相干操作那样在固体材料中“制备”出特定的量子态。这就意味着固体物理学研究已开始由“能带工程”进入到更深层次的涉及量子态相干调控的“波函数工程”阶段[1-4]。人们期望能够充分利用低维量子体系的相干性等微观物理特性,探索更普通化、更实用化的量子系统操控技术和方法。低维介观量子体系的研究不仅为科学家取得新的重大突破提出了新的机遇和挑战,也将有助于在固体领域内促进量子物理与信息科学的交叉与融合。
迄今为止,人们已经提出了不同的物理载体作为量子器件的基本单元。然而与大多数非固态量子器件相比,固态量子体系的最大优势在于它可以利用现有的纳米微加工技术来实现大规模集成化。这其中,量子点因为其制备与传统半导体加工工艺类似而具有优良的可控制和可扩展性,受到了人们的广泛关注[5-8]。对于量子点体系,包括其能级结构、量子隧穿强度、电子局域化及多体关联等在内的量子特性,都可以通过调节体系的尺寸、个体间的耦合强度及外场而得到精确控制。因此,如何有效地利用和调控这些量子特性,将量子点体系设计成具有特定功能的量子器件,就需要深入分析、理解并揭示其中的量子效应与物理机制。其研究无论从基础理论方面还是在促进固体量子物理与信息科学的交叉方面,都有重要的意义。
对于量子点体系,测量输运电流仍然是目前最常用和重要的研究方法之一。通过对电流的测量,可以得到很多与器件相关的输运特性。可是,任何测量过程都会受到噪声的影响。对于传统电子器件,人们希望尽可能地降低涨落噪声以达到较高的信噪比。然而在量子点器件中,由于电荷的分立特性,单位时间内通过导体的平均电量(即电流)不可避免地围绕其平均值附近涨落。正是载流子的量子化特性,使得量子涨落噪声不可能像传统器件的噪声那样可以被无限制地减弱。实际上,对于量子器件,其量子输运涨落并非一定有害,这些与时间相关的精细起伏,能够敏感地反映输运过程中具体的动力学行为,丰富的量子输运特性,以及器件内部精细的能量尺度等相当多的宝贵信息。因此,对量子涨落噪声的系统测试与分析,目前已经成为研究低维和介观纳米器件中载流子输运特性的一项重要理论工具和方法[9]。
在本文中,笔者将在电子数分辨的量子主方程基础上,推导得到针对介观输运体系中的电流和散粒噪声的计算方法。利用这一理论方法,深入地研究了二能级体系的量子输运特性。特别是,在非对称隧穿耦合强度下,电流输运出现了快通道和慢通道相互竞争的输运机制。这一机制导致了电荷输运过程中的动态库伦阻塞效应,以及新颖的负微分电导现象和超泊松散粒噪声。这些基本物理问题的研究,可能对二能级量子器件的实现、优化和控制具有一定的参考价值和实际意义。
1介观二能级输运体系
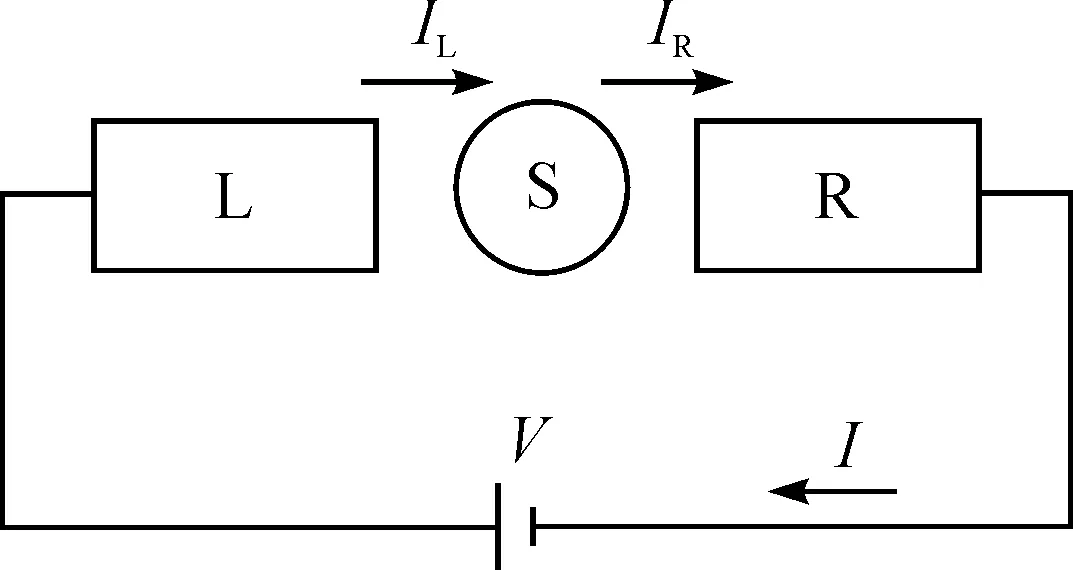
图1 电子在介观体系中的输运示意图Fig.1 Schematic setup for electron transport through mesoscopic system
介观二能级的输运由量子点和左右输运电极组成,如图1所示,其中S代表量子点体系,L和R分别代表左右电极。在左右电极上施加一偏压V,就会有电流流经量子点体系。左右电极的偏压决定了左右电极中电子的费米(Fermi)能量μL和μR。考虑由μL和μR窗口范围内量子点仅有两能级参与输运,那么整个体系的哈密顿量(Hamiltonian)就可以表示为
H=HS+HB+H′,
(1)
方程(1)中,HS为量子点两能级体系的哈密顿量。根据安德逊(Anderson)模型,HS可以表示为
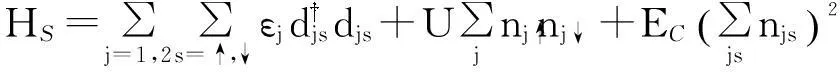
(2)
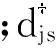
方程(1)中第二项HB表示左右电极,他们均被视为由自由电子组成,因此其哈密顿量可以表示为
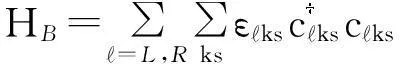
(3)
方程(1)中的最后一项表示二能级体系与左右电极之间的隧穿耦合,其哈密顿量可以表示为
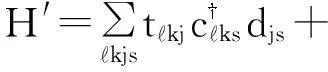
(4)
2量子主方程方法
2.1电子数分辨的量子主方程
对于如图1所示的介观量子输运体系,二能级体系是笔者所关心的。因此,从整个系统的密度矩阵ρT出发,对电极的自由度求迹(trace)即得到二能级体系的动力学特性,即ρ(t)=trB[ρT(t)],其中trB[(…)]表示对电极的自由度求迹。将系统与电极之间的耦合H′视为微扰并作二阶累积矩展开,即得到了描述二能级量子点体系密度矩阵ρ(t)的量子主方程[10]
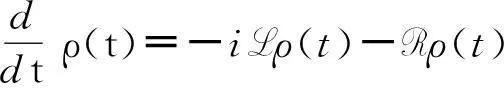
(5)
方程(5)中,第一项L(…)=[HS,(…)]为二能级体系的刘维(Liouvillian)超算子,而第二项则为二能级体系与电极之间的耦合引起的耗散
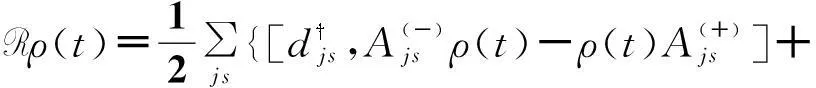
(6)
为了描述电子的输运特性,有必要将方程(5)拆解(unravel)为隧穿电子数“N”分辨的量子主方程[11-13]
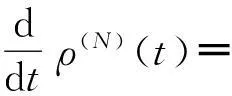
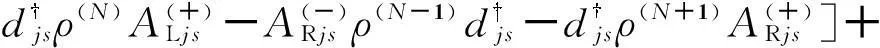
(7)
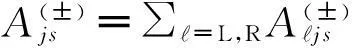
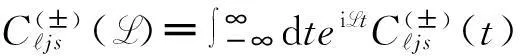
(8)
(9)
方程(9)中,〈…〉B=trB[(…)ρB],ρB为电子库的热平衡态,trB[…]为对电极中电子态的自由度求迹。
2.2隧穿电流
从电子数“N”分辨的量子主方程(7)可以得到很多介观体系的输运特性。例如,隧穿电子数的概率分布函数就可以表示为P(N,t)=tr[ρ(N)(t)],tr[…]表示对二能级体系的自由度求迹。根据隧穿电子数的概率分布函数,就可以得到隧穿的平均电流
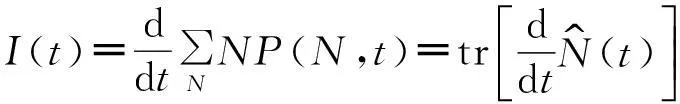
(10)
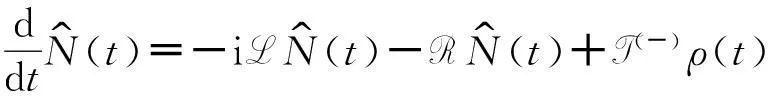
(11)
其中T(±)定义为

(12)
根据方程(10)可以得到输运电流为
I(t)=tr[T(-)ρ(t)],
(13)
方程(13)中,ρ(t)为量子主方程(5)的解。
2.3散粒噪声
单电子的隧穿过程本质上是随机过程,电流在平均值附近涨落,从而形成散粒噪声。隧穿电流散粒噪声可以通过Mac Donald公式[14]计算
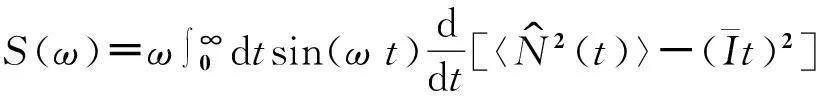
(14)
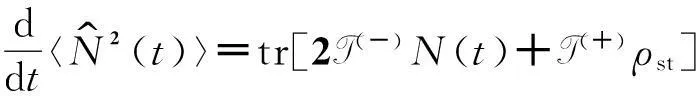
(15)
方程(15)中,ρst=ρ(t→∞)为量子主方程(5)的稳态解;N(t)可以通过方程(11)求解。
3二能级体系的输运特性
对于库伦阻塞的二能级体系,其占据态|χ,χ′〉(χ,χ′={0,σ,↑↓})、相应的本征能量和简并度如表1所示。其中,0代表该能级空占据,σ表示该能级被一个自旋向上(σ=↑)或自旋向下(σ=↓)的电子占据,↑↓代表该能级同时被自旋向上和自旋向下的电子占据。图2给出了二能级输运体系的电流-电压曲线,其中取了对称隧穿强度,即Γj=Γ。可见,随着电压的升高,电流出现明显的台阶现象,电压越高,台阶也越高。这是因为电压越高,电子能够参与输运的能级通道越多,因此电流越大。所以,电流的每级台阶与表1中的每个本征能量有着密切的联系。
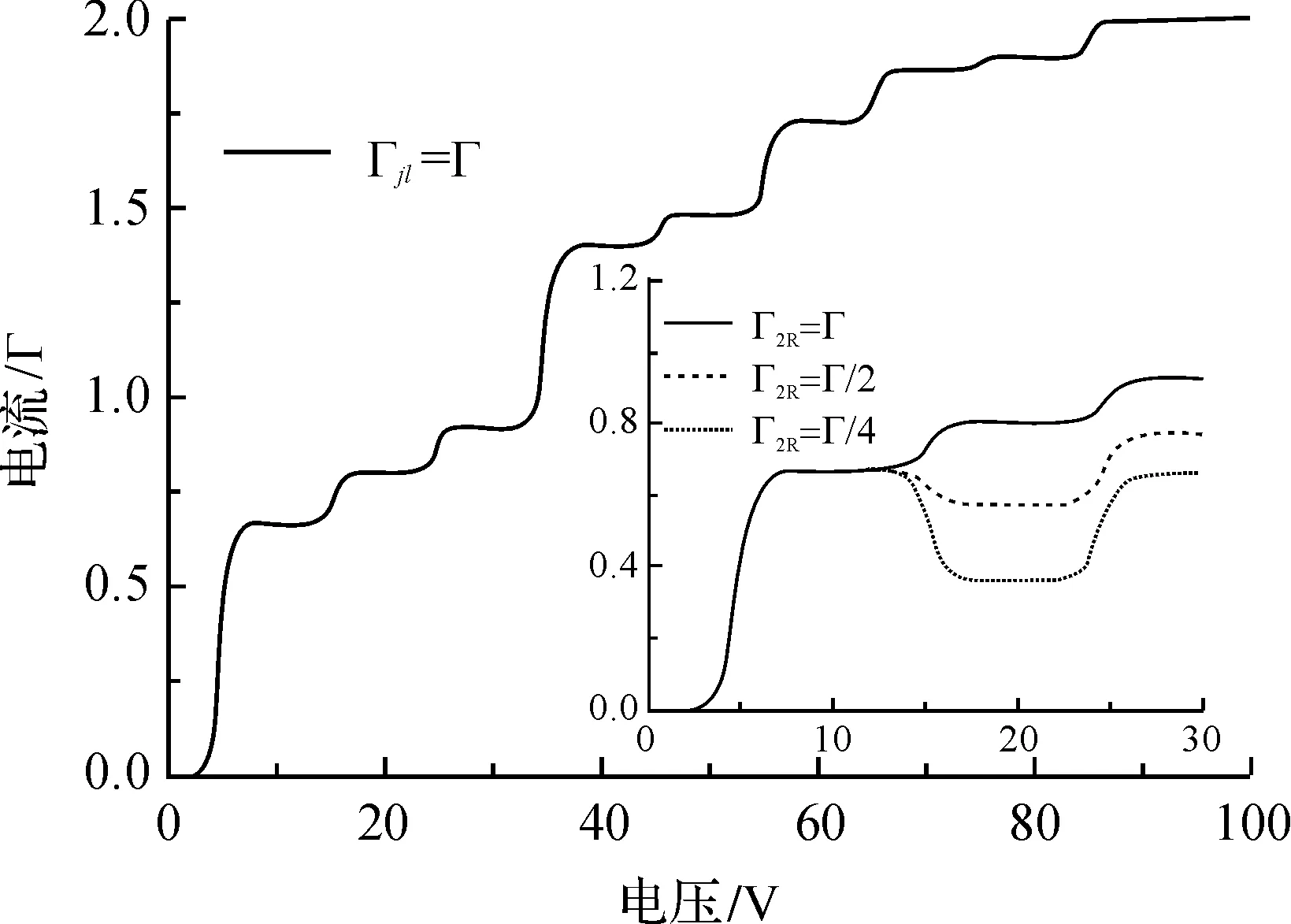
图2 二能级体系的电流电压特性曲线(插图是不同Γ2R情形下的电流)Fig.2 Current-voltage characteristics of two-level system(Inset: current for various Γ2R)

占据态能量简并度|0,>01|σ,0>ε1+EC2|0,σ>ε2+EC2|σ,σ'>ε1+ε2+4EC4|↑↓,0>2ε1+U+4EC1|0,↑↓>2ε2+U+4EC1|↑↓,σ>2ε1+ε2+U+9EC2|σ,↑↓>ε1+2ε2+U+9EC2|↑↓,↑↓>2ε1+2ε2+2U+16EC1
为了研究非对称耦合情况下的电流电压特性,图2中的插图给出了不同Γ2R情形下的输运电流。随着电压的升高,电流能不能上一个台阶依赖于Γ2R的大小。由图明显地可以看到,当Γ2R较小时(如Γ2R=Γ/4),随着电压的升高,电流反而下了一个台阶。电流随电压的升高而降低就意味着其微分电导为负值(negative differential conductance,NDC)。为了研究产生负微分电导的原因,现采用量子主方程方法具体分析电流第一和第二个台阶的情况。
3.1第一电流台阶的输运特性
电流第一个台阶对应的偏压范围为μL>ε1+EC>μR,即只有单能级ε1+EC处于左右偏压范围内,对应的占据态是|0,0和|σ,0(σ=↑,↓),因此电荷输运只有一个通道。在这种情况下,量子输运的主方程可以简单地表示为ρ(t)=M1ρ(t),其中

(16)
这里,Γ1L和Γ1R分别为单能级与左右电极的隧穿耦合强度。根据方程(5)和(13),得到第一个台阶对应的电流值为
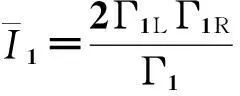
(17)
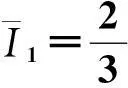
第一个台阶电流对应的零频噪声可以根据方程(14)和(15)计算得到:
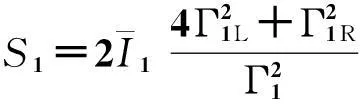
(18)
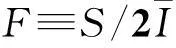
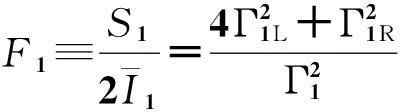
(19)
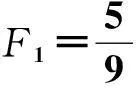
3.2第二电流台阶的输运特性
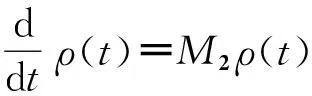

(20)
这里,Γ2L和Γ2R分别为能级ε2+EC与左右电极的隧穿耦合强度。根据方程(5)和(13),不难得到第二个台阶对应的电流值
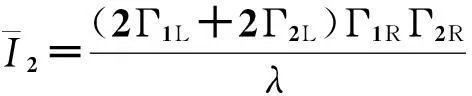
(21)
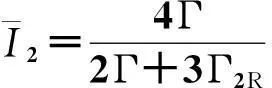
为了进一步解释负微分电导现象,利用方程(14)和(15)计算得到了该区域的零频法诺因子
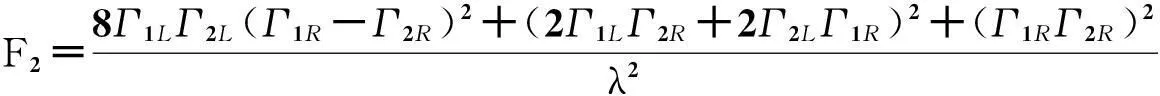
(22)
该结果与文献[16]中通过实时费曼图展开方法得到的结论一致。这里仍然考虑Γ1L=Γ1R=Γ2L=Γ的情形,随着Γ2R的减少,发现第二个电流平台对应的法诺因子会随之增加。在Γ2R→0极限下,该台阶对应的法诺因子F1→3.0>1.0,即出现了一般来讲只有玻色子会出现的超泊松噪声,而产生这一行为的原因在于电流输运中出现的动力学库伦阻塞[16-17]。电子可以通过两通道ε2+EC和ε1+EC输运。当Γ2R较小时,电流在ε2+EC通道的输运较慢,而在ε1+EC通道的输运相对较快。由于二能级体系存在较强的库伦相互作用能U和充电能EC,因此在同一时刻二能级体系最多只能占据一个电子。当电子占据慢通道时,电荷输运被堵塞,当电子从慢通道隧穿出去后,快通道就可能打开,随之而来的是一连串电子通过二能级体系,直到下一时刻二能级体系再次占据慢通道。这一过程即被称之为动力学库伦阻塞,而形成这一机制的原因正是快通道和慢通道的相互竞争机制[18-20]。
为了进一步分析电流的噪声特性,通过方程(14)和(15)计算,并首次得到了双通道情况下的含频散粒噪声谱的解析结果:
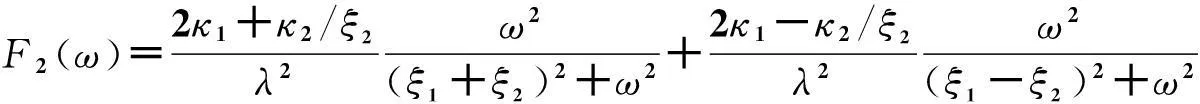
(23)
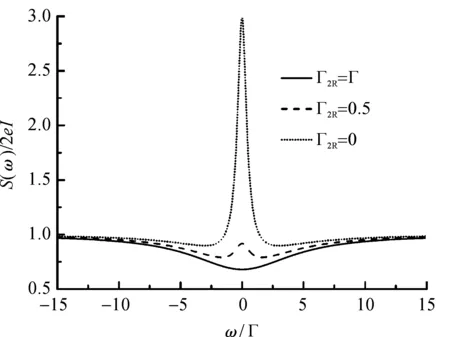
图3 介观二能级体系中量子输运的含频散粒噪声特性 Fig.3 Frequency-dependent shot noise for quantum transport through two-level system
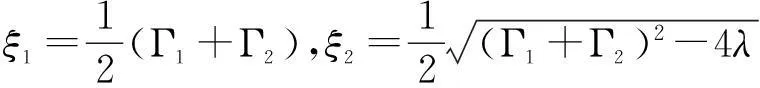
1)考虑Γj=Γ,含频散粒噪声谱简化为
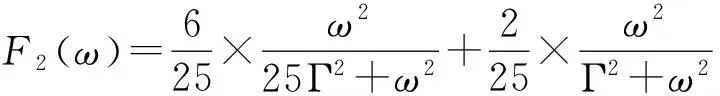
(24)
可见,它由两个洛伦兹谱组成,展宽分别为5Γ和Γ。但是,由于展宽为5Γ的洛伦兹谱权重较大,因此含频散粒噪声由该部分占主导,此时ω=0处是噪声谱的最小值。这也表明,在没有快慢通道的相互竞争区域,电流噪声表现为亚泊松特性,显著特征就是噪声谱的最小值出现在ω=0区域,如图3实线所示。
2)当Γ1L=Γ1R=Γ2L=Γ且Γ2R→0极限下,含频散粒噪声谱化简为
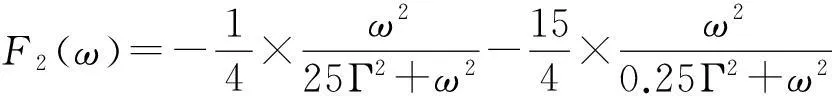
(25)
此时,噪声特性仍由两个洛伦兹谱组成,展宽分别为5Γ和0.5Γ,但是展宽为0.5Γ的洛伦兹谱权重较大,现在ω=0处是噪声谱的最大值。在此参数条件下,电荷输运出现快慢通道相互竞争的机制,而其特征就是噪声最大值出现在ω=0,可参照图3中的点线。
3)当Γ1L=Γ1R=Γ2L=Γ且Γ2R介于零和Γ之间时(如Γ2R=0.5Γ),两个洛伦兹谱组旗鼓相当,均不占优势。因此,噪声谱表现为两个不同带宽的洛伦兹谱的叠加,如图3中虚线所示。
通过以上分析表明,电流的噪声特性,尤其是频率相关的噪声能够深入地揭示电荷输运的动力学过程。通过对噪声特性的分析,能够探究电荷输运过程中快慢通道竞争的机制。因此,除了测量电流之外,噪声谱也是研究不同参数条件下输运特性的一种非常重要的方法,从而为固态量子器件的设计和制造提供了参考。
4结语
在电子数分辨的量子主方程方法的基础上,推导得到了计算介观体系中量子输运特性的理论方法,并在此基础上研究了二能级体系的输运电流和散粒噪声特性。在二能级与电极隧穿耦合强度非对称的条件下,发现了单电子输运过程中出现了快通道和慢通道相互竞争的机制,由此导致了动态库伦阻塞效应,以及新颖的负微分电导现象和超泊松散粒噪声。通过含频噪声的分析,进一步解释了输运器件内部一些细微的动力学行为,因而对二能级量子器件的优化和控制具有一定的指导意义。
参考文献:
[1]MICHLERP.Singlequantumdots:fundamentals,applications,andnewconcepts[M].Berlin:Springer-Verlag, 2003.
[2]MAKHLINY,SCHÖNG,SHNIRMANA.Quantum-stateengineeringwithJosephson-junctiondevices[J].ReviewofModernPhysics, 2001, 73(2): 357.
[3]MOSSHAMMERK,BRANDEST.Semiclassicalspin-spindynamicsandfeedbackcontrolintransportthroughaquantumdot[J/OL].PhysicalReviewB, 2014, 90(13):134305 [2015-10-15].http://journals.aps.org/prb/abstract/10.1103/PhysRevB.90.134305.
[4]VIJAYR,MACKLINC,SLICHTERDH,etal.Quantumfeedbackcontrolofasuperconductingqubit:persistentRabioscillations[J].Nature, 2012, 490(6): 77.
[5]孙昌璞.量子测量问题的研究及应用[J].物理,2000,29(8):457.
[6]陈东敏,赵宏武,梁学锦,等.发展固态量子信息与计算的实验研究[J].物理,2008,37(6):433.
[7]ZHANGH,GUOGP,TUT,etal.QuantumcomputationandBell-statemeasurementswithdouble-dotmolecules[J/OL].PhysicalReviewA, 2007, 76(1): 012335 [2015-10-13].http://journals.aps.org/pra/abstract/10.1103/PhysRevA.76.012335.
[8]GUOGP,ZHANGH,HUY,etal.Dispersivecouplingbetweenthesuperconductingtransmissionlineresonatorandthedoublequantumdots[J/OL].PhysicalReviewA, 2008, 78(2): 020302[2015-10-14].http://journals.aps.org/pra/abstract/10.1103/PhysRevA.78.020302.
[9]BLANTERYM,BüTTIKER M. Shot noise in mesoscopic conductors[J]. Physics Reports, 2000, 336(1): 1.
[10]YAN Y J. Quantum Fokker-Planck theory in a non-Gaussian-Markovian medium[J/OL]. Physical Review A, 1998, 58(4): 2724 [2015-10-15]. http://journals.aps.org/pra/abstract/10.1103/PhysRevA.58.2721.
[11]LI X Q, LUO J Y, YANG Y G, et al. Quantum master-equation approach to quantum transport through mesoscopic systems[J/OL]. Physical Review B, 2005, 71(20): 205304-3 [2015-10-22]. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.71.205304.
[12]LUO J Y, LI X Q, YAN Y J. Calculation of the current noise spectrum in mesoscopic transport: a quantum master equation Approach[J/OL]. Physical Review B, 2007, 76(8): 085325-2 [2015-10-25]. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.76.085325.
[13]LUO J Y, JIAO J H, XIONG B T, et al. Non-Markovian dynamics and noise characteristics in continuous measurement of a solid-state charge qubit[J/OL]. Journal Applied Physics, 2013, 114(17): 173703-5 [2015-10-26]. http://scitation.aip.org/content/aip/journal/jap/114/17/10.1063/1.4828870.
[14]MACDONALD D K C. Noise and fluctuations: an introduction [M]. New York: Wiley, 1962.
[15]CHEN L Y, TING C S. Theoretical investigation of noise characteristics of double-barrier resonant-tunneling systems[J/OL]. Physical Review B, 1991, 43(5): 4535[2015-10-28]. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.43.4534.
[16]THIELMANN A, HETTLER M H, KÖNIG J, et al. Super-Poissonian noise, negative differential conductance, and relaxation effects in transport through molecules, quantum dots, and nanotubes[J/OL]. Physical Review B, 2005, 71(4): 045341-6 [2015-10-29]. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.71.045341.
[17]COTTET A, BELZIG W, BRUDER C. Positive cross correlations in a three-terminal quantum dot with ferromagnetic contacts[J/OL]. Physical Review Letters, 2005, 92(20): 206801-1 [2015-11-01]. http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.92.206801.
[18]LUO J Y, JIAO J H, XIONG B T, et al. Spin-resolved bunching and noise characteristics in double quantum dots coupled to ferromagnetic electrodes[J/OL].Journal Physics: Condensed Matter,2013, 25(13): 155304-1 [2015-10-23]. http://iopscience.iop.org/article/10.1088/0953-8984/25/15/155304/meta;jsessionid=969B0A72CC1042CF 46EAEF7508A9D6CD.c1.iopscience.cld.iop.org.
[19]LUO J Y, HU J, LANG X L, et al. Conditional spin counting statistics as a probe of Coulomb interaction and spinresolved bunching[J]. Physical Letters A,2014, 378(11): 897.
[20]LUO J Y, JIAO H J, HU J, et al. Qubit detection with a T-shaped double quantum dot detector[J/OL]. Physical Review B, 2015, 92(4): 045107-1 [2015-07-07]. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.92.045107.
Quantum transport characteristics in mesoscopic two-level system
HU Jing, LUO Junyan
(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)
Abstract:Based on the electron-number-resolved quantum master equation, an approach to the calculation of current and shot noise in mesoscopic system is derived, which allows us to study transport properties in a quantum two-level system. Under the condition of asymmetric tunnel-couplings, a fast-to-slow mechanism is developed in electron transport, which leads to a dynamic Coulomb blockade, negative differential conductance, as well as super-Poisonian shot noise. It may be of great significance in the realization, optimization and control of quantum devices.
Keywords:quantum dot; mesoscopic system; shot noise; transport characteristics
中图分类号:O469
文献标志码:A
文章编号:1671-8798(2016)01-0024-08
通信作者:骆钧炎,男,副教授,博士,主要从事固态量子信息及相关物理问题的研究。
作者简介:胡兢(1981—),女,浙江省湖州人,工程师,硕士,主要从事量子输运研究。
基金项目:国家自然科学基金项目(11204272);浙江省自然科学基金项目(LY15A040007)
收稿日期:2015-11-18
doi:10.3969/j.issn.1671-8798.2016.01.005
浙江科技学院学报,第28卷第1期,2016年2月
Journal of Zhejiang University of Science and Technology
Vol.28 No.1, Feb. 2016
