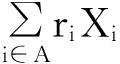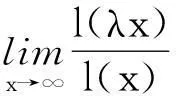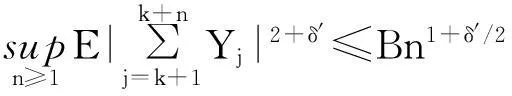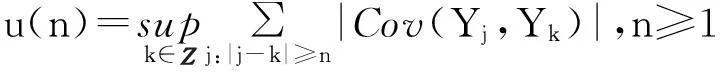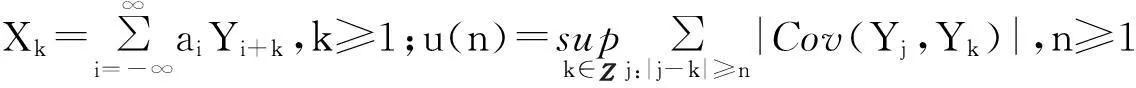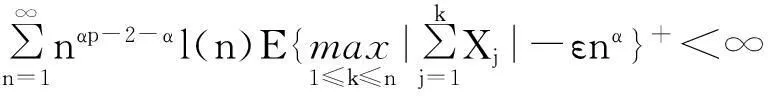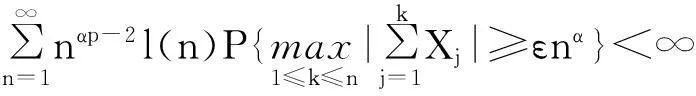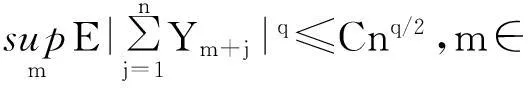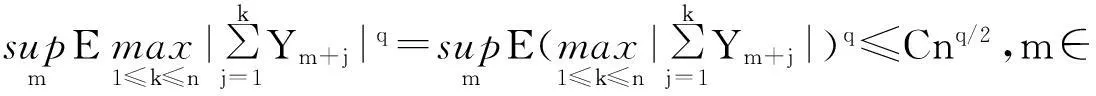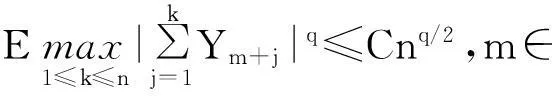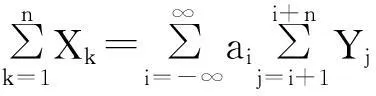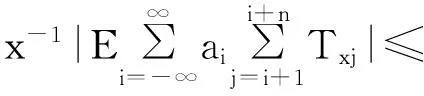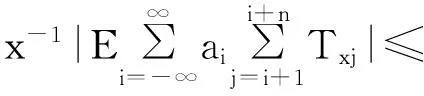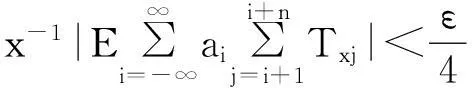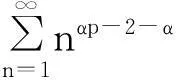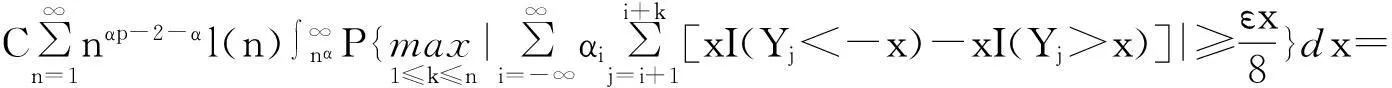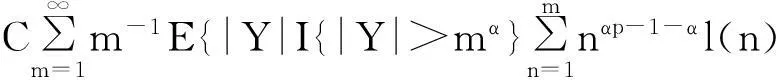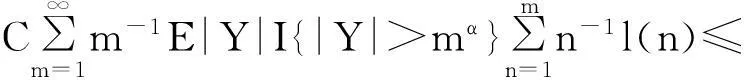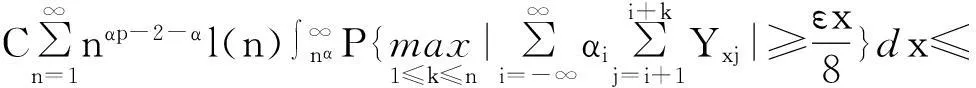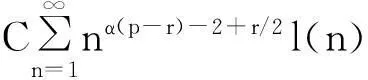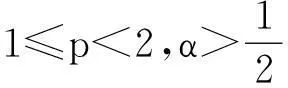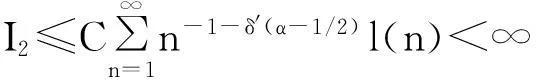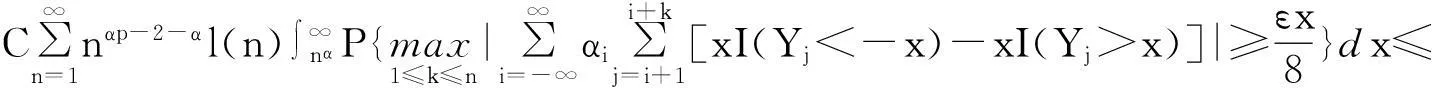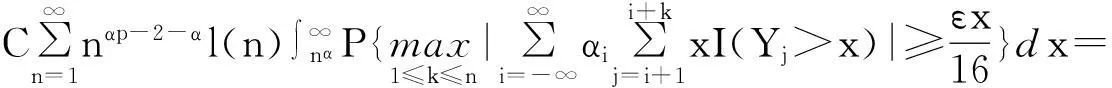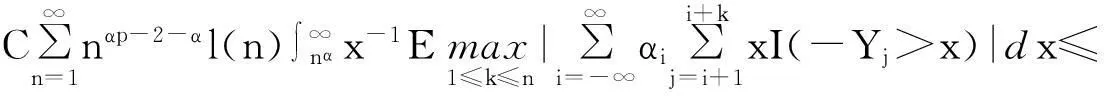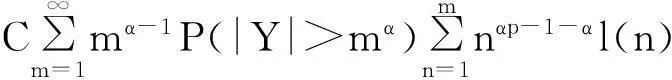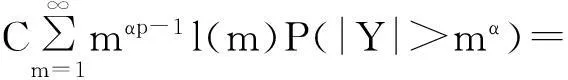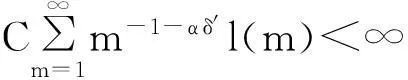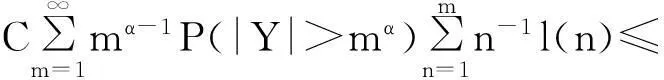LPQD序列生成的移动平均过程的矩完全收敛性

沈建伟

(浙江科技学院 理学院, 杭州 310023)



LPQD序列生成的移动平均过程的矩完全收敛性

沈建伟

(浙江科技学院 理学院, 杭州 310023)

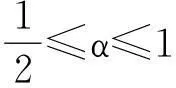
摘要:令{Yi,-∞

关键词:移动平均过程；矩完全收敛性；LPQD序列

1引理

定义1[1]1137，[2]130称随机变量X和Y是PQD (positively quadrant dependent)的，若对∀x,y∈都有

P(X≤x,Y≤y)≥P(X≤x)P(Y≤y)，

当前对于LPQD序列的研究已取得了不少成果。文献[2-3]分别获得了强平稳LPQD过程的中心极限定理和泛函中心极限定理,文献[4]得到了LPQD序列的不变原理,文献[5]建立了平稳LPQD序列生成线性过程的中心极限定理,文献[6]获得了平稳LPQD列生成线性过程部分和的精确渐近性,文献[7]建立了非平稳的LPQD序列和LNQD序列生成线性过程部分和的矩不等式。

本研究得到了不同分布的LPQD序列生成的线性过程的部分和的最大值的矩完全收敛结果。为行文方便,总是假定C代表正常数,并在不同的地方可以代表不同的值。以下是一些定义和相关的引理。

定义3[9]设C是一个正常数,{Yi,-∞

引理1[4]489令{Yi,i≥1}是一个LPQD随机变量列,EYi=0,存在δ>0,E|Yi|2+δ<∞。假定对0<δ′<δ,u(n)=O(n-δ′(2+δ)/2(δ-δ′));那么存在常数B>0使得对∀k∈,有

引理2[1]1138设随机变量X和Y是PQD的，则

1)EXY≥EXEY;

2)若f、g同为非降(或非增)函数，则f(X)与g(Y)仍为PQD的。

引理3[10]设{Xn,n≥1}是任意随机序列。如果存在某随机变量X,使对任意x>0及n≥1,有P(|Xn|≥x)≤CP(|X|≥x),则对∀β>0,∀t>0有

E|Xn|βI(|Xn|≤t)≤C(E|X|βI(|X|≤t)+tβP(|X|>t)),

E|Xn|βI(|Xn|>t)≤CE|X|βI(|X|>t)。

引理4[11]设l(x)是在无穷远处的慢变函数,则

2主要结果

(1)

注：1)令a0=1；ai=0,i≠0，则Xk=Yk,且{ai,-∞

2)若{Yi,-∞0,使得E|Y1|2+δ<∞,且E|Y1|p+δh(|Y1|1/α)<∞,则定理1的结论仍成立。

3)因LPQD序列蕴含了PA序列，故定理1的结果也适合于PA序列。

4)由于矩完全收敛性蕴含了完全收敛性,故在定理1的条件下，式(1)蕴含了

证明由引理1可得,对∀2

(2)

由Stout[12]的定理3.7.5及式(2)可得

于是

(3)

记

Txj=-xI(Yj<-x)+YjI(|Yj|≤x)+xI(Yj>x),Yxj=Txj-ETxj。

由引理2可知,{Yxj,-∞

当x>nα时,

1)若α>1,由引理3可得

Cx-1n[E|Y|I|Y|≤x}+xP(|Y|>x)]≤

Cn1-α→0,n→∞。

Cx-1nE|Y|I{|Y|>x}≤

Cx1/α-1E|Y|I{|Y|>x}≤

CE|Y|1/αI{|Y|>x}≤

CE|Y|pI{|Y|>x}→0,n→∞。

从而

现证明I1<∞。由Markov不等式和引理3知

1)如果p>1,则αp-1-α=α(p-1)-1>-1,由引理4知

CE|Y|pl(|Y|1/α)<∞。

2)如果p=1,对于∀δ>0,由引理4知

CE|Y|1+δl(|Y|1/α)<∞。

由上述讨论可知I1<∞。

再证明I2<∞。由Markov不等式、Hölder不等式及式(3)知

其中,取2

最后证明I3<∞。

1)如果p>1,则αp-1-α=α(p-1)-1>-1,由引理4知

2)如果p=1,对于∀δ>0,由引理4知

CE|Y|1+δl(|Y|1/α)<∞。

对于I32,证明类似于I31,不赘述，于是I32<∞。

综上所述,I1<∞,I2<∞,I3<∞。

证毕。

参考文献:

[1]LEHMANN E L. Some concepts of dependence[J].The Annals of Mathematical Statistics,1966,37(5):1137.

[2]NEWMAN C M. Asymptotic independence and limit theorems for positively and negatively dependent random variables[J]. Inequalities in Statistics and Probability (IMS Lecture Notes-Monograph Series),1984,5:127.

[3]BIRKEL T.A functional central limit theorem for positively dependent random variables[J]. Journal of Multivariate Analysis, 1993,44(2):314.

[4]林正炎.正相依随机变量的不变原理[J].数学年刊,1996,17A(4):487.

[5]KIM T S, BAEK J I. A central limit theorem for stationary linear processes generated by linearly positively quadrant-dependent process[J]. Statistics and Probability Letters, 2001,51: 299.

[6]谭希丽,杨晓云.LPQD列生成线性过程部分和的精确渐近性[J].吉林大学学报(理学版),2009,47(2):251.

[7]沈建伟.非平稳相依序列生成线性过程部分和的矩不等式[J].兰州理工大学学报,2012,38(3):150.

[8]杨启帆.关于正则变化函数与慢变函数[J].浙江大学学报(自然科学版),1990,24(2):318.

[9]GUO M L, DAI J J, ZHU D J. Complete moment convergence of moving average processes under negative association assumptions[J].应用数学,2012,25(1):119.

[10]吴群英.混合序列的概率极限理论[M].北京:科学出版社,2006:173.

[11]ZHOU X C. Complete convergence of moving average processes under φ-mixing assumptions[J].Statistics and Probability Letters,2010,80(5/6):287.

[12]STOUT W F. Almost sure convergence[M].New York: Academic Press, 1974:198.

Complete moment convergence for moving average process generated by LPQD sequences

SHEN Jianwei

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract:Let {Yspan,-∞

Keywords:moving average process; complete moment convergence; LPQD sequences

中图分类号:O211.4

文献标志码:A

文章编号:1671-8798(2016)01-0007-05

作者简介:沈建伟(1972—),男,浙江省萧山人,讲师,硕士,主要从事概率极限理论研究。

收稿日期:2015-11-01

doi:10.3969/j.issn.1671-8798.2016.01.002

浙江科技学院学报,第28卷第1期,2016年2月

Journal of Zhejiang University of Science and Technology

Vol.28 No.1, Feb. 2016