Underwater bearing-only tracking based on square-root unscented Kalman filter smoothing algorithm

WANG Bao-bao, WU Pan-long

(1. 716th Research Institute, China Shipbuilding Industry Corporation, Lianyungang 222006, China; 2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

Underwater bearing-only tracking based on square-root unscented Kalman filter smoothing algorithm

WANG Bao-bao1, WU Pan-long2

(1. 716th Research Institute, China Shipbuilding Industry Corporation, Lianyungang 222006, China; 2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)

In passive tracking, the nonlinearity may cause computational complication and precision degradation. To solve this problem, a novel filtering-smoothing algorithm based on Square-Root Unscented Kalman Filter (SR-UKFS) is proposed to track underwater target. In the SR-UKFS algorithm, the Square-Root Unscented Kalman Filter (SR-UKF) is used as forward-filtering algorithm to provide current location results, and the Rauch-Tung-Striebel (RTS) algorithm smoothes the previous state vector and covariance matrix using the current location results. Therefore an initial value with higher precision is obtained to get more precisely locating results. Comparative analysis and validation are made on the tracking performances of SR-UKFS algorithm and SR-UKF algorithm, and the experiment results show that, under the same conditions, the SR-UKFS can more effectively improve the tracking precision than the SR-UKF algorithm. The SR-UKFS algorithm can reduce nearly 59% of the position error and nearly 54% of the velocity error. The SR-UKFS is an effective underwater bearing-only target tracking algorithm, and can provide valuable references for designing the underwater bearing-only target tracking system.

target tracking; bearing-only; square-root unscented Kalman filter; smoothing algorithm; forward-filtering; backward- smoothing

Using single observer to track targets avoids complex time synchronization. It provides significant practical value with strong independence and good motility. When relative movements exist between the observer and target and so does observability, the observer can track targets[1]. Underwater target motion analysis is a technique for estimation of target motion parameters, which is based on a series of measured data sequence (including azimuth angle and pitch angle) from hydrophone array of sonar platform[2]. The core of thistechnique is filtering algorithm, which is utilized to locate and track. Because of severe system nonlinearity, underwater target tracking shall face the linearization problems of state equation and measurement equation. Regarding the nonlinearity of state equation or measurement equation, related literatures adopt many modified Kalman filtering algorithms, like Extend Kalman Filter (EKF), UKF, SR-UKF and so on[3].

EKF property depends on partial nonlinear strength. During the linearization process of EKF, Jacobian matrix is required, which sometimes makes difficulty in realization[4-5]. UKF approximates to-be-estimated parameters by constructing a group of certain weighted sample points, which avoids the linearization modeling of nonlinear objects and calculation of Jacobian matrix as a filtering algorithm which can be directly utilized in nonlinearity system for mode estimation[6]. But in practical utilization, the data round-off error may make covariance matrix negative definite, which fails the UKF algorithm in calculating the matrix square root. Compared with EKF and without additional calculated amount, UKF makes it that estimated accuracy and rate of convergence are apparently enhanced. SR-UKF algorithm estimates squarerooting matrix of error to do the recursive calculation, which solves the problem of negative definite covariance matrix and filtering divergence due to calculation error and noise signal in standard UKF algorithm, and enhances the accuracy and stability of filtering[7].

RTS smoothing algorithm is a fixed interval optimal smoothing technique, it greatly simplifies the process of calculation, and is often used to smooth the data from the filtering operation[8]. Smoothing can build a coherent connection at series of estimations, which makes the estimations more resistant to disturbance[9].

Based on SR-UKF, SR-UKFS adds backward smoothing for better accuracy of target state estimation in last moment, and enhances target state estimation accuracy of this moment[10]. Compared with the SR-UKF algorithm, the SR-UKFS algorithm requires a longer operation period. However, with the application of high-performance processors or the realization of filter algorithm based on FPGA, SR-UKFS algorithm can meet real-time requirements[4]. According to the relative location of target and observation platform, the paper is based on the information of noise measurement of azimuth angle and pitch angle from passive sonar, tracks the course of underwater target with the utilization of SR-UKFS, and makes the simulation comparisons between standard UKF algorithm and SR-UKF algorithm.

1 Tracking principle and system model

The basic function of passive sonar is to find direction to measure azimuth information (including azimuth angle and angular altitude) formed by wave beam. Azimuth angle includes the location information of target horizontal direction. Angular altitude includes the information of target depth. Among the research about orientation and tracking problem of underwater target, the shape and size of observer and target can be ignored as particle of space, and the acceleration of target can be seen as a result of noise excitation and a Gaussian random process[11]. The relations of relative movement between target and observing platform can be seen in Fig.1.

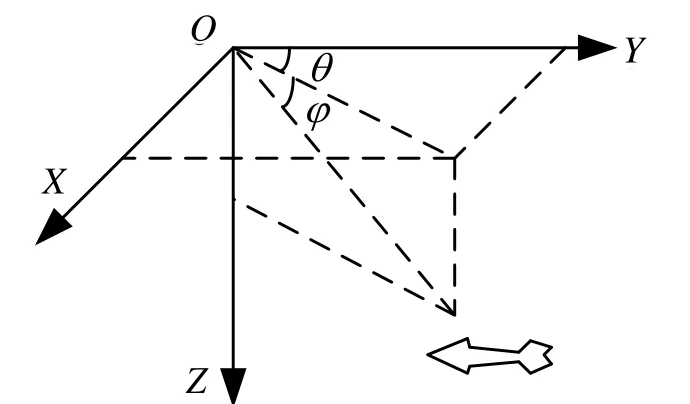
Fig.1 Location relationship between target and observation platform

In passive sonar tracking system, the information of sonar measurement can be obtained from a spherical coordinate[12]. Target dynamic model is usually constructed in rectangular coordinate system. Thus, the target tracking of sonar becomes a nonlinear estimation problem. The main methods to solve this problem are EKF, UKF and SR-UKF. This paper adopts SR-UKFS algorithm to track the target, namely, firstly uses SR-UKF algorithm to estimate target state, and then uses RTS smoothing algorithm to obtain the target state estimation of last moment, and finally adopts SR-UKF algorithm to estimate the target state of this moment.

In rectangular coordinate, a linear dynamic model and a nonlinear observing model can be used to establish a target motion model. The state variable is

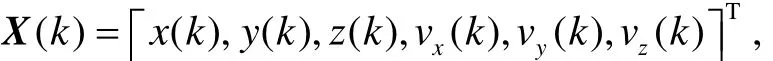
and x,y,z means the relative location of X, Y, Z directions;vx, vy, vzmeans the relative speed of X, Y, Z directions. The discrete state equation of system is

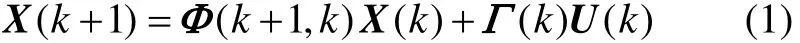
where

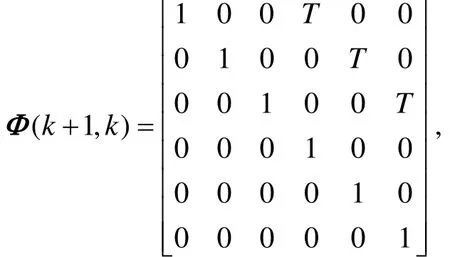
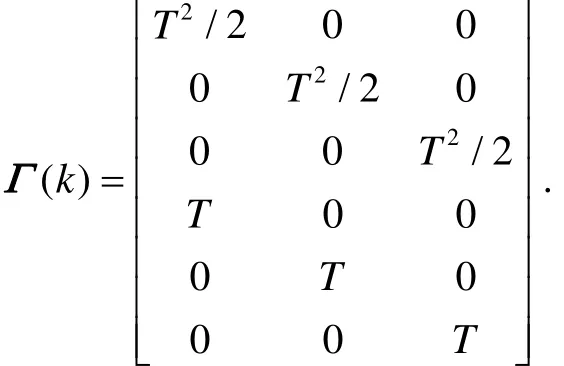
xyz T is the sampling period of system.

The observed quantity of system includes azimuth angle θ(k) and pitch angle φ(k), which can be seen in Fig.1. In rectangular coordinate system, the formula of azimuth angle and pitch angle can be seen in Formula (2):

When the target depth z(k) is a fixed value, the observed quantity of azimuth angle and pitch angle can be transferred to the position quantity of target in direction X and Y, and the transition measurement equation of system can be seen in Formula (3):

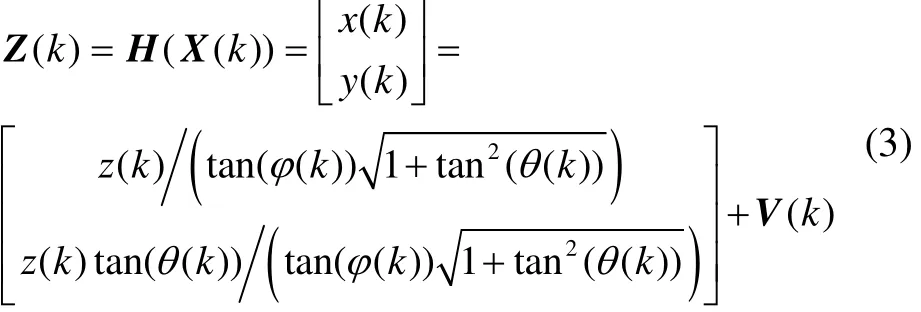
The measuring error of azimuth angle and pitch angle is relatively independent zero-mean Gaussian white noisis the measurement noise caused by azimuth angle and pitch angle, its variance matrix is R, and

2 SR-UKFS algorithm

UKF is proposed by Julier, and widely used in the field of nonlinear estimation. But in practice, due to the round-off error in numerical calculation, sometimes we may get negative definite covariance matrix, which leads to the stoppage of UKF filter[13]. In order to avoid failure, SR-UKF uses covariance square root to replace the covariance to take part in recursive calculation, which ensures the half positive definitiveness of covariance in basic state has better numerical characteristics[14].

In the process of UKF filtering, the calculation of new Sigma point in every update requires a considerable number of calculation. Everytime we must calculate the square root of state covariance matrix P, and assumesT= SS P. In the process of SR-UKF filtering,S will be recorded to avoid heavy decomposition calculation in every resampling, which enhances the operation speed of UKF. QR disintegration and Cholesky disintegration update are two important concepts in SR-UKF.

QR disintegration: for matrixfinding an orthogonal matrixand an upper triangular matrixto make AT=QR, which is doing a QR disintegration for matrix A. qr{·} can be used as QR disintegration with R as returned value. According to the analysis knowledge of matrix,that is Ris also the transposition of Cholesky coefficient S in matrix

Cholesky disintegration update: if S is the Cholesky disintegration of matrix, andso the Cholesky disintegration update of matrixcan be marked asu usually is a column of vectors, but if u is a matrix which includes factors in M column, and uses vectors in M column to M times first order Cholesky update successively. In filtering process, S displaces P to participate in recursive calculation which can ensure the nonnegative definitiveness of covariance matrix for effective filtering.

For both UKF algorithm and SR-UKF algorithm, target state estimation of this moment is related to both current measured value and the state estimation of last moment. Thus, the state estimation accuracy enhancement of last moment can enhance the tracking accuracy. SR-UKFS uses RTS algorithm as the forward filter algorithm to backward smooth the received target state estimation, to obtain a precise target state estimation of last moment, and uses SR-UKF for secondary filtering. Fig. 2 shows the process of SR-UKFS algorithm.

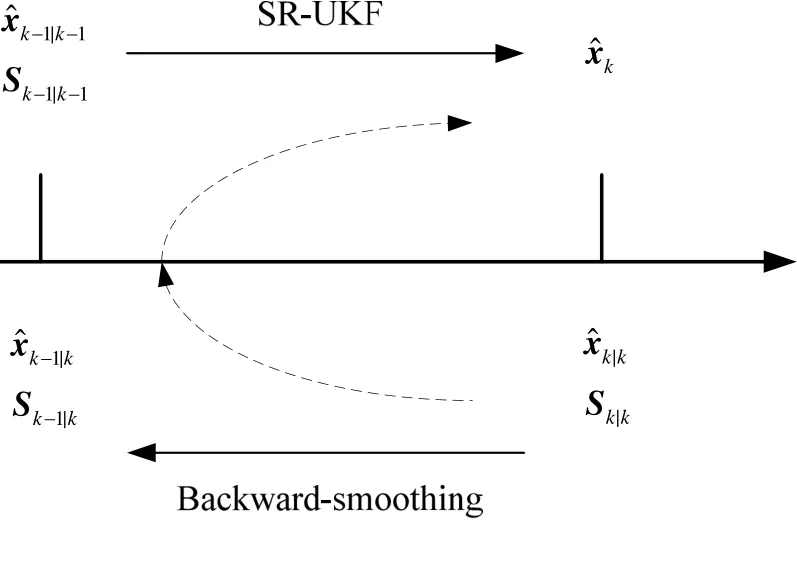
Fig.2 The process of SR-UKFS

The calculation step of SR-UKFS is given as:

Step 1: Parameters initialize

Step 2: Selection of sigma points

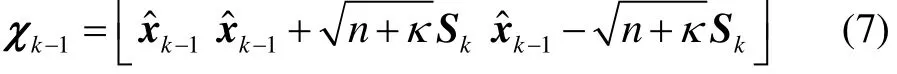
Step 3: Time update equations

Step 4: Measurement update equations

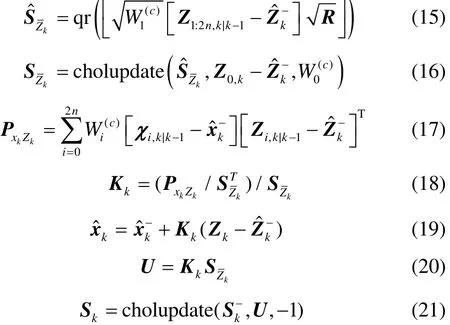
Step 5: Smoothing process

Step 6: Second forward SR-UKF filtering

Replacing xˆk-1,Sk-1byxˆk-1|k,Sk-1|k, and repeating step 2 to step 4.

where

3 Simulation results and analysis

During the observation, sonar observation platform is motionless. The sonar observation platform is considered as coordinate reference point, underwater target aircraft straightly motions at a constant speed 500 meters away from observation platform in a stable state, and the speed is 8m/s. The initial azimuth angle is 300 with respect to observation platform, the depth is 45 m. The relations of relative location constitute the threedimensional situation with known depth. And z= 45 m,, the target state vector can be simplified asThe simulation condition and related parameters: sampling period T=0.1 s, noise variance matrix of systemthe measured noise standard deviation of azimuth angle and pitch angle in passive sonarThe initial state vector of targthe covariance matrix of original state errothe simulation time is 46 s. The filtering parameter ofUnder above-mentioned conditions, the author evaluates the performances of UKF, SR-UKF and SR-UKFS, which are used for underwater pure orientation targets. Fig.3 and Fig.4 are the estimation variance of location of x and y direction, Fig.5 and Fig.6 are estimation variance of speed of x and y direction. Tab.1 is the comparison of location and speed mean square after the filters of UKF, SR-UKF and SR-UKFS. The simulation results clearly show that UKF has the worst tracking accuracy, the stability of SR-UKF and SR-UKFS are better, and the tracking accuracy of SR-UKFS is better than SR-UKF. Compared with the SR-UKF algorithm, the SR-UKFS algorithm can reduce nearly 59% of the position error and nearly 54% of the velocity error than the SR-UKF algorithm.

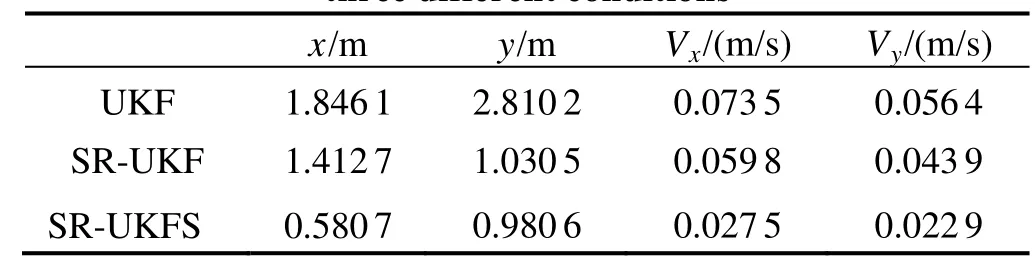
Tab.1 Comparison between RMS estimation variances of three different conditions

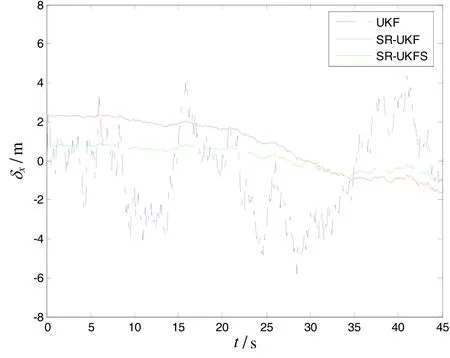
Fig.3 Estimation variance of location in line x

Fig.4 Estimation variance of location in line y

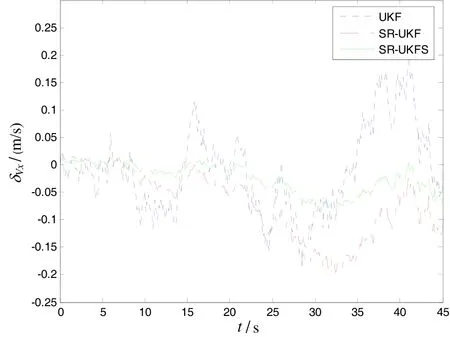
Fig.5 Estimation variance of speed in line x

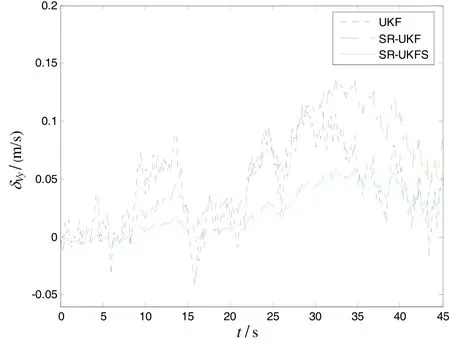
Fig.6 Estimation variance of speed in line y

4 Conclusion

In this paper, the author utilizes passive sonar to obtain the information of pitch angle and azimuth angle of underwater bearing-only target and track underwater motion targets by combination with the SR-UKFS algorithm. Based on SR-UKFS algorithm, better filtering effect can be achieved to enhance the tracking accuracy. The results of simulation show that SR-UKFS can be used in underwater motion target tracking, and the precision of filtering is significantly better than standard UKF and SR-UKFS algorithm.

[1] Hu Y F, Jiao B L. Passive underwater target motion analysis based upon bearing-elevation measurement in three dimensions[J]. Acta Simulate Systematica Sinica, 2003, 15(6): 776-779.

[2] Wu Pan-long, Wang Bao-bao, Cai Ya-dong, et al. Single observer passive target tracking based on extended H∞filter[J]. Journal of Chinese Inertial Technology, 2010, 18(5): 591-594.

[3] Wang Bo, Xu De-min, Shen Meng. Underwater passive target motion analysis based on UKF[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2005, 25(2): 423-426.

[4] Wu Pan-long, Wang Bao-bao, Ji Cun-hui. Design and realization of short range defence radar target tracking system based on DSP/FPGA[J]. WSEAS Transactions on System, 2011, 10(11): 376-386.

[5] Wang Bao-bao, Zhang Lian-zheng. Information Fusion of Airborne radar and ESM for maneuvering target tracking system based on IMM-BLUE[J]. WSEAS Transactions on System, 2014, 13(11): 699-707.

[6] Lefebvre T, Bruyninckx H, De Schutter J. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Trans on Automatic Control, 2000, 45(3): 477-482.

[7] Wu Pan-long, Kong Jian-shou. Under bearing-only target tracking based on Square-root UKF[J]. Journal of Nanjing University of Science and Technology (Natural Science), 2009, 33(6): 751-755.

[8] Rauch H E, Tung F, Striebel C T. Maximum likelihood estimates of linear dynamic systems[J]. AIAA Student Journal American Institute of Aeronautics & Astronautics, 1965, 3(8): 1445-1450.

[9] Cao Y, Mao X C. Improved filtering-smoothing algorithm for GPS positioning[C]//Proceedings of the 11th International IEEE Conference on Intelligent Transportation Systems. Beijing, China, 2008: 857-861.

[10] Zhang Fan, Wu Pan-long, Zhao Long-mei. Improved SRUKF algorithm for mobile robot tracking[J]. Journal of Computational Information System, 2012, 8(15): 6499-6506.

[11] Farina A. Target tracking with bearing-only measurements [J]. Signal Process, 1999, 78(1): 61-78.

[12] Yu Chun-lai, Zhan Rong-hui, Wan Jian-wei. Research on robust UKF algorithm for single observer passive target tracking based on polar coordinates[J]. Journal of National University of Defense and Technology, 2008, 30(5): 73-79.

[13] Sadhu S, Modndal S, Srinivasan M. Sigma point Kalman filter for bearing only tracking[J]. Signal Processing, 2006, 86(12): 3769-3777.

[14] van der Merwe R, Wan E A. The square root unscented Kalman filter for state and parameter estimation[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. New York, 2001: 3461-3464.

[15] Wu Pan-long, Liu Jia-le, Li Xing-xiu. Maneuvering target tracking in clutter background based on improved interacting multiple-model[J]. Journal Chinese Inertial Technology, 2015, 23(6): 755-762.

1005-6734(2016)02-0180-05

为了避免被动跟踪中非线性带来的计算复杂化及跟踪精度的下降，提出将平方根无迹卡尔曼滤波平滑算法（SR-UKFS）应用到水下纯方位目标跟踪。SR-UKFS利用Rauch-Tung-Striebel（RTS）平滑算法将平方根无迹卡尔曼滤波（SR-UKF）作为前向滤波算法得到的目标状态估计向后平滑，得到前一时刻目标状态估计，再利用该状态估计值进行再次滤波得到当前时刻目标状态估计。该算法得到的前一时刻的目标状态估计更加精确，从而进一步提高了目标跟踪的精度。最后，通过对SR-UKFS算法和SR-UKF算法的跟踪性能进行了对比分析和验证，仿真结果表明在相同条件下，SR-UKFS算法能减少59%的位置误差和54%的速度误差，SR-UKFS算法应用于水下纯方位目标跟踪系统是有效的，为水下纯方位目标跟踪系统的工程实现提供了非常有价值的参考。

目标跟踪；纯方位；平方根无迹卡尔曼滤波；平滑算法；前向滤波；后向平滑

A

2015-11-27；

2016-03-16

国家自然科学基金（61473153，61301217）

王宝宝（1985—），男，工程师，从事火控系统总体设计。E-mail: wangbaobao_zdh@126.com

10.13695/j.cnki.12-1222/o3.2016.02.008

基于平方根无迹卡尔曼滤波平滑算法的水下纯方位目标跟踪

王宝宝1，吴盘龙2

（1. 中国船舶重工集团第七一六研究所，连云港 222006；2. 南京理工大学 自动化学院，南京 210094）