重力扰动矢量对惯导系统影响误差项指标分析

王 晶，杨功流，李湘云，周 潇

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191；3. 东营职业学院 电子信息与多媒体系，东营 257091）

重力扰动矢量对惯导系统影响误差项指标分析

王 晶1,2，杨功流1,2，李湘云3，周 潇1,2

（1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 惯性技术国防重点实验室，北京 100191；3. 东营职业学院 电子信息与多媒体系，东营 257091）

针对制约现有惯导系统精度提升的重力扰动矢量误差项问题，从惯导系统误差模型入手，着重分析了重力扰动矢量水平分量（垂线偏差）在导航系统中的误差传播特性，利用简化的垂线偏差统计模型推导出导航系统位置误差均方差表达式；通过现有全球重力场高阶球谐模型（EGM2008），分析了垂线偏差全球均方差水平引起的惯导系统在典型载体运行速度下位置误差项大小，进而给出了垂线偏差补偿的误差项指标，在此基础上，分析了EGM2008在惯导系统中的适用性，结果表明，当EGM2008模型阶数小于12阶时才能满足导航系统计算资源要求，模型补偿精度为5.86″，适用于位置误差要求小于0.8 nm/h的惯导系统。

重力扰动矢量；惯导系统；位置误差均方根；EGM2008

随着惯性器件精度的提高，重力扰动矢量成为了制约惯性导航系统精度提升的主要误差源之一[1]。在全球范围内垂线偏差最大可达100″[2]（相当于500 μg），这一误差水平远高于现有加速度计零偏大小。因此，分析重力扰动矢量在惯导系统中的误差传播机理，明确其对导航系统定位精度影响的误差项指标，是实现高精度导航一项重要内容，并为后续的误差补偿研究提供支撑。

由于惯导系统高度通道解算常通过外部信息辅助完成，因此重力扰动矢量对惯导系统的影响主要表现在水平分量上[2-3]。国外关于重力扰动矢量对导航系统精度影响的研究工作始于20世纪70~80年代，主要利用重力格网数据以及垂线偏差统计模型进行地面慢速航行载体中惯导系统的位置误差分析。进入20世纪90年代后，主要针对机载INS/GPS组合的重力测量系统进行重力扰动矢量补偿及统计建模时的研究工作展开[3-5]，分析 GPS短时失锁时重力扰动对于惯导系统产生的影响[3]。国内的关于重力扰动对惯导系统的影响研究工作始于20世纪90年代初，但多针对特殊形式下的重力扰动传播规律进行静态仿真分析，结果对于实际的导航系统重力误差补偿与抑制并无指导性意义[6][7]。而对于重力补偿方面的研究，主要集中于利用GPS等外部信息辅助的重力扰动在线估计或已知重力区域数据的补偿等方法层面的探索[8-9]。针对导航系统的实际使用需求，文献[10]首次分析了适用于不同运动速度载体的补偿时间间隔。目前，尚未出现具体补偿误差项指标的专项研究工作。

本文结合高阶重力场球谐模型EGM2008，定量分析了重力扰动水平分量引起的导航位置误差均方根大小，明确典型载体运行速度下重力扰动补偿的误差项指标，并分析采用EGM2008模型进行误差补偿手段的适用性，取得的结论具有工程参考价值。

1 重力扰动矢量建模

1.1 重力扰动矢量定义

重力扰动（异常）矢量定义为大地准面上一点在参考椭球表面上对应位置的实际重力值（gp）与椭球上正常重力值（γQ）的差值[11]，如图1所示。

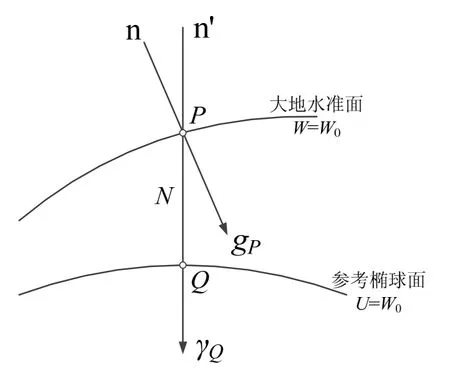
图1 重力扰动矢量定义Fig.1 Definition of gravity disturbance vector

其大小定义为重力扰动（δg）（或重力异常Δg），方向定义为垂线偏差（包括东西向和南北向两个分量，η和ξ），同时，垂线偏差又可以描述这球面上一点的天文坐标与大地坐标下点的铅垂线的差[12]，如图2所示。

因此，重力扰动矢量在惯导系统中可以表述为：

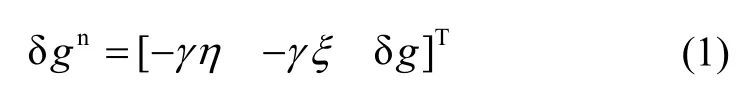
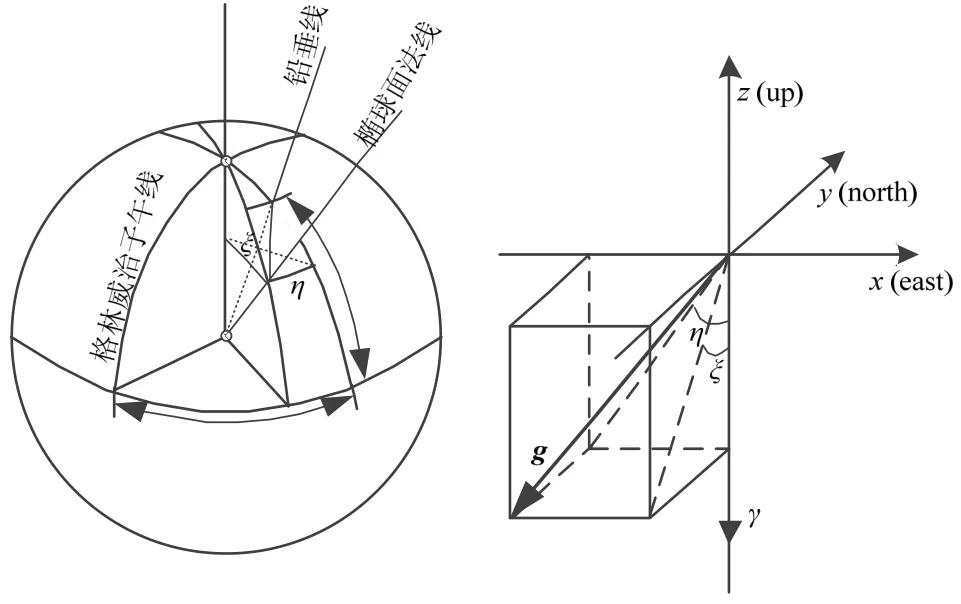
图2 垂线偏差定义Fig.2 Definition of vertical deflection

其中，γ表示正常重力。

1.2 确定性模型

在位场理论中，重力加速度表示为重力势能的梯度，而重力扰动矢量则为扰动位在大地坐标系下的三个分量。通常以球谐级数模型表达扰动位：

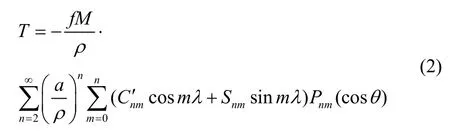
式中：f为引力常数；M表示地球质量；a表示地球赤道半径；ρ表示点的向径；n为调和项阶数；m为调和项次数；λ表示经度；θ表示余纬，即θ=90°-φ，φ表示纬度；Pnm表示缔合勒让德函数；C'nm与Snm为调和系数，C'nm为椭球参数修正后的调和系数，采用精密的地球重力卫星测量数据以及地面测量数据计算得到。

对上述扰动位对大地坐标求导数，即得到重力扰动矢量的三个分量：

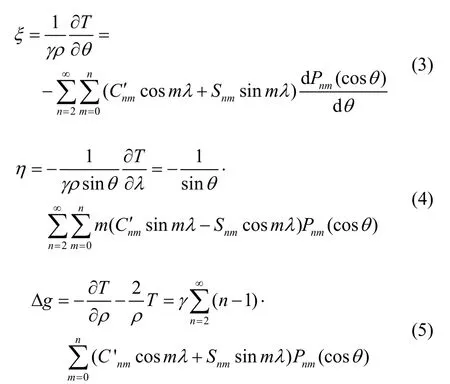
为方便计算与表示，式(5)中以重力异常代替重力扰动。

2 重力扰动矢量引起的位置误差

重力扰动对惯导系统的影响主要体现在水平通道的影响上，即垂线偏差引起的水平通道误差，如图 3所示的静基座东向通道误差方块图。在系统初始对准后，不可避免地存在平台误差倾角φ，由此将使水平回路中引入交叉耦合加速度误差aR，这个误差即为重力反作用力，而耦合的加速度误差又引起了速度、位置以及附加的倾角误差。垂线偏差就可以视为平台倾角误差来进行导航误差分析。

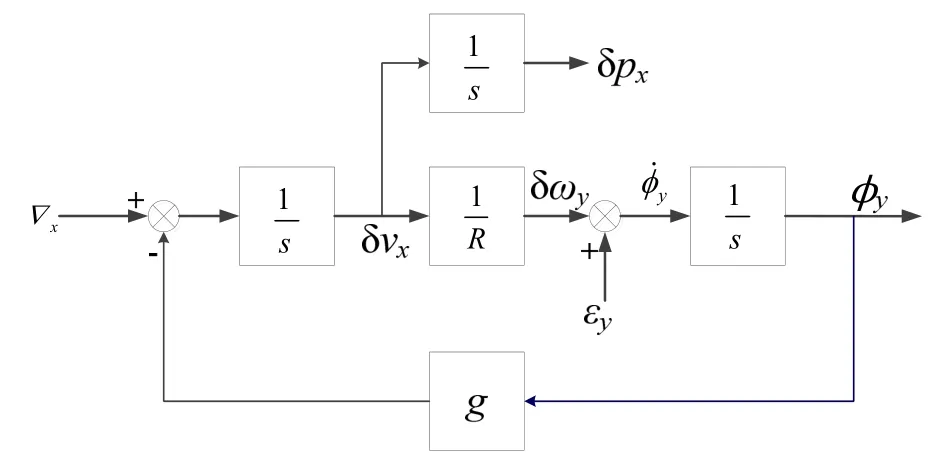
图3 惯导系统水平通道误差方块图Fig.3 Horizontal channel error in inertial navigation system

经过误差修正的惯导系统重力模型为：

忽略其它误差，重力扰动在水平方向引起的惯导系统位置误差传递函数可以简化为：

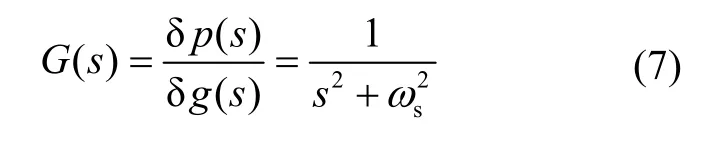
式中，ωs=为舒勒频率。据此得到以重力扰动激励的水平位置误差时域表达式如下：

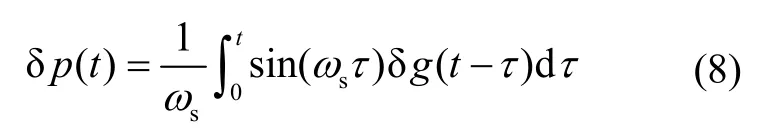
由于重力扰动是一个时变函数，不妨假设为均值为零的平稳随机过程，对式(8)取数学期望，就得到了位置误差的均方误差：

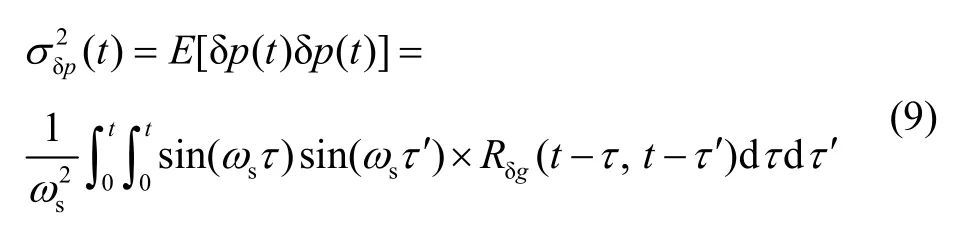
式中，Rδg(t-τ, t-τ')为水平重力扰动分量的自相关函数。为了方便分析，假设具有如下一阶马尔可夫形式：

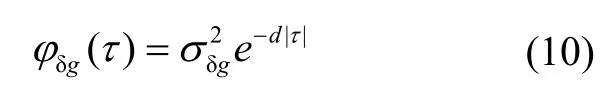
因此，得到考虑了重力扰动的惯导系统位置误差均方差：

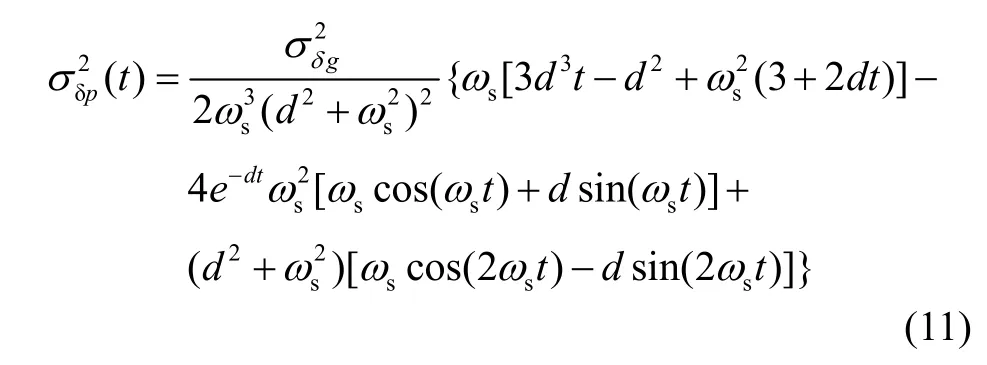
根据式(11)，代入重力扰动误均方差、载体速度、相关距离就可以确定重力扰动引起的位置误差量级。

3 导航位置误差项指标分析

3.1 垂线偏差全球均方差

由式(11)可以看出，重力扰动水平分量引起的位置误差方差的大小与扰动的方差成正比，因此，垂线偏差的方差大小直接决定位置误差的量级。这里我们采用1.2节给出的确定性模型进行定量分析，垂线偏差的全球均方差可以由下式计算：

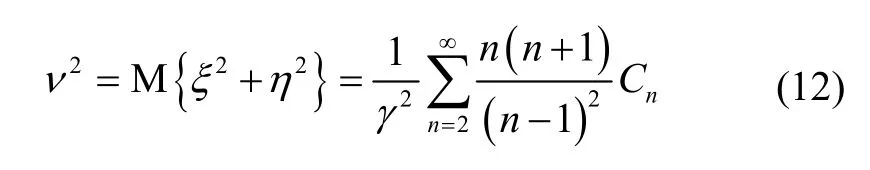
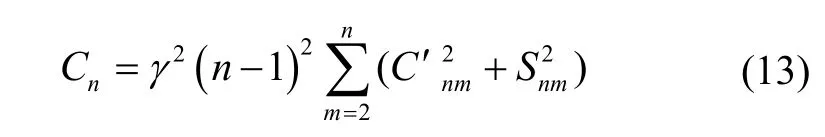
由此，根据EGM2008重力场模型提供的调和项系数可以得到垂线偏差阶方差对全球均方差的贡献量如图4所示。

式中：M{•}为求平均的代数运算；Cn为重力异常阶方差[13]，

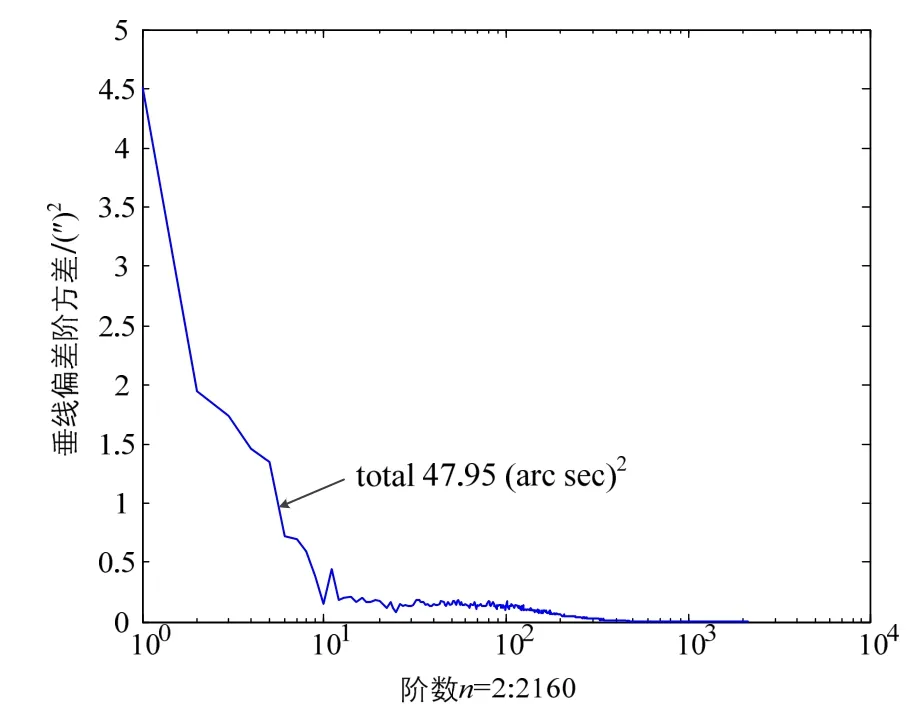
图4 垂线偏差阶方差Fig.4 Degree variance of vertical deflection

根据EGM2008重力模型提供的2160阶系数值可得，重力异常全球均方根误差为±35.14 mGal，垂线偏差全球均方根为±6.9″（相当于±32.7 mGal）。因此将这一垂线偏差水平代入式(11)中，即得到与载体速度和相关距离有关的位置误差均方根曲线。图5和图6分别给出了垂线偏差引起的1 h导航位置误差与载体速度和相关距离的关系。

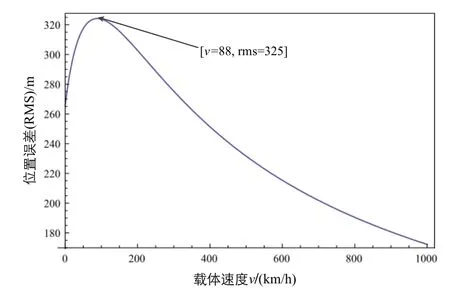
图5 D=20 nm时位置误差与载体速度关系Fig.5 Relationship of velocity and position error (D = 20 nm)

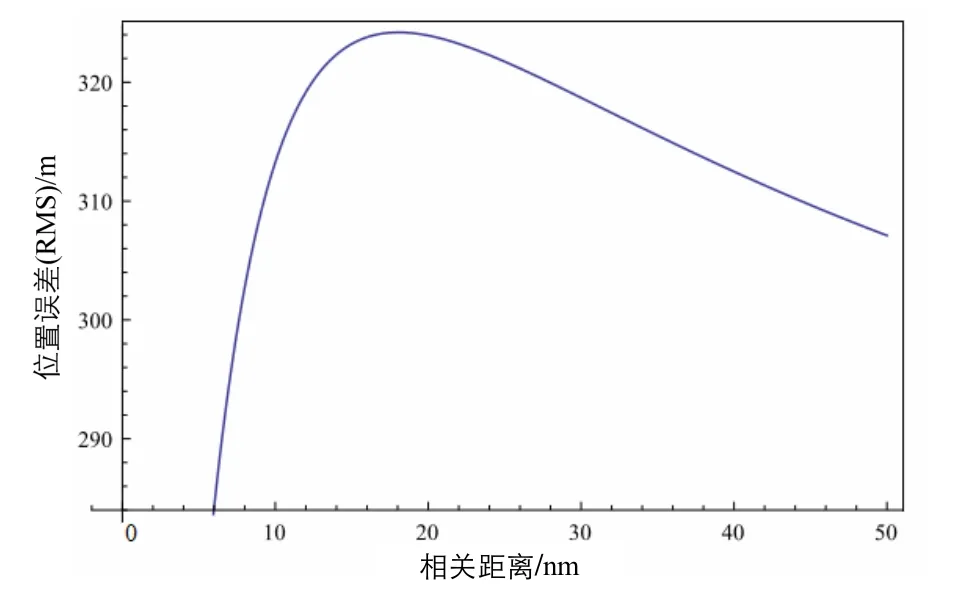
图6 v = 80 km/h时位置误差与相关距离关系Fig.6 Relationship of correlation distance and position error (v = 80 nm/h)

从图5~图6中的结果可以看出：当载体速度大于88 km/h后，随着速度的提高，垂线偏差引起的位置误差呈减小趋势；另一方面，当相关距离大于 18 nm时，位置误差同样随相关距离的增大而减小，通常情况下，重力扰动矢量相关距离为20 nm。

3.2 位置误差项指标

从图7所示的结果可以看出，垂线偏差引起惯导系统位置误差随时间累积，且呈线性震荡增长。进一步计算得到，v=40 km/h时，RMS=0.17 nm/h；v=80 km/h时，RMS=0.18 nm/h；v=400 km/h时，RMS=0.14nm/h；v=1000 km/h时，RMS=0.09 nm/h。因此，得到在特定运行速度下垂线偏差对不同精度级别惯导系统的位置误差贡献率如表1所示。

从表1的结果可以看出，对于水面、陆地上的低速运行载体，垂线偏差的影响较大。以20%的误差贡献率为指标的情况下，我们认为表中加粗的误差项需要补偿。进而得出若使垂线偏差的误差贡献率满足指标要求，对惯导系统进行重力扰动矢量误差补偿所需要达到的精度指标如表2所示。

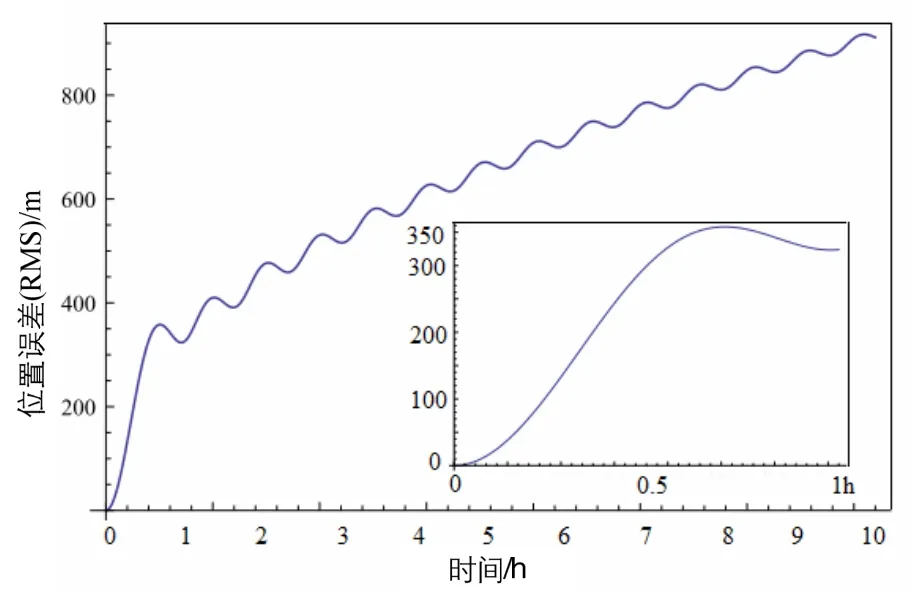
图7 垂线偏差引起的导航位置10 h误差RMSFig.7 RMS of position error induced by vertical deflection in 10 h

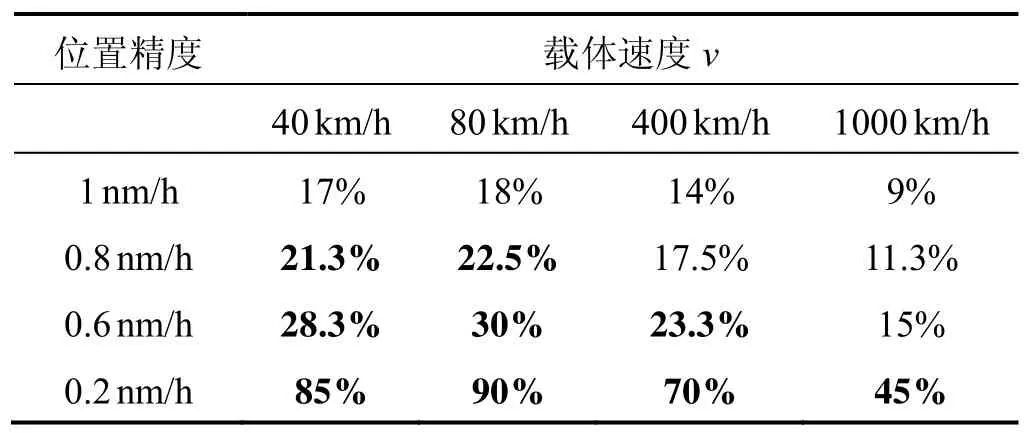
表1 垂线偏差对惯导系统位置误差贡献率Tab.1 Contribution rate of vertical deflection to position error of INS

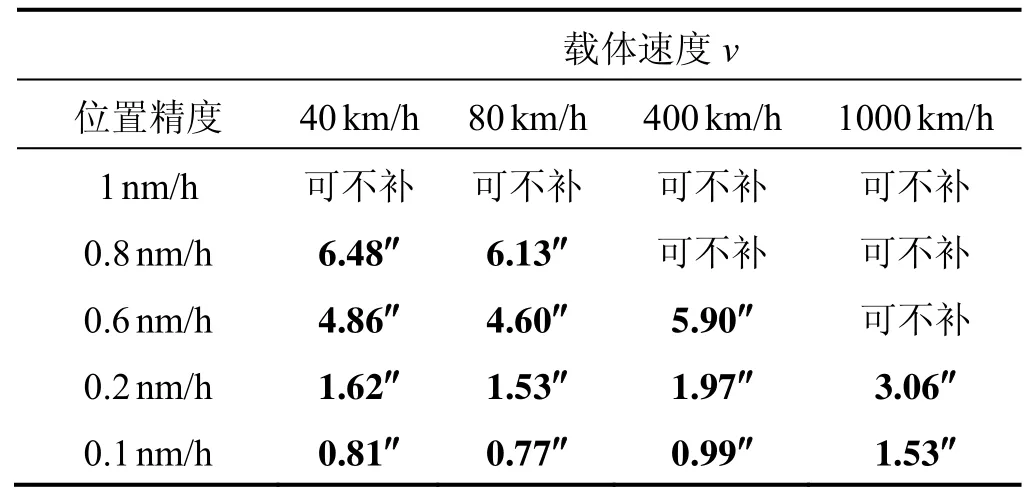
表2 残余垂线偏差容许值Tab.2 Threshold value of residual vertical deflection

从表2中可以发现，对于0.2 nm/h位置精度级别的惯导系统来说，除超音速飞行器重力扰动矢量误差补偿精度均应达到2″以上。

4 EGM2008模型适用性分析

4.1 球谐级数模型谱分析

基于以上对导航系统的要求，分析现有高阶EGM2008对于精度的满足性。已知重力异常阶方差表达式(13)和如下重力异常误差阶方差：代入EGM2008模型系数值级系数误差方差值，可得如图8所示的阶方差曲线。

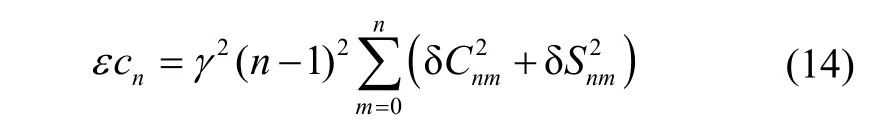
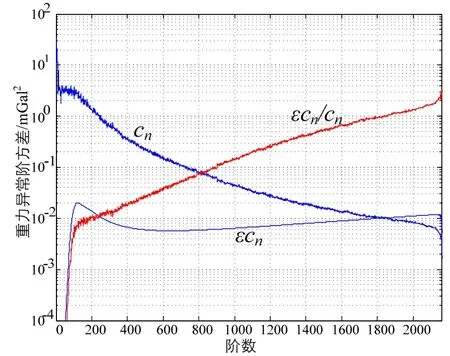
图8 重力异常信号阶方差及误差阶方差Fig.8 Degree variances of signal and its error of gravity anomaly

从图8可知，当模型阶数n为1833时，误差阶方差和信号阶方差的比值接近为 1，认为过此点的模型系数不可信。为了得到较高精度的计算结果，我们选取比值在0.1以下的模型作为研究对象，因此，将模型截断至n=900阶，由此产生的截断误差为1.06″。再考虑约0.5″的位系数误差累积影响，截断至900阶时，按模型计算得到的垂线偏差均方根误差将达到1.56″。对照表2的残余误差容许值可以发现，对于用于速度小于 400 km/h载体的 0.2 nm/h精度级别惯导系统来说，单纯的模型误差补偿往往不能够满足要求。

4.2 球谐级数模型计算用时测试

从计算量角度分析，球谐级数模型的时间复杂度为O(n2)，计算用时随着阶数的增长而呈平方递增。图9给出了球谐模型在典型 DSP（TMS320C6713，256K×16-bit flash）中的运行结果。

我们发现，当模型阶数大于12阶时，模型计算用时已经达到1 ms，在导航系统中解算周期一般配置为2.5~10 ms之间，显然，高阶球谐模型不能满足惯导系统的高速计算。

从存储空间角度分析，以float型存储为例，n阶球谐模型需要存储包括球谐系数、勒让德函数参数等参数共计2(n+4)(n-1)个，不同阶数模型占用存储空间大小如表3所示。

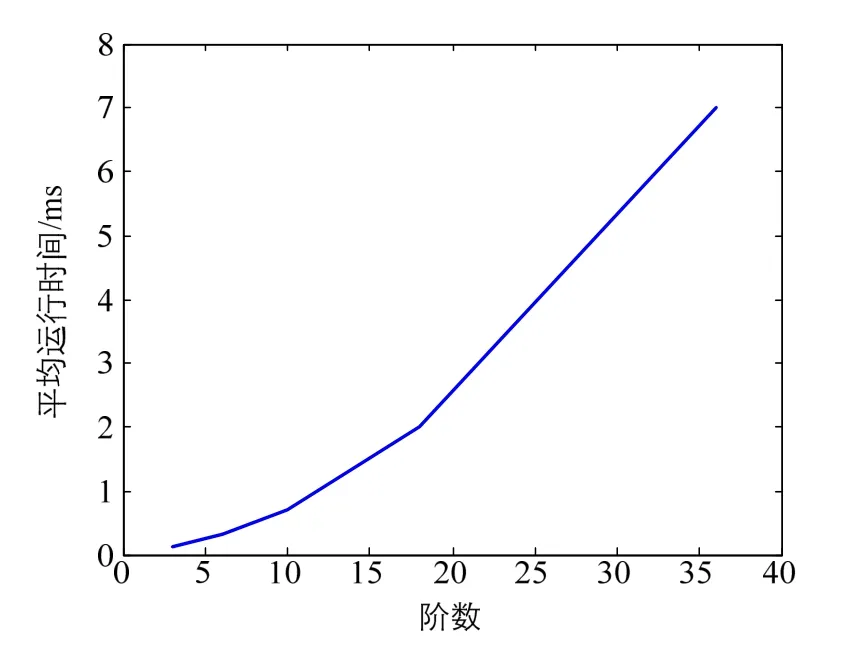
图9 各阶次球谐模型计算用时Fig.9 Average execution time for spherical harmonic model of a given degree and order

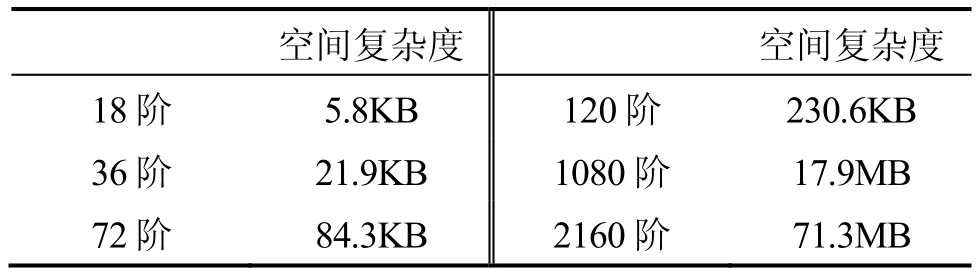
表3 不同阶数球谐模型空间复杂度Tab.3 Space complexity for spherical harmonic model of a given degree and order

当把72阶球谐模型用于DSP中参与导航解算时，将出现溢出存储的错误（这是因为DSP还将为导航解算留出计算空间），因此，高阶球谐模型并不适用于传统导航系统的硬件配置环境。

综上所述，在现有惯导系统硬件配置的基础上，只有12阶以下的EGM2008模型能够适用导航系统解算。根据式(12)，12阶球谐模型所产生垂线偏差截断误差约为 5.86″，对照表 2并考虑位系数误差累积影响，12阶球谐模型适用于位置精度为0.8 nm/h的低速运行载体（如地面、水面或水下载体）以及部分位置精度在0.6 nm/h以上的航空载体。

5 结 论

本文针对重力扰动矢量对高精度惯导系统位置误差影响问题进行深入分析，建立了水平重力扰动分量激励的导航位置误差均方差表达式，明确了位置误差均方差与载体速度、重力扰动矢量相关距离的关系以及长航时导航位置误差震荡增长的特性。在此基础上，根据现有高阶重力场球谐模型EGM2008的全球均方差大小，明确不同载体运行速度下垂线偏差占导航系统误差总量的比例关系，进而得到以20%的误差贡献率为指标的条件下惯导系统垂线偏差补偿指标，认为当载体运行速度低于400 km/h时，全阶次EGM2008模型只能满足位置误差大于0.2 nm/h，当载体运行速度大于1000 km/h时全阶模型可以满足导航位置精度至 0.1 nm/h。最后在现有惯导系统典型硬件配置环境下进行EGM2008模型的适用性测试，证明了12阶球谐模型可以满足导航系统实时解算要求，误差补偿精度约为5.86″。

（References）：

[1] Siouris G M. Gravity modeling in aerospace applications [J]. Aerospace Science and Technology. 2009: 301-315.

[2] Kopcha P D. NGA gravity support for inertial navigation [C]//ION 60thAnnual Meeting. Dayton, USA, 2004: 497-504.

[3] Jekeli C. Gravity on precise, short-term, 3-D free-inertial navigation[J]. Journal of the Institute of Navigation, 1997, 44(3): 347-357.

[4] Grejner-Brzezinska D A, Yi Y, Toth C. Enhanced gravity compensation for improved inertial navigation accuracy [C]//ION GPS/GNSS. Portland, 2003: 2897-2909.

[5] Cai Shao-kun, Zhang Kai-dong, Wu Mei-ping. Improving airborne strapdown vector gravimetry using stabilized horizontal components[J]. Journal of Applied Geophysics. 2013, 79-89.

[6] 尧颖婷, 沈晓蓉, 邹尧, 等. 捷联惯性导航系统重力扰动影响分析[J]. 大地测量与地球动力学, 2011, 31(6): 159-163. Yao Ying-ting, Shen Xiao-rong, Zou Yao, et al. Analysis of gravity disturbance influence on strapdown inertial navigation system[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 159-163.

[7] 赵忠, 王鹏. 高精度惯性导航系统垂线偏差影响与补偿[J]. 中国惯性技术学报, 2013, 21(6): 701-705. Zhao Zhong, Wang Peng. Analysis and compensation of vertical deflection effect on high accuracy inertial navigation system[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 701-705.

[8] Fang Jiancheng, Chen Linzhouting, Yao Jifeng. An accurate gravity compensation method for high-precision airborne POS[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 8: 1-10.

[9] 周潇, 杨功流, 王晶, 等. 基于 Kalman滤波原理对惯导中重力扰动的估计及补偿方法[J]. 中国惯性技术学报, 2015, 23(6): 721-726. Zhou Xiao, Yang Gong-liu, Wang Jing, et al. Estimation and compensation for gravity disturbance based on Kalman filtering in inertial navigation[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 721-726.

[10] Wang Jing, Yang Gong-liu, Li Xiang-yun, et al. Research on time interval of gravity compensation for airborne INS [C]//Proceedings of the 34th Chinese Control Conference. China, 2015: 5442-5446.

[11] Wellenhof B H, Moritz H. Physical geodesy[M]. 2ndEd. Graz, Austria: Springer-Verlag Wien, 2005: 90-96.

[12] Soler T, Han Jen-Yu, Weston N D. On deflection of the vertical components and their transformations[J]. Journal of Surv. Eng., 2014, 140: 1-15.

[13] 翟振和, 任红飞, 孙中苗. 重力异常阶方差模型的构建及在扰动场元频谱特征计算中的应用[J]. 测绘学报. 2012, 41(2): 159-164. Zhai Zhen-he, Ren Hong-fei, Sun Zhong-miao. Construction of gravity anomaly degree variance model and application in computation of spectral sensitivity of disturbing gravity functions[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 159-164.

Error indicator analysis for gravity disturbing vector’s influence on inertial navigation system

WANG Jing1,2, YANG Gong-liu1,2, LI Xiang-yun3, ZHOU Xiao1,2
(1. School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing 100191, China; 2. Science and Technology on Inertial Laboratory, Beijing 100191, China; 3. School of Electronic Information and Media, Dongying Vocational College, Dongying 257091, China)

The characteristics of gravity disturbing vector errors and their influences on navigation algorithm are studied for suppressing the navigation errors. Based on the error model of the inertial navigation systems (INS), the position error excited by horizontal component of gravity disturbing vector is studied, and according to which, the position RMS is derived. The global average variance of vertical deflection is used to quantify the vertical-deflection-induced position RMS under different velocities of vehicle set. Then the indexes of vertical deflection influencing on INS are proposed. Experiments with digital signal processor show that the requirements of computing resources of the navigation system can only be satisfied when with＜12-order spherical harmonic gravity model EGM2008, and the compensation precision of the model is 5.86″. This gravity model can be applied to such INS as the position error is ＜0.8 nm/h.

gravity disturbing vector; inertial navigation system; position RMS; EGM2008

U666.1

：A

2016-03-30；

：2016-04-12

国家自然科学基金资助项目（61340044）；中央高校基本科研业务费专项资金资助项目（YWF-10-01-B30）

王晶（1987—），女，博士研究生，从事重力场建模技术研究。E-mail: 050441jj@163.com

联 系 人：杨功流（1967—），男，教授，博士生导师。E-mail: bhu17-yang@139.com

1005-6734(2016)03-0285-06

10.13695/j.cnki.12-1222/o3.2016.03.002