未知纬度条件下基于重力视运动与小波去噪的SINS自对准方法
2016-04-13刘锡祥黄永江
刘锡祥,杨 燕,黄永江,宋 清
(1. 微惯性仪表与先进导航技术教育部重点实验室,南京 210096;2. 东南大学 仪器科学与工程学院,南京 210096)
未知纬度条件下基于重力视运动与小波去噪的SINS自对准方法
刘锡祥1,2,杨 燕1,2,黄永江1,2,宋 清1,2
(1. 微惯性仪表与先进导航技术教育部重点实验室,南京 210096;2. 东南大学 仪器科学与工程学院,南京 210096)
基于惯性系的双矢量定姿方法选择惯性系中的两个重力视运动向量作为不共线矢量,解决了传统双矢量定姿方法在晃动基座条件下易受载体角运动干扰而无法实现对准的问题,但该方法仍需要精确的地理纬度信息以参与对准计算。针对未知纬度条件下的SINS抗晃动自对准问题,提出了一种基于重力视运动的三矢量自对准方法。该方法将初始对准问题归结为求解当前时刻导航系相对于初始时刻载体系的姿态矩阵问题,并利用矢量运算进行求解,仿真结果表明:加速度计随机测量噪声会映射为重力视运动随机噪声,降低对准精度;当加速度计随机噪声量级较大时,会带来对准计算失败。针对噪声问题,引入Daubechies(db4)小波进行5层分解来实现对重力视运动的降噪,并选择去噪后的重力视运动向量参与三矢量定姿解算,仿真结果表明:db4小波具有良好的去噪效果,基于小波去噪的三矢量自对准方法可以有效完成未知纬度条件下的SINS初始对准。
捷联式惯性导航系统;初始对准;重力视运动;小波去噪;三矢量定姿
初始对准是捷联式惯性导航系统(SINS)导航工作 的前提和基础。一般而言,SINS的初始对准具体指:构建数学平台,并使其重合于预设的导航坐标系,同时获取载体系相对于导航系的实时姿态矩阵[1-2]。经过数十年的发展,在 SINS的初始对准方面有着许多成熟方法,如:基于双矢量定姿的解析对准方法[3],基于罗经效应的罗经对准方法[4],基于载体运动约束的零速对准以及基于外部参考信息与最优估计的传递对准等[5]。然而上述方法一般都需要精确的纬度信息加以辅助,如:解析对准中需要纬度信息分解地球自转角速度,罗经对准以及传递对准中需要纬度信息参与导航解算[6],但是在诸如隧道、桥下、深海等特殊情况下,想要获取精确的纬度信息却并非一件容易的事。针对这种情况,寻找一种方法来实现未知纬度条件下的初始对准显得十分必要。
近年来,为解决晃动条件下的初始对准问题,基于惯性系的初始对准方法受到了一定程度的关注。文献[7-8]提出了摇摆基座上基于重力加速度信息的SINS粗对准方法,该方法将初始载体坐标系凝固为惯性坐标系,将姿态矩阵进行链式分解,通过观察惯性系中的重力加速度漂移,具体实现了晃动条件下的初始对准,并通过积分运算平滑了加速度以提高对准精度。一般而言,当前基于惯性系的对准方法均选择双矢量定姿算法作为数学工具。该类对准方法在有效地隔离晃动干扰的同时,仍需要有精确的纬度信息加以辅助。
受到惯性系中各重力视运动向量间几何关系的启发,本文提出了一种基于重力视运动的三矢量法的SINS自对准方法,以解决未知纬度条件下的晃动基座对准问题。该方法是利用三个不共线的重力视运动向量求取重力视运动锥体底圆中心,并进一步通过矢量运算求出其当前的姿态矩阵。针对该方法对准精度易受到加速度计测量噪声影响的问题,本文进一步引入db4小波对重力视运动向量进行预处理以去除噪声。仿真结果表明,经过小波去噪改进后的三矢量法的SINS自对准方法可以很好地实现未知纬度条件下的晃动基座对准问题。
1 基于重力视运动与矢量运算的SINS自对准算法
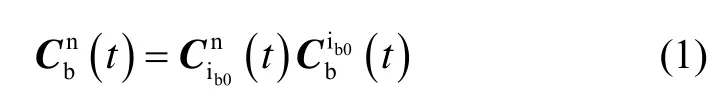
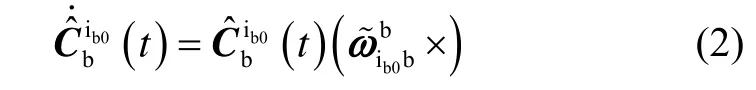
综合公式(1)和公式(2)可知:只要获取了惯性坐标系和当前导航坐标系之间的姿态矩阵(t ),通过链式法则,即可获得姿态矩阵(t)完成初始对准。
1.1 惯性系中的重力视运动
视运动最初用来描述陀螺仪的定轴性。陀螺的视运动具体指:在随地球自转的导航系中观察到的相对于惯性空间稳定的自由陀螺仪的指向变化。不同于陀螺的视运动,本文定义重力视运动为:在惯性系中观察到的随地球自转的导航系中重力加速度的指向变化。根据文献[9]可知,惯性系的重力视运动可以描述为图1所示的圆锥,锥顶位于地球球心,圆锥的中心轴与地球的自转轴重合,锥体的底圆半径由载体所在的纬度决定。
1.2 基于三个重力视运动向量的SINS自对准算法
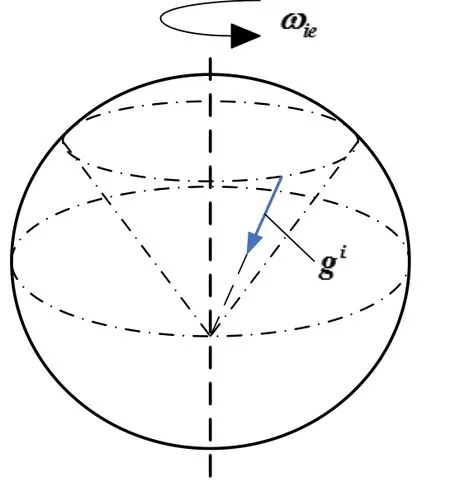
图1 惯性系中的重力视运动Fig.1 Apparent motion of gravity in inertial frame
本文分别采用“东北天ENU”与“右前上”为导航坐标系和载体坐标系。由惯性系中重力视运动的描述,可以将导航坐标系与重力视运动形成的锥体之间的几何关系描述为图2,其中点O表示地球球心,点Oc表示底面圆锥的圆心,其与载体所在位置纬度圈的圆心重合,并且位于地球的自转轴上。在t时刻,导航系的原点为圆锥底圆圆周上的点On,向量与导航系的天向轴U重合,但与重力加速度在惯性系投影值gi(t)的方向相反,向量与地球自转轴ωie重合,的叉乘积与导航系的东向轴E重合,U×E的叉乘积又与导航系的北向轴N重合。若已知导航系的各轴在惯性系的投影值,则可以通过下式求得矩阵 C(t):
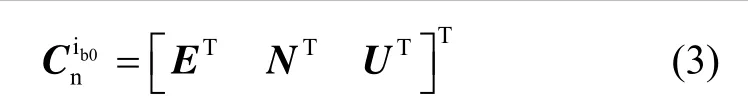
式中,E、N、U分别表示导航系各轴在惯性系的投影值。
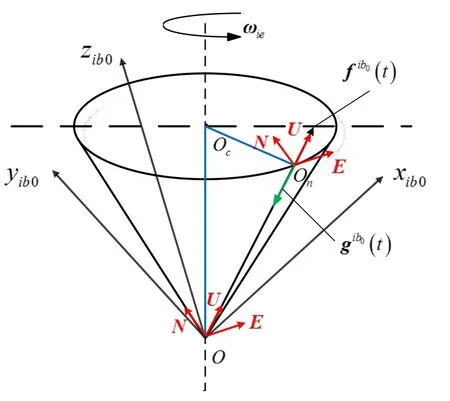
图2 基于重力视运动的对准机理Fig.2 Alignment mechanism based on gravitational apparent motion
基于上述分析,完成初始对准的关键在于获取导航系各轴在惯性系中的投影值。因而,完成初始对准的关键步骤可以归结为:1)在惯性系中构建重力视运动向量;2)利用重力视运动向量求解导航系各轴在惯性系的投影值,并进一步求解Cnib0(t)。不考虑仪表安装误差,假设惯性测量组件坐标系与载体坐标系重合,则惯性系中的重力视运动向量可以用下式构建:
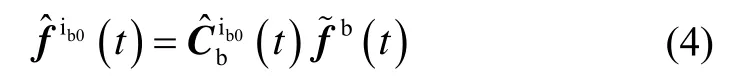
为了获得导航系各轴在惯性系中的投影值,需要获取视运动锥体底圆圆心 Oc点的坐标(x0,y0,z0)。如图3所示,假设三个不同时刻 tA、tB、tC的重力视运动向量分别为,各向量的计算值可理解为相应时刻的重力视运动向量在锥体底圆上的坐标值,分别为(x3,y3,z3)。根据解析几何知识可求得向量的中垂线,两条中垂线的交点即为圆锥底圆圆心 Oc,具体可以描述如下:
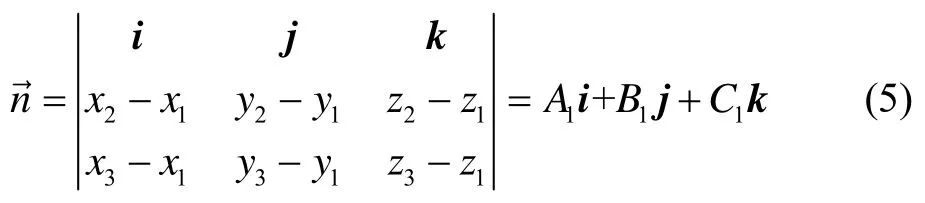
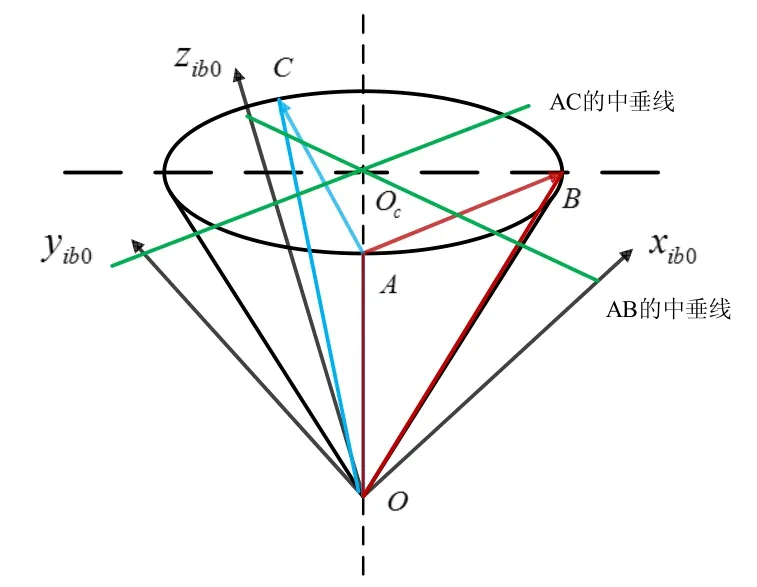
图3 锥体底圆圆心的求取Fig.3 Calculation method for cone axis
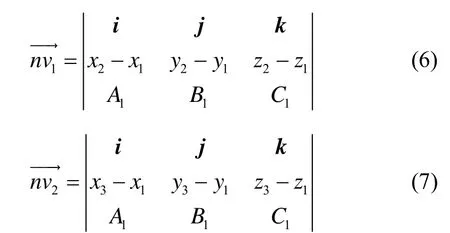
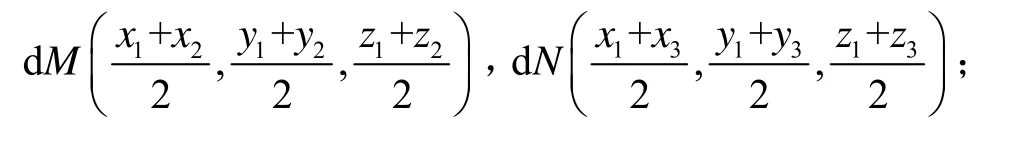
AB的中垂线方程为:
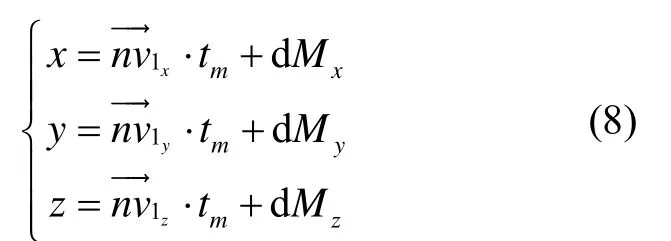
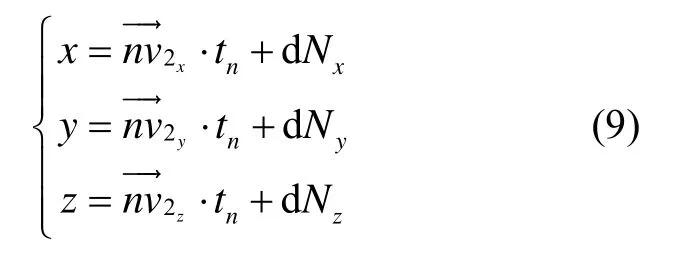
3)求得圆心坐标(x0,y0,z0)联立方程(8)(9)可以求得:
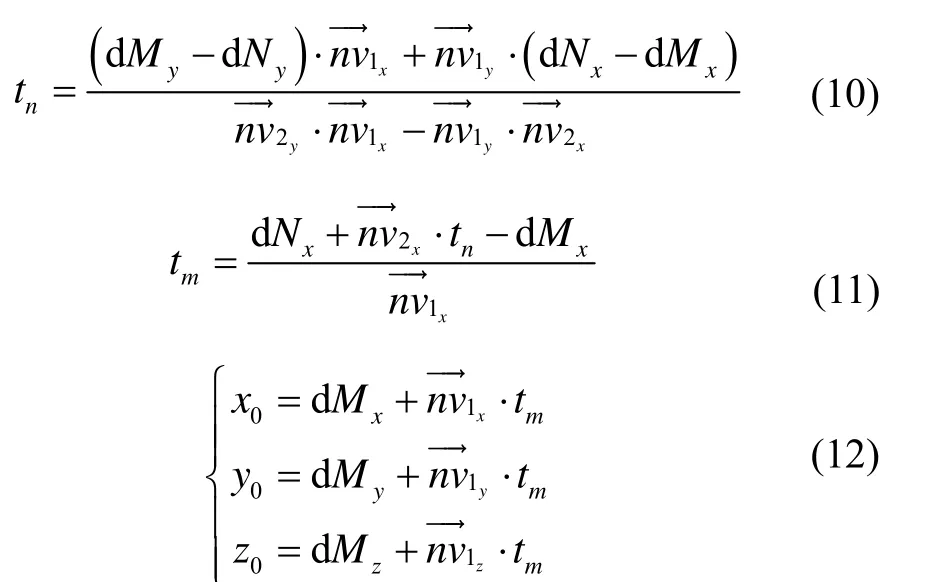
c
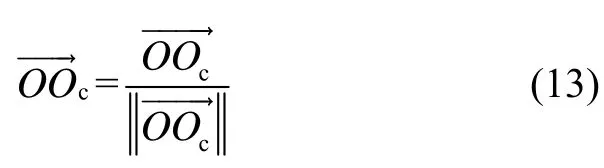
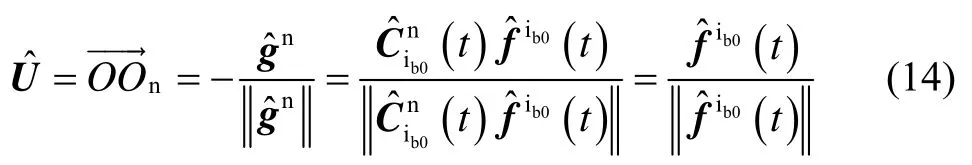
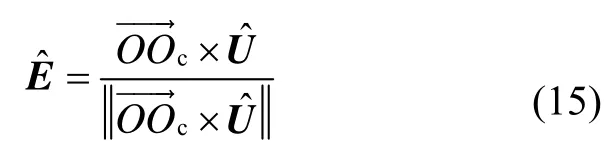
最后,向量N可以通过下式获取:

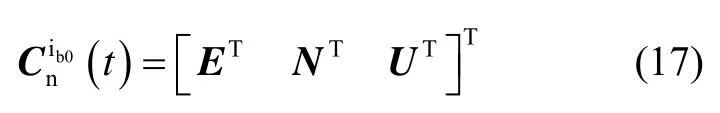
进一步,可根据式(1)(2)(17)完成初始对准。该方法可获取的理论最小对准误差可表达如下:
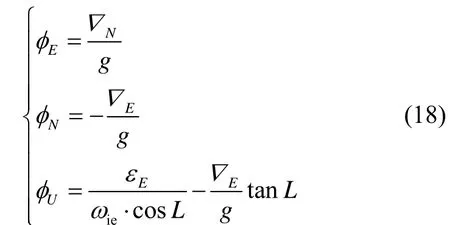
1.3 仿真验证
1.3.1 仿真条件设置
以舰船为例,为了方便分析,我们首先考虑舰船在静基座情况下的对准情况,表1为仿真条件,表2为传感器误差参数。
在第一种条件下,舰船处于静止状态且仪表仅存在常值误差而无随机误差,这种情况在现实中是不存在的,此处作为理论分析。
设仪表数据的采样频率为200 Hz,导航解算的更新周期为5 ms。根据舰船运动,通过逆向导航解算可反演得到仪表的理想输出值;在理想输出上叠加上表2中的各误差后,可模拟仪表的真实输出;同时可利用舰船运动参数作为评价标准,以计算对准误差。根据公式(18)以及表 2中的仪表误差参数可以计算出纵摇、横摇与航向的理论的最小对准误差分别为0.0029°、-0.0029°、0.2228°。

表1 仿真条件Tab.1 Simulation conditions
表2 仪表误差参数Tab.2 Sensor errors
1.3.2 仿真结果及分析
仿真持续600 s。系统选择了0 s、2.5 s、5 s三个时刻的重力视运动向量以 5 s一个周期进行一次完整的三矢量对准。对准误差如图4所示,虚线代表的是第一种条件下的对准误差,实线代表的是第二种条件下的对准误差。对准误差的统计结果如表3所示。
由图4的对准误差曲线可知:当惯性测量元件的测量值中不含有随机误差的时候,基于重力视运动的三矢量对准方法可以有效地完成未知纬度条件下的SINS初始对准,对准精度与理论精度值相当。但是当仪表的测量数据中存在随机误差时,航向对准无法完成,且水平(纵摇和横摇)对准结果中含有较多的毛刺,与理论精度间存在较大的差异。
显然两种条件的区别仅在于仪表测量值中有无随机噪声。因陀螺仪的测量噪声在积分过程中得到平滑,可以认为加速度计测量值中的随机噪声是导致第二种条件对准失败的主要原因,该噪声被投影为重力视运动向量中的随机噪声,从而导致导航系各轴在惯性系中投影值的计算精度下降。进一步针对摇摆基座条件下的仿真验证将在解决噪声干扰问题后进行。

表3 对准误差统计结果Tab.3 Statistics of alignment error
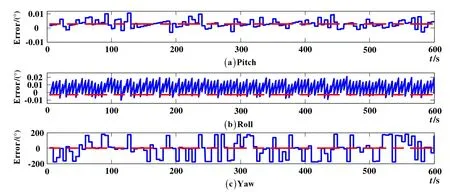
图4 对准误差曲线Fig.4 Curves of alignment errors
2 基于小波去噪的SINS自对准改进方法
2.1 重力视运动向量的预处理
第1节分析表明,与惯性系中的双矢量定姿算法类似[10-11],基于三矢量定姿 SINS自对准方法的对准精度主要取决于加速度计的测量精度,尤其是加速度计测量值中随机噪声的影响。该噪声带来了两个主要问题:1)惯性系中的重力视运动向量不能真实地反映重力漂移;2)选取的重力视运动向量可能存在共线问题。文献[12-13]分析表明,要避免重力视运动向量间的共线,一是加大时间间隔,二是提高重力视运动的计算精度。但前者会带来对准时间的冗长。基于此,本文着力解决重力视运动向量的计算精度问题。
近年来,针对噪声问题涌现了许多成熟的数学方法,小波去噪是一类典型代表。小波变换相对于传统的傅里叶变换具有对信号良好的时频局部刻画性能,它能够在去除大部分噪声的同时,保留信号的瞬态特征,本文选取了db4小波来对重力视运动向量进行去噪。
1)小波去噪原理
小波理论的迅速发展以及其良好的时频特性,使其应用领域越来越广泛,其中信号和图像的降噪与压缩是小波的重要应用之一。
在现实环境中,信号的传输与收集总是不可避免地会受到一些噪声的影响。一个含噪的一维信号模型可以表示为如下形式:
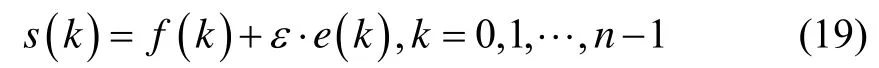
式中, s(k)为含噪信号, f(k)为有用信号, e(k)为噪声信号。这里我们考虑 e(k)为一个1级高斯白噪声,通常表现为高频信号,而在实际的工程应用中, f(k)通常表现为低频信号或者是一些比较平稳的信号。因此可以将小波去噪的原理描述如下:首先对原始信号进行小波分解,由于噪声信号大多包含在具有较高频率的细节中,因而可以通过门限阈值等形式对分解的小波进行处理,然后对处理后的信号进行重构即可达到去噪的目的[14-17]。对信号的降噪实质上就是抑制原信号中的无用部分恢复其中的有用部分。
2)小波降噪的步骤和方法
一般而言,一维信号的降噪过程可以分为以下三个步骤:
① 分解过程:选定一种小波,对信号进行N层小波(小波包)分解;
② 作用阈值过程:对分解得到的各层系数选择一个阈值,并对细节系数作用软阈值处理;
③ 重建过程:降噪处理后的系数通过小波(小波包)重建恢复原始信号。
在小波去噪的三个过程中,最重要的一步是阈值的选择以及如何进行阈值量化,本文中选择了分层的软阈值方法对原始信号进行降噪处理,其基本原理是根据方差最小的原则通过对系数的无偏似然估计来确定阈值。采用分层阈值的处理方法虽然会遗失原始信号的部分性能,但是去噪后的信号要比全局阈值的结果光滑许多,并且能够最大限度地反映原信号本身的性质。
3)仿真验证
本文采用了db4小波,分解层次设置为5层,对重力矢量投影值进行去噪。仿真过程持续600 s,仿真条件是在表1的第二种条件下进行的,图5中实线代表的是去噪前的惯性系各轴的重力视运动向量值,虚线是db4小波进行5层分解,通过分层阈值的方式得到的去噪后的重力视运动向量值。从图5可以看出,小波去噪可以有效地去除仪表测量值中的随机噪声,较好地保留了有用信号。
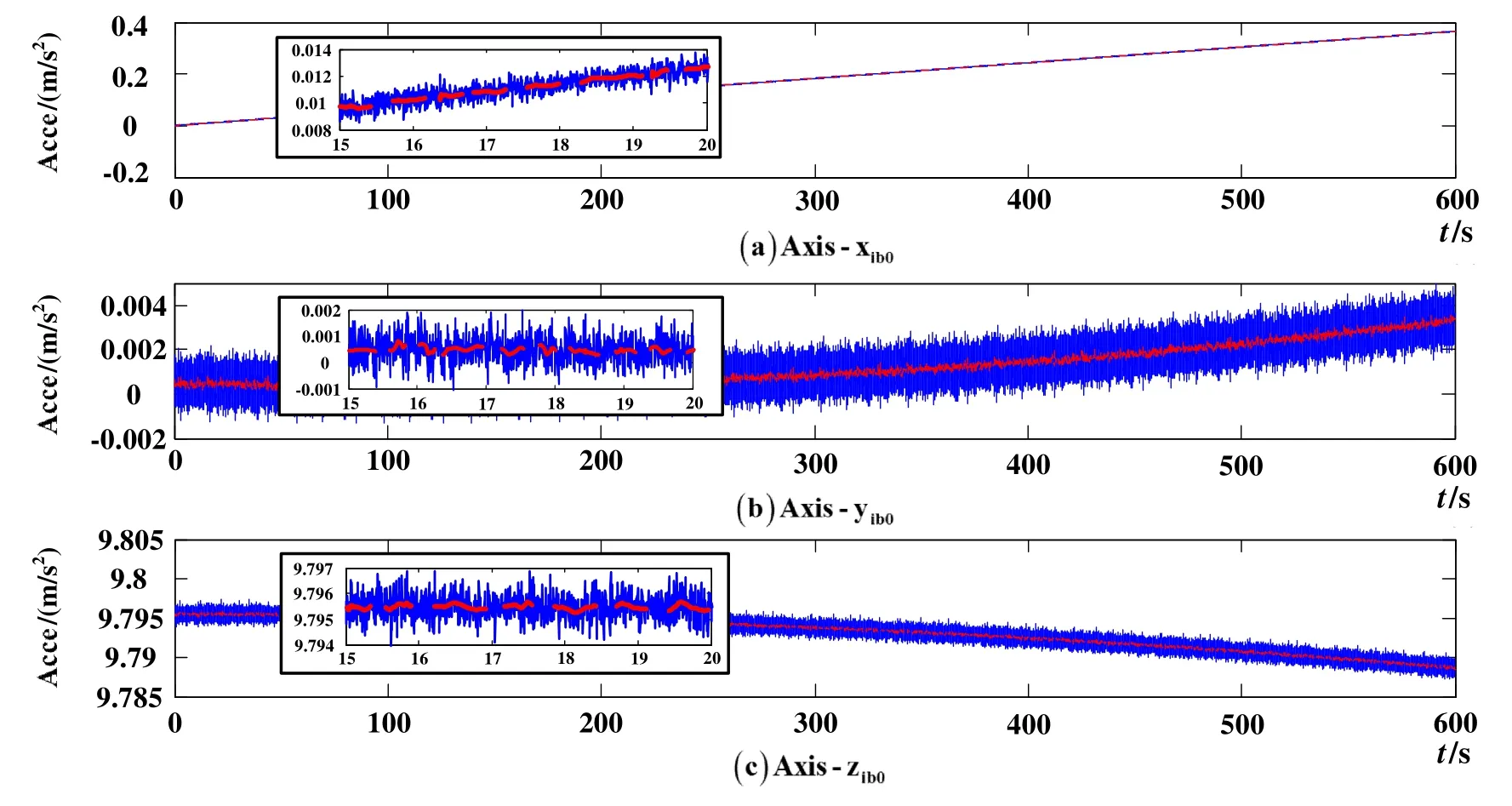
图5 惯性系中重力视运动投影值Fig.5 Projections of gravitational apparent motion in inertial frame
3 基于小波去噪的SINS自对准改进方法验证
3.1 仿真条件设置
为了验证基于小波去噪改进对准方案的有效性,进行晃动基座条件下的仿真验证。设有表4所示的两种运动情况,其中条件二同表1中条件二,仪表的常值误差与随机误差如表2所示。在表4中的第三种条件下,舰船以进行晃动,A、f、 η0与 θ0分别表示摇摆幅值、频率、初始相位及摇摆中心。摇摆参数如表5所示。

表4 仿真条件Tab.4 Simulation conditions
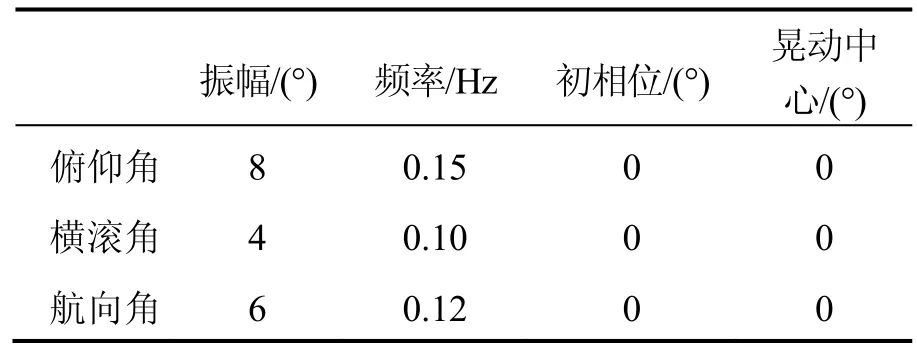
表5 摇摆参数Tab.5 Swing parameters
3.2 仿真结果及分析
图 6是改进方法在第二种条件下的对准误差曲线,在对准过程中,选择10 s、150 s、250 s三个时刻的重力视运动向量参与对准计算,对准在250 s结束,250 s之后进行纯惯性导航解算,解算时长为300 s。图7是改进方法在第三种条件下的对准误差曲线,在对准过程中,选择0 s、400 s、900 s三个时刻的重力视运动向量参与对准计算,对准在900 s结束,900 s之后进行纯惯性导航解算,解算时长为300 s。以对准结束后的捷联解算误差作为统计数据以评价对准结果,统计结果如表6所示。
由于纯惯性导航时间有限,仅为300 s,其解算误差、仪表误差的累积量有限,解算误差主要体现为初始对准误差。分析图6、图7中误差曲线以及表6中的统计结果,可以认为小波去噪有效地剔除了加速度计测量值中的随机噪声,基于小波去噪与三矢量的自对准算法可以有效完成未知纬度条件的 SINS初始对准,且对准精度接近于理论极限精度。

表6 改进方法的对准误差统计结果Tab.6 Statistics of alignment errors based on improved method

图6 改进方法在第二种对准条件下的对准误差曲线Fig.6 Curves of alignment errors based on the improved method under the second condition
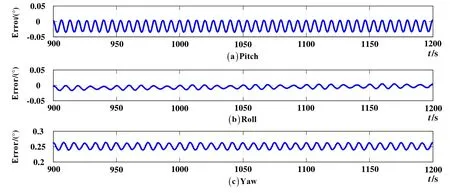
图7 改进方法在第三种对准条件下的对准误差曲线Fig.7 Curves of alignment errors based on the improved method under the third condition
4 结束语
本文提出并实现了一种未知纬度条件下,利用重力视运动实现SINS自对准的方法。该方法选择了惯性坐标系下三个不共线的重力视运动向量,通过矢量运算求取当前时刻导航系相对于初始时刻载体系的姿态矩阵,并进一步利用矩阵链式乘法完成初始对准。仿真结果表明,该方法的对准精度易受到重力视运动向量中的随机噪声的干扰,针对这一问题,本文选用了db4小波通过分层阈值的方法实现对重力视运动向量的预处理,将预处理过后的重力视运动向量运用于三矢量法的SINS自对准中,实现了对三矢量自对准算法的改进。仿真结果表明:db4小波可以有效地从重力视运动中去除高频噪声,利用消噪后的重力视运动向量参与对准计算,可以有效地完成未知纬度情况下的SINS的抗晃动自对准。
(References):
[1] Ali J, Fang Jiancheng. Alignment of strapdown inertial navigation system: A literature survey spanned over the last 14 years[D]. School of instrumentation Science and Optoelectronics Engineering, Beijing University of Aeronautics and Astronautics, Beijing, 2004: 100083.
[2] 张燕, 陈星阳. 导弹姿态矩阵更新算法推导和仿真验证[J]. 四川兵工学报, 2013, 34(8): 26-29. Zhang Yan, Chen Xing-yang. Derivation and simulation validating for attitude matrix updating algorithms for missiles[J]. Sichuan Ordnance Journal, 2013, 34(8): 26-29.
[3] 张剑慧, 秦永元, 龙瑞. 捷联惯导系统双矢量定姿方法研究[J]. 计算机测量与控制, 2010(11): 2634-2637. Zhang Jian-hui, Qin Yong-yuan, Long Rui. Studying on algorithm of double-vector attitude determination in SINS[J]. Computer Measurement & Control, 2010(11): 2634-2637.
[4] 经张俊, 程向红, 王宇. 捷联罗经的动基座自对准技术[J]. 中国惯性技术学报, 2009, 17(4): 408-412. Jing Zhang-jun, Cheng Xiang-hong, Wang Yu. Technology of strapdown gyrocompass self-alignment on moving bases[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 408-412.
[5] 杨功流, 王丽芬, 袁二凯, 等. 大方位失准角下舰载机快速传递对准技术[J]. 中国惯性技术学报, 2014, 22(1): 45-50. Yang Gong-liu, Wang Li-fen, Yuan Er-kai, et al. Rapid transfer alignment of lager misalignment angle for carrier aircrafts [J]. Journal of Chinese Inertial Technology, 2014, 22(1):45-50.
[6] Silva F O, Hemerly E M, Filho W C L. Influence of latitude in coarse self-alignment of strapdown inertial navigation systems[C]//2014 IEEE/ION Position, Location and Navigation Symposium. 2014: 1219-1226.
[7] 秦永元, 严恭敏, 顾冬晴, 等. 摇摆基座上基于信息的捷联惯导粗对准研究[J]. 西北工业大学学报, 2006, 23(5): 681-684. Qin Yong-yuan, Yan Gong-min, Gu Dong-qing, et al. A clever way of SINS coarse alignment despite rocking ship [J]. Journal of NorthWestern Polytechniacal University, 2006, 23(5): 681-684.
[8] 赵长山, 秦永元, 白亮. 基于双矢量定姿的摇摆基座粗对准算法分析与实验[J]. 中国惯性技术学报, 2009, 17(4): 436-440. Zhao Chang-shan, Qin Yong-yuan, Bai Liang. Analysis and test of swaying-based analytic coarse alignment[J]. Journal of Chinese Inertial Technology, 2009, 17(4): 436-440.
[9] Gaiffe T. From R&D brassboards to navigation grade FOG-based INS: the experience of Photonetics/Ixsea [C]//Optical Fiber Sensors Conference Technical Digest. IEEE, 2002: 1-4.
[10] Yan Gong-min, Weng Jun, Bai Liang, et al. Initial inmovement alignment and position determination based on inertial reference frame[J]. Systems Engineering and Electronics, 2011, 33(3): 618-621.
[11] Liu Xixiang, Xu Xiaosu, Zhao Yu, et al. An initial alignment method for strapdown gyrocompass based on gravitational apparent motion in inertial frame[J]. Measurement, 2014, 55: 593-604.
[12] Liu Xixiang, Liu Xianjun, Song Qing, et al. A novel self-alignment method for SINS based on three vectors of gravitational apparent motion in inertial frame[J]. Measurement, 2015, 62: 47-62.
[13] Liu Yiting, Xu Xiaosu, Liu Xixiang, et al. A self- alignment algorithm for SINS based on gravitational apparent motion and sensor data denoising[J]. Sensors, 2015, 15(5): 9827-9853.
[14] 胡礼勇, 李钊, 李建军, 等. 基于小波的惯导系统初始对准方法研究[J]. 无线电工程, 2011, 41(4): 31-33. Hu Li-yong, Li Zhao, Li Jian-jun, et al. Initial coarse alignment technique based on wavelet for inertial navigation system[J]. Journal of Wireless Engineering, 2011, 41(4): 31-33.
[15] 赵春莲, 翁浚, 严恭敏, 等. 小波域阈值滤波在基于惯性系对准中的应用[J]. 测控技术, 2014, 33(2): 32-35. Zhao Chun-lian, Weng Jun, Yan Gong-min, et al. Application of wavelet domain threshold filtering in alignment based on inertial frame[J]. Journal of Measurement and Control Technology, 2014, 33(2): 32-35.
[16] Ilyas M, Yang Y, Zhang R. SINS initial alignment using wavelet de-noising method for aircraft navigation[C]// 2012 10th World Congress on Intelligent Control and Automation. IEEE, 2012: 3921-3926.
[17] Huang B, Sun P J, Wang X M. The denoising method based on wavelet transform in signal dynamic detection [C]//Advanced Materials Research. 2014, 889: 766-769.
Self-alignment algorithm without latitude for SINS based on gravitational apparent motion and wavelet denoising
LIU Xi-xiang1,2, YANG Yan1,2, HUANG Yong-jiang1,2, SONG Qing1,2
(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University, Nanjing 210096, China; 2. School of Instrument Science & Engineering, Southeast University, Nanjing 210096, China)
Double-vector attitude determination algorithm in inertial frame takes two gravitational apparent motion vectors as non-collinear vectors. Although this method solve the traditional algorithm’s problem that the information is susceptible to angular motion disturbance on swinging base, it still needs accurate latitude information to participate in alignment calculation. Aiming to fulfill the alignment for strapdown inertial navigation system without aided latitude information, a self-alignment method with three gravitational apparent motion vectors is designed. In this method, the alignment problem is attributed to solving the attitude matrix between current navigation frame and initial body frame and is solved with vector operation. Simulation results indicate that those random noises in the accelerator will be projected in gravitation apparent motion vectors and decrease the alignment accuracy, and even cause alignment failure when with large noise. For denoising, the daubechies (db4) wavelet is introduced to decompose gravitational apparent motions with 5 layers, and three denoised apparent motion vectors are selected to participate in the alignment. Simulation results indicate that the db4 owns excellent denoising effects and the alignment method with three apparent motion vectors and db4 in inertial frame can fulfill the alignment without aided latitude information.
strapdown inertial navigation system; initial alignment; gravitational apparent motion; wavelet denosing; tri-vector attitude determination
U666.1
:A
2016-02-04;
:2016-05-20
自然科学基金(61273056)
刘锡祥(1976—),男,博士,教授,研究方向为惯性导航与组合导航技术。E-mail: scliuseu@163.com
1005-6734(2016)03-0306-08
10.13695/j.cnki.12-1222/o3.2016.03.006
