基于非相关多线性主成分分析的人脸识别算法

杨凌云，秦　岸

( 1．安徽师范大学物理与电子信息学院，安徽芜湖241000; 2．重庆市公安局巴南区分局科技信息化科，重庆400055)



基于非相关多线性主成分分析的人脸识别算法

杨凌云1，秦岸2

( 1．安徽师范大学物理与电子信息学院，安徽芜湖241000; 2．重庆市公安局巴南区分局科技信息化科，重庆400055)

摘要:针对在人脸识别算法中，维数的增加往往会给算法的运算带来沉重负担的问题，提出了一种新的基于非相关多线性主成分分析( UMPCA)和线性判别分析( LDA)的人脸识别算法，算法在保证在降维的时候保留尽可能多的内部结构信息。UMPCA通过一张量至向量的过程，可直接获取原张量数据的绝大部分非相关特征，提取的特征再通过经典算法LDA处理。利用AT&T人脸数据库对该算法进行了实验，实验数据分析显示该算法优于其他同类算法。

关键词:张量;非相关多线性主成分分析( UMPCA) ;线性判别分析( LDA) ;特征提取

Face Recognition Algorithms Based on Uncorrelated Multilinear PCA

0引言

人脸识别是子空间分析中一个重要的应用领域。在过去的十几年中，出现了很多用于人脸识别的算法，其中应用最广泛最经典的是主成分分析( PCA)[2]和线性判别分析( LDA)[3]算法。当输入数据为张量时，经典处理算法总是将张量数据转换为矢量数据，但这一转换会带来很高的计算量和沉重的存储负担[4]。除了计算量和存储问题外，该转换还会破坏原数据的内部结构和相关性。因此，一些学者们提出了多线性算法，这类算法可对高阶张量数据直接运算，而无需将其转化被向量，如( 2D)2PCA[5]和( 2D)2LDA[6]．( 2D)2PCA和( 2D)2LDA算法在处理二阶张量数据，如人脸识别中，取得了良好的效果。然而，他们只针对二阶张量，对于更高阶次的数据则无能为力。

最近，对于高阶数据的信号处理方法，也有了新的进展。在文献[7]中，一种利用k模交替优化的方法进行优化的新算法多线性判别算法( MDA)被提出。同传统PCA原理类似，多线性主成分分析( MPCA)通过求取张量各阶次的展开矩阵的最大特征值对应的特征向量组成的转换矩阵，将一个高维张量线性转换为同阶次低维张量。该算法在多次实验中验证了其有效性和优越性。在文献[9]中，将MPCA和MDA两个都直接用于张量的多线性算法组成起来，经MPCA提取的特征值再通过MDA进行处理，取得了更好的效果。除了多线性算法外，非相关多线性算法近年来也颇受关注。PCA的非相关多线性扩展采用了PCA算法的一个重要性质，即经过PCA提取的特征值之间是非相关的。非相关的参量在很多识别任务中扮演重要角色，因为非相关的性质使参量之间的冗余最小，使各参量之间线性独立[10]。无监督张量特征提取算法非相关多线性主成分分析( UMPCA)通过一张量至向量的映射( TVP)[11]，使输入张量直接转换为向量。TVP即指一个向量通过P个由张量到数的映射，获取一个P ×1的向量的映射过程。

1 UMPCA和LDA

作为PCA的一种多线性扩展，MPCA不仅使提取的特征值方差最大化，并且采用了零相关的约束条件，从而通过与经典PCA相似的方法提取了非相关的特征值[12]。受Fisherface算法的启发，首先采用UMPCA对张量数据直接进行特征提取，对提取后的特征数据输入到LDA算法中。最后，采用最近邻分类器来对经过LDA输出的特征数据进行分类。

1．1 UMPCA

文献[13]对UMPCA算法进行了详细的介绍。一组M个张量{x1，x2，．．．，xM}，各张量xm∈RI1* I2*．．．* IN，其中In表示第n模的维数( n = 1，2，…，N)，*表示克罗内克积。UMPCA算法的目标是计算出由P个EMP {∈RIn* 1，n = 1，．．．组成的TVP，使原张量空间映射到一矢量空间Rn( with

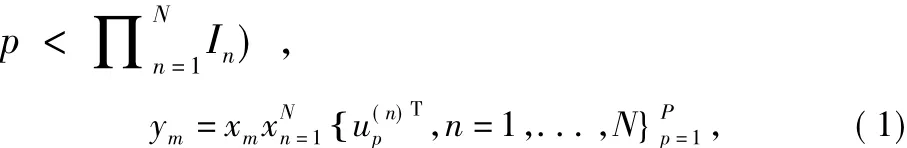
式中，δpq为克罗内克δ

步骤1:使SyT1最大化，计算第1个EMP，n = 1，．．．;

1．2 LDA

经典有监督算法LDA和UMPCA相组合用于人脸识别。一组分属于c类的M个样本，类内矩阵定义为:

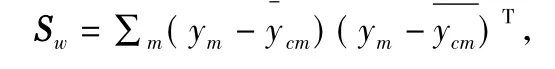
和

类间矩阵定义为:

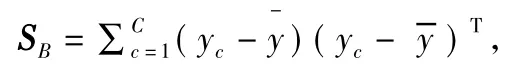
和

优化矩阵V定义为:

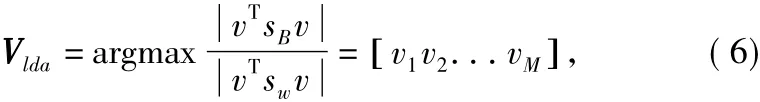
其中，{ vm，m = 1，．．．M}对应于SB与Sw比值的最大特征值的特征向量，表示为: sBvm=λmswvm。LDA输出值zm为: zm=。

2实验验证

AT&T人脸数据库[14]包含有400张112x92的人脸灰度图像，他们分属于40个类，每类10张。图1给出了该数据库2个不同人脸的几张图片，它们之间各不相同，具有不同特点。

在图1的实验中，每类人脸中随机选取5张用于训练，剩下的5张用于验证。图2给出了对于提取不同特征维数值P时，PCA + LDA、2DPCA + 2DLDA、MPCA + LDA、UMPCA和UMPCA + LDA算法的识别率。

由图2可看出，在所有不同P的取值中，UMP-CA + LDA都取得了最好的识别效果，并且在P =10时达到了饱和。这是因为经过UMPCA降维后，信息量被高度集中，当P值大于10时，对于识别的影响不大。所以在接下来的实验中，只讨论p = 1，．．．，10时的试验情况。

图1 AT&T人脸数据库中的人脸图像

图2每类5张图像用于训练的人脸识别率

在表1的实验中，每一类随机选取L个图像用来训练。表1列出了P = 1，3，6，9，L = 2，4，6，时的识别率，其中算法中最高的识别率用黑体标出。可观察出，UMPCA + LDA在所有比较的算法中取得了最好的效果。

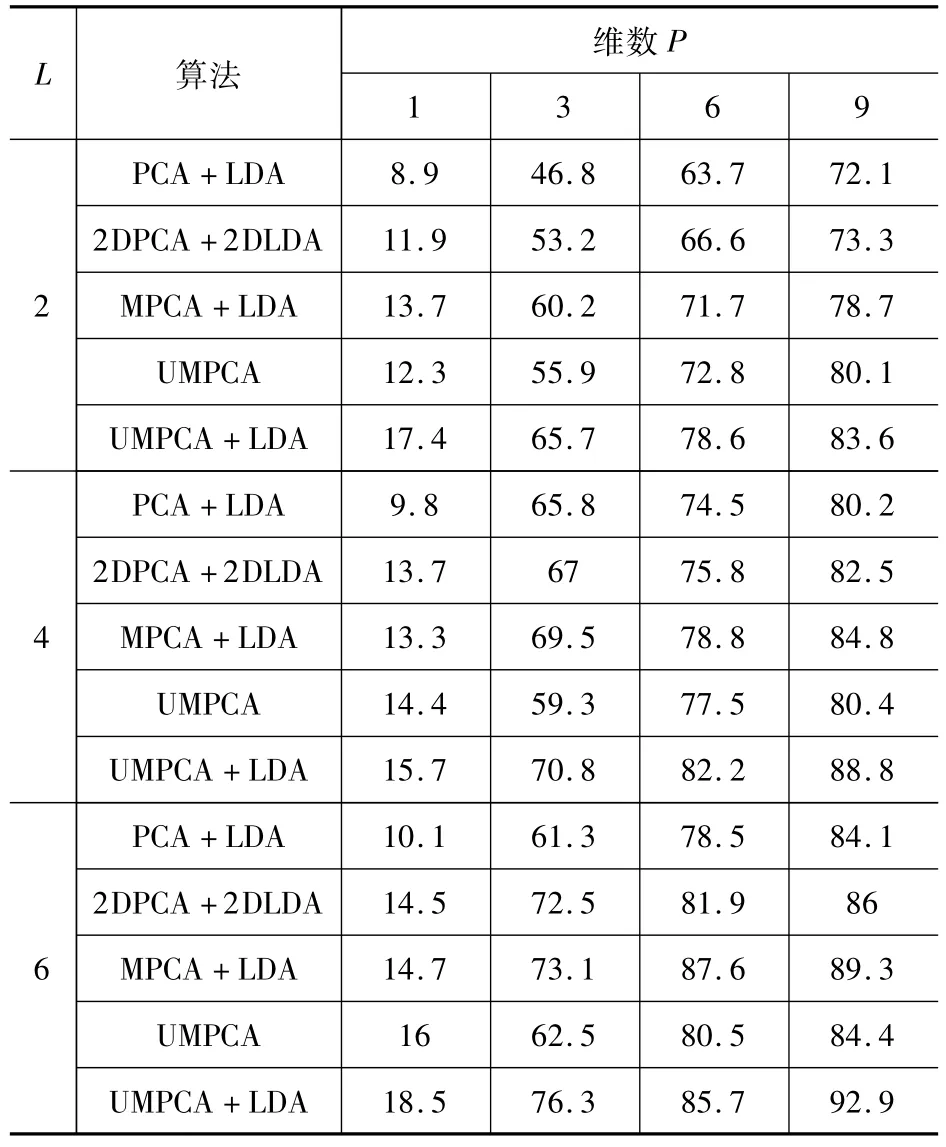
表1对应不同图像个数L和维数P的识别率

3结束语

采用UMPCA +LDA算法可以提高人脸识别的效果。UMPCA算法可直接从张量数据中提取非相关特征值，再采用LDA进一步提交识别率。在人脸数据库的实验表明，从其他PCA同LDA相组合的算法相比，如PCA +LDA、2DPCA +2DLDA、MPCA + LDA and UMPCA、tUMPCA + LDA取得了最好的识别效果，该算法适用于人脸等高阶张量的降维识别应用。

参考文献

[1]Law M H C，Jain A K．Incremental nonlinear dimensionality reduction by manifold learning[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，2006( 28) : 377-391．

[2]Belhumeur P，Hespanha J，Kriegman D．Eigenfacesvs．Fisherfaces: Recognition using class specific linearprojection[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，1997( 19) :711-720．

[3]Pentland Turk M．Face Recognition Using Eigenfaces [C]/ /the IEEE Conf．Computer Vision and Pattern Recognition，1991:586-590．

[4]He X，Yan S，Hu Y．Learning a locality preserving subspace for visual recognition[C]/ / Proc．9th IEEE Int．Conf．Computer Vision，2003: 385-392．

[5]Zhang D，Zhou Z．( 2d)2pca: 2-directional 2-dimensional Pca for Efficient Face Representation and Recognition [J]．Neurocomputing，2005( 29) : 224-231．

[6]Noushath S，Kumar G H. Shivakumara P．( 2d)2lda: An Efficient Approach for Face Recognition[J]．Pattern Recognition，2006( 39) : 1396-1400．

[7]Yan S，Xu D，Yang Q，et al．Multilinear Discriminant Analysis for Face Recognition[J]．IEEE Transactions on Image Processing，2007( 16) :212-220．

[8]Plataniotis H，Lu K．Venets -anopoulos A，MPCA: Multilinear Principal Component Analysis of Tensor Objects [J]．IEEE Transactions on Neural Networks，2008( 19) : 18-39．

[9]Sun M，Liu X，Wang S．Human Action Recognition Using Tensor Principal Component Analysis[J]．Journal of Computational Information Systems，2011 ( 8 ) : 10053 -10061．

[10]Ye J，Janarda R，Li Q，et al．Feature Reduction Via Generalized Uncorrelated Linear Discriminant Analysis[J]．IEEE Trans．Knowl．Data Eng，2006( 18) : 1312-1322．

[11]Plataniotis H，Lu K，Venetsanopoulos A．A survey of Multilinear Subspace Learning for Tensor Data[J]．Pattern Recognition，2011( 44) : 1540-1551．

[12]Lu H，Plataniotis K，Venetsanopoulos A．Uncorrelated multilinear Principal Component Analysis for Unsupervised Multilinear Subspace Learning[J]．IEEE Transactions on Neural Networks，2009( 20) : 1820-1836．

[13]Plataniotis H，Lu K，Venetsanopoulos A．Uncorrelated Multilinear Principal Component Analysis Through Successive Variance Maximization[C]/ /Proc．25th IEEE Int．Conf．Machine Learning，2008: 616-623．

[14]AT&T TheDatabase of Faces[EB/OL]．Online available: http: / /www．cl．cam．ac．uk/research/dtg/ attarchive/ facedatabase．html．

[15]Plataniotis H，Lu K，Venetsanopoulos A．Gait recognition through MPCA plus LDA[C]/ /Proc．Biometrics Symposium，2006:1-6．

引用格式:江会娟，章劲松．GEO卫星波束指向地面轨迹的计算与应用[J]．无线电通信技术，2016，42( 1) : 76-78，85．

YANG Ling-yun1，QIN An2
( 1．College of Physics and Electronic Information，Anhui Normal University，Wuhu Anhui 241000，China;
2．Science&Technology Informatization Section，Banan Branch，Chongqing Public Security Bureau，Chongqing 400055，China)

Abstract:In face recognition algorithms，the increase of feather dimensionality has always over-burdened the algorithm operation，so a new face recognition algorithm based on UMPCA and LDA is proposed．While the algorithm reduces the dimensionality，it remains the inner structure information as much as possible．UMPCA seeks a tensor-to-vector projection that captures most of the variation in the original tensorial input while obtaining uncorrelated features through successive variance maximization．A subset of features extracted is processed by classical LDA to find the best subspaces．Finally，the comprehensive experiments are provided on AT&T databases and the experiment results show its performance over other PCA plus LDA based algorithms．

Key words:tensor object; uncorrelated multilinear principal component analysis; linear discriminant analysis;feature extraction

doi:book=76,ebook=810．3969/j．issn．1003-3114．2016．01．20

作者简介:杨凌云( 1983―)，女，讲师，通信工程专业，主要研究方向:信号处理。秦岸( 1980―)，男，工程师，交通信息工程专业，主要研究方向:交通信控。

收稿日期:2015-07-15

中图分类号:TP391．41

文献标识码:A

文章编号:1003-3114( 2016) 01-73-3