一种HFDL信号Turbo均衡器设计与实现

佟长凯，应文威，李成军，郭凯丰

( 1．中国人民解放军91635部队，北京102200; 2．哈尔滨工程大学，黑龙江哈尔滨150000)



一种HFDL信号Turbo均衡器设计与实现

佟长凯1，应文威1，李成军1，郭凯丰2

( 1．中国人民解放军91635部队，北京102200; 2．哈尔滨工程大学，黑龙江哈尔滨150000)

摘要:为了提高恶劣条件下HFDL信号接收性能，设计了针对HFDL信号特征的Turbo均衡器。HFDL-Turbo均衡器充分挖掘了信号特征，并优化了前端均衡器和译码器结构。算法对多相信号进行单比特软值映射处理，避免交织之前的硬映射，并对重复编码信号采用矢量合成技术以充分利用编码增益。在未知信道条件下，完成了从信道估计、均衡和译码的全过程仿真，仿真结果表明设计的HFDL-Turbo均衡器在存在码间串扰条件下仍具有优异的均衡、译码性能。

关键词:HFDL信号; Turbo均衡; MMSE算法

0引言

High-Frequency Data Link ( HFDL)系统[1]是ARINC公司研制的民航空地短波通信系统。它利用短波信道发送飞机位置、航班号、地址码和地面站位置等信息，并通过其覆盖半径超过3 000 km的全球15个地面站实现对全球民航飞机的监控。目前该系统在各国航空系统中获得了广泛的应用，是航空公司远距离识别监控飞机飞行安全及数据传输的重要手段。但是由于系统工作在短波波段，频带范围为2～30 M，其传播信道受到多径、多普勒频移、脉冲噪声和信道时变等诸多因素干扰，这些不利因素严重影响了HFDL信号的接收解调性能。为了提高接收解调性能，一般接收机都采用均衡技术对信号进行预先处理。常用的均衡器有线性均衡器、判决反馈均衡器及分数间隔均衡器。但是由于短波信道时常出现严重的码间串扰，常规的均衡器处理此类干扰很难取得良好的均衡效果。Turbo均衡是依据Turbo码原理改进而来的一种均衡器，通过迭代运算可以逼近AWGN信道条件下信号传播性能。本文根据HFDL信号特点，设计HFDL-Turbo均衡器，挖掘信号特征潜力，提升算法性能，同时优化算法，降低运算复杂度。

1 HFDL信号

HFDL工作在短波波段，采用TDMA方式进行复用，射频采用上边带调制( USB)将基带信号调制到载波。基带采用MPSK( BPSK、QPSK和8PSK)调制方式，符号速率为1 800 Bd，基带信号载波频率1 440 Hz。系统根据信道质量自适应选择数据传输速率( 300 bps、600 bps、1 200 bps和1 800 bps)，信息数据经过( 2，1，7)卷积码编码后，送入交织器，交织后的数据经符号映射、加扰再与Prekey、Preamble及训练序列进行拼接，其结构如图1所示。最后经过调制、成形滤波放大发送到空中[1]。HFDL信号采用自适应速率调节技术，信号传播过程中自行根据信道条件调整编码方式和调制样式这就更增加了其解调难度。

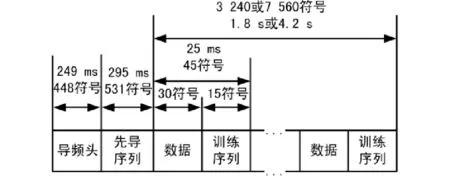
图1 HFDL信号结构

2 HFDL信号Turbo均衡器

2．1 Turbo均衡器结构及基本原理

HFDL工作在短波波段，又属于窄带突发信号，因此采用Watterson模型[2]即可对其信道进行较准确的仿真及分析。根据Watterson模型，其信道冲激响应可表示为:

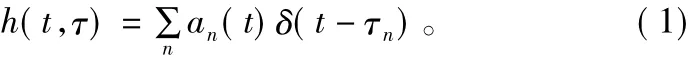
由式( 1)可以看出，信号传输信道可以看成一个编码率为1的卷积编码器。假设发送信号采用卷积码进行前向纠错，那么在接收端接收信号相当于一个串联Turbo码信号。通过在接收端对接收信号进行Turbo译码就可实现抵消码间串扰及卷积码前向纠错功能[3]。这种将信道冲激响应视为卷积编码，在接收端将均衡与译码联合实现的方法被称为Turbo均衡[4]，其基本结构如图2所示。

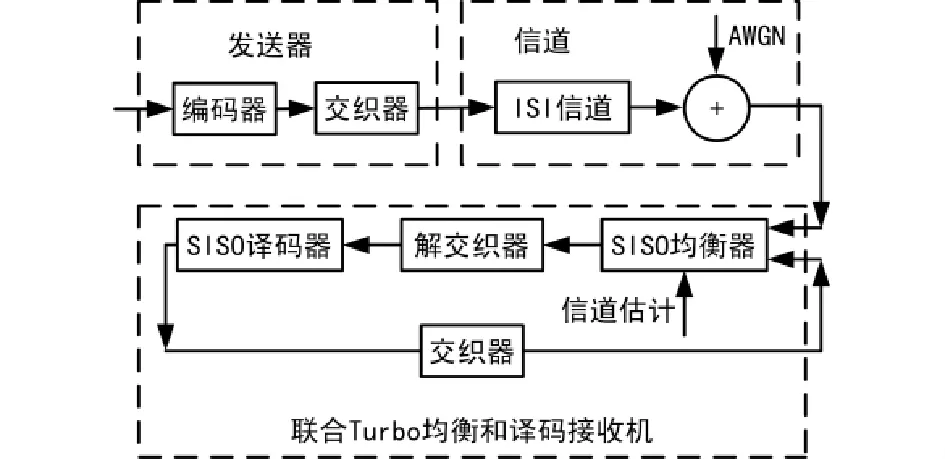
图2 Turbo均衡器结构

Turbo均衡最经典的算法是MAP算法，又由MAP算法衍生出简化算法LOG-MAP算法。这2种算法是性能最优的2种均衡算法，但是算法运算量较大，虽然LOG-MAP算法对MAP算法进行了简化处理，但依然包含大量的对数运算。同时这2种算法能够获得优异性能的前提是能够准确估计出信道冲激响应，一旦出现信道冲激响应误差较大时，整个均衡器性能将急剧下降。

另一种均衡算法是基于MMSE准则的线性均衡算法[5-8]。这种算法是由传统线性均衡器改进得到的，具有算法复杂度适中，性能稳定的特点。

2．2 HFDL-Turbo均衡器均衡算法设计

综合考虑性能和运算复杂度，在构造HFDLTurbo均衡器时采用基于MMSE准则的线性均衡算法，同时根据信号特点，在不降低性能的前提下改进算法，降低运算量。

假设发送序列为xn，接收序列为yn，根据Watterson模型，yn可表述为:

式中，wn为噪声序列; H为由信道冲激响应构成的N×( N + M-1)矩阵，M为信道冲激响应长度，线性滤波器阶数N，N = N1+ N2+ 1，N1为估计滤波器中非因果响应长度，N2为因果响应长度。根据最小均方误差准则，最小化代价函数MSE = E[|-x |2]后可得到估计值:

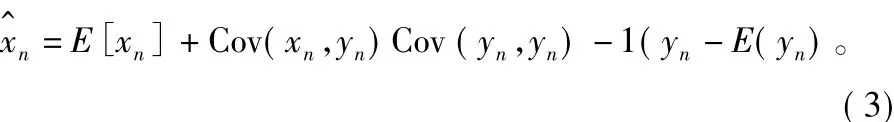
由于信号通过ISI信道，所以式( 3)可写为:

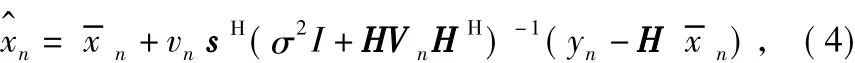
式中，

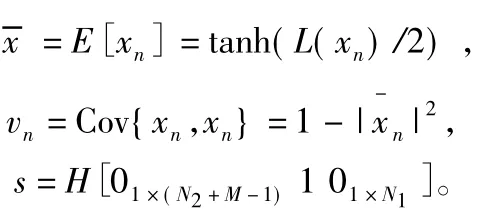
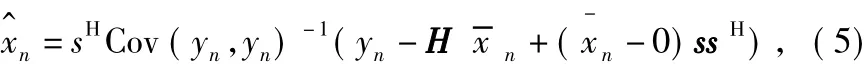
均衡器输出为:

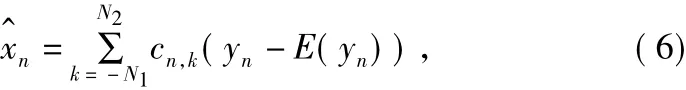
式中，E( yn) =∑hkn-k，滤波器系数向量可写

为cn=[c，N2c，N2-1…c，-N1]T，由此可得:

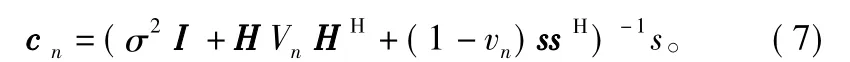
因此最后均衡器估计值为:

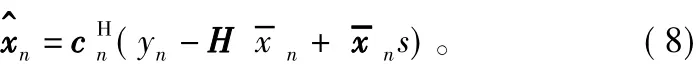
在MMSE准则下，x^n服从N～(μn，x，σ2n，x)。

式中，

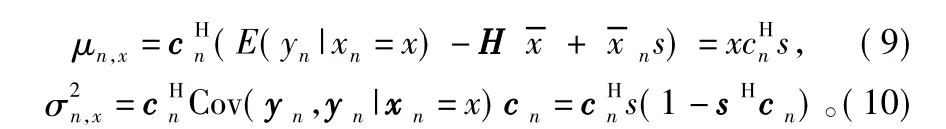
因此，均衡器输出软信息为:

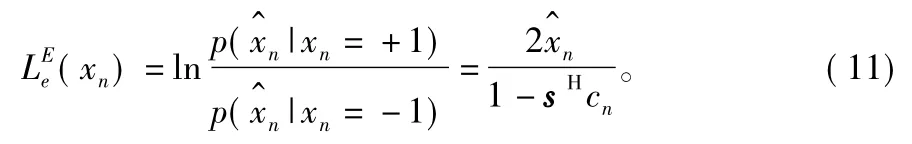
式( 11)中外部信息的计算采用的是估计值而不是观测值，即在经过均衡后对均衡后数据进行处理来得到外部信息。均衡器输出的信息序列的对数似然比经过解交织后即可作为译码器的先验信息，而译码器输入的信息序列对数似然比经过交织后输入的均衡器中用于计算均衡器输入数据的E[xn]、Cov{ xn，xn}。HFDL-Turbo均衡器流程如图3所示。

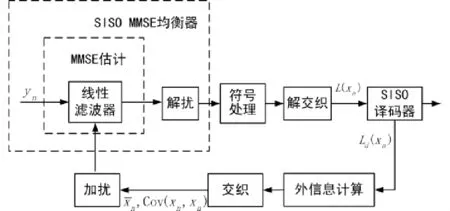
图3 HFDL-Turbo均衡器流程图

由式( 7)可以看出，在每个符号软信息的计算过程中都需要求逆运算，而求逆运算将会使整个算法的运算量迅速增加，这是不希望看到的，为此本文根据HFDL信号特点对算法进行了改进。

由第1节知道，HFDL信号的数据段中，每30个数据符号即插入有15个符号的训练序列，这45个符号只持续45/1 800 s。如此短的时间内可认为其传输信道为恒参信道。

通过式( 7)可知，算法中正是因为x-n是时变参数，这就造成式( 7)中每一符号的计算中都包含求逆运算，简化算法是用每一个训练周期内xn的时间均值代替，这样每30个数据符号才需一次求逆运算，而不是每个比特都需要求逆运算。这样式( 7)可写为:

这种设计避免了MMSE均衡算法在计算每个符号的软信息时都进行求逆运算而只需一个训练周期进行一次求逆运算。

从算法的推导过程可以看出，均衡器在运行过程中输出为符号信息，而译码器输入为比特信息，为此在进行译码运算前，还必须将接收到的符号信息映射为比特信息。HFDL信号采用的3种映射方式( BPSK、QPSK和8PSK)中，只有BPSK信号可以直接通过接收符号获取概率信号，而QPSK、8PSK信号每个符号都包含数个比特[9，10]，因此需对符号进行比特映射，提取出每个比特的概率信息，在进行后续的计算。下文单对QPSK和8PSK进行符号映射处理。

QPSK第1比特的0与1关于135°虚线对称，因此第1比特软值为:

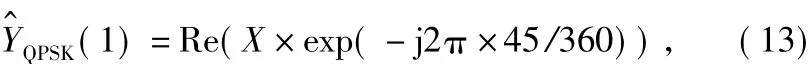
即将接收符号的坐标顺时针旋转45°并取实部。同理，第2比特软值为:

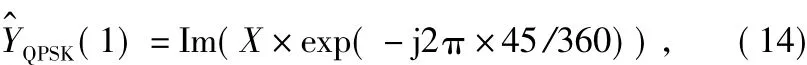
即将接收符号的坐标逆时针旋转45°并取实部。

在工程实现时，可以直接将观测点到分界线的距离作为软值输入，从理论上是同上法等价的。在计算距离时第1比特软值为观测值实部减去虚部除以，同理第2比特为实部与虚部的和除以。

8PSK第1比特的0与1关于157．5°虚线对称，因此第1比特软值为:

即将接收符号的坐标逆时针旋转22．5°并取虚部。

第2比特软值输出为:

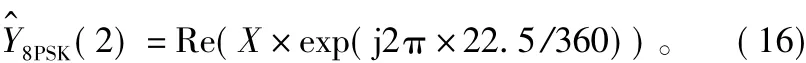
对于第3比特，发现难以像之前分析那样用一条虚线在复平面上进行划分，也就是比特0与比特1之间的最大距离要小于第1比特和第2比特的最大距离，即按当前的格雷编码规则，第3比特的最大可信度会减小。因此，可先对解调星座图进行适当调整，即先关于y轴折叠，再关于x轴折叠，这时比特0与1关于45°虚线对称。再逆时针旋转45°，可使比特0与1关于y轴重叠。

根据上述分析，具体计算步骤如下:

Y1= X×exp( j2π×22．5/360)，

Y2= Abs( Re( Y1) )，

Y3= Abs( Im( Y1) )，

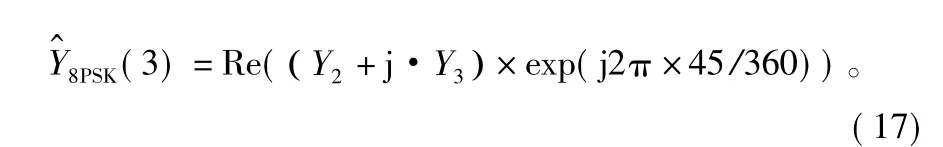
2．3 HFDL-Turbo均衡器译码算法设计

由图1可知，Turbo均衡器不光包含前端均衡器还包括后端译码器，译码器的选择和设计同样影响着整个均衡器的性能。SISO译码器中，性能最好的就是MAP算法，但这种算法运算量太大，所以采用其简化算法LOG-MAP算法。LOG-MAP算法在性能上同MAP算法相似，但由于是在对数条件下进行的，因此大量的乘法运算可变为加法运算降低了算法的运算复杂度。虽然算法性能优异，但若要将其应用到HFDL-Turbo均衡器中，还需对算法进行改进。这主要是因为在信道条件较差时，HFDL会采用一种特殊的编码方式，即在卷积码编码后采用重复编码的技术提高抗干扰能力。由表1可以看到，相邻重复比特仅采用一个比特即能达到解译的目的，但从信息论的角度来说，充分挖掘利用该重复信息，可获得额外的解译能力。为此本文在译码过程中，将2个重复信号进行矢量合成，以此提高其译码性能。

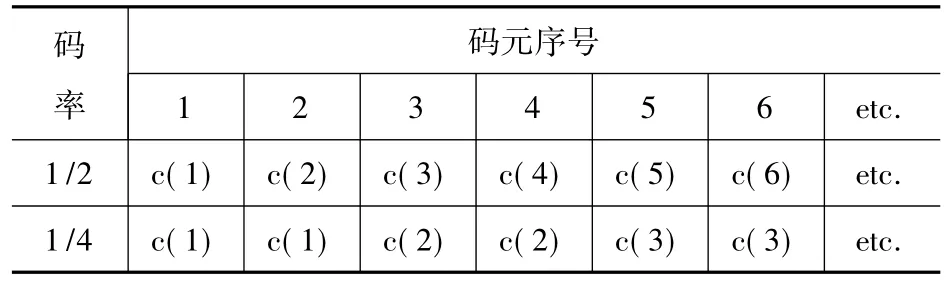
表1编码关系表

3性能仿真

仿真采用2种典型的存在深度衰落信道[11]，其冲激响应分别为:

信道A:[0．407 0．815 0．407]

信道B:[0．227 0．460 0．688 0．460 0．227]

仿真信号按照实际接收的600 bps的HFDL信号构造，先通过RLS算法估计信道冲激响应[12]。均衡器迭代条件设置为5次。作为对比组同时采用DFE均衡，DFE前馈滤波器阶数及后馈滤波器阶数均为15，训练模式采用遗忘因子为0．999 95的RLS算法，均衡模式采用步进0．000 01的LMS算法。值得一提的是，由于Turbo均衡是均衡和译码同时实现的，所以对DFE均衡后的信号进行了维特比译码，仿真试验的误码率结果都为译码后的误码率。A信道条件下HFDL-Turbo均衡器与DFE的误码率如图4所示。

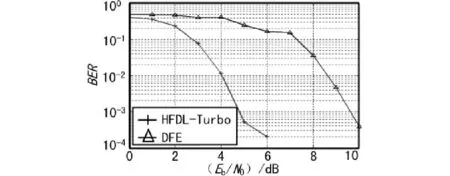
图4 HFDL-Turbo均衡器与DFE的误码率( A信道条件下)

从图4可以看出，HFDL-Turbo均衡器较传统均衡器性能有较大提升，当信噪比大于3 dB时，比DFE可以多获得4 dB的性能增益，当Eb/N0≥6时，即可实现近似无差错的传输了，而此时DFE误码率还非常高。B信道条件下Turbo-HFDL与DFE的误码率如图5所示。

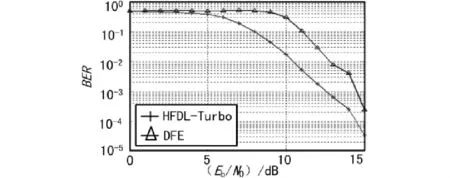
图5 HFDL-Turbo均衡器与DFE的误码率( B信道条件下)

从图5中不难看出，有类似图4的仿真结果。但由于B信道衰落条件更为恶劣，因此2种均衡器的性能都较A信道条件下有所降低，但HFDL-Turbo均衡器较DFE性能更为优异，可比DFE多获得2 dB的增益。

对于HFDL信号1 200 bps、1 800 bps的数据传输速率的仿真类似于600 bps，只不过在每比特信息的提取上及信噪比和Eb/N0的关系上有所不同，本文就不在赘述。但是300 bps的数据传输速率同其他传输速率上在编码方式上有所不同，采用了卷积码重复编码技术，因此本文进行了单独仿真。

当在信道A条件下，对采用软信息矢量合成技术和未进行矢量合成的HFDL-Turbo均衡器进行仿真比较，仿真结果如图6所示。

从图6中可以看出，矢量合成后均衡器性能得到了提升，特别是当Eb/N0≥4后，采用矢量合成的HFDL-Turbo均衡器较未采用的HFDL-Turbo均衡器性能优势逐渐增大。

图6采用矢量合成及未采用矢量合成的Turbo-HFDL均衡器误码率( A信道条件下)

4结束语

短波HFDL信号的均衡技术一直以来都是短波信号处理领域的一项挑战。针对HFDL信号设计了HFDL-Turbo均衡器，并根据HFDL信号特点进行了算法优化。通过同传统均衡器进行仿真比较，表明HFDL-Turbo均衡器在性能上有较大提升。实时Turbo均衡技术以往受限于运算复杂度等因素，在硬件平台上实现困难，但随着目前数字软硬件水平的不断发展，硬件平台已不再成为约束Turbo均衡技术实现的瓶颈，本文所设计的HFDL-Turbo均衡器也易于在现有计算机通用硬件平台上实时实现，因此具有较高的实用价值。[1]Airlines Electronic Eengineer committee．HF data Link protocols arinc specification 635-4，aeronautical radio [S]．

参考文献

[2]王金龙．短波数字通信研究与实践[M]．北京:科学出版社，2013:15-20．

[3]罗显志，高东博．一种导航信号用Turbo码编译码FPGA实现[J]．无线电工程，2015，45( 3) :54-57．

[4]Koetter R，Singer A C，Tuchler M．Turbo Equalization [J]．IEEE，2004:67-80．

[5]Tüchler M，Koetter R，Singer A C．Turbo Equalization: Principles and New Results[J]．IEEE，2002:754-767．

[6]Benammar B，Thomas N，Poulliat C．On Linear MMSE Based Turbo-Equalization of None linear Volterra Channels[J]．IEEE，2013:4703-4707．

[7]Oletu G，Rapajic P．Modified Iterative Decision Feedback Equalization for Communication Systems[J]．IEEE，2013:600-604．

[8]Tü chler M，Koetter R，Singer A C．Minimum Mean Squared Error Equalization Using a Priori Information [J]．IEEE，2002:643-683．

[9]ZHANG Jun，SHI Kai-yuan，PENG Hua．On the Optimality of MAP Bit Detection of Coded M-PSK Signals[J]．IEEE，2008:543-548．

[10]崔霞霞，江会娟，明刚．一种8PSK、16APSK与32APSK软解映射的实现技术[J]．无线电工程，2011，41( 4) : 45-48．

[11]LI Qiang，Teh K C，Li K H．Low-complexity Iterative Receivers with Adaptive Channel Estimation Algorithm over High Frequency Waveform Channels[J]．IEEE，2012: 2432-2435．

[12]Proakis G J．Digital Communications ( 5th Edition)[M]．

American: McGraw Hill Higher Education，2009．

Design and Implementation of a HFDL -TURBO Equalizer

TONG Chang-kai1，YING Wen-wei1，LI Cheng-jun1，GUO Kai-feng2

( 1．Unit 91635，PLA，Beijing 102200，China; 2．Harbin Engineering University，Harbin 150000，China)

Abstract:In order to improve the HFDL signal receiving performance under severe conditions，the equalizer is designed in view of HFDL signal characteristics．The HFDL-Turbo equalizer fully uses the signal characteristics，and optimizes the structure of the front end equalizer and the decoder．In the algorithm，the MPSK signal is demodulated by single bit soft valve，avoiding hard mapping before interleaving，and the vector synthesis technology is used for repetitive coding signal to fully utilize the coding gain．Finally，under the unknown channel condition，the overall process simulation is implemented，including channel estimation，equalization and decoding．The simulation results show that the equalizer has better equalization and decoding performance under the ISI channel．

Key words:HFDL signal; Turbo equalization;MMSE algorithm

作者简介:佟长凯( 1986—)，男，硕士研究生，主要研究方向:信号处理。应文威( 1987—)，男，博士，工程师。主要研究方向:水声通信。

收稿日期:2015-09-28

中图分类号:TN911

文献标识码:A

文章编号:1003-3114( 2016) 01-94-5