需求依赖库存水平的非一体化供应链IRP研究

刘　俊,　刘桂庆

(合肥工业大学 数学学院,安徽 合肥　230009)



需求依赖库存水平的非一体化供应链IRP研究

刘俊,刘桂庆

(合肥工业大学 数学学院,安徽 合肥230009)

摘要:文章针对单一供应商和多零售商组成的非一体化供应链,研究了零售商市场需求依赖于其当前库存水平情形下的库存路径问题(inventory routing problem,IRP)；在分散式系统下,建立了供需双方的利润模型,给出了改进的最邻近算法,降低了运输费用,提高了供应链的整体利润,再通过价格策略实现了供应商和各零售商多赢,促进了供应链的协调；并给出算例对模型进行了仿真计算与分析。

关键词:库存影响需求;非一体化供应链;库存路径问题;供应链协调;价格策略

0引言

库存路径问题 (inventory routing problem,IRP)旨在对库存和路径2个方面的问题进行联合考虑来提高供应链的整体利润。自IRP提出以来,IRP 受到研究者的广泛关注,并迅速成为供应链管理中的研究热点之一[1]。文献[2]研究了非一体化供应链下的IRP,提出了一种价格协调策略。在零售商市场需求为随机的情况下,文献[3]提出了一种基于进化算法的组合算法来解决复杂的动态优化问题。在确定性需求下,文献[4]提出转移支付的协调策略来协调各零售商的订货,实现统一配送。文献[5]研究了直接配送下随机需求库存路径问题,给出了存在车辆数和客户库存容量约束时的最优平稳策略及其算法。文献[6-7]则采用动态规划、混合整数规划以及随机规划等数学规划方法研究了2类具有滚动周期的随机库存路径问题。

上述已有IRP模型均假设市场需求与产品库存量无关,但是市场研究者发现,某些产品的需求受其货架展示量的影响,商品展现常常能刺激顾客的购买欲望[8]。文献[9]在需求依赖于当前库存水平的假设下,研究了单一生产商向单一销售商提供数量折扣的供应链完美协调。文献[10]在需求依赖于当前库存水平并且销售商库存容量有限的假设下,研究了供应商通过信用支付策略协调供应链的问题。文献[9-10]研究了需求依赖于库存水平的供应链协调问题,但均未考虑产品运输路径的优化问题。而实际上,运输费用是客观存在的,且在供应链的成本中占有很大比例。

本文在零售商市场需求依赖于其当前库存水平的假设下,研究了由单供应商和多零售商组成的非一体化供应链的库存路径问题。首先根据供应商主导的Stackelberg对策结构(即供应商向零售商宣布价格,零售商根据价格确定相应的订货量),对供应链成员间的最优决策进行了分析,然后在联合决策时,通过改进的最邻近算法统筹安排车辆运输路线,提高供应链整体利润,再通过调整批发价格,重新分配供应链利润,实现供应链的协调。

1模型的假定与记号

本文主要假定如下:

(1) 考虑由1个供应商和n个零售商组成的2层供应链,供应商生产并批发某一产品给零售商,并假定供应商为该供应链的核心企业,供应商了解市场需求信息及零售商所发生的各项成本。

(2) 假定零售商按标准的经济订货批量(economic order quantity,EOQ)模型来确定其最优订货策略,零售商的库存容量足够大,不允许缺货,零售商的地理位置已经确定,且1个零售商只需要1辆车为其服务。

(3) 假设供应商与零售商之间实行“批对批”策略,因此在供应商处不考虑库存费用。

(4) 配送车辆是同质车辆,且每辆车的容量都是U。

(5) 零售商将购买的商品全部展示销售,且假定其需求率依赖于当前库存水平,即

其中,α、β分别为尺度参数和形状参数,α>0，0<β<1；I(t)为零售商在t时刻的库存水平。

模型使用的符号如下:假设有1个供应商,n个零售商,以0表示供应商,S表示零售商的集合,即S={1,2,3,…,n};c为供应商的单位产品成本;p为零售商单位产品的市场售价;wi为供应商提供给零售商i的原批发价格;wd为供应商采取价格协调策略后,单位产品的批发价格;qi为零售商i的订货量;Ti为零售商i的订货周期;T为联合决策时,供应商对零售商的统一送货周期;X为供应商的统一送货周期备选集合;Qi为送货周期为T时供应商给零售商i的送货量;a为车辆行驶单位距离的运输费用;lij为从点i到点j的距离,i,j=0,…,n;h为零售商单位产品单位时间的库存费用;K为零售商的固定订货费用;M为车辆启动费用;Ps为供应商的平均利润;Pr为零售商的总的平均利润;Psc为供应链整体的平均利润;在车辆k服务节点i后立即服务节点j的情况下xijk=1,其他情况下均为0,其中,k=1,…,m;i，j=0,…,n;零售商i的任务由车辆k完成时，yki=1，其他情况下均为0。

2模型的建立

根据假设,零售商i处的库存水平变化的微分方程为：

(1)

由边界条件Ii(0)=qi,可得(1)式的解为:

(2)

由此可知，零售商i的每个订货周期长度为:

(3)

2.1独立决策

在独立决策时,对于供应商给定的任何批发价格,零售商均以平均利润最大化为目标设置最优订货量,此时零售商的利润为其销售收入减去批发成本、库存成本和订货费用,因此零售商i的平均利润为:

(4)

(5)

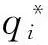
(6)

(7)

由(5)式、(6)式可得:

(8)

则由dPsi/dwi=0,可得:

(9)

将(9)式带入(5)式可得:

(10)

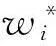
(11)

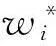
则单位时间零售商的总利润为:

(12)

单位时间供应商的总利润为：

(13)

单位时间供应链的整体利润为：

(14)

2.2联合决策

此时供应商为各零售商确定送货周期和送货量,则供应商可以统筹安排运送路线以降低配送费用,提高整个供应链的利润,且供应商可以通过价格策略对供应链利润进行重新分配,保证供需双方均能提高利润。设供应商调整后的送货周期为T,T∈X,X为供应商的统一送货周期备选集合。各点的送货量为Qi,由假设可知:

(15)

并设共需m辆车,m≥1。在T时间内,零售商i的平均利润为:

(16)

单位时间零售商的总利润为：

(17)

单位时间供应商的总利润为：

(18)

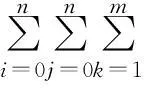
(19)

(20)

(21)

(22)

(23)

(24)

(25)

(19)式为车辆装载质量限制,(20)式、(21)式表示每个客户只被服务1次,(22)式表示只有1辆车为某客户服务。

单位时间供应链的整体利润为:

(26)

对非一体化供应链进行联合决策时,在使得供应链整体利润尽可能大的情况下,还要保证供应商和零售商的平均利润均能得到提高。为了说明供应商可以通过调节批发价格来保证供需双方平均利润都有所增加，本文给出以下定理1。

定理1对于非一体化供应链的IRP时,为保证供应商和零售商均愿意合作,则wd的下界设定为:

对于每个零售商,供应商提供的批发价格wd上界为:

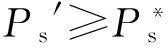
(27)

即得:

(28)

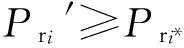
(29)

3算法设计及算例

本文通过对传统的最邻近算法进行改进,使之适用于非一体化供应链IRP的求解。改进的最邻近算法将在降低运输费用、提高供应链整体利润的前提下,给出相应的价格策略,实现供应链的协调。

3.1算法描述

由于传统的最邻近算法是针对旅行商问题(travelling salesman problem,TSP)的,不适用于求解多条线路,且没有考虑车辆的容量限制,为了适应本问题的求解,可以将其改进,得到改进的最邻近算法如下。

(1) 对n个零售商设置访问,d=0。

(2) 取原点0(供应商)作为线路的起点。

(3) 寻找与上一次加进线路中的点距离最近且d=0的零售商,判断该零售商加进线路中是否满足车容量限制,若满足则把该零售商加到线路中,d=1;否则不加入,d=-1。

(4) 重复步骤(3),直到所有的零售商均已考虑,即d≠0,则得到1条线路。

(5) 若存在d=-1的点,则将所有d=-1的零售商改为d=0,转到步骤(2),否则转到步骤(6)。

(6) 根据所确定的线路,求车辆运输路线的总长,进而根据(26)式求单位时间供应链的整体利润Psc′,根据定理1求出wd的取值范围。

(7) 对于每个T∈X,重复以上步骤都会得到一个Psc,寻找其中最大的一个Psc,得到最优解T、Psc、wd。

3.2数值实验与分析

为说明本模型的求解过程及其实际应用,现给出一个具体算例。

有1个供应商(编号为0),提供单一产品,有8个零售商(编号为1~8),它们的市场需求函数为Di(t)=αiI(t)βi,(c,p,h,a,K,M,Q)=(280,500,7,1,20,100,3 000),(α1,α2,α3,…,α8)=(40,42,45,43,50,35,48,50),X=(3,4,5,6,7),(β1,β2,β3,…,β8)=(0.3,0.2,0.2,0.3,0.2,0.3,0.3,0.3),各零售商与供应商及零售商之间的距离见表1所列。

(1) 独立决策时,供应商严格按照各零售商的需求送货,组织运输。总共送11 325单位产品。

不采用IRP时,由 (12)~(14)式可得:

Pr=79 148，

Ps=291 003，

Psc=370 151.3。

(2) 联合决策后,供应商在满足零售商需求前提下,合理安排配送方案以减少运输成本,为了使供应商与零售商均能提高利润,供应商重新调整批发价格为wd。根据改进的最邻近算法,可以得到供应商的配送路线。为了表示方便,配送路线中的节点次序代表其配送的先后次序,并用(零售商编号,配送量)表示每个节点。

T=3时,共需2辆车,其配送路线为((4,622),(3,348),(2,319),(5,397),(8,772),(6,464))和((1,561),(7,728)),路线总长为1 310,由(26)式,Psc′=295 867

表1　各零售商与供应商以及零售商之间的距离

T=4时,共需3辆车,其配送路线为((4,938),(3,499),(2,458),(5,569))、 ((1,846),(7,1 098),(6,699))和((8,1 164)),路线总长为1 980,Psc′=299 304

T=5时,共需4辆车,其配送路线为((4,1 291),(3,659),(2,605))、((1,1 164),(7,1 510))、((6,962),(5,752))和((8,1 601)),路线总长为2 233,Psc′=350 285

T=6时,共需5辆车,其配送路线为((4,1 675),(3,828))、((1,1 510),(2,760))、((6,1 248),(5,945))、((7,1 959))和((8,2 077)),路线总长为2 493,Psc′=370 591>Psc。

这说明在配送周期T=6时,供应链整体利润增加了,这是由于在该配送周期供应商通过统一配送,节省的运输费用大于零售商增加的库存成本或因市场需求流失而造成的损失。此时供应商可以通过重新调整批发价格,使得供应商与零售商均能提高利润。

T=7时,共需6辆车,其配送路线为((4,2 087))、((1,1 882),(3,1 004))、((2,921),(5,1 145))、((6,1 555))、((7,2 442))和((8,2 589)),路线总长为2 621,Psc′=387 758>Psc,由定理1知，wd的下限为439.862 2,对于各零售商,wd的上限依次为471.123 5、455.778 4、465.820 5、471.123 4、465.682 1、471.110 5、471.101 7、471.092 7。

本文给出了T=3和T=7时各零售商的配送路线示意图,如图1所示。

图1　各零售商的配送路线示意图

对于该算例,当T=7时,供应链整体利润更大,因此供应商选择送货周期为7。从算例可见,在非一体化供应链下,采用库存、路径的联合优化,提高供应链整体利润,再通过价格策略将提高的利润进行划分,使得供应商与零售商均能提高利润,保证各方愿意合作。

4结束语

经典的库存路径问题通常均假定产品的需求率是固定的或随机的,本文通过假定需求率依赖于零售商当前库存水平而建立了相应的模型。在模型中不允许短缺发生,首先研究了独立决策时,供需双方的最优决策,然后在联合决策时供应商通过降低运输费用,提高供应链的整体利润,再通过价格策略实现供应商和各零售商多赢。

研究结果表明，该协调策略不仅对供应商有利而且也能改善销售商的利润。本模型可进一步研究易腐品的协调、多层供应链及多供应商等几种情形。

[参考文献]

[1]Federgruen A,Zipkin P.A combined vehicle routing and inventory allocation problem [J].Operations Research,1984,32(5):1019-1037.

[2]刘桂庆,周永务,李凯.基于价格策略的非一体化供应链IRP研究[J].系统仿真学报,2008,20(6):1408-1412.

[3]Shukla N,Tiwari M K,Ceglarek D.Genetic-algorithms-based algorithm portfolio for inventory routing problem with stochastic demand[J].International Journal of Production Research,2013,51(1):118-137.

[4]张凯清,周永务.基于转移支付的非一体化库存路径问题协调模型[J].合肥工业大学学报:自然科学版,2010,33(3):453-459.

[5]赵达,李军,马丹祥,等.直接配送下随机需求库存:路径问题最优平稳策略及其算法[J].中国管理科学,2014,22(6):61-68.

[6]Bertazzi L,BoscoA,GuerrieroF,et al.A stochastic inventory routing problem with stock-out[J].Transportation Research Part C:Emerging Technologies,2013,27(2):89-107.

[7]Yu Y G,Chu C B,Chen H X,et al.Large scale stochastic inventory routing problems with split delivery and service level constraints[J].Annals of Operational Research,2012,197(1):135-158.

[8]Levin P I,McLaughlin C P,Lamon R P,et al.Productions/operations management:contemporary policy for managing operating systems [M].New York:McGraw-Hill,1972:373.

[9]闵杰,周永务.库存水平影响需求变化的供应链协调[J].复旦学报:自然科学版,2007,46(4):523-533.

[10]Zhong G Y,Zhou Y W.Improving the supply chain’s performance through trade credit under inventory-dependent demand and limited storage capacity[J].International Journal of Production Economics,2013,143(2):364-370.

(责任编辑闫杏丽)

Research on IRP of decentralized supply chain with stock-dependent demand

LIU Jun,LIU Gui-qing

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

Abstract:For a decentralized supply chain consisting of a single supplier and multiple retailers, the inventory routing problem(IRP) with the stock-dependent market demand of retailers is considered. In a distributed system, the profit models of the supplier and retailers are established and a modified nearest neighbor algorithm is proposed to reduce transportation cost and enhance the whole profit of the supply chain. A proper pricing strategy is used to realize multi-win and improve the coordination of supply chain. Numerical example is given for the simulation calculation and analysis.

Key words:stock-dependent demand; decentralized supply chain; inventory routing problem(IRP); supply chain coordination; pricing strategy

中图分类号:O227

文献标识码：A

文章编号：1003-5060(2016)02-0283-06

Doi:10.3969/j.issn.1003-5060.2016.02.027

作者简介：刘俊(1988-),男,安徽阜南人,合肥工业大学硕士生;刘桂庆(1978-),女,安徽和县人,博士,合肥工业大学副教授,硕士生导师.

基金项目：国家自然科学基金资助项目(71101002);高等学校博士学科点专项科研基金资助项目(20120111120013)和合肥工业大学科学研究发展基金资助项目(2013HGXJ0234)

收稿日期：2015-01-07；修回日期：2015-04-28