基于OpenGL的六关节机器人运动学分析与仿真
2016-04-12KinematicsanalysisandsimulationofsixjointrobotbasedonOpenGL
Kinematics analysis and simulation of six joint robot based on OpenGL
欧阳旭东,胡晓兵,付柯锦,徐兴伟
(四川大学 制造科学与工程学院,成都 610065)
OUYANG Xu-dong, HU Xiao-bing, FU Ke-jin, XU xing-wei
基于OpenGL的六关节机器人运动学分析与仿真
Kinematics analysis and simulation of six joint robot based on OpenGL
欧阳旭东,胡晓兵,付柯锦,徐兴伟
(四川大学 制造科学与工程学院,成都 610065)
OUYANG Xu-dong,HU Xiao-bing,FU Ke-jin,XU xing-wei
摘要:对于自主设计的六关节机器人,运用D-H法建立机器人的关节坐标系,求解出正逆运动学方程,在Visual C++环境下利用OpenGL图形库构造机器人实体仿真模型,并进行机器人正逆运动学仿真。仿真结果直观反映了机器人末端位姿和动态过程,验证了机器人运动学求解的正确性,机器人结构设计合理,为研究动力学分析、轨迹规划奠定了基础。
关键词:机器人;运动学;OpenGL;仿真
0 引言
机器人的运动学分析是研究机器人学的基础,是确定机器人在特定工况下动力学分析、轨迹规划和运动控制的前提[1]。为实现机器人运动学的快速求解与分析,需要使用仿真软件对机器人进行动态仿真,最常用的是MATLAB中的Toolbox工具箱,功能齐全,但是图形过于简单,不能直观有效的反映机器人的末端位姿与动态过程[2,3]。由于OpenGL是高性能的开放式图形库技术,具有强大的图形系统和优越的应用程序界面,因此在仿真分析上得到了广泛的应用[4]。
本文利用Visual C++和OpenGL混合编程技术,构造出机器人的实体仿真模型,并进行正逆运动学仿真,对机器人运动学模型进行验证。
1 六关节机器人运动学分析
1.1机器人D-H运动学模型的建立
在进行机器人的运动学分析时,Denavit-HartenBerg表示法是种简单且广泛应用的方法[5]。自主设计的六关节机器人,其结构模型如图1所示。运用D-H法对机器人进行运动学建模,图2为建立的机器人连杆坐标系,相应的各杆件结构参数和运动参数如表1所示,其中di,ai和αi均为已知,θi随着关节i的运动而发生变化。

图1 六关节机器人结构模型

图2 六关节机器人连杆坐标系
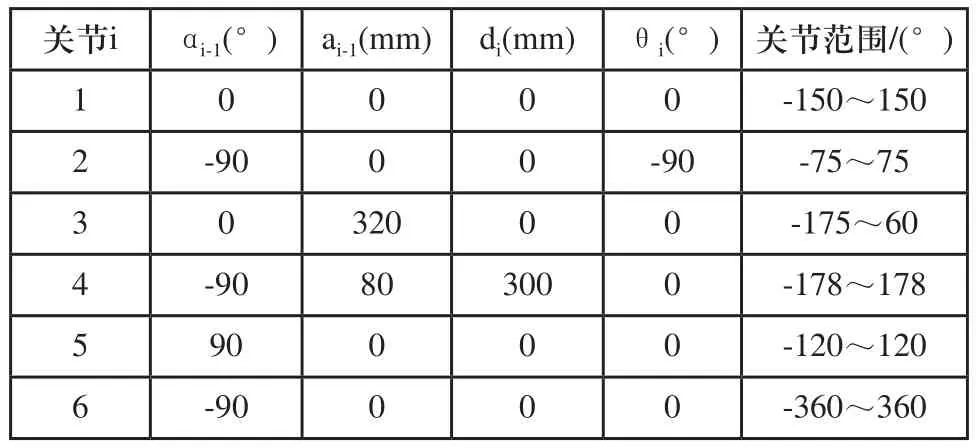
表1 六关节机器人的连杆参数
1.2机器人运动学正解
机器人运动学正解是指已知机器人各个关节的角度,求解机器人末端执行器坐标系在基础坐标系中位置和姿态的过程。在建立的D-H模型中,第i连杆坐标系相对于第i-1连杆坐标系的其次变换矩阵,满足以下公式:


1.3机器人运动学逆解
机器人逆运动学是指已知机器人的末端执行器的位姿,求解机器人各个关节角度变量的问题,逆运动学算法的精度直接影响到机器人的补偿精度[6]。利用关节变量所对应的逆矩阵分别去左乘运动学方程公式(2)的两边,得到关节变量的函数方程,然后让方程两边的元素相等就可以把各个关节变量分离出来,计算出它们的角度。

同理可求得:

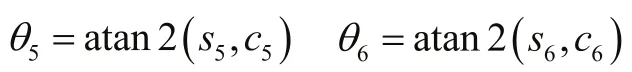
其中,角度θ4是在θ4≠0的前提下求得,且:


2 运动学仿真
图3为六关节机器人的运动学仿真流程图。首先在Visual C++中生成单文档的应用程序,设置相应的工程环境,然后调用OpenGL软件包。在完成维图形应用环境初始化以后,利用Draw()函数中的glTranslatef()和glRotatef()完成机器人坐标系的转换;利用auxSolidBox()和gluCylinder()函数,按照设计的机器人尺寸对机器人各个部件进行实体绘制,装配后得到机器人的实体仿真模型,然后就能进行机器人运动学正逆解的计算和仿真。

图3 六关节机器人运动学仿真流程图
为实现系统运动学仿真,在VC++界面上添加Text、Button等控件,用以实现输入、输出及图形仿真。最后得到机器人正运动学仿真界面(图4)和机器人逆运动学仿真界面(图5)。

图4 机器人正运动学仿真界面

图5 机器人逆运动学仿真界面
2.1正运动学仿真
在正运动学仿真界面中输入表2中的输入值,点击“运动学正解”按钮就能得到机器人末端执行器的位姿参数。输出结果见表2的输出值列,输出值仅列出向量ox,oy,oz和向量ax,ay,az的值,因为nx,ny,nz可以通过向量点乘求得。点击“图形仿真”即可得到机器人的当前位姿,仿真结果如图6(a)和图6(c)所示。

表2 机器人正运动学求解
2.2逆运动学仿真
在机器人逆运动学仿真界面中,将表2的输出值变成逆运动学求解中的输入值,点击“逆运动学求解”得到机器人各个关节角度的可能值。在求解过程中,角度转动范围检验会舍去不符合要求的解,将最后得到的解列入输出值中,如表3所示。可以看出,逆运动学求出的解其中组就是正运动学求解(表2)的输入值,由此验证了机器人逆运动学求解的准确性。

表3 逆运动学求解

图6 机器人仿真结果
3 结论
本文利用D-H法建立机器人连杆坐标系,根据运动学模型求解出机器人正逆运动学方程,在VC++环境下利用OpenGL图形库构造机器人实体仿真模型,完成了机器人的运动学仿真,仿真结果直观反映了机器人位姿和动态过程。并且利用具体数据验证了正逆运动学求解及仿真的正确性,为进步研究动力学分析、轨迹规划奠定了基础。
参考文献:
[1] 刘鹏,宋涛,贠超,等.焊接机器人运动学分析及轨迹规划研究[J].机电工程,2013(4):390-394.
[2] 陈世健,张铁.基于Matlab的喷涂机器人运动学分析[J].机电产品开发与创新,2008(5):4-5.
[3] 左富勇,胡小平,谢珂,等.基于MATLAB Robotics工具箱的SCARA机器人轨迹规划与仿真[J].湖南科技大学学报(自然科学版),2012(02):41-44.
[4] Dave Shreiner.OpenGL programming guide[M].China Machine Press,2010.
[5] Denavit J,Hartenberg R S. A kinematic notation for lower pair mechanisms based on matrices[J].ASME Journal of Applied Mechanics,1955,22(2):215-221.
[6] 刘松国.六自由度串联机器人运动优化与轨迹跟踪控制研究[D].浙江大学,2009:22-29.
[7] 王伟,谢明红,周国义.6-DOF工业机器人逆解优化及其工作空间的研究[J].机械与电子,2011(1):57-60.
作者简介:欧阳旭东(1989 -),男,四川绵阳人,硕士研究生,研究方向为工业机器人与机器视觉。
基金项目:四川省科技支撑计划项目(2014GZ0117)
收稿日期:2015-03-29
中图分类号:TH12
文献标识码:A
文章编号:1009-0134(2016)03-0038-03
