基于SVR的股市预测与择时研究
2016-04-11张鹏
张 鹏
(太原工业学院理学系, 山西 太原 030008)
基于SVR的股市预测与择时研究
张鹏
(太原工业学院理学系, 山西太原030008)
[摘要]本文首先阐述支持向量回归机原理,在此基础上建立了SVR预测模型,以HS300指数数据为测试样本,分析了SVR模型在时间序列预测问题中的优势,并在此基础上进行了交易实验.结果表明:支持向量回归机适用于预测股市大盘的短期走势,并能够得到比较好的预测效果.
[关键词]机器学习;支持向量回归机;时间序列
众所周知,股票市场是非线性动态的复杂系统,利用传统的线性时间序列分析方法(如ARMA、GARCH等)对其研究并不能得到理想效果,而近些年兴起的机器学习算法在对非线性时间序列的分析中表现出极大优势.作为在数据挖掘算法中较为成熟的支持向量机算法,其在很多领域均能成功处理非线性回归(时间序列)和分类(判别)等诸多问题.
1支持向量回归机基本原理
支持向量机算法(support vector machines,SVM)最初是解决模式识别、特征提取等问题,都属于支持向量机分类(SVC)问题[1].由于它具有强泛化能力而被推广应用于解决预测类问题,称为支持向量回归机(SVR).该理论将回归问题转化为二次规划(quadratic programming,QP)问题,属于黑匣子理论.
1.1支持向量机SVM的基本思想
首先将低维线性不可分训练数据集通过核函数映射到一高维特征空间(称为Hilbert空间);然后在特征空间进行线性可分的分类或回归,这样高维空间输出层上的线性回归或分类就对应着低维空间输入层的非线性回归或分类.大量理论已经证明,隐藏层维数如果足够高,支持向量机就能够逼近任意的非线性关系,并且核函数的使用能减少隐层的高维所带来的计算复杂性等一系列问题[2].
该算法的基本原理即为在所有的超平面中搜索一个最优分离面.该超平面不仅能准确分类,还能使超平面两侧的间距达到最大化.
1.2支持向量回归机SVR
利用支持向量机做回归与做分类大体相同,区别在于:SVC的输出变量是分类型,而SVR的输出变量是连续型.SVC是通过最优分离超平面使两类样本尽可能分开,而SVR是希望所有样本点距离超平面的总偏差最小,由此看出SVR实质上就是一个最优规划问题.
1.2.1线性回归情形

s.t. f(xi)-yi≤ε+ξi
ξi≥0,ξi′≥0,i=1,2,…,n
其中C(大于0) 是对ε以外样本的惩罚,故称为惩罚参数[4];ξi,ξi′称为松弛变量,表示训练样本拟合误差ε时的损失.
根据Karush-Kuhn-Tucker条件[5],通过引入拉格朗日乘数,上述问题就转化为对偶问题(dual problem):
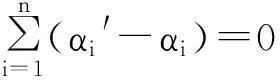
αi′,αi∈[0,C],i,j=1,2,…,n
1.2.2非线性回归情形
非线性回归首先是通过核函数将低维非线性问题转化为高维空间的线性问题,然后再利用线性回归情形分析.
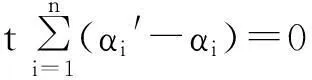
αi′,αi∈[0,C].i,j=1,2,…,n
目前该算法中常用的核函数有3种类型,分别为线性核、多项式核、高斯核,一般形式分别为
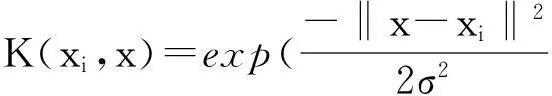
2构建SVR预测模型
2.1建模前的准备
(1)数据的选取.由于时间序列的特殊性,数据的选取是建模前需考虑的一个重要问题,尤其不能选取特殊时段,这样将会失去一般性.本文数据来源于wind资讯,原始数据指标体系为沪深300指数2010年1月4日到2012年12月31日的收盘价等时间序列,如表1所示.相关指标有基础指标的前5日收盘价、最高价、最低价、成交量的对数,技术指标MA(10)、KDJ、RSI、BIAS、WR、PSY共计14个因子.

表1 数据集
(2)滚动预测.为了能将最新的市场信息及时反映在模型中,并且消除市场周期性的影响,本文采用滚动时间窗口进行建模,又考虑到时间窗口最好不要超过一个交易年,故选取240个交易日作为时间窗口,即若当前日期为T,则样本期选为T-1到T-240,找到样本期内最优参数,进而利用T日的数据预测T+1日的收盘价.

上述公式表示基于t时期的j步向前的价格预测值为给定t时期前所有信息的j步向前真实价格的期望值.这里,t=N1,…,N-j,且令j=1,…,5,也就是说,最短预测未来一天的收盘价,最长预测5天的收盘价(如果t表示每日).可见,预测区间固定为j向前,而预测起点t择时逐步向后推移,因而是动态的.
2.2建立SVR预测模型
(1)数据清洗.本文采用Pearson相关性检验对解释变量进行筛选.鉴于股市中的变量之间可能存在非线性关系,本文对原始数据不完全直接进行Pearson检验,而对于线性不明显的变量采取一些变换,最终确定因子备选库中含有13个解释变量,基础指标的前5日收盘价、最高价、最低价、成交量的对数,技术指标MA(10)、KDJ、RSI、BIAS、PSY共计13个因子.
(2)数据标准化.为避免因为变量间因数量级差别较大而造成模型预测误差失真的现象,本文统一对数据采用极差标准化处理.
(3)变量的优化组合——主成分分析.如果要真实、完整地反映实际问题,往往需要很多变量以及样本,而各个变量之间并非独立的,它们之间或多或少存在相关性.这样不仅使得研究变得复杂,还可能导致预测精度降低.本文运用主成分分析法将规范化后的变量压缩为少量几个互不相关的变量,计算每日的13个指标值,并对其运用主成分分析.当主成分个数为6个时,累计方差贡献率达到98.79﹪,包含信息的完整性程度较好,因而选取前6个主成分作为输入变量.
(4)核函数和有关参数的选择.本文寻找最优的C和ε的主要思想是:首先将C和ε界定在一定范围以内([2-6,26]),然后用交叉验证进行搜索使得MSE达到最小.为了避免因为惩罚参数C太大引起过学习,所以本文选择的是具有最小C的组合C和ε.这样可以在一定程度上利于外推.筛选结果为Gaussian核函数,C和ε都是0.25.
2.3结果分析
经过变量的筛选组合以及模型参数的选取最终完成模型的建立,并用2012年的数据进行测试.SVR预测值与真实值及相对误差比较结果如图1、图2所示.
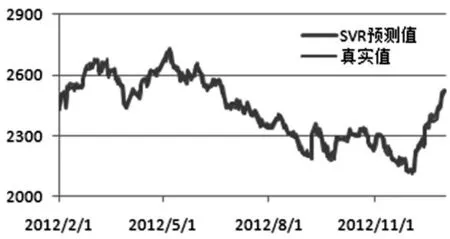
图1 预测值与真实值对比
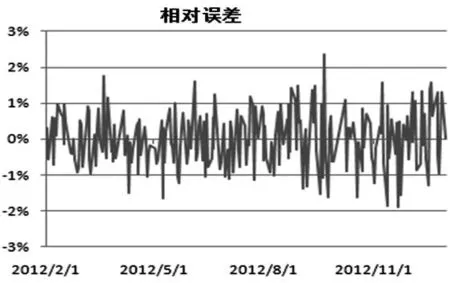
图2 SVR预测相对误差
从图1可以看出,SVR的预测值基本靠近真实值.图2显示,预测值相对于真实值的误差绝大多数在2﹪以内,说明本文建立的SVR预测模型是有效的.
2.4构建时隔一周交易日的预测模型
假设当前日为T日,本文以第T+1、T+2、T+3、T+4、T+5日的收盘价分别作为输出变量构建5个模型,仍然采取240个交易日为滚动时间窗口,然后对这5个模型进行比较,如表2所示.
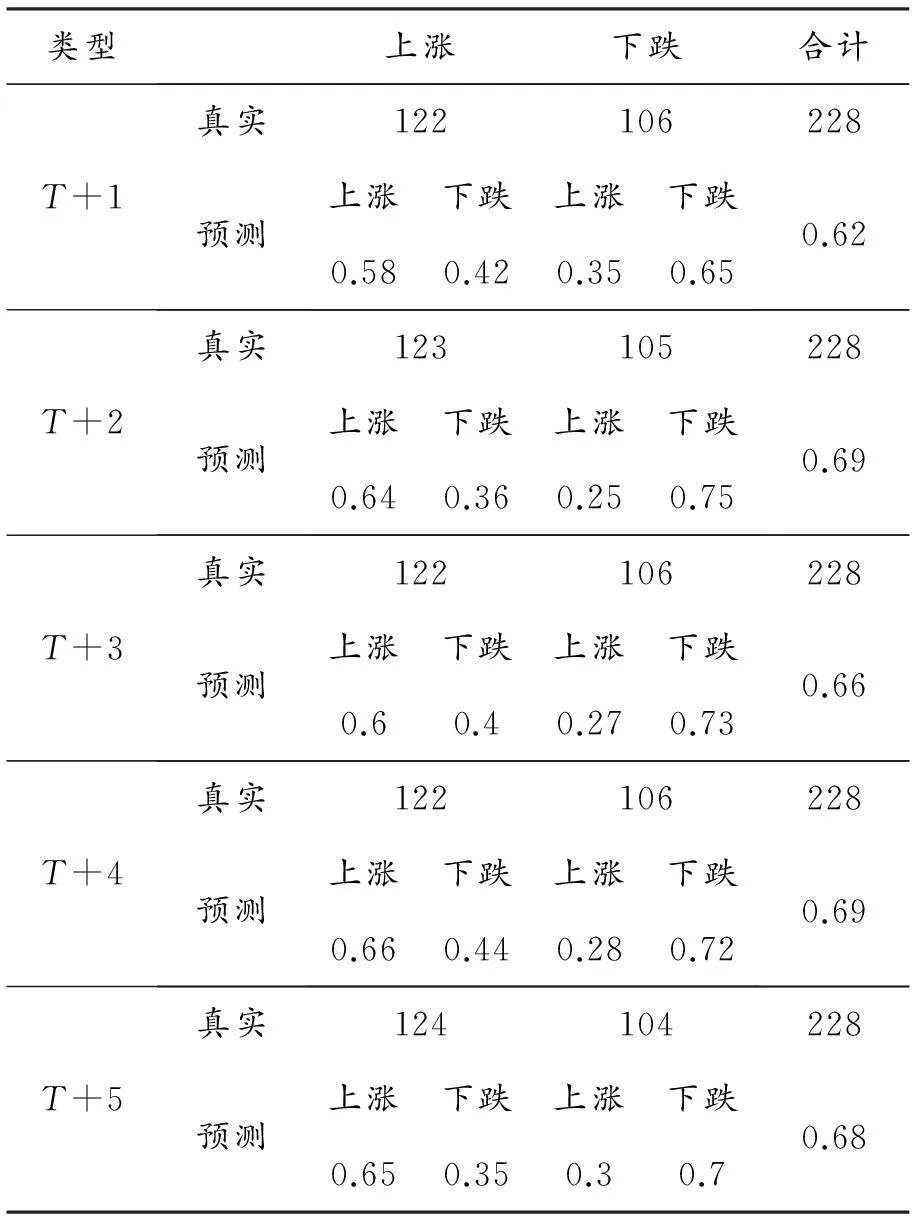
表2 五种预测结果与真实对比
从表2看出,SVR择时模型在T+1、T+2、T+3、T+4和T+5日5种情况下,都是对下跌的预测精度要高于上涨的.在1年的测试数据下,SVR择时模型均能保持较高的准确率,5种类型的预测中,对于下跌的预测准确率均能保持在0.65以上,对于上涨的预测准确率保持在0.6以上,对整个市场的预测则能保持在0.62以上.所以,该模型对预测HS300指数具有可行性.
2.5模拟交易
择时本质上是预测,即在预测的基础上做择时策略.SVR模型预测的结果只是给出一个涨跌的信号,然后在此基础上选择合适的时刻进行交易.
基于一般性的考虑,本文以HS300指数作为标的资产,在实际操作中,考虑到冲击成本与交易成本,选择T+5日作为实际的交易时间,指定如下交易规则:
(1)如果预测标的是上涨的记为1,相反下跌的记为-1;
(2)如果预测为上涨,并在市场行情低于T日的收盘价时买入并持有;
(3)如果涨幅超过2﹪(止盈点)则卖出,否则到T+5日自动平仓;
(4)设定止损点为2﹪,即如果亏损2﹪则平仓.
(5)对于反向操作——做空,2和3则采取相反的操作,其余亦同.
这样的交易规则可以避免因为股市的暴涨或暴跌带给人们一时的收益或损失,该操作进行的是长期交易.图3表示在2012-02-01至2012-12-31期间的按照上述策略进行交易的累计净值情况.
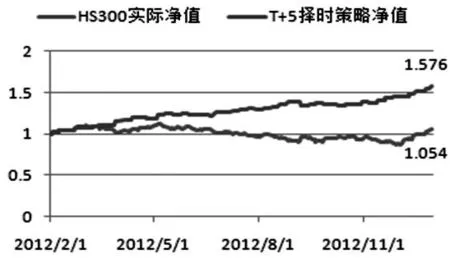
图3 2012年HS300和SVR择时策略的累计净值
T+5日SVR择时策略对HS300指数同时采用多空操作, 通过利用被动挂单的方法, 只要价格达到合适的位置则选择开仓,如果没有达到开仓条件则继续等待,如果开仓后价格没有触及止盈点或止损点则以最后时刻平仓.从图3看出,从2012年2月1日至2012年12月31日,HS300净值从1增长到1.054,而通过SVM择时策略进行交易,净值从1增长到1.576.
3结语
本文所构建的SVR预测模型创新点是采用滚动预测方案,即不同于处理静态数据那样所采用的固定预测方案.该预测方案采用迭代估计而非一次性估计和预测.
[参考文献]
[1]ETHEM ALPAYDIN.机器学习导论[M].范明,昝红英,牛常勇,译.北京:机械工业出版社,2014.
[2]KIM K J. Financial time series forecasting using vector machines[J]. Neurocomputing,2003 (55):307-319.
[3]边肇祺,张学工.模式识别[M].北京:清华大学出版社,2002.
[4]田盛丰. 基于核函数的学习算法[J]. 北方交通大学学报, 2003(2):1-8.
[5]BURBIDGE R, TROTTER M, BUXTON B, et al. Drug design by machine learning: support vector machines for pharmaceutical data analysis[J].Computer and Chemistry, 2001(1):5-14.
[6]TROTTER M W B, BUXTON B F, HOLDEN S B. Support vector machines in combinatorial chemistry[J]. Measurement and Control, 2001(8):235-239.
(责任编辑穆刚)
Research of forecasting and timing in stock market based on SVR
ZHANG Peng
(Science Department, Taiyuan Institute of Technology, Taiyuan Shanxi 030008, China)
Abstract:This paper firstly expounds the principle of support vector regression machine, on the basis of which SVR forecasting model is established and then the advantages of SVR model are analyzed in time series prediction problem, regarding HS300 index as the test sample. Based on this, trading experiment is conducted to show that SVR is applicable to predict the short-term trends of stock market, and it can get a better prediction effect.
Key words:machine learning; support vector regression; time series
[中图分类号]C812
[文献标志码]A
[文章编号]1673-8004(2016)02-0148-04
[作者简介]张鹏(1989—),男,山西长治人,助教,硕士,主要从事数据分析、统计决策方面的研究.
[收稿日期]2015-10-18
