基于排队论的高速公路服务区停车位合理规模的计算

王　殊,徐英俊

(1.长安大学　经济与管理学院，陕西　西安　710064；2.河南工业大学　经济贸易学院，河南　郑州　450052；

3.吉林大学　交通学院，吉林　长春　130022；4.交通运输部科学研究院，北京　100029)



基于排队论的高速公路服务区停车位合理规模的计算

王殊1,2,徐英俊3,4

(1.长安大学经济与管理学院，陕西西安710064；2.河南工业大学经济贸易学院，河南郑州450052；

3.吉林大学交通学院，吉林长春130022；4.交通运输部科学研究院，北京100029)

摘要：鉴于传统的停车位数计算方法均基于车辆的到达时间间隔相同和服务时间不变的假设，无法保证实际的服务水平，在分析影响服务区停车位规模主要因素的基础上，引入排队理论，得出了停车场排队系统在稳态下的平均顾客数与服务强度及停车位数的关系，并基于服务水平给出了停车位规模的合理计算方法。实例分析表明，该方法能够合理地计算出服务区停车位的规模，为停车位规模的计算提供了新的思路。

关键词：交通工程;停车位测算;排队论;高速公路;服务区

0引言

高速公路服务区是保证车辆行驶安全、提高服务水平的不可缺少的基础设施。我国没有完善的高速公路服务区规划设计与功能布局指南。2000年颁布实施的《公路建设项目用地指标》[1]中对服务区的规模仅作了原则性限定。受其约束，我国服务区规划设计大都采用了紧凑型布局，绿化率低。在实际计算过程中，我国多借鉴《日本高速公路设计要领》(1991年版)中的方法[2]，在确定服务区规模时，首先根据主线交通量及驶入率等参数计算停车位数，然后根据停车位数计算与之相关的餐厅、休息、加油站、公共厕所等其他设施的规模。可见，停车位数的确定是计算高速公路服务区规模的核心内容。

服务区停车位数的传统计算方法是用主线预测交通量、服务区驶入率、高峰停车率三者之积再除以周转率得到[3-5]，但该推导过程基于如下假设：若车辆的到达时间间隔相同和服务时间不变，则计算出的设施规模恰好满足需求。然而，车辆和旅客到达的时刻以及所需要的服务时间在事先都无法确定而呈现随机性，故该方法无法保证实际的服务水平。因此，本文在分析影响服务区停车位规模的主要因素的基础上，引入排队理论，分析了停车场的服务水平，并基于服务水平给出了停车位规模的合理计算方法。

1服务区停车位规模的影响因素

影响服务区停车位规模的因素主要包括主线交通量及组成、服务区驶入率、高峰停车率、停车周转率4个因素。

1.1主线交通量及组成

交通量及交通组成是确定服务区停车位规模的主要因素之一，一般来说服务区所在位置断面交通量越大，服务区的驶入量越大，需要的停车位规模也越大。此外，随着人民生活水平的提高和小客车的普及，高速公路上小客车的比例将会增加，不同的车型具有不同的服务需求特征，比如小客车的驶入率、服务区逗留时间与货车有很大差别，因此在确定停车位规模时还应考虑交通流量组成及其变化趋势。

根据确定的预测年限、交通量增长率和基础年的交通量，对未来目标年的交通量进行测算。计算公式为：

(1)

式中，Qni为预测远景年车型i的平均交通量；Q0i为基础年的车型i平均交通量；γi为车型i的年平均交通量增长率；n为计算的远景年限。

1.2驶入率

服务区的驶入率是指驶入服务区的车辆数(辆/日)占服务区所在主线断面交通量(辆/日)的比例。驶入率主要由服务区间距决定，在主线交通量一定的情况下，服务区间距越大，驶入率越高，需要的停车位的规模也越大；相反，间距越小，驶入率越低，需要的停车位规模也越小。

目前，驶入率主要依据统计数据确定。文献[6]认为驶入率受车型、服务区间距、驾驶人和乘客的生理需求等影响，驾驶人连续驾驶的时间一般不超过3 h，因而得出驶入率公式：

Pi=KiA/3Vi,

(2)

式中,Pi为车型i车辆的驶入率；Ki为系数；A为高速公路服务区平均间距；Vi为车型i车辆的平均速度。

将主线不同车型的预测交通量与对应的驶入率相乘便得到服务区的驶入车辆数：

(3)

再将交通量折算成标准车型的交通量，计算公式为：

(4)

式中，Qe为标准车型驶入交通量(辆/日)；Qi为第i类车型的驶入交通量；Ei为第i类车型的折算系数。

1.3高峰停车率

服务区高峰率指服务区一天中一个小时内的最多停车数与一天中总停放车辆数的比值。车辆停靠高峰主要集中于中午、晚上吃饭的时间段[7]。计算公式为：

α=高峰小时停留车辆数/

日停车车辆数量。

(5)

1.4停车周转率

服务区停车周转率指服务区内每个停车位1小时内停放的车辆数，其计算公式为：

(6)

2服务区停车排队系统建模

进入服务区的车辆遵循随机到达，接受服务，离开的过程，可采用排队论模型分析其系统的运行特征：

(1)该排队系统的顾客是进入服务区的车辆，根据文献[8]的研究，顾客的到达时间间隔服从负指数分布，则顾客的平均到达率λ等于标准车型驶入交通量与高峰停车率之积：

(7)

(2)该排队系统的服务台是停车位，服务台的个数N即为停车位的数量。每个服务台的服务时间同样服从负指数分布，每个服务台的服务率即为停车周转率β。

(3)该排队系统为损失型排队系统，若顾客到达时所有服务台处于工作状态，则顾客会选择离开，驶入下一个服务区。

从上述分析可知，这是一个M/M/N/N排队系统，系统服务强度ρ为：

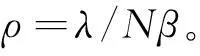
(8)

根据排队系统各个状态概率守恒[9-10]，通过求解状态转移概率矩阵，即得到系统的稳态概率。

系统中没有车辆的概率为：

(9)

系统中的平均顾客数量：

(10)

系统中恰好有k辆车的概率：

(11)

3服务区停车位规模计算步骤

式(10)给出了停车场的平均停靠车辆数与系统服务强度及停车位数之间的关系。若根据系统预定的服务水平确定了停车场的平均停靠车辆数，即能根据式(10)计算出停车位数。根据吉林省京哈高速公路实际调研数据及文献[11]的研究成果：当停车场泊位占有率低于30%时，车辆对车位的选择自由度很大，彼此干扰很小；泊位占有率在30%～70%之间时，车辆停靠容易但彼此有干扰；泊位占有率在70%以上时，车辆停靠比较困难并时常出现堵塞。因此，建议高速公路服务区停车场设计泊位占有率在70%以下。据此，便可计算停车场的停车位规模，步骤如下：

Step1：根据实际调研数据，利用式(1)～(2)、(5)～(6)分别计算远景年不同车型的平均交通量、不同车型的驶入率、高峰停车率及停车周转率，进而根据式(3)、(4)计算服务区平均每日标准车型驶入量，利用式(7)计算系统顾客平均到达率λ。

Step2：由于式(10)中停车场平均停靠车辆数计算公式为非连续变量，且计算公式复杂，因此难以用解析法直接求解，建议采用试算方法。为尽量降低试算迭代次数，停车场车位初始值采用式(12)确定：

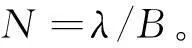
(12)

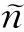
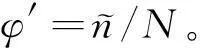
(13)

Step4：占有率φ′与期望占有率φ=70%一致性判断及车位数调整。可选定φ′与φ相对差值小于3%为一致性判定阈值，当φ′在[0.97φ,1.03φ]区间内时，此时N即为设计停车位；否则，当φ′>φ，增大N，当φ′<φ，减小N。

Step5：重复Step3、4，直到得到符合要求的停车位数N。

4实例应用

吉林省四平服务区是京哈高速公路上位于四平市境内的一个一类服务区。随着该段交通量的日益增加，该服务区现有的场站面积已经不能满足服务要求，亟需进行扩建。根据《京哈高速公路四平至长春段工程可行性研究报告》(2010)中的预测结果，2030年该段交通量为79 500 veh/d，不同车型比例预测如表1所示。

表1　京哈高速公路车型(pcu)比例预测结果

根据实际调查数据，得到四平服务区高峰停车率为0.08，平均周转率为2.4，不同车型的驶入率如表2所示。

表2　四平服务区不同车型驶入率预测

计算得到四平服务区单侧平均每日标准车型驶入量为5 092 veh，高峰小时驶入量412 veh。利用第3节的计算步骤，得到四平服务区的设计标准停车位为183个，而当前四平服务区的停车位规模是15年前建成的70个标准停车位。随着京哈高速吉林段交通量的日益增加，四平服务区的停车位已经很难满足停车需求，在高峰期出现了车辆排队的现象，服务水平下降明显。鉴于此，吉林省交通运输厅已经开展了京哈高速公路服务设施规模调整的研究。根据计算得到的停车位数和文献[12]中的方法，进一步计算得到四平服务区的总体规模为17.28 hm2，比原有占地面积增加9.27 hm2，改建后的服务区单侧平面布局如图1所示。

图1　四平服务区单侧平面布局图Fig.1　One-sided plane layout of Siping service area

5结论

随着经济的发展、人民生活水平的提高，高速公路服务区在整个高速公路系统中的作用越来越明显，但现有的服务区多数存在建设规模不合理，不能满足服务需求的问题，亟需更加科学合理的规模计算方法。服务区规模计算的核心是确定停车场的停车位数。传统的停车位数计算方法均基于假设：车辆的到达间隔相同和服务时间不变，然而，车辆和旅客的实际到达时刻及所需要的服务时间在事先都无法确定而呈现随机性，故该类方法的计算结果无法保证实际的服务水平。本文在分析影响服务区停车位规模主要因素的基础上，引入排队理论，得出了停车场排队系统在稳态下的平均顾客数与服务强度及停车位数的关系，并基于服务水平给出了停车位规模的合理计算方法。实例分析表明，该方法能够合理地计算出服务区停车位的规模，为停车位规模的计算提供了新的思路。

参考文献：

References:

[1]建设部， 国土资源部. 建标[1999]278号, 《公路建设项目用地指标》[M]. 北京：人民交通出版社，2000.

Ministry of Construction, Ministry of Land and Resources. MOC Standard NO. [1999]278, Land Usage Indexes for Highway Construction Projects [M]. Beijing: China Communacations Press,2000.

[2]汤毅. 高速公路服务区规划的关键技术研究[D]. 西安：长安大学，2008.

TANG Yi. Study on Key Technologies of Expressway Service Area Planning [D]. Xi’an: Chang’an University,

2008.

[3]张文成. 高速公路服务区规划研究[D]. 西安：长安大学，2006.

ZHANG Wen-cheng. Study on Planning of Expressway Service Area [D]. Xi’an: Chang’an University, 2006.

[4]蔡赫. 黑龙江省高速公路服务区规划设计研究[D]. 哈尔滨：东北林业大学, 2013.

CAI He. Research on Planning and Design of Expressway Service Area in Heilongjiang Province [D]. Harbin: Northeast Forestry University, 2013.

[5]赵君莉, 王建伟. 高速公路服务区服务水平评价方法研究[J]. 中外公路, 2010,30(4): 306-309.

ZHAO Jun-li, WANG Jian-wei. Study on Evaluation Methodology of Service Level of Expressway Service Area [J]. Journal of China & Foreign Highway, 2010,30(4): 306-309.

[6]吴斌. 高速公路服务区建设与运营管理模式研究[D]. 成都：西南交通大学, 2008.

WU Bin. Research on Construction and Operation Management Modes for Expressway Service Area[D]. Chengdu: Southwest Jiaotong University, 2008.

[7]申旺. 高速公路服务区规划与管理研究[D]. 西安：长安大学, 2010.

SHEN Wang. Study on Planning and Management of Expressway Service Area [D]. Xi’an: Chang’an University, 2010.

[8]赵君莉. 高速公路服务区服务水平评价方法[D]. 西安：西安电子科技大学，2008.

ZHAO Jun-li. Research on Evaluation Method of Facility Service System Levels of Expressway [D]. Xi’an: Xidian University, 2008.

[9]DEGROOT M H. Probability and Statistics, Fourth Edition[M]. Hong Kong: Pearson Education Asia Ltd., 2012.

[10]MEDHI J. Stochastic Models in Queuing Theory [M]. New York: Academic Press Inc., 1994.

[11]陈培. 高速公路服务区布局与合理规模研究 [D]. 天津：河北工业大学, 2011.

CHEN Pei. Research on Scientific Layout and Logical Scale of Expressway Service Area [D]. Tianjin: Hebei University of Technology, 2011.

[12]陈传德，邢利霞. 高速公路服务区合理规模的确定[J].公路，2010(11)：196-198.

CHEN Chuan-de, XING Li-xia. Determination of Reasonable Scale of Expressway Service Area[J]. Highway, 2010(11)：196-198.

Calculation of Reasonable Scale of Parking Spaces in Expressway Service Area Based on Queuing Theory

WANG Shu1,2, XU Ying-jun3,4

(1.School of Economics and Management, Chang’an University, Xi’an Shaanxi 710064, China;2. School of Economy and Trade, Henan University of Technology, Zhengzhou Henan 450052, China;3. School of Transportation, Jilin University, Changchun Jilin 130022, China;4.China Academy of Transportation Sciences, Beijing 100029, China)

Abstract：Traditional methods of calculating the number of parking spaces are all based on the assumption that the vehicles have the same arrival time interval and the same service time. These methods cannot guarantee the actual service level. Based on the analysis of the main factors that affect the parking spaces scale in the service area, by introducing the queuing theory, we obtained the relationship among the average number of customers, service intensity and the number of parking spaces in the steady state of the queuing system. Then, we proposed the reasonable calculation method of the parking space scale based on the service level. The case study shows that the method can calculate the parking space scale in the service area reasonably, which can show a new idea for the calculation of the parking space scale.

Key words：traffic engineering; parking space calculation; queuing theory; expressway; service area

文献标识码：A

文章编号：1002-0268(2016)03-0116-04

中图分类号：U491

doi:10.3969/j.issn.1002-0268.2016.03.019

作者简介：王殊(1977-)，女，黑龙江穆棱人，博士.(52574347@qq.com)

收稿日期：2015-02-10