随机多种群互惠系统的动力学行为
2016-04-11王丽顺李海红李海霞
王丽顺,李海红,李海霞
(1.中国国防科技信息中心,北京 100142;
2.东北师范大学数学与统计学院,吉林 长春 130024;
3.吉林建筑大学基础科学部,吉林 长春 130024;
4.长春光华学院商学院,吉林 长春 130024)
随机多种群互惠系统的动力学行为
王丽顺1,李海红2,3,李海霞4
(1.中国国防科技信息中心,北京 100142;
2.东北师范大学数学与统计学院,吉林 长春 130024;
3.吉林建筑大学基础科学部,吉林 长春 130024;
4.长春光华学院商学院,吉林 长春 130024)
[摘要]研究了带有随机扰动项的多种群互惠系统,证明了系统解的存在唯一性,给出了时间均值意义下的持久性概念,并指出所讨论系统在此意义下是持久的.
[关键词]随机微分方程;李亚普诺夫函数;平稳分布;持久性
互惠行为广泛存在于各种生物种群中,因其普遍性和重要性,使得对共生生物之间动态关系的研究一直占据着生态学研究的主导地位.[1-6]著名的种群动态模型——Lotka-Volterra互惠系统,已受到众多学者的大量关注和广泛研究.[5-6]
众所周知,Lotka-Volterra互惠系统可描述为

(1)
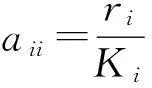
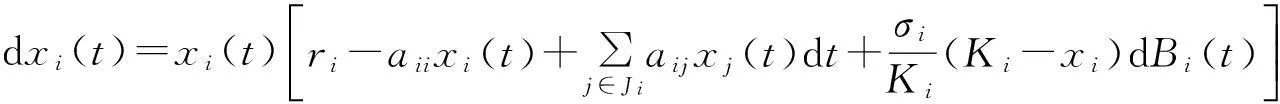
(2)
Goh[7]研究了两个种群的互惠系统,其模型为
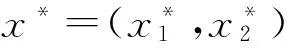

还有很多学者研究了互惠系统及其延展形式,如考虑时滞对互惠系统的影响等.[8]本文考虑随机互惠系统(1)的动力学行为.
1全局正解的存在性,唯一性
这里采用类似文献[9]中的证明方法得到系统(1)全局正解的存在唯一性.

P{τ∞≤T}>ε,
结合τ∞的定义,则存在整数k1≥k0,当k≥k1时有
P{τk≤T}≥ε.
(3)
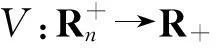


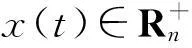

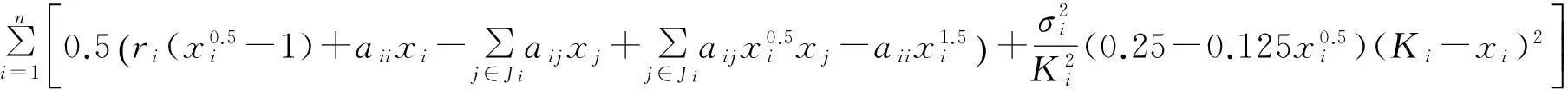
由于


从而
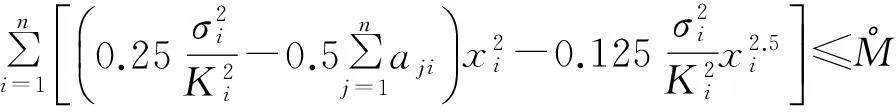
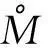

对上式两端取期望可得

(4)


于是由(1.4)式可得
V(x(0))+KT≥E[1Ωk(ω)V(x(τk,ω))]≥

其中1Ωk表示Ωk的特征函数.令k→∞,上式显然矛盾,因此τ∞=∞,a.s..定理1.1证毕.
2系统在均值意义下的持久性
在确定性系统中,文献[10]给出了均值意义下持久性的概念.这里,我们对随机系统也给出相应的定义.
定义2.1称系统(1.1)在时间均值意义下是持久的,是指

我们做如下假设:
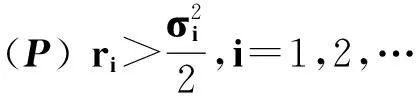
文献[10]研究了随机Logistic微分方程
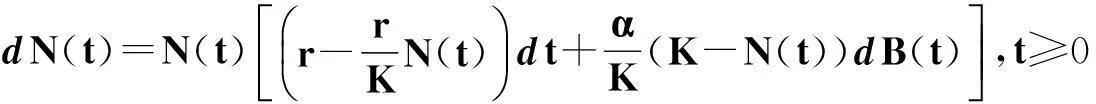
得到如下结论.
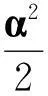
由随机比较定理可得
xi(t)≥φi(t),i=1,2,…,n,a.s.,
其中φi(t)是如下方程的解:

(5)
另外,Gray等[11]研究了如下带有随机扰动项的SIS传染病模型:
dI(t)=I(t)[(βN-μ-γI(t))dt+σ(N-I(t))dB(t)],
(6)
其中B(t)是一维的标准布朗运动,I(0)=I0∈(0,N),N是受传染病传染的人群数量.
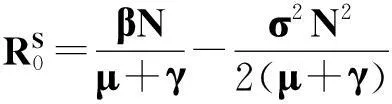

当假设(P)满足时,由引理2.1和引理2.2可知系统(5)存在平稳分布,并且

综上,我们有下面结论.
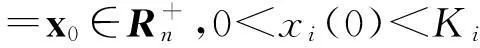
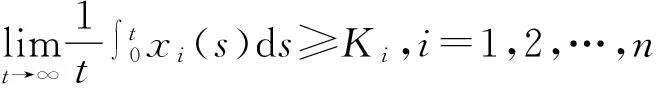
即系统(1)在均值意义下是持久的.
[参考文献]
[1]高芳.带有食饵避难的Leslie-Gower捕食者-食饵扩散系统的稳定性及最优税收[J].东北师大学报(自然科学版),2014,46(2):1-8.
[2]于新艳.污染环境下具有Beddington-DeAngelis功能性反应的捕食者-食饵系统的动力学行为[J].东北师大学报(自然科学版),2013,45(1):6-12.
[3]GOH B S. Global stability in many species system[J]. Amer Nat,1997,111:135-143.
[4]LI H H. Persistence and non-persistence of a food Chain model with stochastic perturbation[J/OL]. Abstract Appl Anal,2013[2014-04-29]. http://dx.doi.org/10.1155/2013/125089.
[5]KUANG Y,SMITH H L. Global stability for infinite delay Lotka-Volterra type systems[J]. J Differential Equations,1993,103:221-246.
[6]GLOPALSAMY K. Global asymptotic stability in a periodic Lotka-Volterra system[J]. J Austral Math Soc Ser B,1982,24:160-170.
[7]GOH B S. Stability in models of mutualism[J]. Amer Nat,1979,113:261-275.
[8]XIA Y H. Existence of positive periodic solutions of mutualism systems with several delays[J]. Adv Dyn Syst Appl,2006,36(2):209-217.
[9]XIA P Y. Persistence and nonpersistence of a nonautonomous stochastic mutualism system[J/OL]. Abstract Appl Anal,2013[2014-04-29].http://dx.doi.org/10.1155/2013/256249.
[10]JIANG D Q,ZHANG B X. Existence uniqueness,and global attractivity of positive solutions and MLE of the parameters to the logistic equation with random perturbation[J]. Science in China,2007,50(7):977-986.
[11]GRAY A,GREENHALGH D,HU L,A stochastic differential equation SIS epidemic model[J]. SIAM J Appl Math,2011,71:876-902.
(责任编辑:李亚军)
Dynamic behavior of a stochastic multiple species mutualism system
WANG Li-shun1,LI Hai-hong2,3,LI Hai-xia4
(1.China’s National Defense Science and Technology Information Center,Beijing 100142,China;2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China;3.Department of Basic Science,Jilin Construction University,Changchun 130024,China;4.School of Business,Changchun Guanghua University,Changchun 130024,China)
Abstract:In this paper,we analyze a n-species mutualism stochastic system. First of all,a unique positive solution of the system is considered which is essential in any population dynamics model. Then,we deduce a condition to keep the system being persistent in sense of time average.
Keywords:stochastic differential equation;Lyapunov function;stationary distribution; permanent
[中图分类号]O 175.14[学科代码]110·34
[文献标志码]A
[作者简介]王丽顺(1966—),女,博士,高级工程师,主要从事应用数学研究;通讯作者:李海红(1983—),女,博士,主要从事微分方程研究.
[基金项目]国家自然科学基金资助项目(11171350).
[收稿日期]2014-04-29
[文章编号]1000-1832(2016)01-0022-04
[DOI]10.16163/j.cnki.22-1123/n.2016.01.006
