高纯度分馏塔的建模及其非线性控制

黄江茵,赵 晶(厦门理工学院电气工程与自动化学院,福建厦门361024)



高纯度分馏塔的建模及其非线性控制

黄江茵*,赵 晶
(厦门理工学院电气工程与自动化学院,福建厦门361024)

摘要:以高纯度分馏塔为对象,研究其建模及控制策略.以变参数线性(LPV)动态模型结构为基础,分别对多项式权重和高斯权重进行改进.采用带约束的多项式权重,构造拉格朗日函数进行参数寻优,避免LPV模型增益符号的错误;将高斯函数改进为分段形式,使其能够应用于工作点非均匀分布的系统.分馏塔产品纯度输出拟合和阶跃响应曲线对比结果显示,基于上述2种权重函数的LPV模型均能够较好地拟合系统输出,最优匹配率达到74%以上,并符合实际对象阶跃响应特征.基于所建LPV模型设计非线性内模PID控制器,给出工作点上局部线性模型及控制器参数关系式,采用与辨识LPV模型时相同的方法对局部控制参数进行插值计算.仿真控制结果显示该方法能够有效地将2个输出控制在设定范围内,且具有参数整定简便,抗干扰性强的优点.

关键词:高纯度分馏塔;变参数线性模型;非线性PID控制

分馏塔是对混合挥发液体进行分馏的一种化工设备,是石油炼制企业中最常见的重要设备之一.高纯度分馏塔是典型的具有“病态、方向性”特征的非线性系统,对其进行辨识和控制一直是工业界和学术界的难点.当产品纯度接近100%时系统会进入饱和状态,产品的纯度越高,非线性程度越大[1].

由于分馏塔的运行原理明晰,大多数对分馏塔的建模研究都是根据物料平衡原理构建机理模型[2-3],但此类模型变量多,方程复杂,不适合用于实际工业系统的实时控制中.对分馏塔的先进控制方法,包括预测控制[4]、模糊PID控制[5]等,均基于近似线性模型,一定程度上影响了控制精度.若基于机理模型或者非线性模型,将大大增加优化计算的难度和耗费时间.本文采用改进权重函数的变参数线性(LPV)模型对高纯度分馏塔进行建模,提出非线性内模PID控制策略并进行仿真,获得了较好的输出拟合和控制效果.

1 高纯度分馏塔建模

1.1双操作LPV模型的改进

近年来LPV模型常被用于工业非线性系统的建模中[6].它的主旨思想是用一个基于“操作变量(scheduling variable)”的动态模型来表示非线性系统.该操作变量要求能够直接反映系统的运行特性.并且,其值可以实时测量,或者由其他变量计算得到,对于绝大多数工业系统,都可以找到符合上述条件的操作变量.式(1)是LPV模型的状态空间形式,w(t)是其操作变量,状态空间矩阵A,B,C,D都是w(t)的函数.

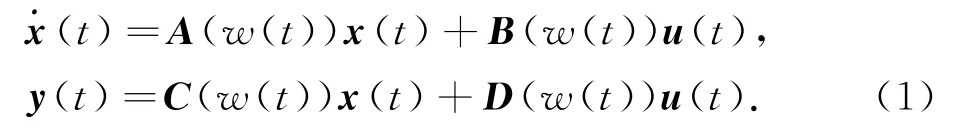
其中:x(t)为系统状态变量x(t)为其一阶导数;y(t)为系统输出;u(t)为系统输入.

LPV模型的辨识方法众多,包括正交基函数形式模型[7]辨识、传递函数形式模型[8]辨识等.大多数方法都采用极小化模型输出误差的方法进行参数优化,尽管能达到较好的拟合效果,却很难保证LPV模型的稳定性.原因在于难以确保整体模型的闭环特征根在w(t)的整个变化区间内始终处于复频域s左半平面.为克服此问题,Huang等[9]提出了一种基于局部线性模型插值的双操作变量LPV模型.以多输入单输出系统为例,定义w1(t)和w2(t)分别为系统的两个操作变量,假设该系统运行轨迹上共有n1×n2个相对稳态、对应的工作点,即操作变量值为:

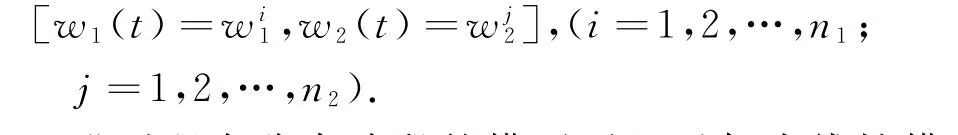
工业过程在稳态阶段的模型可以近似为线性模型,若上述工作点上,系统辨识得到的线性模型为

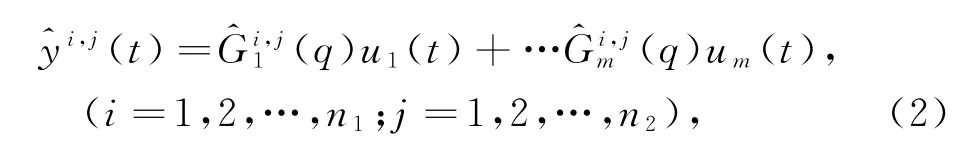
则LPV模型可由上述局部线性模型插值得到

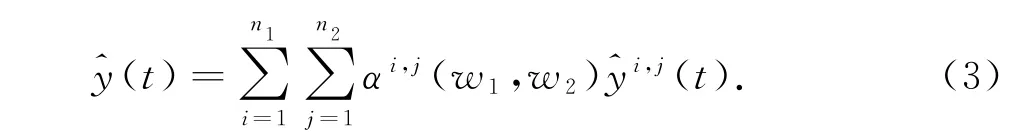
其中,模型权重αi,j(w1,w2)是关于两个操作变量的实函数.根据线性模型的叠加定义可知,式(3)采用的模型结构,只要局部模型稳定,整体LPV模型也稳定.局部模型可以采用传统的线性模型辨识方法获得.文献[9]中分别采用了线性、多项式和高斯函数进行了比对,并得出多项式权重由于无法保证权重值在[0, 1]范围内变化,虽然拟合误差可以很小,在阶跃响应上却可能出现增益符号错误的现象;高斯函数待定参数少,且能够通过归一化处理限制权重值,但高斯函数的对称性使其只能用于工作点均匀分布的对象中.针对多项式权重和高斯函数的局限性,可以对其分别作增加约束、分段优化的改进.

1.1.1带约束的多项式权重函数

以三阶多项式函数为例,双操作变量LPV模型权重函数可以表示为:

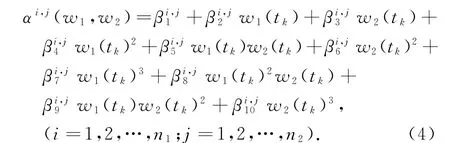
针对此问题,有必要在求解θ时,对权重值增加约束,即求解如下最优化方程:

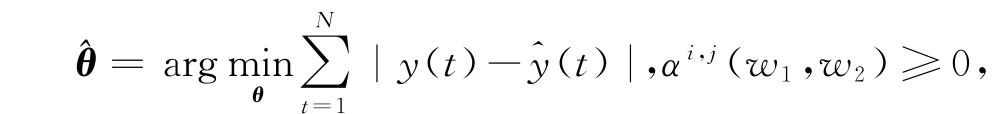
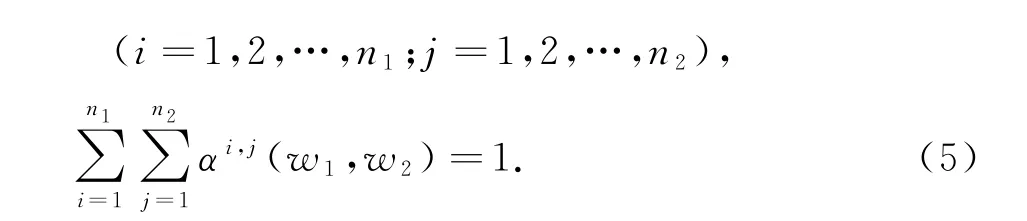
上述命题为带线性约束条件的线性规划问题,且同时含有等式和不等式约束.引入拉格朗日乘子和松弛因子,可将其改写为无约束问题进行求解.求解步骤如下:

1)引入(n1×n2)个松弛因子γi,j>0,将不等式约束αi,j(w1,w2)≥0改写为等效的等式约束-αi,j(w1,w2)+γ2i,j=0,(i=1,2,…,n1;j=1,2, …,n2);同时引入(n1×n2)个拉格朗日乘子λi,j作为上述等式约束的权重因子.

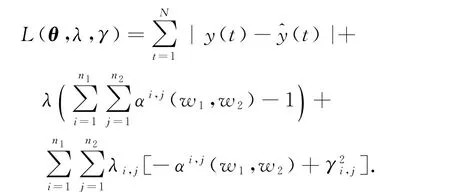
经过上述处理,已将式(5)中带约束条件的优化命题改写为无约束的线性规划问题,考虑待定参数与优化目标呈线性关系,可直接采用最小二乘法进行求解.

1.1.2分段高斯权重函数

传统高斯权重函数如下所示:

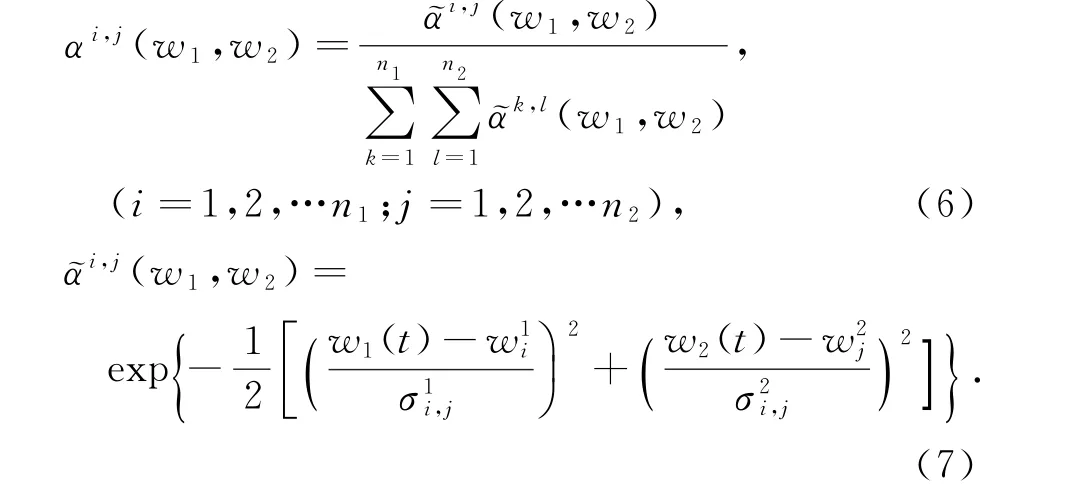
其中,σ1i,j和σ2i,j为分离系数,可简单地设定为相邻工作点之差的1/3,也可通过极小化输出误差寻优获得.

经过归一化处理,高斯权重值将在[0,1]范围内变化,保证了插值后LPV模型增益方向的正确性.但是,高斯函数图像本身具有对称性,要求建模对象的工作点均匀分布,这一缺陷使其在实际应用中存在较大局限.为解决此问题,可以将高斯函数沿着工作点写成分段函数,每一段用不同的分离系数,即将式(7)改写为:

若希望进一步提高LPV模型的拟合精度,也可沿用极小化输出误差,采用牛顿法、最速下降法等寻优计算各分离系数.

1.2高纯度分馏塔模型LPV模型辨识

高纯度分馏塔有很多简化机理模型,其中最为经典的为Skogestad提出的回流-再沸(LV)运行模式模型[10],该模型以其模型准确、仿真简便,广泛地用于高纯度分馏塔建模和控制研究[11-12].LV运行模式中,两个操作变量分别为回流速度vLT和再沸器流速vVB;两个被控变量分别是顶部产品纯度wD和底部产品杂质wB;同时有3个干扰变量:进料速度vF、进料中轻组分的摩尔分数xF,以及进料纯度wF.Skogestad已将该机理模型形成MATLAB文件并公开化,用户可直接下载,进行仿真和相关研究.图1为该模型结构简图.

通过对高纯度分馏塔仿真模型的阶跃响应测试,结合参考文献对该模型运行特性的介绍,可知进料速度vF的改变是激发分馏塔非线性特性的重要因素,另外,顶部产品纯度wD是生产过程中最重要的质量评价指标.因此,先选择vF和wD作为LPV模型的2个操作变量.为简化模型,xF和wF维持恒值不变.模型的控制变量(输入)为vLT,vB;被控变量(输出)为wD,wB;扰动变量为vF.

图1　高纯度分馏塔LV运行模型示意图Fig.1 LV model structure of high purity distillation column

仿真辨识过程共选择5×3=15个局部稳态工作点,由于vF的改变对系统运行影响较大,在vF上选择了均匀分布的5个工作点;考虑到随着wD的纯度升高,系统的非线性程度也变得越明显,在wD上选择3个非等间隔的工作点.15个工作点上对应的操作变量值vF分别为0.8,0.9,1.0,1.1,1.2;wD分别为95%, 98%,99%.

系统在其中6个工作点上的阶跃响应曲线如图2所示.从图中可以看出,系统在各个工作点上的阶跃响应曲线增益方向相同,但幅值却有较大差别.这2个特点使采用基于局部线性模型插值的LPV模型对高纯度分馏塔进行建模成为可能.

辨识实验共进行50 000 min,采样时间为1 min.假设实验过程中vF和wD的变化轨迹如图3所示.

辨识数据采集过程中,控制器未工作.为获得包含较多系统特性的辨识数据,输入端vLT和vVB上叠加上了广义二进制噪声(GBN)实验信号[13],信号的转换时间为50 min.同时,为了模拟实际工业系统在运行中的可测和不可测扰动,分别在输入和输出端叠加了如下扰动:

1)输入vF上叠加滤波白噪声序列,幅值为GBN信号的30%,滤波器为1/(1-0.8q-1)(q-1为单位延迟算子).辨识实验过程中,该信号作为扰动叠加在vF上,但辨识时不进行采集,用来模拟vF上的不可测噪声.

2)输出wB和wD上分别叠加波动幅度为1%的白噪声信号,并进行采集,模拟系统输出端的可测噪声.

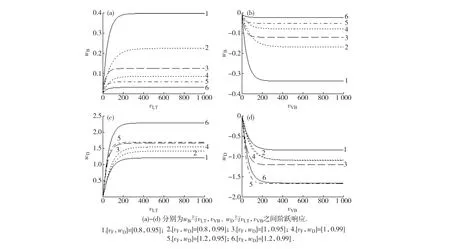
图2　工作点处实际系统阶跃响应曲线Fig.2 Step responses of the real process at working points

图3　操作变量vF和wD的变化轨迹Fig.3 Trajectory of the scheduling variables vFand wD

图4　辨识实验数据Fig.4 Identification test data set

wD既是系统操作变量,又是输出变量.在实验过程中由于叠加了扰动信号、GBN信号,导致wD实际数据与图2设计的轨迹略有区别,但并不影响后续的辨识算法.辨识实验采集到的数据如图4所示.

文献[14-15]采用最大期望算法,以模型权重作为隐藏变量,迭代期望值以估计最大似然函数,从而同时对局部线性模型参数及权重参数进行寻优.该方法优势在于无需对局部模型动态特征有充分了解,可直接从系统的输入输出数据构建LPV模型.首先尝试用该方法对高纯度分馏塔进行建模.实验获得了较好的输出拟合结果,但所获的15个局部线性模型中,有8个出现不稳定现象.究其原因,该算法在迭代时未考虑局部模型特征根变化趋势,导致出现输出误差小,模型却不稳定的情况.由此可见,工业非线性系统建模是一个十分复杂的过程,衡量非线性系统建模算法是否有效,除了对输出拟合做评价外,还需验证在典型工作点处,所建模型是否符合实际对象动态特征.

采用本文提出的算法进行LPV模型辨识,分别截取各工作点附近的数据,用渐进辨识法[16]获得局部线性模型,再分别采用带约束的多项式权重以及分段高斯权重,对上述15组线性模型进行插值计算,构造整体LPV模型.图5为15个工作点上各线性模型的分段高斯权重.图中可看出,所有的权重值均在[0,1]范围内,且呈规律性变化,在每一个工作点处,其对应局部线性模型的权重达到峰值1,随着操作变量渐渐偏离工作点,该权重值则平稳减小,直至等于0.

图5　分段高斯权重Fig.5 Segmented Gaussian weights

系统实际输出和LPV模型输出对比如图6,7所示.带约束多项式权重LPV模型的最优匹配率p为wB:84.2%,wD:91.7%;分段高斯权重LPV模型的p分别为wB:78.6%,wD:89.4%.可看出多项式权重获得略高的输出拟合精度.[wF,wD]=[0.85, 0.96]时实际系统和LPV模型的阶跃响应如图8所示.从图6～8可以看出,2种权重的LPV模型都获得了较好的输出拟合度,阶跃响应曲线也与实际系统较为吻合.

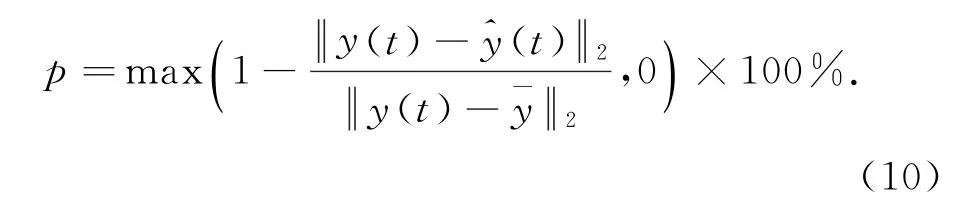
2 高纯度分馏塔控制

2.1基于LPV模型的非线性内模PID控制

虽然LPV模型的辨识方法的研究层出不穷,但是针对该模型的先进控制算法却较少人涉猎.原因一方面在于LPV模型的非线性时变特性,大大增加了先进控制算法中预估系统输出以及控制约束方程的寻优难度[17],时常无法获得局部收敛的最优解;另一方面,复杂的寻优方法需耗费较长的求解时间,在实际应用时不符合实时控制要求.针对此问题,本文利用PID控制器鲁棒性强、参数个数少、整定方便等显著优点,采用非线性内模PID策略,对高纯度分馏塔进行控制仿真.首先基于辨识得到的局部线性模型推知局部内模控制器参数,随后以建模时相同的操作变量为自变量,构建权重函数对局部PID参数进行插值,使控制参数在整个操作轨迹上实现动态平滑过渡,获得较好的控制效果.

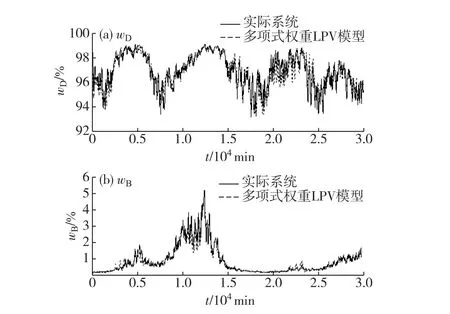
图6　实际系统输出和多项式权重LPV模型输出对比Fig.6 Comparison of the outputs of real process and LPV model with polynomial weight

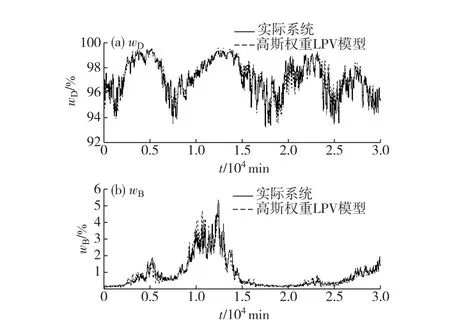
图7　实际系统输出和高斯权重LPV模型输出对比Fig.7 Outputs of real process and LPV model with Gaussian weight

内模控制(internal model control,IMC)是基于过程的数学模型进行控制器设计的控制策略.该控制器由内模控制器以及过程模型构成,其等效传递函数为:

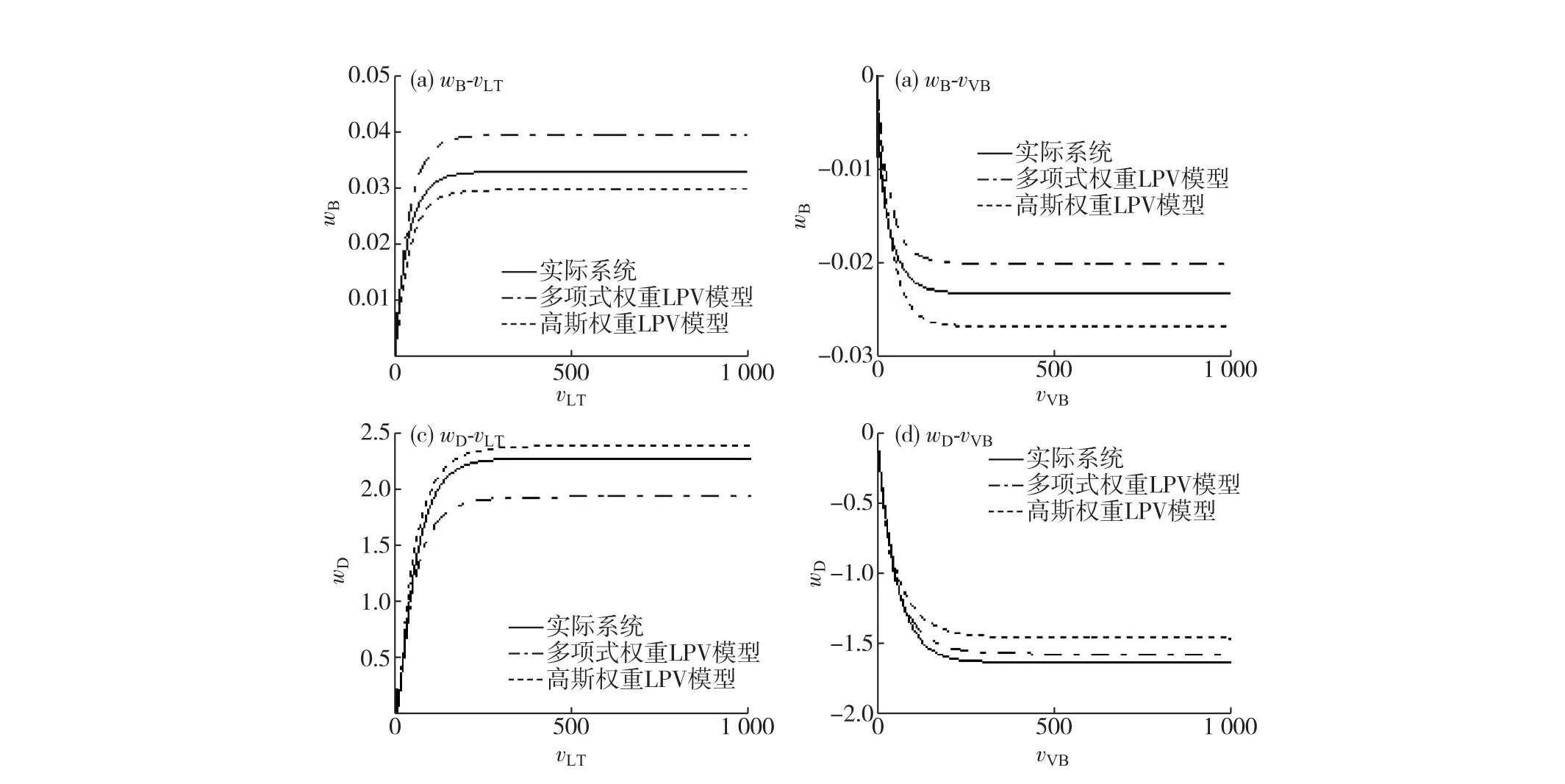
图8　[vF,wD]=[0.85,0.96]时实际系统和LPV模型阶跃响应对比Fig.8 Step responses of real process and LPV model at[vF,wD]=[0.85,0.96]

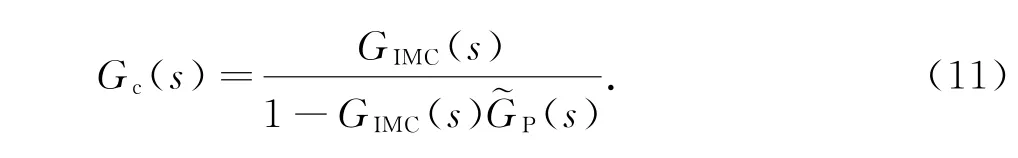
其中,GIMC(s)为内模控制器,GP(s)为被控对象辨识模型.进行控制器设计时,首先将GP(s)分解为全通部分和最小相位部分,GIMC(s)由最小相位部分和一低通滤波器串联而成.低通滤波器参数为唯一需设计的参数[18].

第1.2节辨识得到了分馏塔15个工作点上的局部线性模型.假设各模型具有相同的滞后环节,且可近似表示为如下一阶形式:

首先将滞后环节进行一阶Pade近似,即

将式(12),(13)代入式(11),并用一阶滤波器F(s)=整理化简得各工作点上的局部控制器传递函数为:

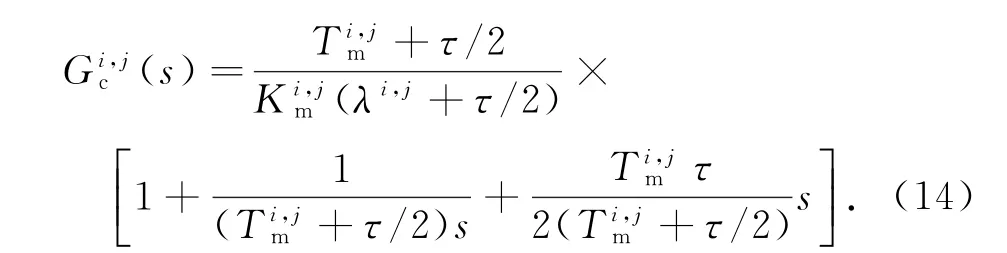
其中下标P,I,D的含义分别对应于比例、积分、微分.

与第1.2节中辨识LPV模型的思路相同,以双操作变量为例,基于LPV模型的非线性内模PID控制可以通过下列步骤完成:

1)在系统的各个稳态阶段,整定内模PID控制器的局部参数λi,j并根据公式(15)计算(i=1,2,…,n1;j=1,2,…,n2).

2)以选定的操作变量为自变量,设计函数计算各局部控制参数的权重,插值后获得基于LPV模型的非线性PID控制器参数.

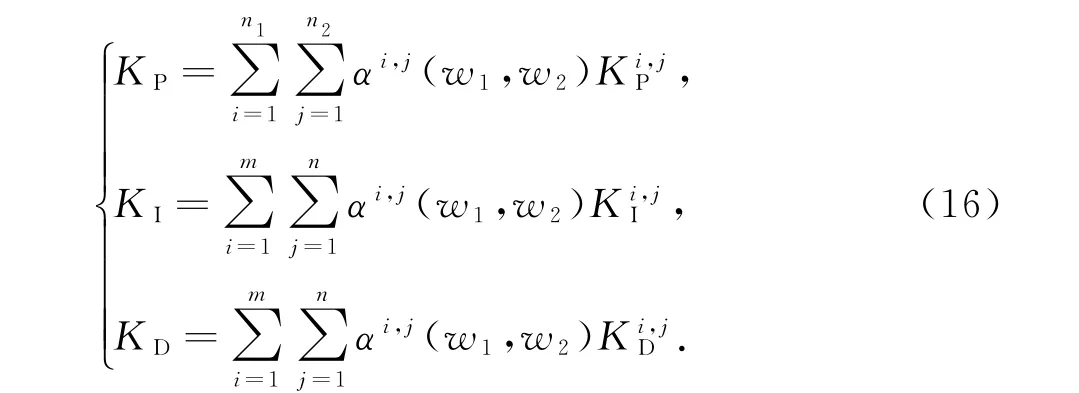
其中αi,j(w1,w2)是以w1(t)和w2(t)为自变量的归一化权重函数.权重函数同样可以采用线性函数、高斯函数以及多项式函数等常见的拟合函数.除了线性函数以外,高斯、多项式函数中均含有待定参数,可以通过最速下降法求解如下输出极小化问题进行寻优:

其中,r(t)为设定值,y(t)为闭环系统输出,u(t)为非线性PID控制器输出,(s,w1,w2)为被控对象LPV模型,N为样本空间容量.

2.2高纯度分馏塔控制仿真

基于第1.2节中获得的LPV模型,对高纯度分馏塔进行非线性内模PID控制仿真.vLT主要用于保证wB尽量接近0;vVB则用于控制wD使其保持较高精度.首先通过辨识得到的局部线性模型,整定15组工作点上的一阶滤波器参数λi,j,后根据式(16)进行插值计算非线性PID控制器参数.控制仿真共进行5 000 min,采样时间为1 min.与第1.2节相同,输入vF变化范围为0.8～1.2 kmol/min,并叠加了不可测扰动信号,输出wD和wB端上叠加可测扰动信号.两个非线性PID控制器分别通过调整vLT和vVB,使产品wD和wB保持在较高的纯度上.wB的设定值为99%,wB的设定值为1%.图9对比了传统PID以及非线性内模PID的仿真控制结果.从图中可以看出,传统PID控制器参数恒定,无法适应分馏塔整个运行轨迹.随着vF的变化2个输出都出现了偏离设定值的现象;而采用本节提出的非线性内模PID控制算法则能够使2个输出都在设定值附近波动,获得了较好的控制效果.

3 结 论

本文主要研究高纯度分馏塔这一典型非线性工业系统的建模和控制.选择vF和wD作为操作变量,分别采用基于改进的多项式和高斯权重的LPV模型对其进行建模.对传统多项式权重函数增加约束以限制权重值大小,引入拉格朗日乘子将约束优化命题转为无约束优化,进行参数寻优计算;将高斯函数写为分段形式,使LPV模型能够用于工作点非均匀分布的建模对象.通过比较实际系统和LPV模型的输出以及阶跃响应曲线,证实2种改进权重后的LPV模型不仅能够获得较好的拟合效果,同时也可以保证阶跃响应与实际系统吻合,克服了传统多项式权重LPV模型增益符号容易出错的缺点.设计基于LPV模型的非线性内模PID控制器,给出局部模型与内模PID控制参数关系式.首先整定局部滤波器参数,计算局部控制参数后进行插值,获得整体非线性PID控制器参数.仿真控制结果表明该控制方法能够将高纯度分馏塔的2个产品都控制在较高的纯度范围内,达到了良好的控制效果.

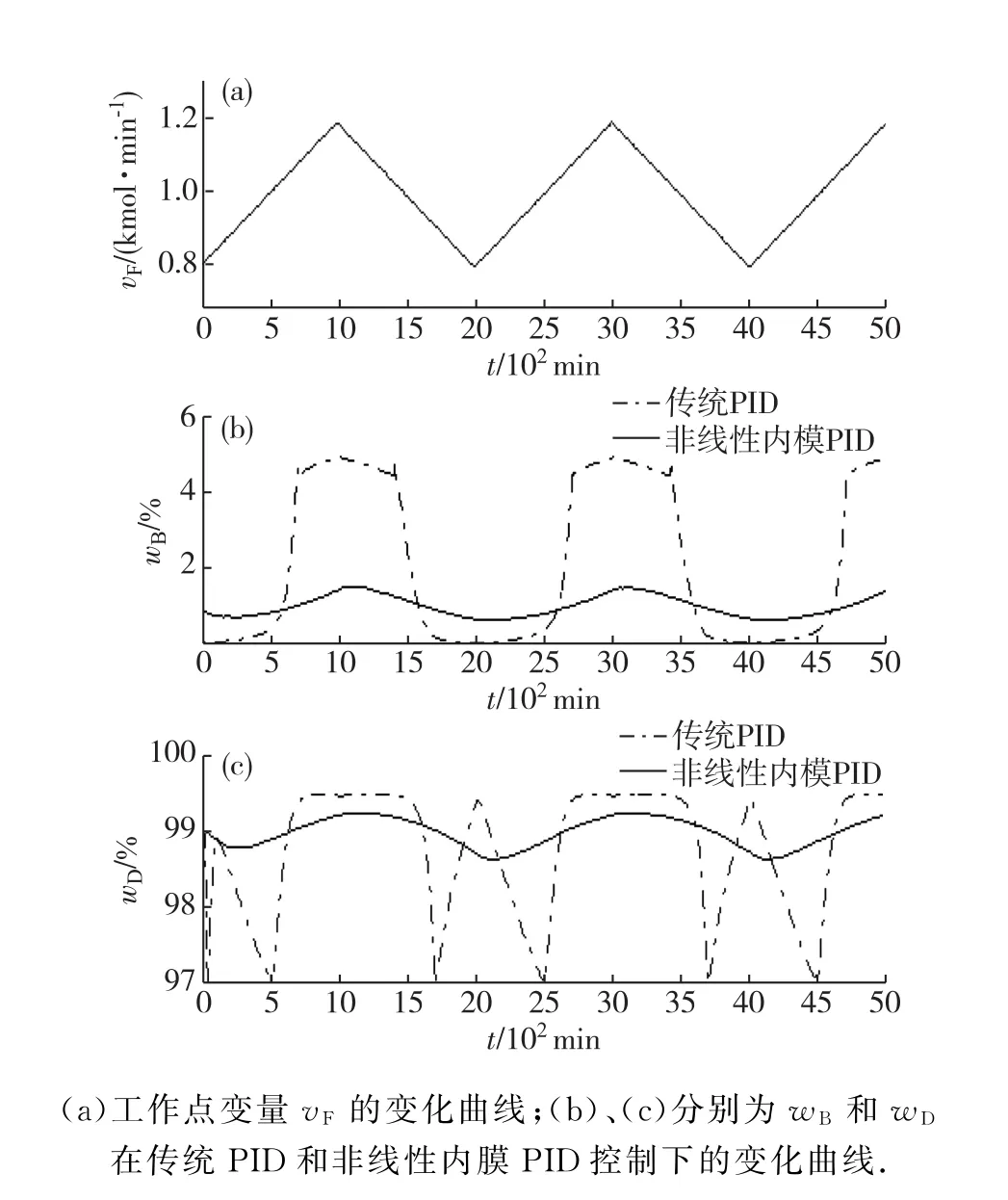
图9　传统PID及非线性内模PID控制效果对比Fig.9 Control efforts comparison of traditional and IMC nonlinear PID controller

参考文献:

[1] LINHART A,SKOGESTAD S.Reduced distillation models via stage aggregation[J].Chemical Engineering Science,2010,65(11):3439-3456.

[2] 侯颍,张贝克,马昕.三元物系共沸精馏塔建模与仿真[J].计算机仿真,2014,31(1):247-252.

[3] 樊少冬,张金桥,谢贤金,等.含氮天然气液化脱氮精馏塔液位控制模型和仿真[J].自动化与仪器仪表,2015,175 (5):187-190.

[4] 何仁初,印大伟,侯明辉,等.基于MATLAB/Simulink的乙烯精馏塔多变量预测控制仿真研究[J].工业控制与应用,2014,33(5):37-43

[5] 潘海鹏,杨兆海,任佳.模糊自调整PID的精馏塔参考模型解耦控制研究[J].计算机与应用化学,2011,28(7): 851-854.

[6] HUANG J Y,JI G L,ZHU Y C.Identification and MPCcontrol of a circulation fluidized bed boiler using an LPV model[C]∥Proceeding of the 9th International Symposium on Dynamics and Control of Process Systems. Belgium:IFAC,2010:853-858.

[7] ROLAND T,HEUBERGER P S C,VAN DEN HOF P M J.Asymptotically optimal orthonormal basis functions for LPV system identification[J].Automatica,2009,45 (6):1359-1370.

[8] LAURAIN V,GILSON M,TOTH R,et al.Refined instrumental variable methods for identification of LPV Box-Jenkins models [J].Automatica,2010,46(6): 959-967.

[9] HUANG J Y,JI G L,ZHU Y C,et al.Identification of

multi-model LPV models with two scheduling variables

[J].Journal of Process Control,2012,22(7):1198-1208. [10] SKOGESTAD S.Dynamics and control of distillation columns:a tutorial introduction[J].Chemical Engineering Research and Design,1997,75(6):539-562.

[11] BACHNAS A A,TOTH R,LUDLAGE J H A,et al.A

review on data-driven linear parameter-varying modeling approaches:a high-purity distillation column case study [J].Journal of Process Control,2014,24(4):272-285. [12] BISWAS P P,RAY S,SAMANTA A N.Nolinear control of high purity distillation column under input saturation and parametric uncertainty[J].Journal of Process Control,2009,19(1):75-84.

[13] LJUNG L.System identification:theory for the user [M].Upper Saddle River:Prentice-Hall,NJ,1987: 834-835.

[14] CHEN L,ADITYA T,HUANG B,et al.Multiple model approach to nonlinear system identification with an uncertain scheduling variable using EM algorithm [J]. Journal of Process Control,2013,23(10):1480-1496.

[15] JIN X,HUANG B,SHOOK D S.Multiple model LPV approach to nonlinear process identification with EM algorithm[J].Journal of Process Control,2011,21(1): 182-193.

[16] ZHU Y C.Multivariable system identification for process control[M].London:Elsevier Science,2001: 183-196.

[17] PARK J H,KIM T H,SUGIE T.Output feedback model predictive control for LPV systems based on quasi-min-max algorithm[J].Automatica,2011,47(9): 2052-2058.

[18] 刘红军,韩璞,孙海蓉,等.基于内模控制的PID控制器的设计[J].计算机仿真,2004,22(3):207-210.

Modeling and Nonlinear Control for a High Purity Distillation Column

HUANG Jiangyin*,ZHAO Jing
(School of Electrical Engineering and Automation,Xiamen University of Technology,Xiamen 361024,China)

Abstract:This paper studies the modeling and control strategy for a high purity distillation column,which involves a complex nonlinear industrial process.The linear-varying-parameter(LPV)models based on polynomial and Gaussian weight are improved.A constrained polynomial function is used to avoid sign errors in LPV model's gain.Parameters are estimated by Lagrange method.The LPV model with segmented Gaussian function can be used in the system which contains non-uniform distribution working points. Comparisons of the distillation column's outputs and step response curves show that both LPV models with polynomial and Gaussian weighting function can obtain good fittings of process outputs and step responses,with all best fit percentage being greater than 74%. Nonlinear IMC based PID controller based on LPV model is also developed.The relations between local models and control parameters are derived,and then control parameters are interpolated as the same way as LPV model.The results of simulation control show the proposed method achieves good control effects with respect to small output errors,and enjoys the advantage of simple tuning and anti-interference abilities.

Key words:high purity distillation column;linear parameter varying(LPV)model;nonlinear PID control

*通信作者:jiangyinhuang@xmut.edu.cn

基金项目:福建省自然科学基金(2015J01275);厦门理工学院对外科技合作与交流专项(E201400900,E201401400)

收稿日期:2015-04-23 录用日期:2015-07-23

doi:10.6043/j.issn.0438-0479.2016.02.018

中图分类号:TP 273

文献标志码:A

文章编号:0438-0479(2016)02-0251-08

引文格式:黄江茵,赵晶.高纯度分馏塔的建模及其非线性控制[J].厦门大学学报(自然科学版),2016,55(2):251-258.

Citation:HUANG J Y,ZHAO J.Modeling and nonlinear control for a high purity distillation column[J].Journal of Xiamen University(Natural Science),2016,55(2):251-258.(in Chinese)