联图的Normalized Laplace特征多项式

廖丽雯,陈海燕(集美大学理学院,福建厦门361021)



联图的Normalized Laplace特征多项式

廖丽雯,陈海燕*
(集美大学理学院,福建厦门361021)

摘要:利用代数方法得到了两个正则图联图的Normalized Laplace特征多项式的一个表达式,在此基础上得到了正则图联图的Normalized Laplace特征值与其因子图对应特征值之间的关系式.计算了一些特殊图的度基尔霍夫指标.

关键词:联图;Normalized Laplace多项式;度基尔霍夫指标

设G是一个n个顶点的简单图,它的顶点集为{1,2,…,n},则G的邻接矩阵是一个(0,1)矩阵,记为A=(aij)n×n,其中

图G的Normalized Laplace矩阵和图G上的随机游动有紧密的联系,它的许多性质已被人们所熟知,如

1)L是半正定矩阵;

2)0是L的特征值,且它的所有特征值位于闭区间[0,2].

其他更多性质可参见文献[1].

设图G邻接矩阵特征值与Normalized Laplace特征值分别为λ1≥λ2≥…≥λn,0≤λ'2≤…≤λ'n.如果G为r-正则图,则由定义直接可得:

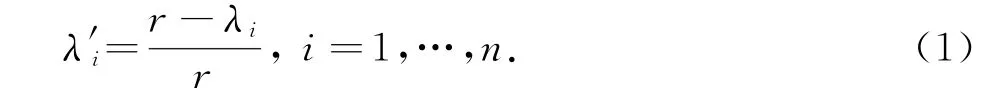
但如果G不是正则图,λi和λ'i之间就没有必然的联系.本文我们主要考虑两个图联图的Normalized Laplace特征值与其因子图Normalized Laplace特征值的关系.首先我们给出联图的定义.

定义1[2]设H与G是两个简单连通图,则它们的联图记为H∇G,是指顶点集为V(H)∪V(G),边集为E(H)∪E(G)∪{uv|u∈V(H),v∈V(G)}的图.

下面我们用χ(G;x)表示图G的Normalized Laplace特征多项式,则

在第二部分,首先用代数方法得到了两个正则图联图的Normalized Laplace多项式的一个表达式,然后在此基础上得到了两个正则图联图的Normalized Laplace特征值和其两个因子图Normalized Laplace特征值之间的关系式.第三部分作为应用,得到了一些特殊图的度基尔霍夫指标的表达式.

1 正则图联图的Normalized Laplace多项式

为了讨论正则图联图的Normalized Laplace特征多项式,需要下面的已知结论:

引理1[3]设A,B是两个n阶对称矩阵,若AB=BA,则存在可逆矩阵P,使得

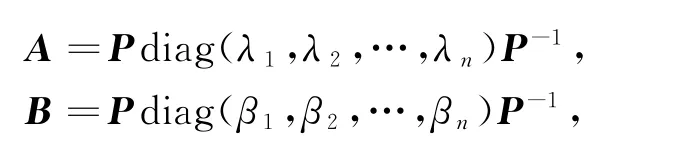
这里λi,βi分别表示A,B的特征值,即

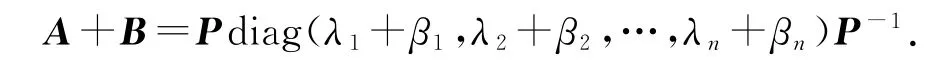
定理1 设G1,G2是两个正则图,顶点数分别为n1,n2,正则度分别为r1,r2.则联图G1∇G2的Normalized Laplace特征多项式为:

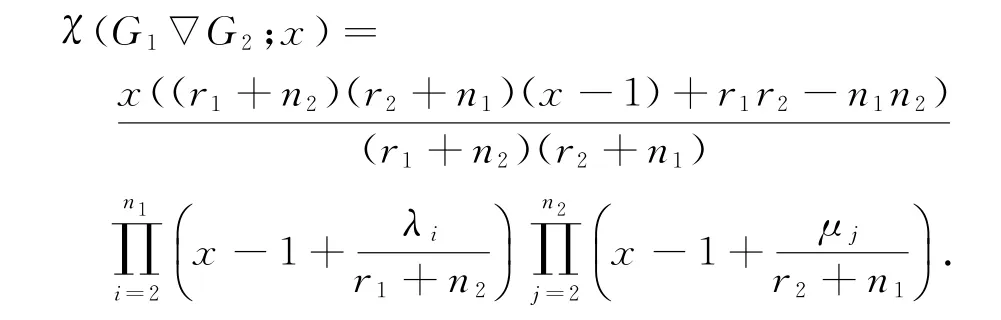
这里r1≥λ2≥…≥λn1,r2≥μ2≥…≥μn2分别是G1和G2邻接矩阵的特征值.

证明 用A1,A2分别表示G1,G2的邻接矩阵,则由联图的定义可得G1∇G2的邻接矩阵和度对角矩阵可分别表示为:

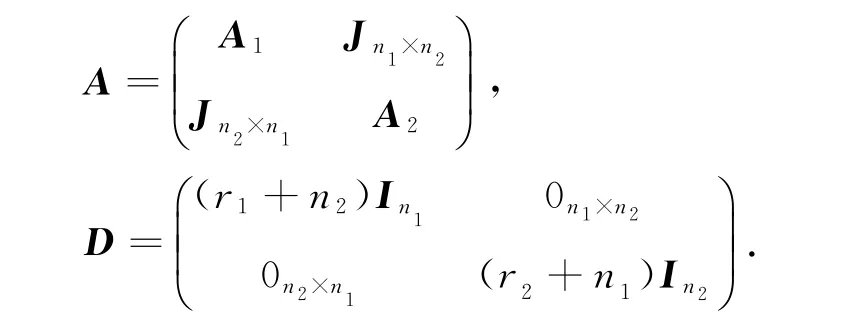
所以

从而可得

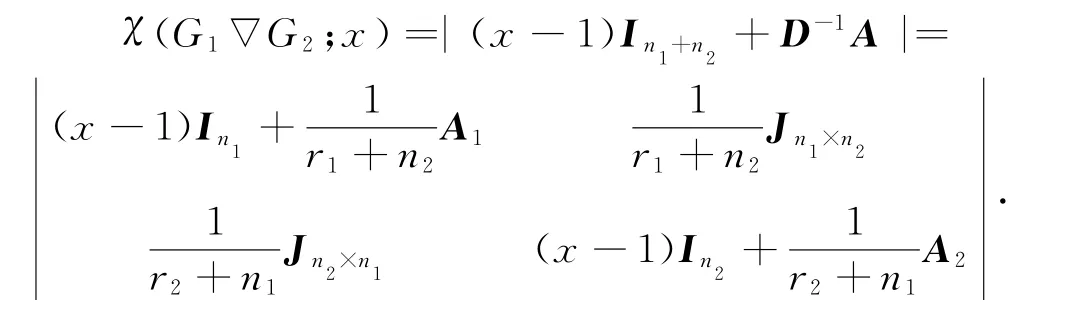
由于G1是r1正则图,所以Jn2×n1A1=r1Jn2×n1.把上面的行列式第一行左乘矩阵

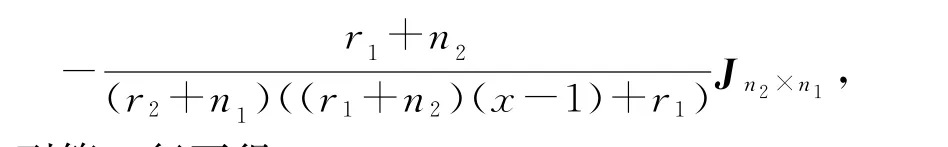
加到第二行可得

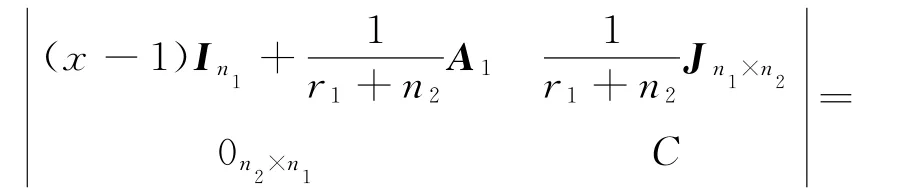
这里

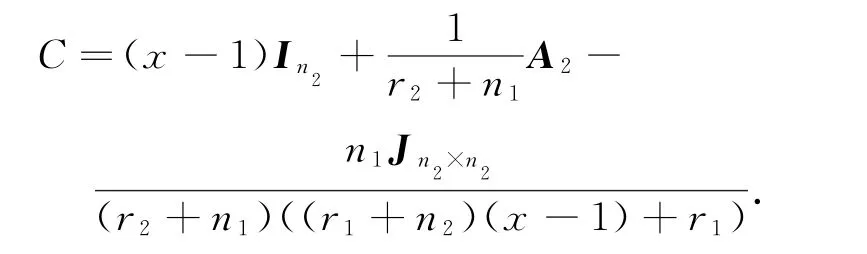
设A1的特征值为r1≥λ2≥…≥λn1,则显然有

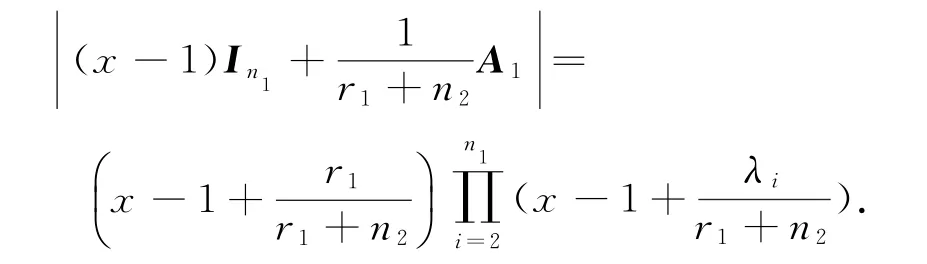
又G2是r2正则图,A2Jn2×n2=Jn2×n2A2=r2Jn2×n2,若设r2≥μ2≥…≥μn2为A2的特征值,Jn2×n2的特征值为n2,0,…,0,则由引理1可得:

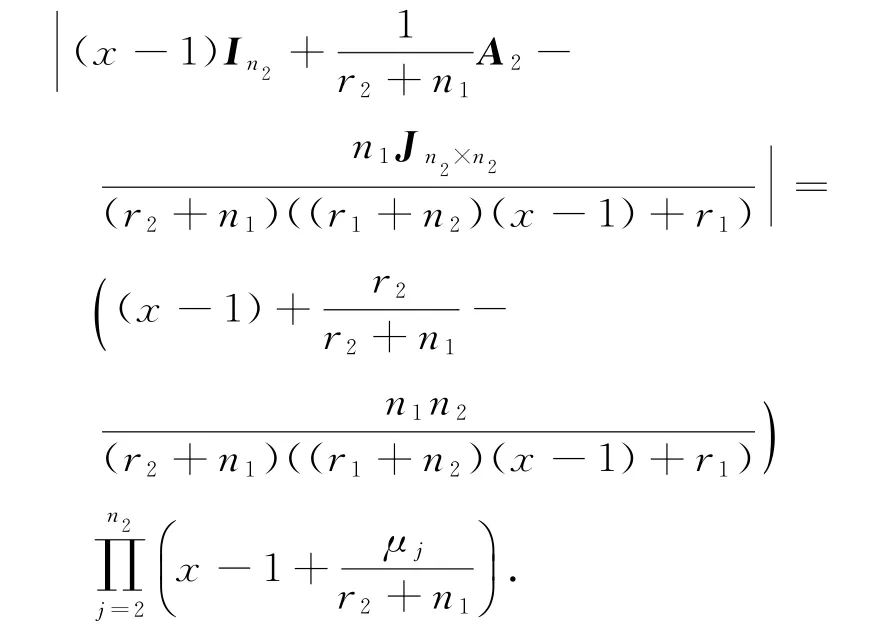
由上得G1∇G2的Normalized Laplace特征多项式为:

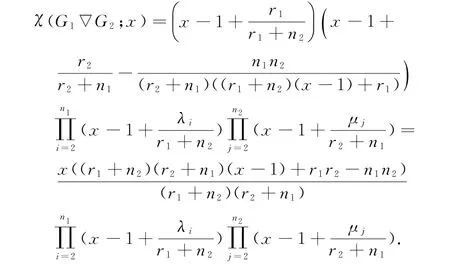
由上面的定理,我们很容易由G1,G2的邻接矩阵特征值得到G1∇G2的Normalized Laplace特征值:

再由正则图的邻接矩阵特征值和其Normalized Laplace特征值之间的关系(1),我们马上可以得到下面的定理.

定理2 设G1,G2是两个正则图,顶点数分别为n1,n2,正则度分别为r1,r2.若G1的Normalized Laplace特征值为0≤λ'2≤…≤λ'n1;G2的Normalized Laplace特征值为0≤μ'2≤…≤μ'n2,则联图G1∇G2的Normalized Laplace特征值为:

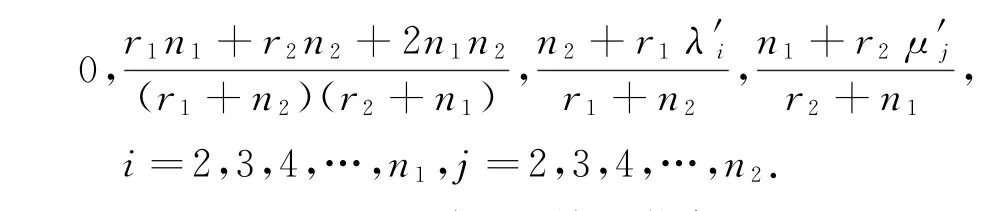
这里G1,G2是正则图,并不能保证G1∇G2是正则图,除非r1+n2=r2+n1,所以定理2的结果并不能通过式(1)由G1∇G2邻接特征值与G1和G2邻接特征值的关系得到.

推论1 设G1,G2是两个正则图.若1作为它们Normalized Laplace特征值的重数分别为m1,m2,则1作为G1∇G2的Normalized Laplace特征值的重数为m1+m2.

在定理1中,若特别取其中一个图为空图஀Km或完全图Km,由于஀Km的正则度和所有特征值都为0, 而Km是m-1正则,特征值为m-1,-1,-1,…, -1,所以可以得到下面更具体的结果.

推论2 设图G是n个顶点的r正则图,则

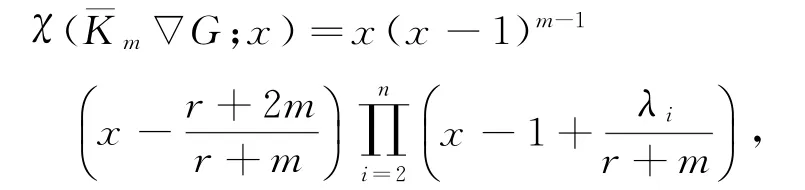
这里r≥λ2≥…≥λn是G的邻接矩阵特征值.所以஀Km∇G的Normalized Laplace特征值为:

推论3 设图G是n个顶点的r正则图,则

χ(Km∇G;x)=

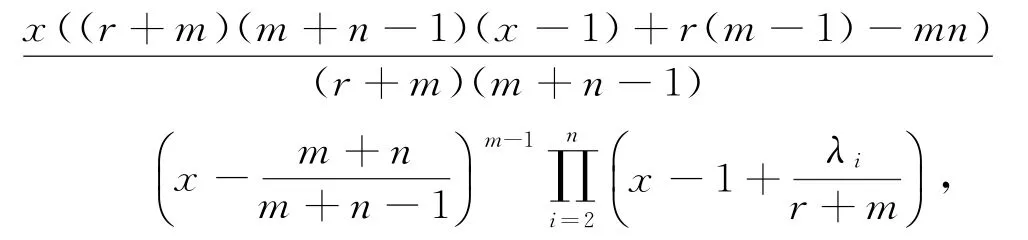
这里r≥λ2≥…≥λn是G的邻接矩阵特征值.所以Km∇G的Normalized Laplace特征值为:

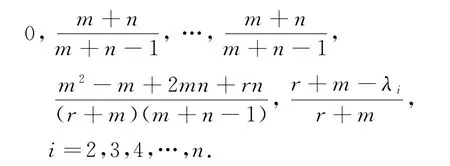
2　应 用

设G是一个简单连通图,若G的每条边看作电阻值为1的电阻,则G就可以看作是一个电网络.Klein 和Randic在文献[4]中把图G上两点i,j之间的电阻距离定义为它们之间的等效电阻值,记为rij,而G中所有点对之间的电阻距离之和,即Kf(G)称为图G的基尔霍夫指标.而最近,Chen等在文献[5]中定义了度基尔霍夫指标:并发现Kf*(G)和图的Normalized Laplace特征值有如下的关系式.

引理2[5]设图G=(V(G),E(G)),其中|V(G)| =v,|E(G)|=e,则有

其中σ2≥σ3≥…≥σn是G的非零Normalized Laplace特征值.

由上面的引理和式(2),马上可得到两个正则图联图的度基尔霍夫指标的一个表达式.

定理3 设G1,G2是两个正则图,顶点数分别为n1,n2,正则度分别为r1,r2.则

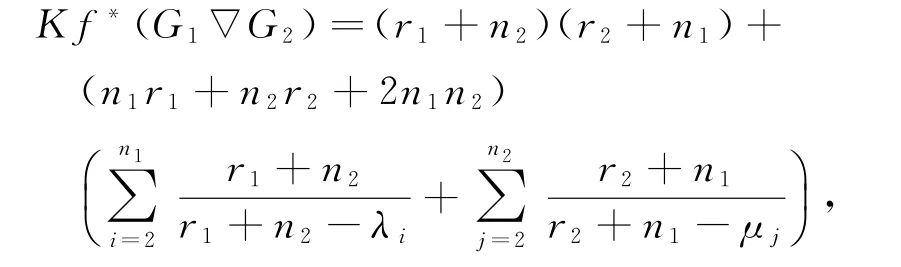
这里r1≥λ2≥…≥λn1,r2≥μ2≥…≥μn2分别是G1和G2邻接矩阵的特征值.

特别地,若G是一个正则图,则它的锥图(K1∇G)和双锥图(஀K2∇G)的度基尔霍夫指标有如下结果.

定理4 设G是n个顶点r-正则的图,则这里r≥λ2≥…≥λn是G的邻接矩阵特征值.

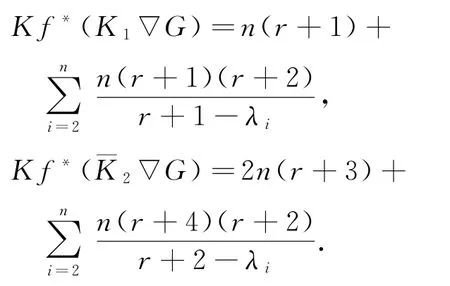
这里r≥λ2≥…≥λn是G的邻接矩阵特征值.

最后我们给出几类常见正则图联图的度基尔霍夫指标.

例1 图஀Km∇Kn的度基尔霍夫指标.

因为஀Km的正则度和所有特征值都为0,而Km是m-1正则,特征值为m-1,-1,-1,…,-1的图,所以由定理3马上可得:

例2 图஀Km∇Cn的度基尔霍夫指标.

Cn的邻接矩阵特征值为[6]:

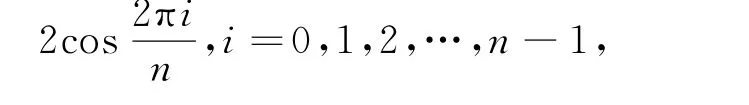
所以由定理3可得

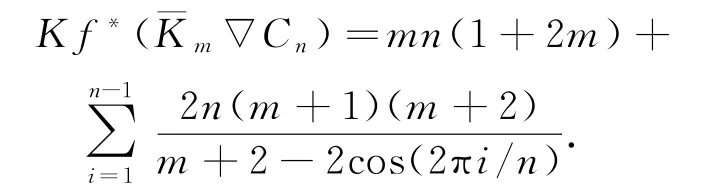
特别对于轮图,有

例3 图Km∇Cn的度基尔霍夫指标

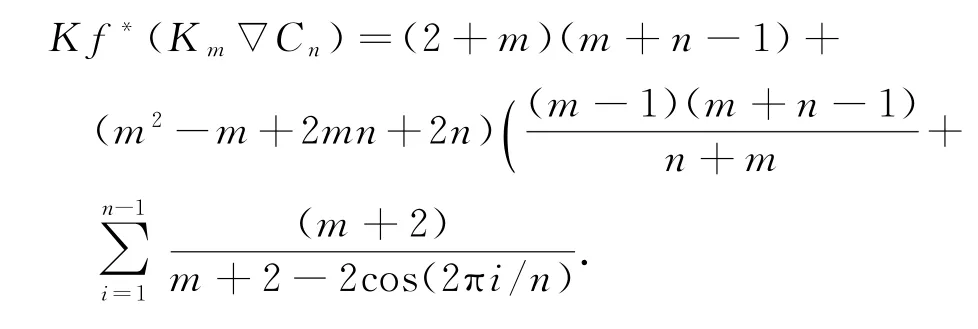
例4 图Km∇O3(O3是Peterson图)的度基尔霍夫指标.

Petersen图的邻接矩阵特征值为[2]:

3,1,1,1,1,1,-2,-2,-2,-2.

所以

参考文献:

[1] CHUNG F R K.Spectral graph theory[M].Rhode Island: Amer Math Soc,1997:186-199.

[2] CVETKOVIC'D,ROWLINSON P,SIMIC'S.An introduction to the theory of graph spectra[M].New York: Cambridge University,2010:1-23.

[3] MARCUS M,MINC H.A survey of matrix and matrix inequalities[M].Boston:Allyn and Bacon Inc,1964: 156-167.

[4] KLEIN D J,RANDIC'M.Resistance distance[J].Math Chem,1993,12(1):81-95.

[5] CHEN H Y,ZHANG F J.Resistance distance and the normalized laplacian spectrum[J].Discrete Applied Mathematics,2007,155:654-661.

[6] BIGGS N L.Algebraic graph theory[M].2nd ed.New York:Cambridge University,1993:14-22.

Normalized Laplace Polynomials of Join Graphs

LIAO Liwen,CHEN Haiyan
(School of Sciences,Jimei University,Xiamen 361021,China)

Abstract:Let G1and G2be two regular graphs.In this paper,by using algebraic method,we first obtain an expression of the Normalized Laplace polynomial for the join graph of G1and G2.Then based on this expression,we obtain the relation between the normalized Laplace eigenvalues of the join graph and those of G1and G2.Finally,as applications,we compute the degree Kirchhoff index of several kinds of graphs.

Key words:join graph;normalized laplace polynomial;degree Kirchhoff index

*通信作者:chey5@jmu.edu.cn

收稿日期:2015-05-13 录用日期:2015-08-26

doi:10.6043/j.issn.0438-0479.2016.02.015

中图分类号:O 157.1

文献标志码:A

文章编号:0438-0479(2016)02-0233-04

引文格式:廖丽雯,陈海燕.联图的Normalized Laplace特征多项式[J].厦门大学学报(自然科学版),2016,55(2):233-236.

Citation:LIAO L W,CHEN H Y.Normalized Laplace polynomials of join graphs[J].Journal of Xiamen University(Natural Science),2016,55(2):233-236.(in Chinese)