一类三维Hopf流形上全纯线丛的Hodge数

甘 宁(集美大学理学院,福建厦门361021)



一类三维Hopf流形上全纯线丛的Hodge数

甘 宁
(集美大学理学院,福建厦门361021)

摘要:设X是一个三维的主Hopf流形C3-{0}/,这里g是一个非对角的收缩.利用Douady序列及群作用的方法,计算了X上全纯线丛的上同调群的Hodge数.这些结果将有助于研究非代数流形上线丛的结构.

关键词:Hopf流形;上同调;全纯线丛;Hodge数

非代数流形上的向量丛是多复变及复几何研究中的一个热点,具体一些结果可参见文献[1-2]. Hopf流形是一类简单但却很重要的紧的非Kähler流形,Mall在文献[3]中研究了主Hopf流形上的全纯线丛,并给出了主Hopf曲面及对角型的主Hopf流形上全纯线丛的Hodge数的计算公式,对于一般的非主Hopf流形上的相应结果可参阅文献[4-5].在这篇文章中我们运用了文献[3]中的Douady序列并利用群作用的方法给出了一类非对角的三维主hopf流形上全纯线丛Hodge数的计算公式.这些结果在研究三维Hopf流形的几何性质中有重要的应用[6-7].

1 Hopf曲面,平坦线丛,Douady序列

Hopf流形是一个紧复流形,其万有覆盖空间双全纯等价于W,这里W=Cn-{0}.Hopf流形X具有商空间的形式W/G,G是W→W的一个自同构群,G作用在W上是真不连续以及固定点自由的,π:W→X=W/G为典范的投影,X的基本群π1(X)≅G.当G是无限循环群时,X称为主Hopf流形,否则称为第2类或者非主Hopf流形.

我们称映射f:(Cn,0)→(Cn,0),n≥2为一个收缩,它表示f∈Aut(Cn),f(0)=0,且当n→∞时, fn(B)收敛于0,这里B是Cn中的闭球.若f∈Aut(Cn),f(0)=0,且具体形式为f:(z1,z2,…,zn)→(μ1z1,μ2z2,…,μnzn),其中μ1,μ2,…,μn都落在单位圆盘内,则称f为对角收缩.主Hopf流形的基本群G由一个收缩f生成.Verbitsky[8]研究了对角主Hopf流形上全纯向量丛.Mizuhara[9]根据f对三维的主Hopf流形进行了分类,本文讨论了其中一类线性非对角收缩的主Hopf流形上的线丛.

光滑流形M上的一个光滑复线丛E称作是平坦的,如果它允许一个平坦的结构,即在M上存在一个开覆盖,使得在此开覆盖上,E的过渡函数族都是C*=C-{0}中的常数[10].

Mall在文献[3]中证明了任意Hopf流形上的全纯线丛都是平坦的.

设L是X上的平坦的全纯线丛,因此L是W×C在其基本群表示作用下的商,其中W×C为X的万有覆盖空间上平凡线丛.设

ρL:π1(X)→C*

是X的基本群π1(X)的表示,则L是W×C在下面基本群π1(X)≅Z表示作用下的商:

这里ρL是π1(X)的一个表示

其中bm为b的m次幂.用Lb表示由π1(X)在上述作用下诱导的平坦向量丛,这里b∶=ρL(1).

本文考虑一类三维的主Hopf流形X,X由一个非对角收缩f生成,这里

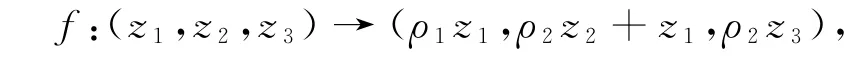
其中0<ρ1<ρ2<1.参见文献[9].

下面将给出

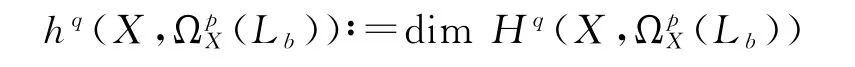
的计算公式以及有关计算结果.

取主Hopf流形X的一个开覆盖A={Ui}使得所有Ui为X的可缩的Stein子集,并且Ui∶=π-1(Ui)是W的开的Stein子集{U'ij}一个不交并,它们每一个同构于Ui:

因为平坦的全纯向量丛一定是具有平凡拉回的全纯向量丛,所以由文献[3],复形序列(1)是正合的.由上面正合的ˇcech复形序列(1),可以得到下面的上同调的长正合Douady序列:

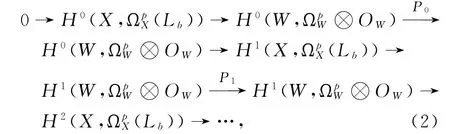
这里Pi∶=b-f*.由文献[11],知道H1(W,O)=0.因为

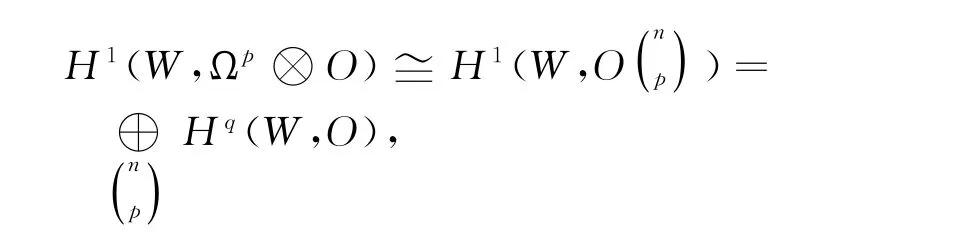
所以序列(2)可化为如下的长正合序列:

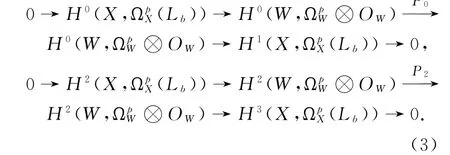
定义hp,qb∶=dim Hq(X,ΩpX(Lb)),由上面的正合序列(3),立即得到下面的结果:

由文献[12],对于b∈C*,那么P=bId-f*是一个Fredholm算子,其指标index P=dimker P-dimcoker P=0.因此有:

引理1 X是一个3维的主Hopf流形,Lb是X上的平坦的全纯向量丛,那么:

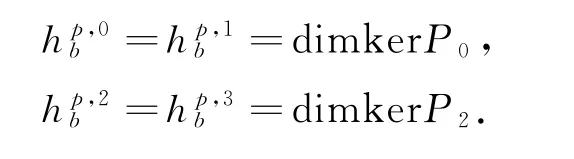
2　上同调维数的显式表达式

定理1 设X是一个3维的主Hopf曲面,X由一个非对角收缩f生成,这里

其中0<ρ1<ρ2<1.Lb∈H1(X,O*)是X上的一个平坦线丛,对于(m,n∈N),有如下结果(见表1).

证明 由引理1,我们只要计算dimker P0及dimker Pn-1.又由Serre对偶Hq(X,ΩpX(Lb))= Hn-q(X,Ωn-pX(Lb-1)),则可不必计算dimker Pn-1.

(i)计算h0(X,O(Lb)).

全纯截面ω∈Γ(W,O)可写为

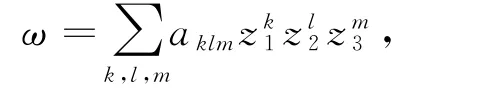
有:

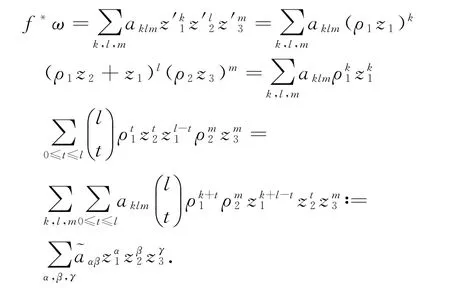
比较变量z1,z2,z3的指数,可以得到条件:

上面方程的解为:

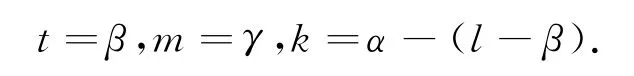
令j∶=l-β,则α=k-j,故j可取值:0,1,…,α.显然有l=β+j.

因此

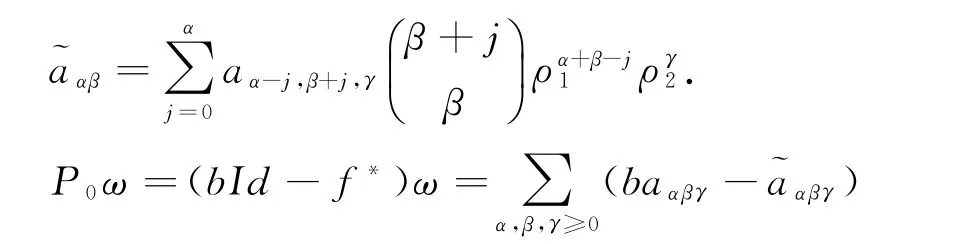
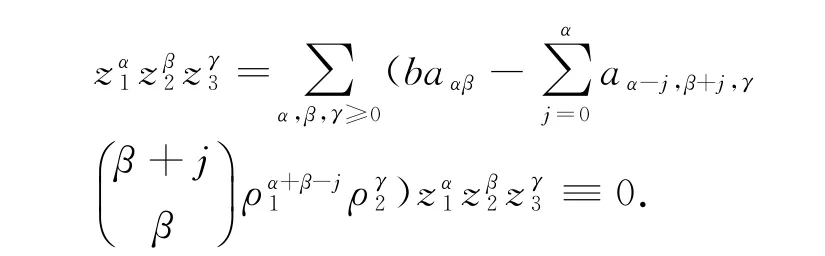
表1　上同调维数Tab.1 The dimension of cohomology

可以得到:

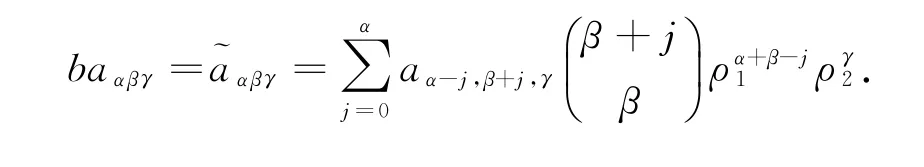
重新写成形式:

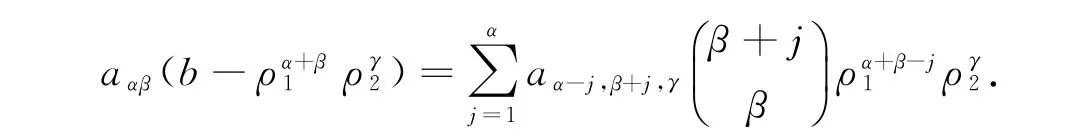
上面条件可重新写成齐次线性方程组:

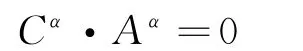
这里

以及

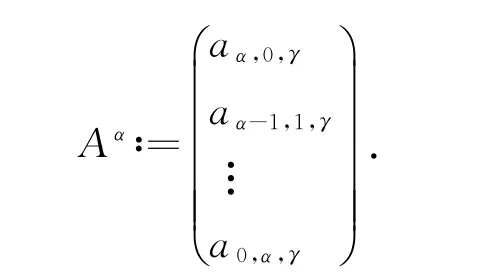
上面的齐次线性方程组有非零解Aα,当且仅当b -ρα1ργ2=0,此时aα,0,γ≠0,在此情形下解空间的维数为1.因此有

(ii)计算h0(X,Ω1X(Lb)).

全纯截面ω∈Γ(W,Ω1W)可写为

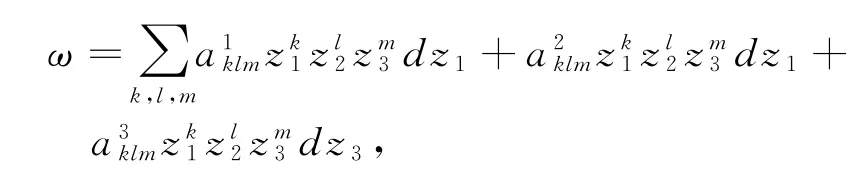
我们有:

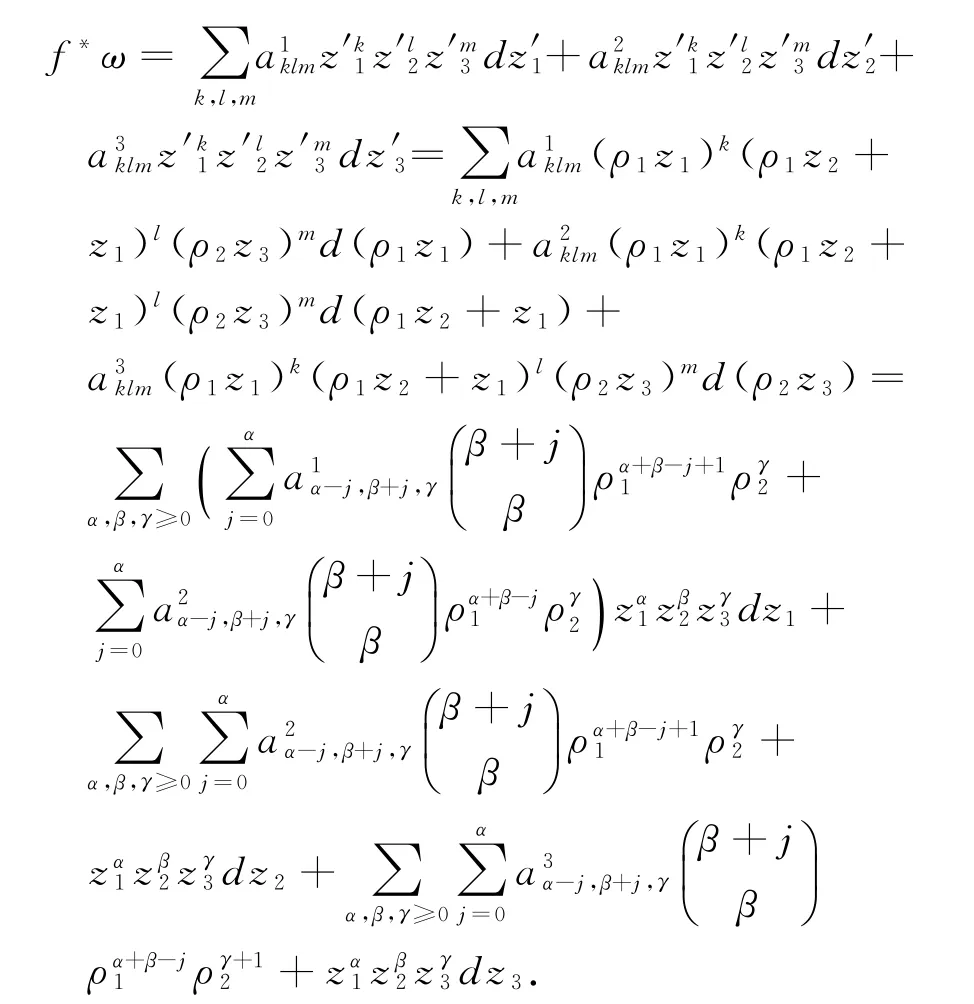
由P0ω=(bId-f*)ω=0得:

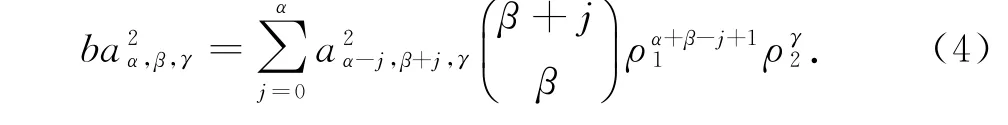
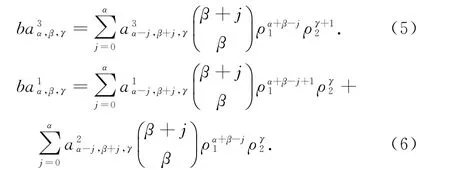
如(i)中的方法,式(4)有非零解当且仅当b=ρα+11 ργ2,此时a2α,0,γ≠0;式(5)有非零解当且仅当b=ρα1,此时a3α,0,γ≠0.因此式(6)可化简为:

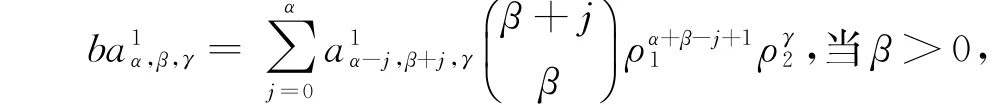
及

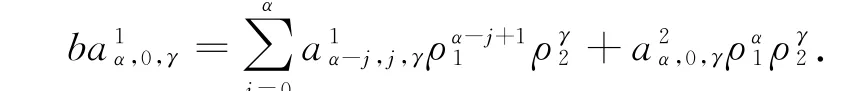
上面条件可重新写成线性方程组:

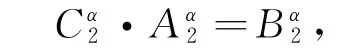
这里

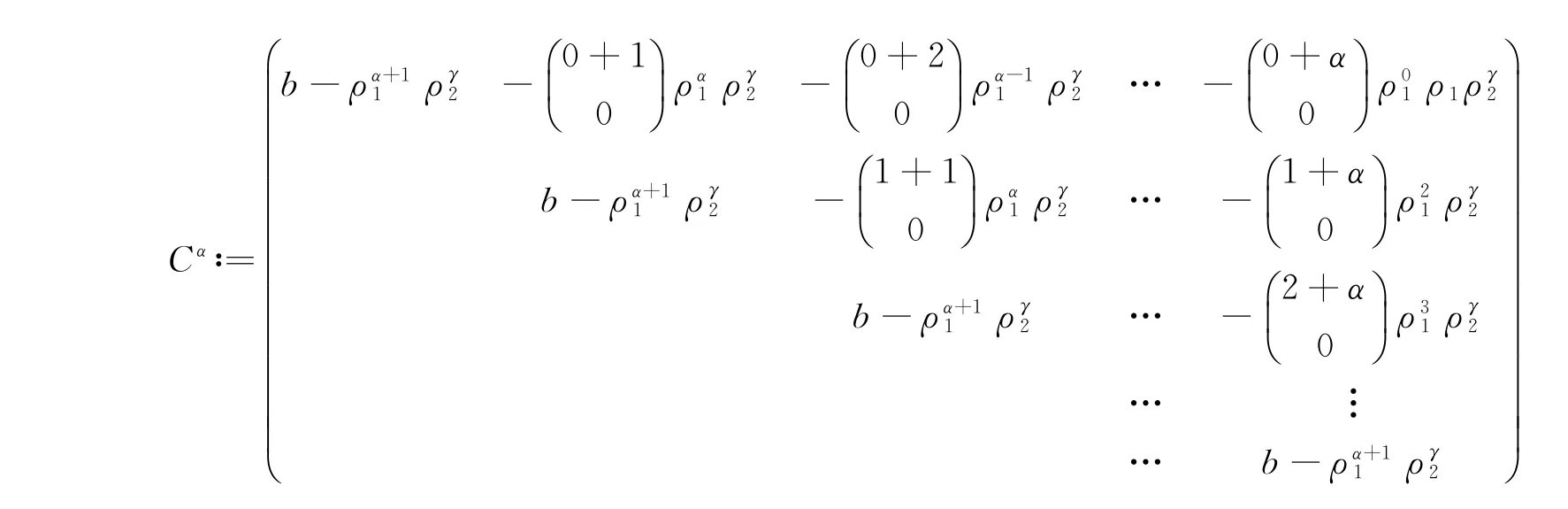
以及

若Bα2≠0,即a2α,0,γ≠0,则b=ρα+11 ργ2,那么此线性方程组的解空间维数为1.因此有:

(iii)计算h0(X,Ω2X(Lb)).

全纯截面ω∈Γ(W,Ω1W)可写为

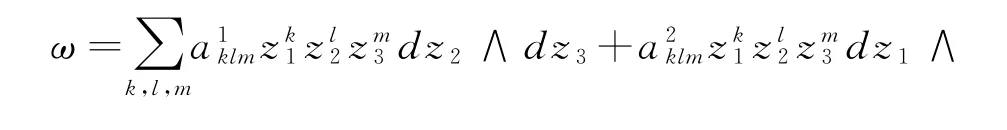
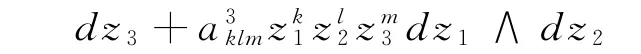
有

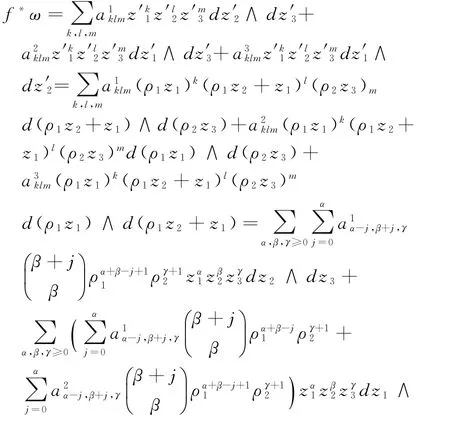
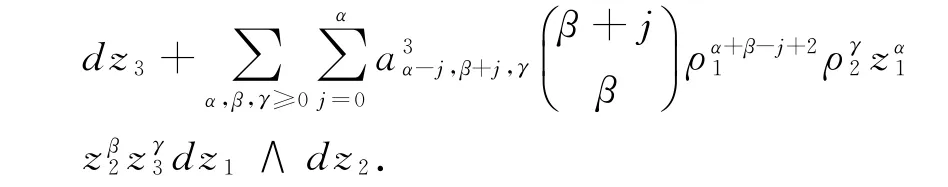
由P0ω=(bId-f*)ω=0得:

式(7)有非零解当且仅当b=ρα+11 ργ+12,此时a1α,0,γ≠0; 式(8)有非零解当且仅当b=ρα+21 ργ2,此时a3α,0,γ≠0.因此式(9)可化简为:

及

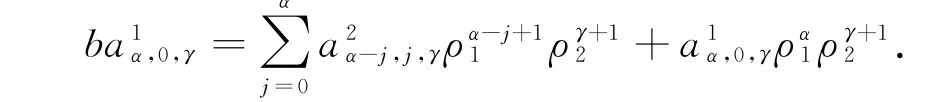
上面条件可重新写成线性方程组:

这里

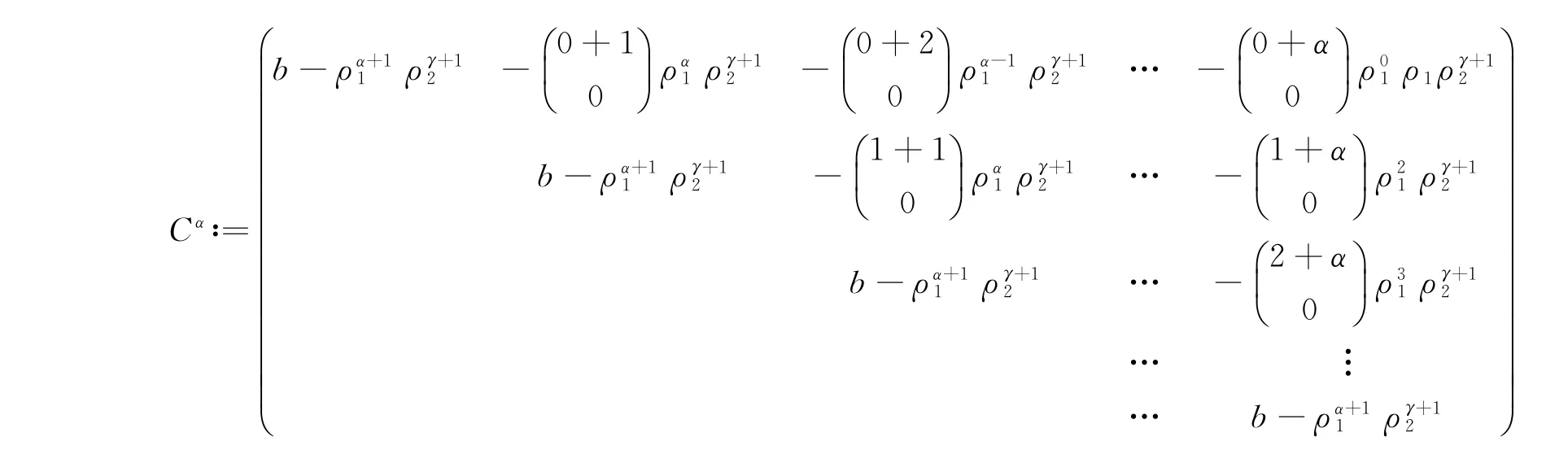
以及

若Bα3≠0,即a1α,0,γ≠0,则b=ρα+11 ργ+12,那么此线性方程组的解空间维数为1.因此有:

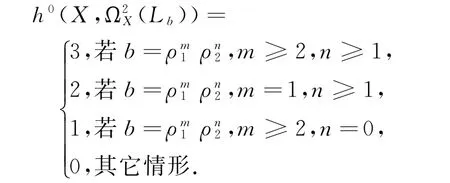
(iv)计算h0(X,Ω3X(Lb)).

全纯截面ω∈Γ(W,Ω3W)可写为

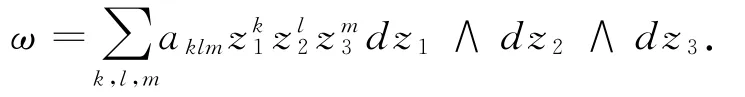
有:

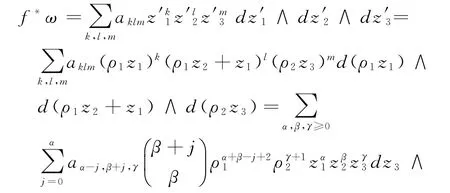
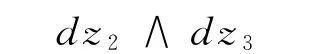
由P0ω=(bId-f*)ω=0得:

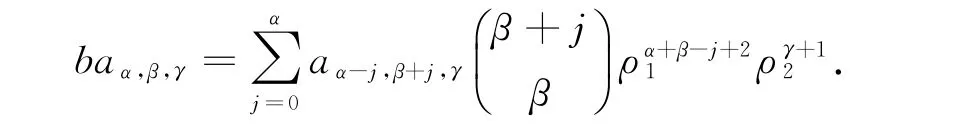
类似于(i)的计算得:

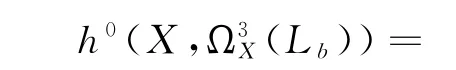
参考文献:

[1] BRIN ZANESCU V.Holomorphic vector bundles over compact complex surfaces[C]∥Lecture Notes in Mathematics 1624.Berlin:Springer-Verlag,1996:23-27.

[2] TELEMAN A,TOMA M.Holomorphic vector bundles on non-algebraic surfaces[J].Comptes Rendus Mathematique,2002,334(5):383-388.

[3] MALL D.The cohomology of line bundles on Hopf manifolds[J].Osaka J Math,1991,28:999-1015.

[4] GAN N,ZHOU X Y.Some results on holomorphic vector bundles over general hopf manifolds[J].数学进展,2005, 34(4):245-248.

[5] GAN N,ZHOU X Y.The cohomology of line bundles on non-primary Hopf manifolds[J].Acta Mathematica Sinica,English Series Feb,2007,23(2):289-296.

[6] GOLDBERG S I.Curvature and homology[M].New York:Academic Press,2011:132-145.

[7] BARTH W,PETER C.Compact complex surfaces[M]. Berlin:Springer-Verlag,2003:225-227.

[8] VERBITSKY M.Holomorphic bundles on diagonal Hopf manifolds[J].Izv Ross Akad Nauk Ser Mat,2006,70: 867-882.

[9] MIZUHARA A.Three dimensional Hopf manifolds[J]. Acta Human Sci Univ Sangio Kyotien Natur Sci Ser, 1978,8:5-21.

[10] KOBAYASHI S.Differential geometry of complex vector bundles[M].New Jersey:Iwanami Shoten and Princeten University Press,1987:4-7.

[11] HAEFLIGER A.Deformation of transversely holomorphic flows on spheres and deformation of Hopf Manifolds[J]. Composition Math,1985,55:241-251.

[12] MALL D.Contractions,Fredholm operators and the cohomology of vector bundles on Hopf manifolds[J].Arch Math,1996,66:71-76.

The Hodge Numbers of Line Bundles on Three Dimensional Primary Hopf Manifolds

GAN Ning
(School of Sciences,Jimei University,Xiamen 361021,China)

Abstract:Let X be a three dimensional primary Hopf manifold C3-{0}/,where g is a non-diagonal contraction.We computed the Hodge numbers of the cohomology group of holomorphic line bundles over X,by the method of Douady sequence and group action.These results will facilitate the study of the structure of line bundles of non-algebraic manifolds.

Key words:Hopf surface;cohomology;holomorphic line bundles;Hodge numbers

基金项目:国家自然科学基金(10826093);福建省自然科学基金(2010J05010)

收稿日期:2015-05-29 录用日期:2015-08-23

doi:10.6043/j.issn.0438-0479.2016.02.014

中图分类号:O 174.56

文献标志码:A

文章编号:0438-0479(2016)02-0227-06

Email:ganning@jmu.edu.cn

引文格式:甘宁.一类三维Hopf流形上全纯线丛的Hodge数[J].厦门大学学报(自然科学版),2016,55(2):227-232.

Citation:GAN N.The Hodge numbers of line bundles on three dimensional primary Hopf manifolds[J].Journal of Xiamen University(Natural Science),2016,55(2):227-232.(in Chinese)