N-S方程强黏性接触间断波的渐近稳定性
2016-04-11郑婷婷
郑婷婷
(福建农林大学计算机与信息学院,福建福州350002)
N-S方程强黏性接触间断波的渐近稳定性
郑婷婷
(福建农林大学计算机与信息学院,福建福州350002)
摘要:构造了一类具有一般性质的强黏性接触间断波,它的初始一阶导数的L2模以及温度振幅|θ+-θ-|为一般常数.并且该黏性接触间断波就是N-S方程自由边界问题渐近稳定极限,这种强黏性接触间断波比以往的黏性接触间断波更具有一般性意义.本文的证明方法是利用抛物方程的时间空间衰减估计进行N-S方程的常规能量估计.
关键词:自由边界;强黏性接触间断;渐近稳定
本文考虑的是一维N-S方程流体力学模型
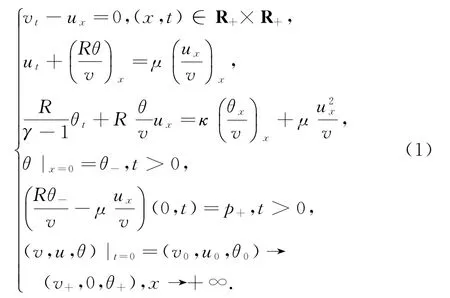
此处v+与θ±(θ+>θ-)为正常数,而v0,θ0>0.并且v=v(x,t),u=u(x,t),θ=θ(x,t)与Rθ/v= p(v,θ)为对应的体积、速度、温度和压力.
这个问题被称为自由边界问题[1].该问题渐近稳定性的研究较多,尤其是各种弱波(即|θ--θ+|充分小)的小扰动问题,对N-S方程自由边界问题、Cauchy问题以及流入问题都作了深入讨论[2-9].然而,对于各种强波(即|θ--θ+|非充分小)的稳定性讨论却进展艰难,主要原因是|θ--θ+|的充分小条件在以往的参考文献证明中都是必不可少的重要条件.文献[10]将初值限制改为‖θ0-θ+‖L1≫1.
本文去掉了文献[10]中温度初值的限制条件‖θ0-θ+‖L1(R+)≫1,证明了|θ+-θ-|为任何常数,而温度初值满足‖θ0-θ+‖L1(R+) 设Hl(R+)表示第l阶Sobolev空间,并且 C或Ci(i=1,2,3…)表示一般正常数,C(z)表示关于z的常数且limz→0C(z)=0.ε与εi(i=1,2, 3,…)为满足Cauchy-Schwarz不等式的常数. 借用文献[2,5,10]构造的想法,考虑方程组 其中: 且常数α=κ-1/2(见引理1),常数δ0>0充分小.则存在与α,δ0无关的常数M0,使得Θ0满足如下关系: 实际上,这些估计式可以通过简单的微积分运算,并且结合基本的因式分解法an-bn=(a-b)∑n-1i=0an-1-ibi获得,其中a,b>0. 由方程组(2)可知 参考文献由[10]可知上述Θ满足如下关系: 结合式(2)中(V,U,Θ)的关系以及式(6)~(12)可得,当式(5)中的κ→0,在任意有限时间区间内(V, U,Θ)为黏性接触间断波,即: 引理1 设α=κ-1/2,p≥1且t∈[0,T],则 ‖(V-V,UU,Θ-Θ)‖Lp(R+)→0,κ→0. 证明 该引理主要利用了抛物方程(5)的时间衰减估计与热核系数κ之间的关系得证,证明过程见文献[10]. 设(v,u,θ)满足式(1),(V,U,Θ)满足式(2)且 φ(x,t)=v(x,t)-V(x,t), ψ(x,t)=u(x,t)-U(x,t), ζ(x,t)=θ(x,t)-Θ(x,t).(13) 将式(13)代入式(1)可得 结合式(2)可得式(14)中的初边值条件满足兼容性条件,且 不妨设 则对于区间I∈[0,∞),定义 那么本文主要结论如下: 定理1 设常数C>1与η0充分小,若θ0(x)-θ+∈L1(R+),‖(v0-V0,u0-U0,θ0-Θ0)‖L2(R+)≤η0,‖(v0x-V0x,u0x-U0x,θ0x-Θ0x)‖L2(R+)≤C,则式(14)存在唯一解(φ,ψ,ζ)∈X([0,∞))且 定理1的证明必须结合先验估计和局部解的存在性完成,局部解的存在性证明可以见文献[2].此处主要对如下的先验估计进行证明 命题1 (先验估计)设(φ,ψ,ζ)∈X([0,t])为式(14)的解,存在与t和(v,θ)无关的正常数C(δ0)<1与C>1,使得若m≤v,θ≤M且1 首先处理相关的边界条件.设φ(t)=φ(0,t),因为Ux(0,t)=Vt(0,t)=0,则由式(14)边值条件可得 通过对微分方程(18)的计算, 命题以及定理的证明需要通过下面一系列引理来完成. 引理2 若C(δ0)>0为关于δ0的小常数,则 证明 同理得 则 由式(6)与式(12)可得 该引理得证. 引理3 设ε1>0与C(δ0)>0为充分小常数,则 证明 设Φ(z)=z-ln z-1,Ψ(z)=z-1+ln z-1,类似文献[2],将式(14)的第2和3个方程分别乘以ψ与,并且相加,再结合第1个方程可得 将式(18)在(0,t)×R+上积分,并结合式(6)~(12), Cauchy-Schwarz不等式以及引理2,则该引理得证. 引理4 设ε2>0,C(δ0)>0为充分小常数,则 证明 首先由于ψx=φt, 且ψ(0,t)=C(lnΘ)x(0,t). 将式(14)第2式乘以ψxx并且在(0,t)×R+上积分,类似文献[10],结合引理2,引理3以及式(6)~ (13),(17),(19)可得 将式(14)第3式乘以ζxx并且在(0,t)×R+上积分,类似文献[10],结合引理2,引理3以及式(6)~ (13),(17),(20)可得 结合式(20)和(21),则该引理得证. 引理5 设ε3>0和C(δ0)>0为充分小常数,则 并且 因为 结合ψ(0,t)在式(14)中的定义以及φt(0,t)在式(19中的定义,则 将式(25)两边在(0,t)×R+上积分并结合Cauchy-Schwarz不等式,上述估计式(24)与边界条件(26)以及引理2~4可得 于是该引理得证. 结合引理2~5,当δ0与‖(φ0,ψ0,ζ0)‖充分小,则存在充分小的常数δ,使得 且 则C5≤|v|≤C6且C7≤|θ|≤C8,此处C5,C6,C7和 C8为与v和θ无关的常数,则命题1得证.并且 则 即定理1可以得证. [1] MATSUMURA A.Inflow and outflow problems in the half space for a one-dimensional isentropic model system of compressible viscous gas[J].Meth Appl Anal,2001,8 (4):645-666. [2] HUANG F M,MATSUMURA A,SHI X.On the stability of contact discontinuity for compressible Navier-Stokes equations with free boundary[J].Osaka J Math, 2004,41(1):193-210. [3] HUANG F M,MATSUMURA A,XIN Z P.Stability of contact discontinuity for the 1-D compressible Navier-Stokes equations[J].Arch Ratonal Mech Anal,2005, 179:55-77. [4] HUANG F M,XIN Z P,YANG T.Contact discontinuity with general perturbations for gas motions[J].Adv Math,2008,219:1246-1297. [5] HUANG F M,Zhao H J.On the global stability of contact discontinuity for compressible Navier-Stokes e-quations[J].Rend Sem Mat Univ Padova,2003,109: 283-305. [6] HUANG F M,LI J,MATSUMURA A.Asymptotic stability of combination of viscous contact wave with rarefaction waves for one-dimensional compressible Navier-Stokes system [J].Arch Rat Mech Anal,2010,197: 89-116. [7] MA S X.Zero dissipation limit to strong contact discontinuity for the 1-D compressible Navier-Stokes equations [J].JDE,2010,248:95-110. [8] HAKHO H.Global stabillity of viscous contact wave for 1-D compressible Navier-Stokes equations[J].JDE,2012, 252:3482-3505. [9] LIU T P,XIN Z P.Pointwise decay to contact discontinuities for systems of viscous conservation laws[J].Asian J Math,1997,1(1):34-84. [10] ZHENG T.Stability of a strong viscous contact discontinuity in a free boundary problem for compressible Navier-Stokes equations[J].Nonlinear Analysis:Real World Applications,2015,25:238-257. Stability of a Strong Viscous Contact Discontinuity for Navier-Stokes Equations ZHENG Tingting Abstract:In this paper,we construct a general strong viscous contact discontinuity as the norm of the first derivative of the initial data and its strength can be ordinary constants.We also prove that this kind of viscous contact discontinuity is just the asymptotic stability limit of a free boundary problem for Navier-Stokes equations.This type of strong viscous contact discontinuity is more significant than the weak wave researched before.Here we primarily use the time and space estimates of a parabolic equation to obtain the elementary energy estimate for Navier-Stokes equations. Key words:free boundary problem;strong viscous contact discontinuity;asymptotic stability 基金项目:国家自然科学基金数学天元基金(11426062);福建省教育厅科技计划项目(JA12104) 收稿日期:2015-06-02 录用日期:2015-08-02 doi:10.6043/j.issn.0438-0479.2016.02.012 中图分类号:O 175.27;O 241.83 文献标志码:A 文章编号:0438-0479(2016)02-0216-05 Email:nljj2011@126.com 引文格式:郑婷婷.N-S方程强黏性接触间断波的渐近稳定性[J].厦门大学学报(自然科学版),2016,55(2):216-220. Citation:ZHENG T T.Stability of a strong viscous contact discontinuity for Navier-Stokes[J].Journal of Xiamen University (Natural Science),2016,55(2):216-220.(in Chinese)
1 黏性接触间断波的构造
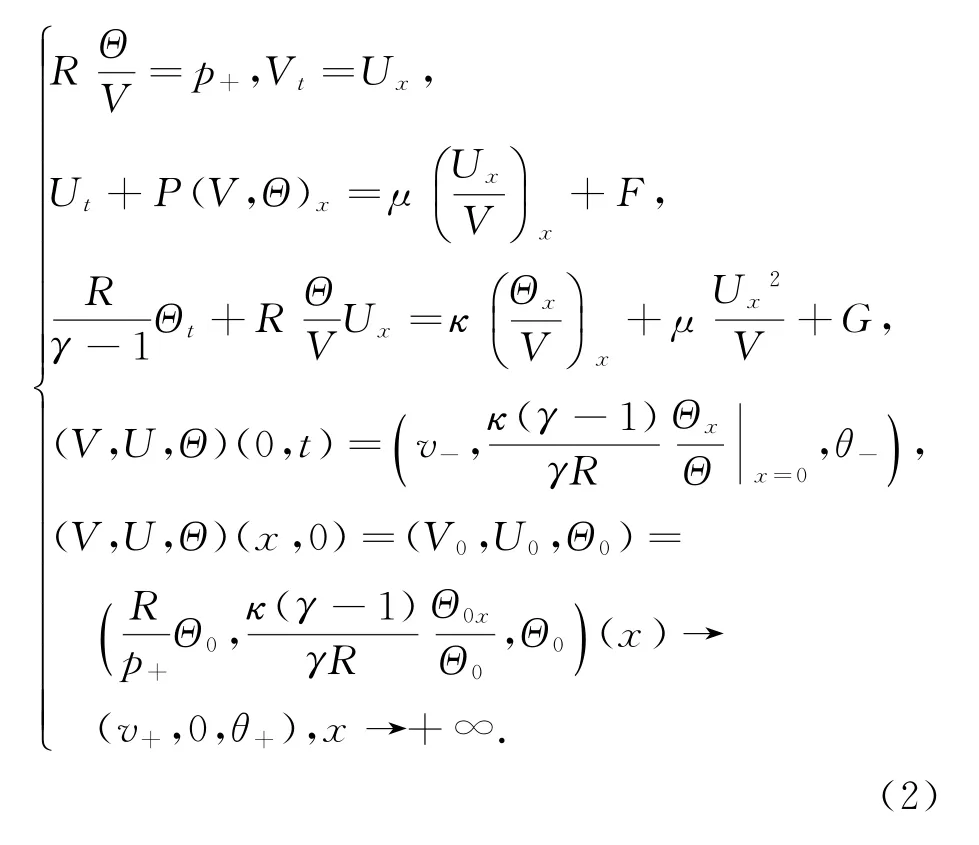
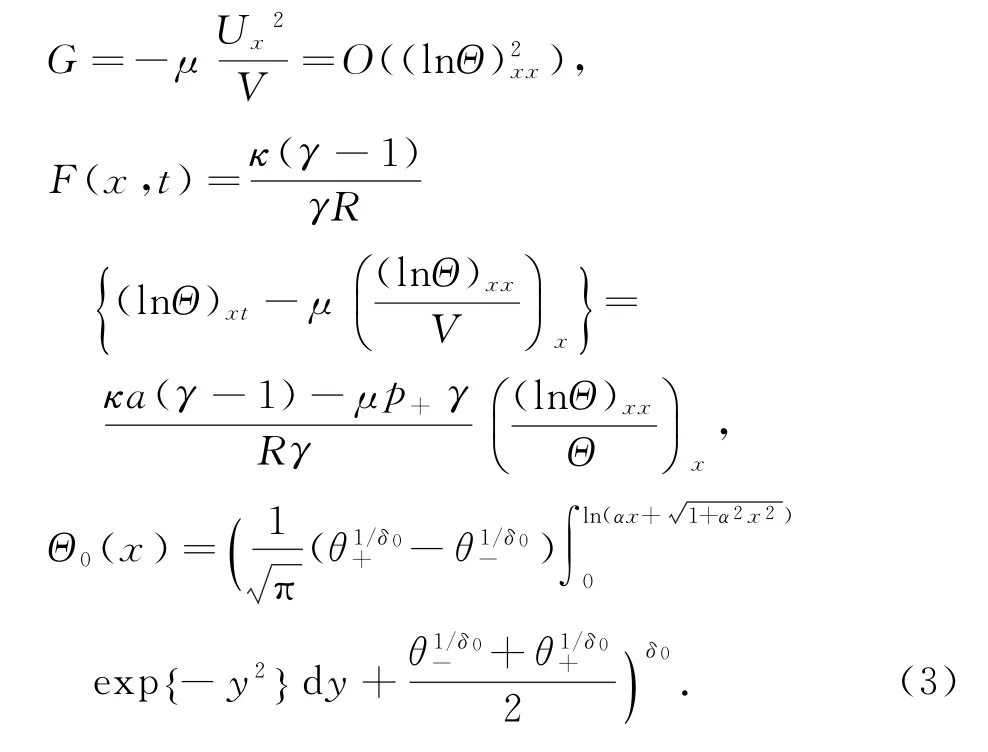
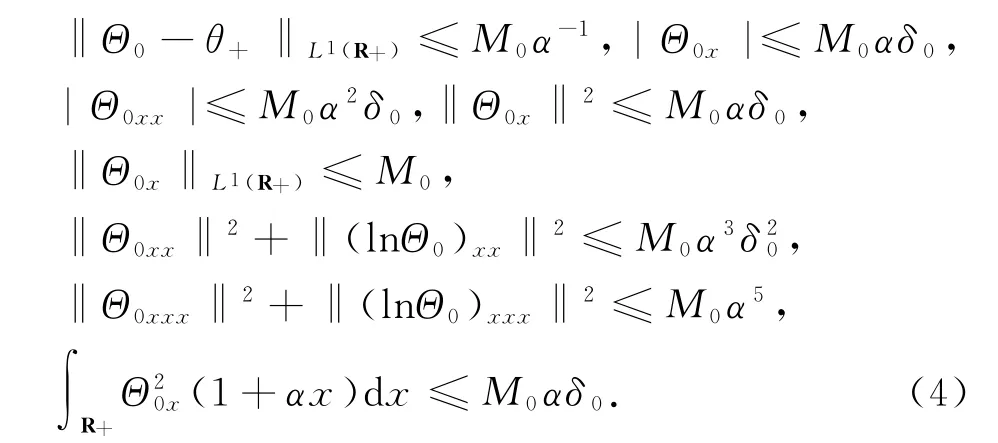

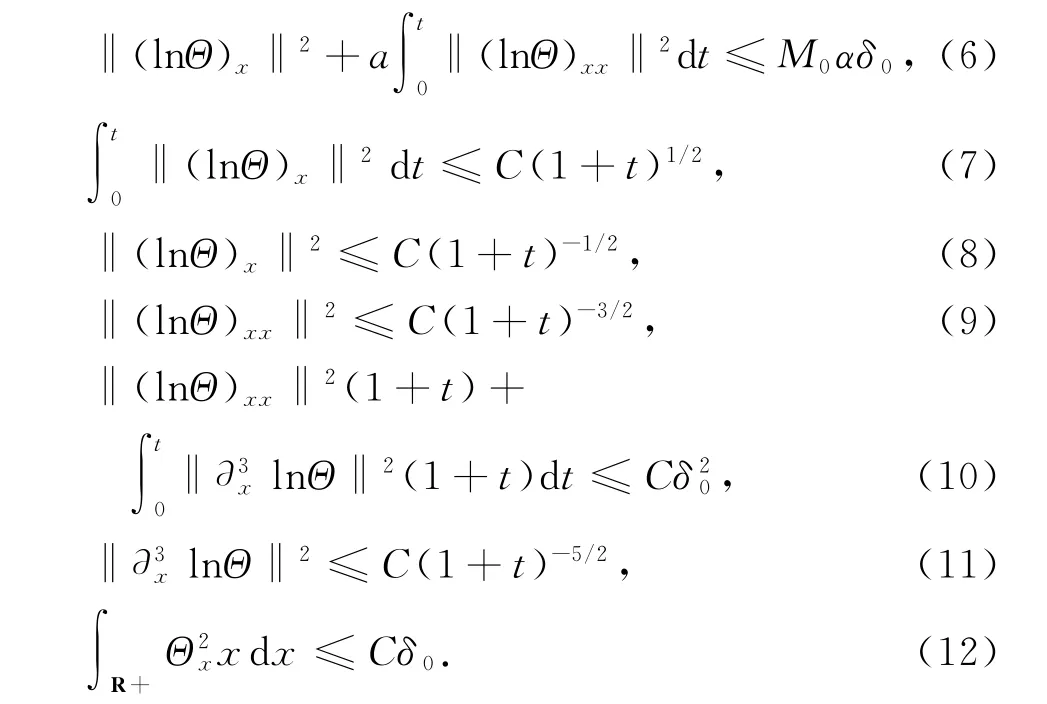
2 主要结论
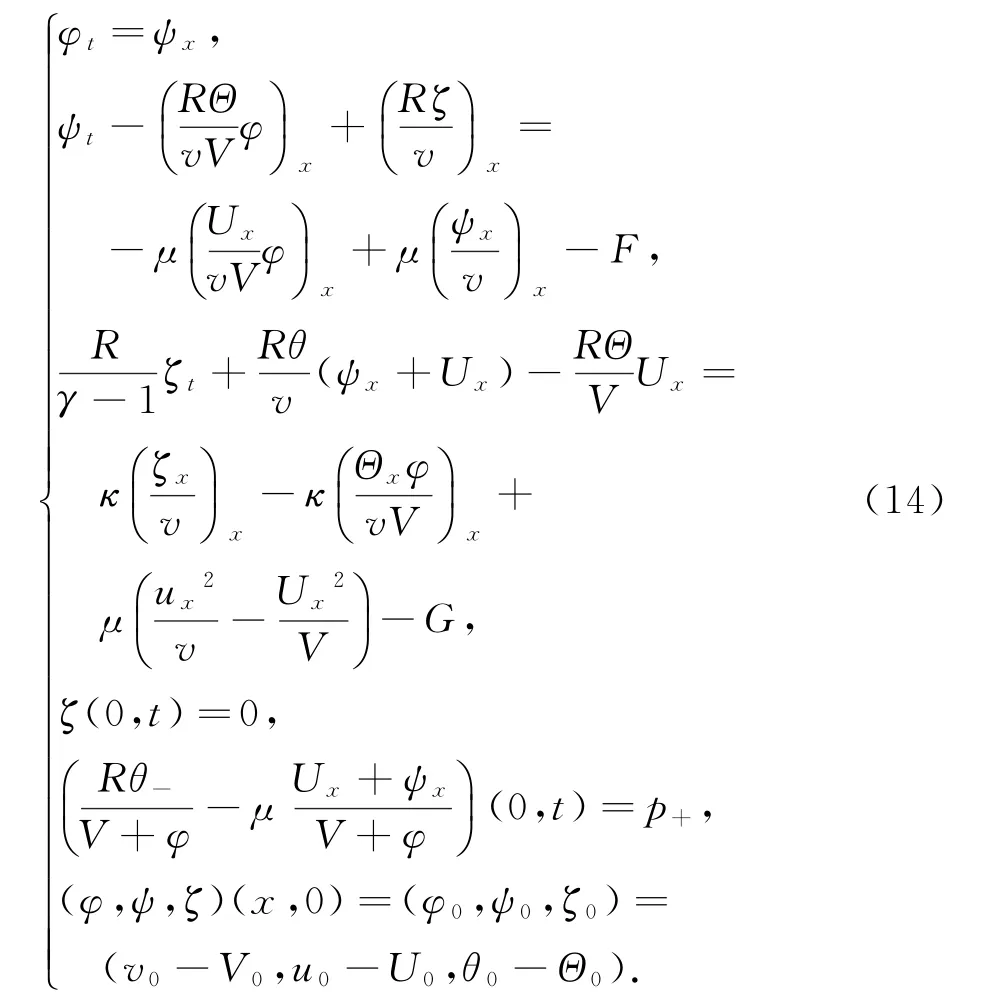

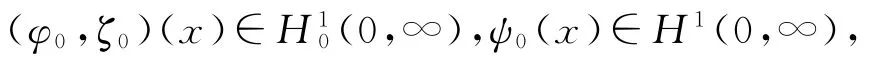
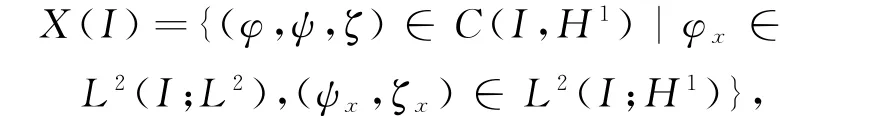
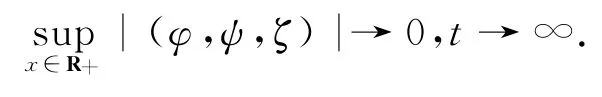
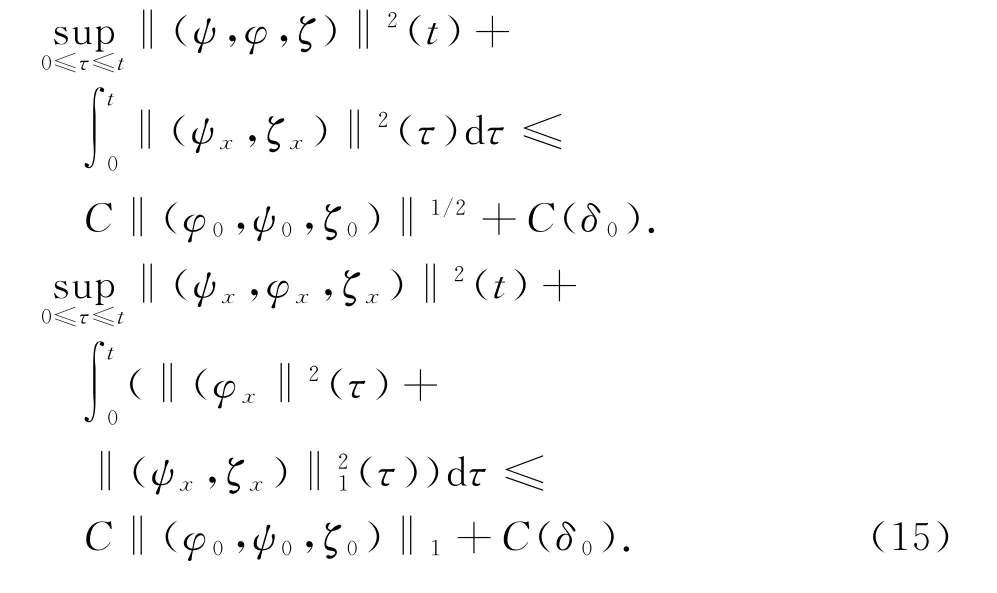
3 定理的证明

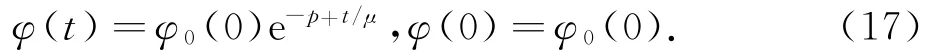
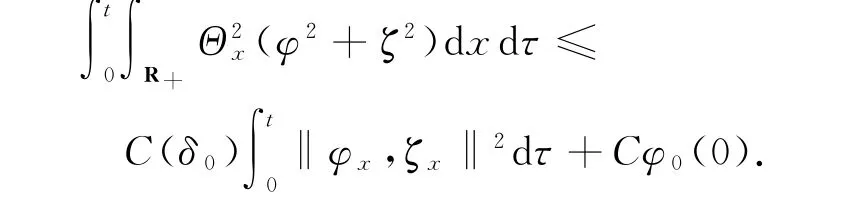

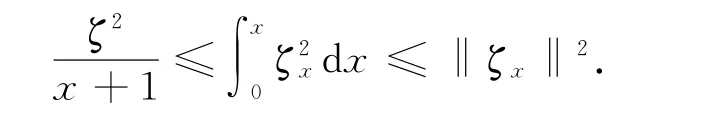

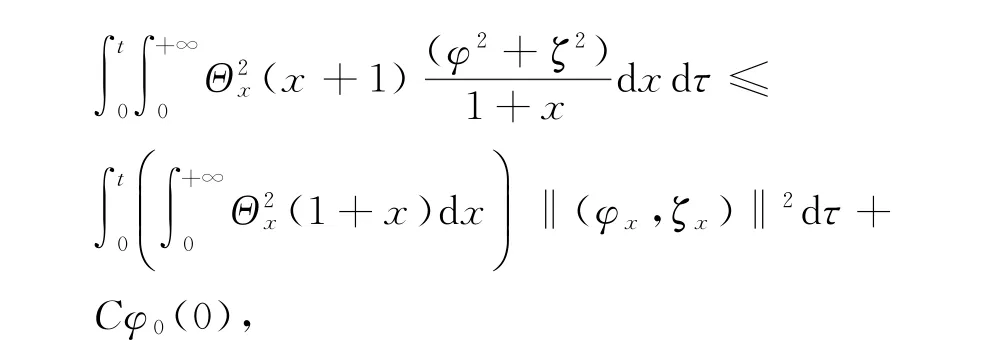
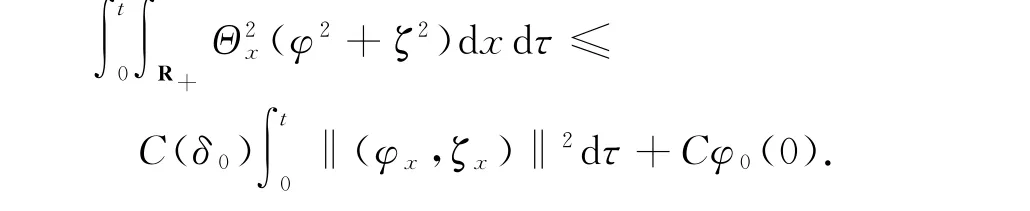

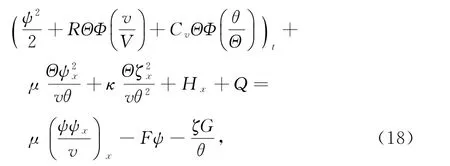
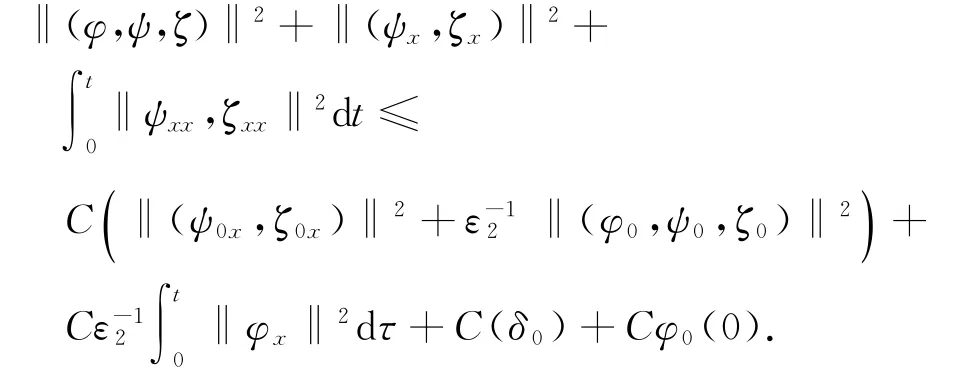
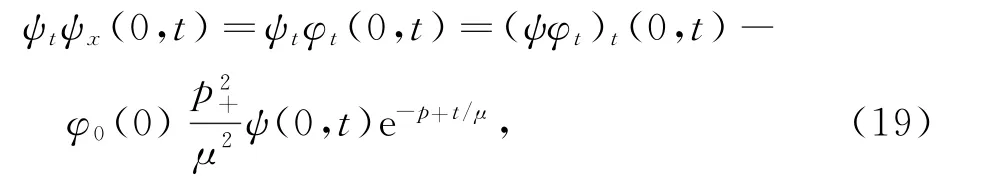
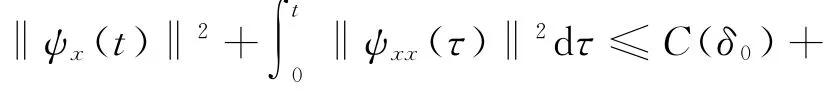
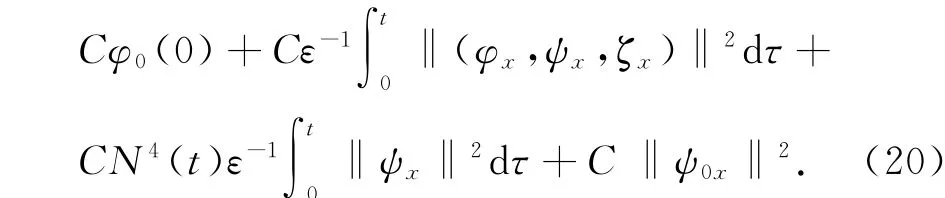
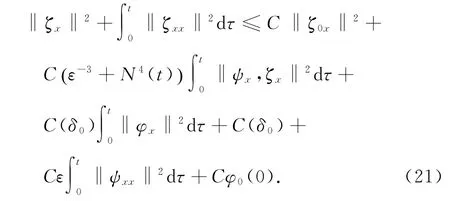
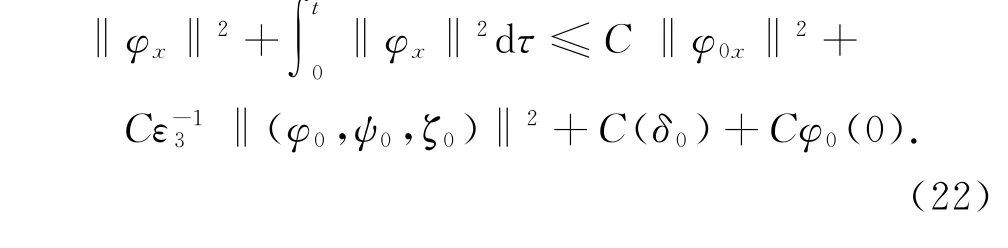
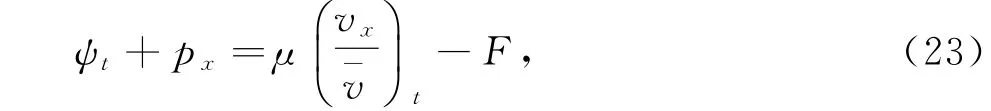
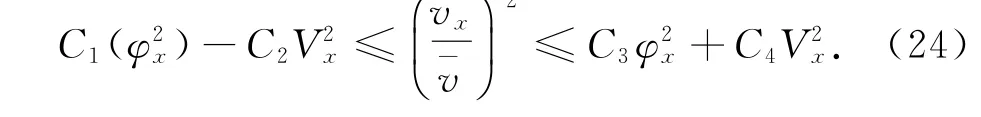
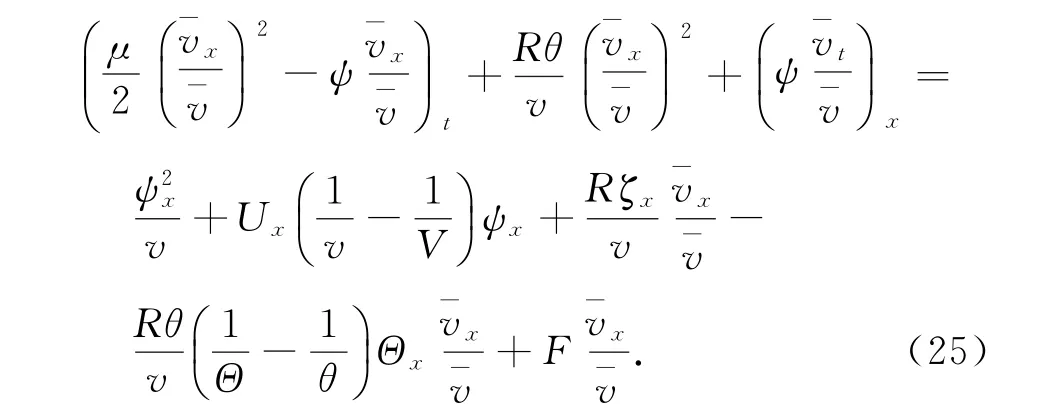

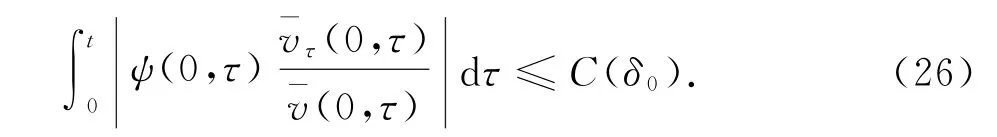
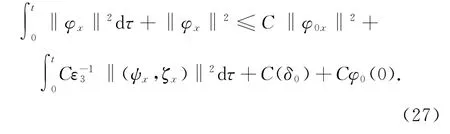
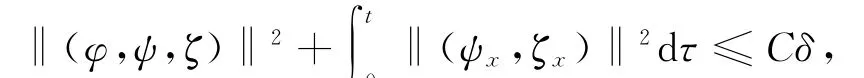

(Computer and Message Science College,Fujian Agriculture and Forestry University,Fuzhou 350002,China)
