无线传感器网络节点定位中移动信标的路径规划

张　强，张　庆，张　磊，于纪言，贾方秀

(1.南京理工大学 智能弹药技术国防重点科学实验室，南京　210094；

2.豫西工业集团有限公司 军品研发中心，河南 南阳　473000)



无线传感器网络节点定位中移动信标的路径规划

张强1，张庆1，张磊2，于纪言1，贾方秀1

(1.南京理工大学 智能弹药技术国防重点科学实验室，南京210094；

2.豫西工业集团有限公司 军品研发中心，河南 南阳473000)

摘要：分别研究了2种不同确定路径下(SCAN轨迹和HILBERT轨迹)的节点定位性能。通过Enthought Canopy软件仿真试验得到结果表明：和信标的随机移动相比，任何覆盖整个区域的确定的信标移动路径具有明显的优势；当移动信标以小于通讯范围的分辨率遍历节点网络区域时，SCAN路径具有更低的定位误差；当轨迹的分辨率大于通讯范围时，HILBERT轨迹提供的精度明显更高。

关键词：无线传感器网络；移动信标；节点定位；路径规划

Citation format:ZHANG Qiang, ZHANG Qing,ZHANG Lei, et al.Path Planning of Mobile Beacon in Wireless Sensor Network Node Localization[J].Journal of Ordnance Equipment Engineering,2016(2):144-149.

随着传感器技术、通信技术和计算机技术的发展，无线传感器网络技术被广泛运用于军事、医疗、环境监测、农业、工业和智能家居等领域[1]。在无线传感器网络的应用中，各个传感器节点采集到的数据必须结合其位置信息才有意义[2]。例如，智能雷和组网雷阵在打击坦克和超低空飞行目标以及封锁敌方机场时，雷弹自身的位置信息是其目标定位、跟踪和协同打击的基础。另外，位置信息还可辅助进行无线传感器网络的路由、拓扑管理，确定路径规划和数据传输方案等。因此，节点定位成为无线传感器网络的关键技术之一[3]。

(现有的大多数使用信标节点或者无需信标节点的无线传感器网络节点定位方法，结果都不够精确。这是因为静止的信标并不能覆盖整个网络，未被覆盖的节点只能近似估计自己的位置。通常，信标节点越多，定位精度也越高[4]。然而，由于传感器网络中节点体积、能量、成本等方面的限制，信标数量的增加将会增加整个网络成本。移动信标的引入，正好解决了这些问题。为了在信标移动速度给定的条件下最大限度地提高定位精度，移动信标的路径规划是一个基础问题。

在文献[5]中，移动信标遍历被监测的区域，通过来自未知传感器节点信号的接收信号强度指标定位所有的节点，并采用鲁棒扩展卡尔曼滤波器(REKF)作为位置估计器。在文献[6]中，节点基于来自机器人的信号和它们相邻节点的连通性来定位自身位置。文献[7]提出了移动辅助定位(MAL)算法，该算法需要几个确定的节点之间的距离和RSSI的对应关系来修正未知节点的估计位置。以上方法中移动信标都是随机移动的。

文献[8]讨论了寻找一个良好的移动信标运动轨迹的问题，作者提出了两个重要的观点。第一，当移动信标接近节点时节点最容易定位，因为在此状态下节点接收到的信号强度(RSS)最大。第二，共线信号(由信标在同一条线段上移动时发出几个信号)是不能准确定位的，因为传感器无法判断它在移动信标的哪一边，因此必须要至少有3个不共线的信号，但是没有提出具体的路径解决方案。

本文研究了信标确定的移动轨迹，以期最大限度地提高传感器网络的定位精度。相对于信标的随机运动，确定的运动轨迹可以大大降低平均定位误差。本文详细研究了两种不同的确定轨道：SCAN和HILBERT。研究结果显示，在这两个轨迹中，当轨迹具备良好的分辨率时，SCAN轨迹的定位性能更好。当分辨率较大时，HILBERT轨迹的定位性能更好。

1定位算法和信标轨迹

1.1定位算法

在研究不同信标移动轨迹定位精度时，本文参考了Sichitiu等人在文献[8]中提出的算法，该算法用接收信号强度指标(RSSI)来测量距离，用贝叶斯推论来估算未知节点的位置。在运行算法之前，需要构造距离的概率分布函数(PDF)表，此表存储在每一个节点上，并且将RSSI值映射到PDF上。当移动信标遍历传感器节点部署区域时，它就周期性地广播信号数据包，这些数据包包含移动信标通过GPS单元获得的自身坐标(xb,yb)。当节点接收到一个信号数据包时，它就在PDF表中执行一次查找，获取数据包中RSSI对应距离的概率分布函数。传感器节点在其位置估计中利用以下约束优化其位置精度：

Constraint(x,y)=PDFRSSI(d((x,y),(xb,yb)))∀(x,y)∈

(1)

式(1)中：PDFRSSI为概率分布函数；d((x,y),(xb,yb))是坐标点(x,y)和(xb,yb)之间的欧氏距离；xmin，xmax，ymin和ymax是传感器部署区域的边界坐标。

存储在PDF表中的RSSI的最大值对应最小的距离，对其运用循环约束

(2)

式(2)中dmin是RSSI最大值对应的距离。基于先前的位置估计OldPosEst和约束条件用贝叶斯推论计算各个节点新的位置估计值NewPosEst：

(3)

节点每接收一次信号包便重复此过程，直到移动信标远离，或者节点接收达到了信号的最大数量值。该节点用最后的位置估计值PosEst去计算其最佳位置坐标(x′,y′)，方法如下：

(4)

1.2信标的移动轨迹

传感器网络定位所需移动信标的最优轨迹，从本质上讲有两个功能[10]：① 提供网络覆盖。移动信标提供良好的覆盖范围可以确保其遍历节点区域中的所有节点。② 提供优质的信号。对于位置未知的节点，若一组(至少3个)信号是非线性的，而且它们的信号强度可以映射到距离上，则对于传感器来说这组信号就是“优质的”。本研究选择SCAN和 HILBERT两个确定轨迹，通过仿真分析两条轨迹在不同分辨率下的定位性能。

SCAN是简单、容易实现的轨迹。移动信标沿着一个维度遍历网络区域，如图1(a)示。在此图中，移动信标沿着y轴移动，平行于y轴的两条连续的轨迹之间的距离定义为轨迹分辨率Q。如果传感器的通信范围为R，则分辨率最大为2R，以确保所有传感器都能接受到信号。

HILBERT曲线在高维度空间里创建点的线性排序，这可以保留点的物理邻接性。用基于位操作、有限状态图和递归结构的算法生成HILBERT曲线[9]，一个n阶的HILBERT曲线将2维空间划分为4n个方形区域，并且用4n条线段连接这些区域的中心，每条线段的长度等于方形区域的边长。HILBERT轨迹的分辨率Q定义为每条线段的长度，如图1(b)示。

2仿真实验及分析

2.1构建PDF表

在进行仿真试验之前需要构建算法需要的PDF表。本文参考文献[8]的方法，使用高斯函数来拟合RSSI测量信号强度分布概率密度函数。使用基于CC2500模块的无线收发器，在操场上每隔2 m测量RSSI，每个位置测量600次，并计算每个信号强度值的平均距离和标准偏差，结果如图2。把这些信息存储在PDF表中，并且存于网络中的每个节点上，未知节点接收到的信号强度通过节点中内嵌的概率分布函数计算本节点与信号来源节点之间的距离。如图2(c)，是此函数在RSSI=-40 dBm时的一个概率分布。但在实际测量和计算中发现，当RSSI值等于-118 dBm时对应的物理距离是52 m，超过这个距离后，由于反射、散射和多径传播的影响，信号强度值与距离对应关系的概率分布函数不再近似于高斯分布，因此在本文的PDF表中只包含RSS大于-118 dBm 的值。

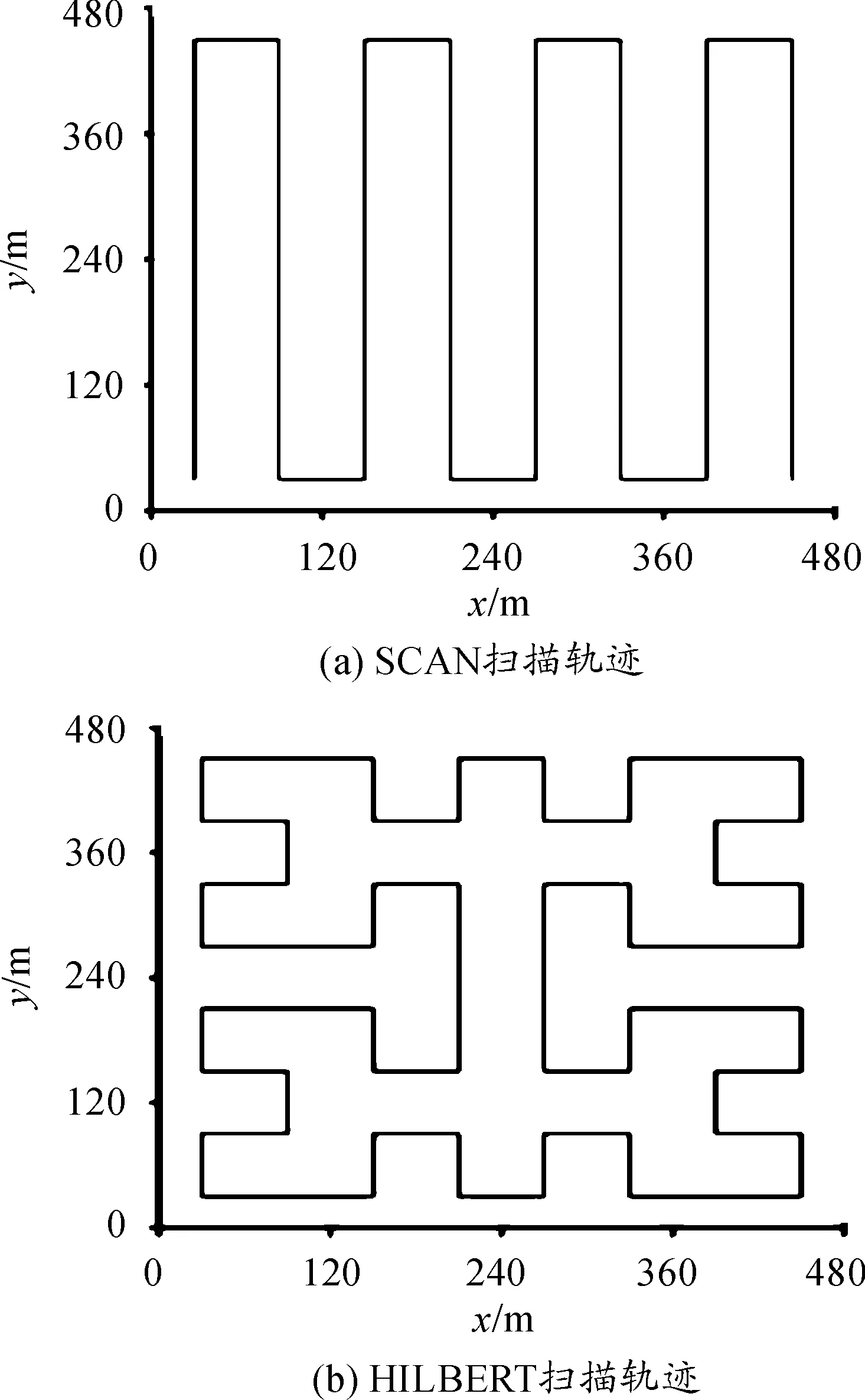
图1　扫描轨迹

2.2仿真设置

本文使用Enthought Canopy编辑器进行仿真试验。Enthought Canopy编辑器是一个全面的python语言分析环境，具有强大的迭代数据分析、数据可视化和应用程序开发等功能。

在仿真实验中分析每个轨迹在3个不同的分辨率：30 m，50 m和 75 m的定位性能。传感器节点部署区域的尺寸在每个仿真中都等于16×Q，Q是分辨率。如此设定的区域大小分别为：480 m×480 m，800 m×800 m和1 200 m×1 200 m。由于节点的平均定位误差并不依赖于节点的密度，而是仅仅取决于信标移动轨迹的分辨率，分辨率决定了节点接收到信号的数量和品质，因此在3个区域中采用相同的节点密度，传感器节点数分别为72、200和392个。因为实际中传感器的布撒是随机的，传感器散布的拓扑结构是未知的，因此用随机分布模拟传感器的散布状态，并设定信标的移动速度为2 m/s，节点通讯范围50 m，在此条件下评估所选择轨迹的性能。

图2　信号强度与距离的关系

图3(a)是分辨率为75 m的SCAN轨迹中，在阴影区域内的节点只能接收到线性信号；图3(b)为HILBERT轨迹的分辨率大于0.71倍通讯范围时，图中阴影区域内的节点与移动信标间的最短距离将大于通讯范围。

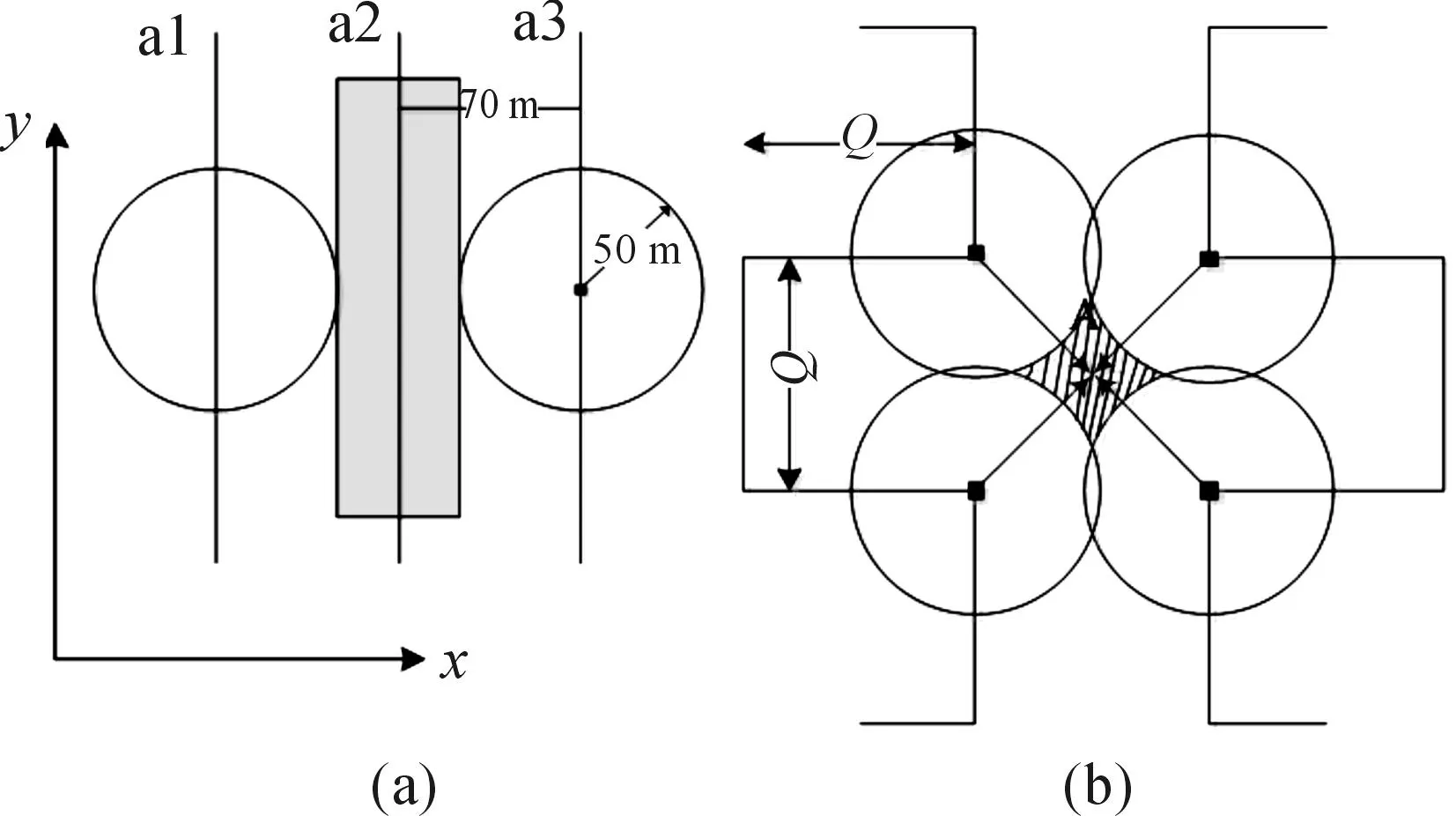
图3　节点与移动信标的通讯距离

2.3仿真实验结果

2.3.130 m分辨率

首先在480 m×480 m的区域内仿真高分辨率的轨迹。图4(a)～图4(d)分别是SCAN和HILBERT路径上传感器节点散布图和误差分布图。图4(e)为平均定位误差， SCAN为0.78 m，HILBERT为2.07 m。因为30 m的分辨率比40 m的传输范围小，每个节点都可以接收到强度高的信号，与PDF表中的数据能够很好地一一对应。此外，HILBERT轨迹的总定位误差是SCAN轨迹的2.6倍。因为HILBERT轨迹的自身缺点，即信标不会移动到传感器部署区域的边界上，所以在分辨率大于通信范围的情况下，这一因素就会很明显的影响到HILBERT轨迹的定位误差。

图4(a)为移动信标在30 m分辨率下的SCAN移动轨迹，图4(b)为SCAN移动轨迹下节点位置误差分布，图4(c)为移动信标在30 m分辨率下的HILBERT移动轨迹，图4(d)为HILBERT移动轨迹下节点位置误差分布,图4(e)为30 m分辨率下的定位误差，图4(f)为30 m分辨率下定位误差的概率分布函数。

图4(d)中，SCAN轨迹的定位误差的累积分布函数(CDF) 在1 m以内有一个很陡的直线上升区，误差大于1 m后几乎是水平的，说明在仿真中SCAN轨迹定位具有良好的一致性和很高的精度。此外，超过97%的节点的误差小于1 m，误差超过1 m的只有两个节点，分别为11.8 m和20.2 m。此误差分布和Sichitiu等人在文献[8]中信标随机移动的定位误差分布相似。从HILBERT轨迹的CDF可以看出其误差分布比SCAN的误差分布大，约93%的误差分布在2 m以内。

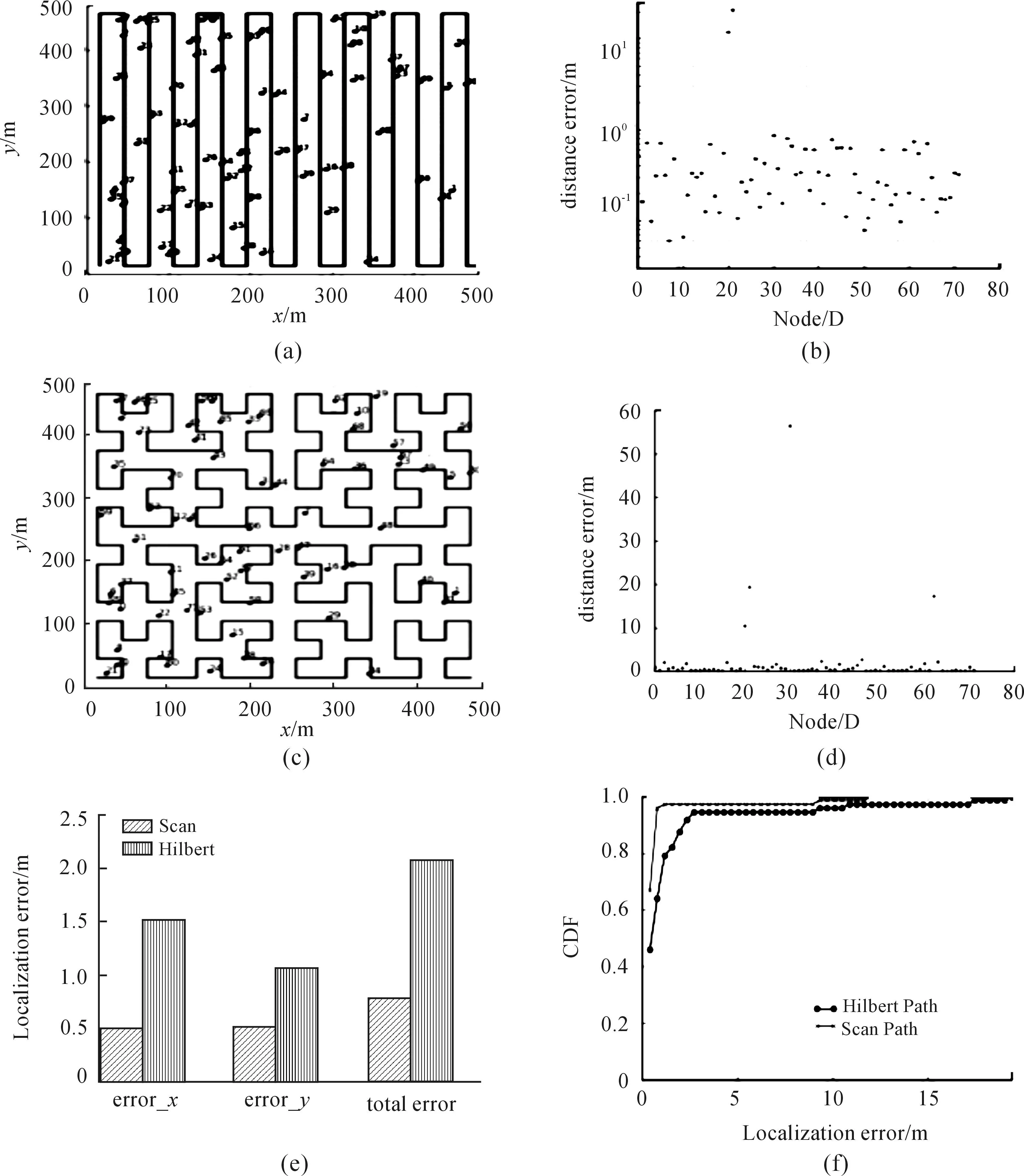
图4　SCAN和HILBERT路径上传感器节点散布和误差分布

2.3.250 m分辨率

对比图4(a)和图4(e)可知，增加分辨率会影响定位误差的绝对值。HILBERT和SCAN轨迹的平均定位误差分别增加了35%和115%。相比前一种情况，信标并没有从靠近节点的地方通过，因此传感器节点接收到的很多信号的信号强度很弱，会有更大的标准偏差。

如图5(a)所示，在50 m分辨率下，SCAN轨迹的定位误差比HILBERT轨迹定位误差小40%。在SCAN轨迹中，大多数节点仍然能够从两个方向接收到信号(左边和右边)，所以有91%的节点的定位误差在1 m以内。但是由于分辨率的增大，距离信标较远处的点在距信标最近位置上接收到信号强度减小，信号强度与距离映射的偏差就会加大。该节点再次接收到信号(信标远离时)确定的距离的误差就会更大，以此定位的误差也就增大了。这一因素对HILBERT轨迹定位性能有同样影响。对于处在最不利位置的传感器，在SCAN轨迹上它们能接收到信号的最近距离是25 m，而在HILBERT轨迹中是35.35 m。这一点上SCAN比HILBERT性能好。

图5(b)显示SCAN 和HILBERT的累积分布函数几乎是一样的。SCAN的曲线稍微高一点，其定位误差分布范围更小，定位精度更高。

图5　50 m分辨率下的定位误差及其概率分布

2.3.375 m分辨率

图6(a)显示了两个轨迹的定位误差结果。本次仿真中分辨率为75m，大于信号传播范围。SCAN和HILBERT两个轨迹的定位误差相比于50 m分辨率下的定位误差分别增加了约2.5倍和3.5倍。

与30 m和50 m两个分辨率不同， SCAN轨迹在70 m的分辨率下，大约52.6%的节点(206个节点)从一个线段(一个方向)上接收到信号(共线信号)，图4(a)解释了这个现象。图中展示了SCAN轨迹的3个线段：a1、a2和a3。a1和a2之间的距离以及a2和a3之间的距离是70 m，等于所选择的分辨率。在附近且位于阴影区域的任何节点只能接收到来自线段上的信号。因为它与其他两个线段的距离比50 m 的信号传输距离大。总之，对于每一个与y轴平行的轨迹线段，位于该线段两边20 m区域内的节点只能接收相应线段上的信号，因为该区域内的节点到第二条线段的距离大于信号传输距离50 m。这些区域所涵盖的总面积是16×40 m×1 200 m=768 000，如果除以总面积1 200 m×1 200 m=1 440 000，则占比为53.33%。当信标在y方向上移动，由于信号共线，位于这些区域中的节点的位置估计会有两个x坐标值，增加了x方向上的误差。

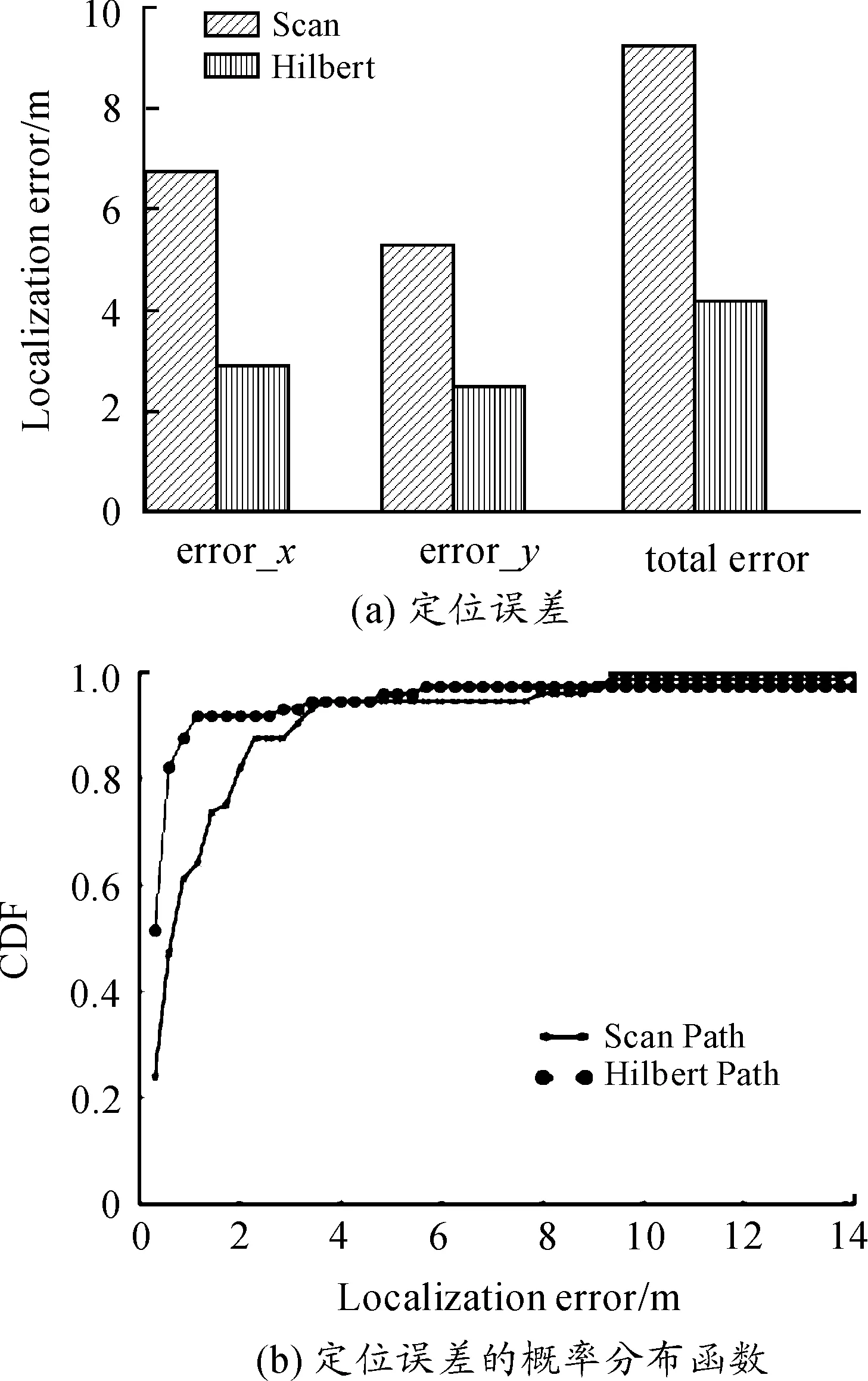
图6　75 m分辨率下的定位误差及其概率分布

由于很大比值的节点在轨迹SCAN上只接收到共线信号，影响定位误差的主要因素从节点与移动信标间的距离转移到了信号的共线性上。因此，现在SCAN轨迹总的定位误差比HILBERT轨迹约大57%，因此，后者具有最佳性能。

图6(b)显示了HILBERT和SCAN轨迹的定位误差累积分布函数。在此图中，注意到HILBERT轨迹在大部分区域累积分布函数比SCAN轨迹的好，但是最大误差值会降低其整体定位效果。在HILBERT轨迹上最大误差大约是64 m，但是SCAN轨迹的最大误差只有28 m。HILBERT轨迹比SCAN有更大的误差，是因为后者比前者提供更均匀的覆盖。对于位于这些由HILBERT曲线引起的“孔”中的节点，在HILBERT轨迹的70 m分辨率下，有一些无法控制的状态。其中一个状态如图4(b)所示。在此图中，节点A位于一个边长为70 m的矩形中心，距离它最近的4个信标的轨迹点分别是4个圆的圆心。虽然移动信标确保位于四个圆心点上时一直传输信号，但是节点A到这四点每个点的距离是53 m，大于传输距离。在这一确定的路径上，阴影范围内的节点将无法收到任何信号。由于信号传播过程中的衰减、反射、散射等随机性因素，这些跟A相似的节点实际上可以接收到部分信号，这些信号在PDF映射表中对应的距离具有很大的误差。仿真实验中只有很小比值的这样位置的传感器节点(只有8%或者392个里面有31个)，它们的定位误差均超过36 m。这是因为HILBERT轨迹中有较多的弯道，移动信标可以覆盖到整个节点部署区域，大多数节点可以从至少两个方向接收到信号，平均误差更小。因此，在分辨率较大(大于通讯距离)时的轨迹上，HILBERT轨迹的平均定位精度更高。

2.3.430 m分辨率下的不同速度

前几组仿真试验研究了信标速度一定的情况下不同分辨率下两个轨迹的定位性能，这组仿真研究在相同分辨率下不同速度对两个轨迹定位性能的影响。设定轨迹分辨率30 m，节点散布区域480 m×480 m，节点个数72个，速度分别为1 m/s，2 m/s，4 m/s和6 m/s。结果如图7所示。

图7　信标在不同速度下两个轨迹的定位误差

SCAN轨迹在4个速度下的平均定位误差分别为0.65 m，0.75 m，1.23 m和2.55 m。由图7中曲线可看出速度小于某一阈值(图中4 m/s左右)时，速度变化对误差影响不大，大于这个值时，速度的变化将引起误差很大的变化。因为信标在轨迹的一条线段上移动的距离一定，速度越小，其在这段距离上广播的信息就越多，线段附近的节点就会接收到更多的信息，RSSI的误差就会减小，进而提高节点位置的估计精度。

信标的移动速度变大也会引起HILBERT轨迹的定位误差变大，但是因为HILBERT轨迹有更多的弯道，信标会经过一个区域多次，所以速度对其定位误差影响是平缓的，如图7所示。因此合适的信标移动速度很有必要，低速可以提高定位精度，但是会花费更多的时间，而且速度低于某一阈值后误差随速度变化不明显。

3结论

一个确定的轨迹可以显著降低定位误差，还可以保证所有传感器节点可以获得位置估计。文中两个确定性轨道之间的比较表明， 当轨迹的分辨率小于或等于信号传输范围时，SCAN轨迹比HILBERT的误差略小，但是在分辨率远大于通讯范围时，HILBERT的性能明显优于SCAN轨迹。因此，要求信标遍历一个分布密度较小的节点部署区域，而又有能源或者运动表面限制(例如，许多障碍可能不允许一个非常密集的轨迹)，在这种情况下，HILBERT轨迹就很有用处，而且合适的信标移动速度对轨迹的定位性能有很大影响。

由于风、动物等外界因素的影响，传感器节点可能有一定的移动。因此下一步的工作主要是研究传感器节点移动的情况下移动信标最优路径的规划。

参考文献：

[1]屈峰.无线传感器网络及其应用[J].四川兵工学报，2013,34(2):111-113.

[2]段渭军.无线传感器网络节点定位系统与算法的研究和发展[J].信息与控制,2006,35(2):239-244.

[3]HE T.Speed:A stateless protocol for real-time communication in sensor networks[C]//Proceedings of ICDCS.[S.l.]:[s.n.],2003.

[4]钟智.具有移动节点的无线传感器网络定位算法和数据收集协议研究[D].长沙：中南大学,2012.

[5]PATHIRANA P N,BULUSU N,SAVKIN A V,et al.Node localization using mobile robots in delay-tolerant sensor networks[J].IEEE Trans.Mobile Comput.,2004(4):285-296.

[6]GALSTYAN A,KRISHNAMACHARI B,LERMAN K,et al.Distributed online localization in sensor networks using a moving target[C]//Proceedings of IPSN.[S.l.]:[s.n.],2004.

[7]PRIYANTHA N B,BALAKRISHNAN H,DEMAINE E,et al.Mobileassisted localization in wireless sensor networks[C]//Proceedings of IEEE INFOCOM.[S.l.]:[s.n.],2005.

[8]SICHITIU M L,RAMADURAI V.Localization of wireless sensor networks with a mobile beacon[C]// Proceedings of MASS.[S.l.]:[s.n.],2004.

[9]HU Y C,JOHNSSON S L.Data parallel performance optimizations using array aliasing[C]//Algorithms for Parallel Processing.[S.l.]:[s.n.],1999.

[10]LUO C,YANG S X.Complete coverage path planning with designated starting and planning locations using a neural network paradigm[C]//Proceedings of Eighth International Conference on Neural Information Processing.[S.l.]:[s.n.],2001.

(责任编辑杨继森)

Path Planning of Mobile Beacon in Wireless Sensor Network Node Localization

ZHANG Qiang1, ZHANG Qing1, ZHANG Lei2, YU Ji-yan1, JIA Fang-xiu1

(1.National Defense Key Laboratory of Ammunition Technology, Nanjing University of Science & Technology, Nanjing 210094, China; 2.Military Research and Development Center,Yuxi Industries Group Co., Ltd., Nanyang 473000 Luoyang, China)

Abstract:Two kinds of determined path (SCAN track and HILBERT track) were studied separately. It’s shown by the Enthought Canopy software simulation results that any definite beacon moving path which covers the entire region has a distinct advantage over the random moving path. When the node network area is traversed by moves beacon with the communication range which is less than the resolution, the SCAN path has a lower localization error. When the track is greater than the resolution of communication range, the HILBERT trajectory provides a higher accuracy significantly.

Key words:wireless sensor network; mobile landmark; node localization; path planning

文章编号：1006-0707(2016)02-0144-06

中图分类号：TP393

文献标识码：A

doi:10.11809/scbgxb2016.02.035

作者简介：张强(1988—)，男，硕士研究生，主要从事智能弹药和无线传感器网络技术研究。

收稿日期：2015-08-26；修回日期：2015-09-10

本文引用格式：张强，张庆，张磊，等.无线传感器网络节点定位中移动信标的路径规划[J].兵器装备工程学报，2016(2):144-149.

【信息科学与控制工程】