高转速弹丸姿态解算方法研究

邱海迪，李　嘉，牛春峰，李　岩

(1.南京理工大学 能源动力工程学院,南京　210094；

2.辽沈工业集团有限公司 研发中心设计二所,沈阳　110045；

3.中国兵器工业导航与控制技术研究所 弹箭与制导武器研究室,北京　100089)



高转速弹丸姿态解算方法研究

邱海迪1，李嘉2，牛春峰3，李岩1

(1.南京理工大学 能源动力工程学院,南京210094；

2.辽沈工业集团有限公司 研发中心设计二所,沈阳110045；

3.中国兵器工业导航与控制技术研究所 弹箭与制导武器研究室,北京100089)

摘要：针对传统利用三轴磁阻传感器测量姿态角的解算方法计算量大这一问题，根据常规高转速弹丸在飞行过程中偏转角变化小这一特点，提出了一种基于偏转角的计算方法，计算结果既保证了姿态角的解算精度，又减少了计算量，表明了此解算方法的可行性。

关键词：弹丸姿态解算；偏转角；三轴磁阻传感器；高转速弹丸

Citation format:QIU Hai-di, LI Jia, NIU Chun-feng,et al.Research on Attitude Algorithm for Projectile with High Spinning Speed[J].Journal of Ordnance Equipment Engineering,2016(2):7-10.

在现代化战争中，随着现代科学技术如微电子技术和传感器技术的快速发展及这些技术在武器上的应用[1-2]，各种常规弹药的智能化，灵巧化，精确化，高效毁伤成为弹药发展的方向之一。常规弹药制导化，既减少了战场弹药的消耗，又降低了战争的成本。而对姿态信息的探测是发展弹药制导化的关键[3]。常用的姿态测量传感器主要包括陀螺仪、加速度计、地磁传感器等[4]。在地球磁场作用下[5]，地磁传感器能够反映弹体飞行姿态的变化，因此地磁测姿技术得到了发展，地磁测姿技术具有低成本、隐蔽性好、抗冲击/全天候，无源且没有诸如陀螺等惯性器件的误差累计等诸多优点，因此使用磁传感器测量姿态逐渐成为姿态测量的热点方法之一。

文献[6,7]提出解算方法都需要确定某个初值，而在设定初值时存在一定的盲目性，往往解算出来的值与方程组的最优解存在较大误差，以往需要多次校对才能得到较准确的解，又无疑加大了工作量[8]。本文利用偏航角在高转速弹丸飞行过程中变化小的特点，提出了基于初始偏航角迭代计算的方法，并通Matlab仿真计算分析，结果既保证了解算精度，而且有效地减小了工作量。

1弹丸姿态解算数学模型

本文用到的3个坐标系分别为地面坐标系Axyz、弹体坐标系Ox1y1z1、大地坐标系OXYZ。

文献[9]给出了地面坐标系绕弹体的俯仰角ϑ、偏航角φ、倾斜角(滚转角)γ旋转至弹体坐标系的转换关系：

(1)

其中

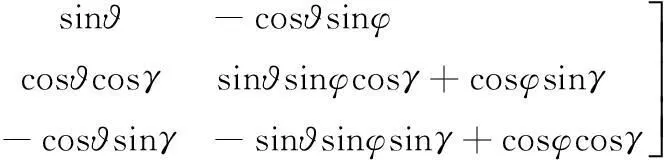
在观测点建立大地坐标系来描述地磁场的特征[10]。如图1所示，其中α为地面坐标Ax轴与正北方向(OX轴)的夹角，向东偏为正方向可得地面坐标系与大地坐标系间的转换关系为

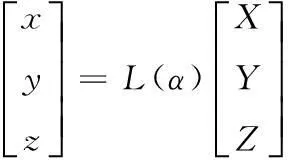
(2)

其中

由式(1)、式(2)得到大地坐标系与弹体坐标系的转换关系为

(3)

安装磁阻传感器时将其三轴与弹体坐标系的三坐标轴重合，此时磁阻传感器三轴测量的磁场大小，即为地磁场在弹体坐标系三轴上的投影。由式(3)可推得磁阻传感器三轴的测量磁场大小为

(4)

式(4)为解算弹丸姿态角的矩阵方程。其中Hx1、Hy1、Hz1为弹体坐标系下地磁场分量即三轴磁阻传感器测量值；HX、HY、HZ为地磁场在地磁坐标系三轴上的分量，根据测量地点的位置可以查地磁模型确定其值；α角在弹丸发射时是确定的。其中俯仰角、偏航角和滚转角的定义域分别为(-90°，90°)、(-180°，180°)和(0°，360°)。

图1　地面坐标夹角图

2姿态解算方法

为简化计算作如下假设：磁阻传感器无安装和测量误差；忽略弹体和电子器件对地磁的影响；地磁场在测量空间内保持不变。

将式(4)进行变换得：

Hx1= [(HXcosα+HZsinα)cosφ+

(HXsinα-HYcosα)sinφ]cosϑ-HZsinϑ

(5)

Hy1·sinγ+Hz1·cosγ=(HXcosα+

HYsinα)sinφ+(HYcosα-HXsinα)cosφ

(6)

式(5)和式(6)中由前一节已知除3个姿态角外，其他变量的值已确定，只要偏转角φ的值已知，即可由反三角函数求得俯仰角ϑ和滚转角γ。由于偏航角在弹体飞行过程中变化很小[7]，所以每次计算时可以将偏转角看为定值进行计算。假设弹丸发射时偏转角为φ0，代入到式(5)和式(6)中得ϑ0和γ0。将得到的3个姿态角ϑ0、φ0、γ0代入式(4)中算出此时姿态角对应的地磁场在弹体坐标系的投影大小：

(7)

(8)

解算过程的截至条件为算出的地磁场在弹体坐标系的投影与磁阻传感器测得的值一致。定义误差ε，用该误差表示弹体坐标轴磁场分量计算值与真实值之间的逼近程度。计算公式如下：

(9)

3仿真计算结果与分析

世界地磁模型(The World Magnetic Model，简称WMM)，每5年由NGDC(the National Geophysical Data Center)代表NGA(the United States’ National Geospatial-Intelligence Agency)发布1次，最近发布的模型到2019年12月31日到期。测试地点假设为南京，其地理位置为北纬32.028°，东经118.854°，海拔高度24.03 m，由世界地磁模型查得该地的地磁要素，查询结果为HX=32 827.3、HY=-3 153.2、HZ=37 268.2。基于解算方法的特点，后面主要分析偏转角步长和偏转角大小对解算结果的影响。

3.1步长选取对求解影响

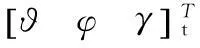
从表1可以看到：步长为0.001°、0.005°和0.01°时姿态角的解算值与真值误差的绝对值之和小于0.25°，与文献[8]中在该假设的弹体姿态时的解算结果相比误差小，而且计算次数也缩短很多；步长为0.02°时，解算误差较大，计算次数与其他3个步长相比计算量大，所以此步长选取不合适。步长取0.01°时，计算步骤最少，解算结果误差较小。

为了验证解算方法的可行性，另外做了3组解算，步长取0.01°，得到的结果如表2。由表2可以看出利用本文的计算方法计算出的3组结果都比较好。第一组的解算误差最大，但3个姿态角误差的绝对值之和小于0.4°，精度仍然比较高，结果证明所采用的解算方法具有一定的可行性。

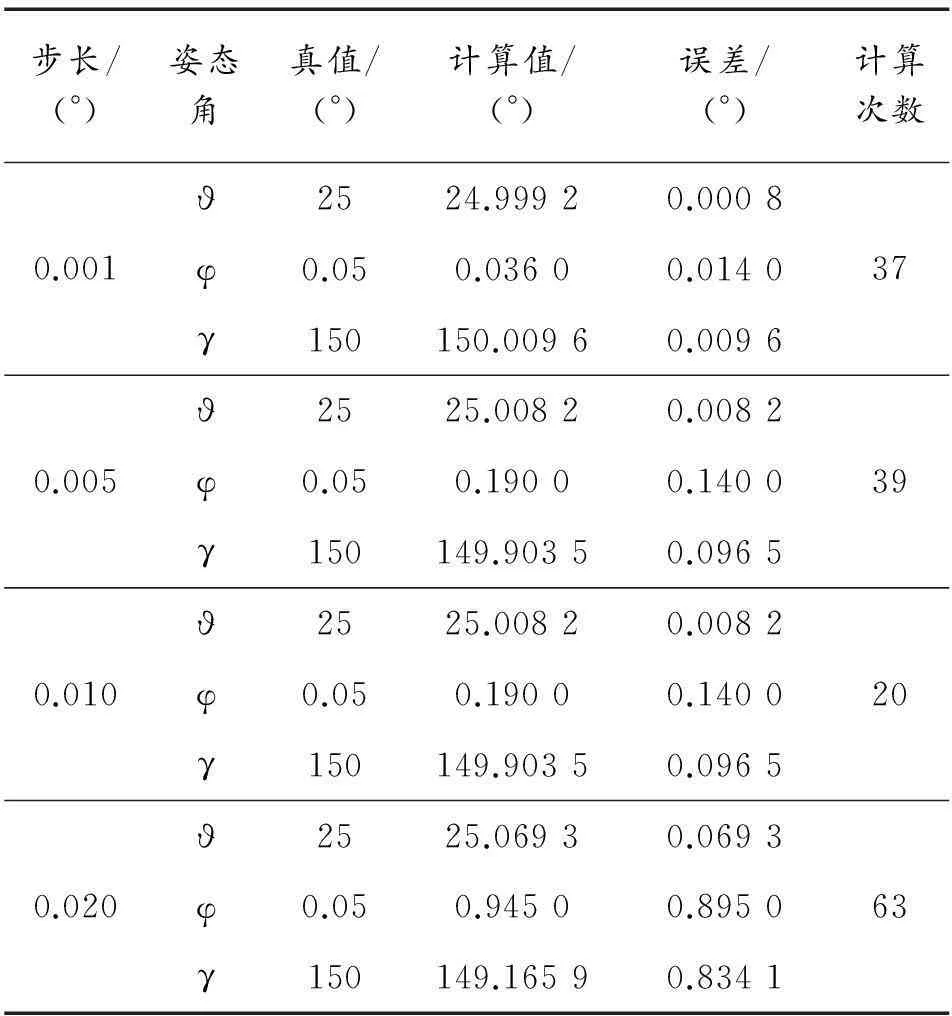
表1　偏转角φ不同步长的解算结果

表2　不同姿态角姿态角解算结果

3.2偏转角对解算结果的影响

本文中提出的解算方法是基于弹体在飞行过程偏航角较小的特点进行计算，这个小节分析了偏航角大小变化对解算精度的影响。假设弹体的俯仰角ϑ与滚转角γ为25°和150°，偏航角φ由0°增加至20°，探究偏航角大小对解算结果的影响。通过Matlab对3个姿态角仿真结果如图2~图4左图所示，横轴为偏转角大小，纵轴为3个角度解算值与真值的绝对误差。为了进一步分析数据，对原始数据进行拟合，得到图2~图4中的右图。

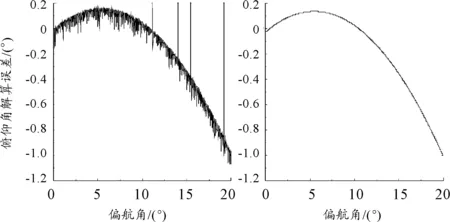
图2　俯仰角解算误差

图3　偏航角解算误差

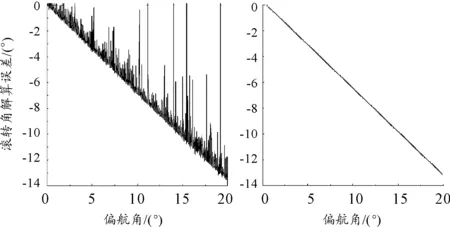
图4　滚转角解算误差

εϑ、εφ、εγ分别表示3个姿态角解算的绝对误差，式(10)为拟合后的函数表达式。其中ϑ角解算误差与φ角呈抛物线关系，φ和γ角解算误差与φ角呈线性关系。3条曲线拟合的可决系数R2分别为0.979 5、 0.962 7和0.962 4，都比较接近于1，数据拟合效果很好。

(10)

由图3可以看出偏转角φ的变化大小对ϑ角解算影响与另外两个姿态角相比要小很多，φ增加到20°时，解算误差仍在1°之内。假设要求3个姿态角的解算误差在0.5°以内，由(10)式可以计算出偏转φ的变化范围近似为(-0.03°，1°)。由以上结果也可以看出，在弹体偏转角很小时，姿态角解算误差较小，进一步说明此解算方法在小偏角时的可行性。

4结束语

本文基于磁阻传感器测量地磁分量的原理，针对常规高转速弹丸，提出以偏转角φ为计算基准的方法，对姿态角进行仿真计算，结果表明既保证了计算精度，还减少了计算量。

参考文献：

[1]RICE H,KEHNENSON S,MENDELSOHN L.Geophysical Navigation Technologies And Applications[J].IEEE PLANS,2004:618-624.

[2]ZHAO HAN-DONG.The Research about GPS applying to Rocket-Projectile[C]//Proceedings of the 5th International Symposium on Test and Measurement.2003:3269- 3272.

[3]杨绍卿.论武器装备的新领域——灵巧弹药[J].中国工程科学,2009(10):223-225.

[4]马国梁,李岩,葛敬飞.磁阻传感器测量旋转弹滚转姿态的原理分析[J].弹道学报,2012,24(1):32-36.

[5]邱荣剑,宓卉.基于地磁传感器的弹体姿态角测量方法研究[J].舰船电子工程,2012(11):97-99.

[6]海涛,曹咏弘,祖静.旋转弹姿态解算方法研究[J].兵工学报,2010,3l(7):987-990．

[7]QIN F J,LI A,XU J N.Design of attitude algorithm for 13-accelerometer based inertia navigation system[J].Journal of Chinese Inertial Technology,201l,19(6):637-641.

[8]高路鹏,狄长安,孔德仁,王桑.弹丸姿态解算方法研究[J].计算机仿真,2013(5):15-18.

[9]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M]．北京：北京理工大学出版社,2006.

[10]杨晓东,王炜.地磁导航原理[M].北京:国防工业出版社,2009.

(责任编辑周江川)

Research on Attitude Algorithm for Projectile with High Spinning Speed

QIU Hai-di1, LI Jia2, NIU Chun-feng3, LI Yan1

(1.School of Energy and Power Engineering, Nanjing University of Science & Technology, Nanjing 210094, China;2.No.2 Design Institute of Research & Development Center, Shenyang Industrial Group Co. Ltd.,Shenyang 110045, China; 3.Department of Guided Projectiles, Navigation and Control Technology Institute of China North Industries Group Cooperation, Beijing 100089, China)

Abstract:Traditional attitude algorithm with three-axis magneto resistive sensor needs large amount of calculation. In view of this problem, according to the deflection angle of conventional high spinning projectile varies little in process of flying, a kind of the algorithm method based on deflection angle was proposed. It not only ensures the calculating precision of the attitude angle, but also reduces the amount of calculation. The simulation results verify the feasibility of this calculating method.

Key words：projectile attitude algorithm; deflection angle; three-axis magneto resistive sensor; high spinning speed projectile

文章编号：1006-0707(2016)02-0007-04

中图分类号：TJ765.4

文献标识码：A

doi:10.11809/scbgxb2016.02.002

作者简介：邱海迪(1991—)，男，硕士，主要从事兵器工程研究。

基金项目：高等学校博士学科点专项科研基金资助课题(20113219120030)

收稿日期：2015-07-27；修回日期：2015-08-12

本文引用格式：邱海迪，李嘉，牛春峰，等.高转速弹丸姿态解算方法研究[J].兵器装备工程学报，2016(2):7-10.

【装备理论与装备技术】