采用改进蚁群算法的热工过程模型参数辨识

章程明， 张雨飞

(东南大学 能源与环境学院， 南京 210096)



采用改进蚁群算法的热工过程模型参数辨识

章程明， 张雨飞

(东南大学 能源与环境学院， 南京 210096)

摘要：在基本蚁群算法基础上引入人工免疫的思想，对算法中初始信息素分布、信息素调整机制及选择概率函数等方面做出改进，使蚁群辨识方法能够更快、更精确地逼近实际系统的输出。结合仿真实验结果表明，该方法比基本蚁群算法具有更高的寻优效率和辨识精度。

关键词：热工过程； 系统辨识； 蚁群算法； 人工免疫

电力生产系统结构复杂，系统之间强耦合，难以试验建模，至今没有普遍适用的控制传递函数模型[1-2]，根据现场运行参数直接求得热工过程的传递函数一直是控制领域研究的重要课题之一。近年来，群体智能(Swarm Intelligent)的快速发展及其在系统辨识中的应用，弥补了传统热工过程辨识方法的不足[3]。国内外学者对神经网络[4-6]、遗传算法[7-8]、粒子群算法[9]等群体智能算法在过程模型辨识的应用进行了广泛研究，其中蚁群算法作为一种模拟蚂蚁群体智能行为的仿生优化算法，采用正反馈并行自催化机制，具有较强的鲁棒性、优良的分布式计算机制、容易和其他方法相结合的特点，成为人们研究的热点算法之一[10-11]。然而由于基本蚁群算法前期信息素匮乏，求解初期过程耗时较长；算法迭代参数单一，信息素容易出现发散式增长，使求解后期陷入局部最优。

对此，笔者在基本蚁群算法中引入人工免疫的思想，利用其快速的全局搜索能力，产生蚁群算法在算法前期所需的初始解及初始信息素分布，避免盲目搜索，提高算法效率；同时通过抗体的多样性特征和自我调节的能力，调整信息素分布规律及扩散机制、改进概率选择函数，使算法能够及时跳出局部最优，快速向全局最优收敛，克服基本蚁群算法的缺陷。

笔者用组合优化的角度来看待热工过程模型的参数辨识问题，利用改进蚁群算法对所有可行解进行高效搜索，从而获得模型参数的最优估计。最后利用某循环流化床锅炉床压特性实验验证，得到了较好的辨识效果。

1基本蚁群算法

蚁群算法中的所有可行路径代表问题的所有可行解[12]。在开始时假设各节点上的信息素相等且为常数，即τi(0)=C。蚂蚁在前进中由节点处的信息素浓度选择路径下一节点。选择概率函数为：

(1)

式中：A表示待选择路径点的集合；τi(k)为第k次迭代中节点i的信息素强度；α为表示信息素重要程度的参数；η为启发因子；β为表示启发式因子重要程度的参数。所有蚂蚁完成一次循环后，各节点上信息素量根据下式调整：

(2)

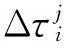
蚂蚁在完成每次搜索之后，按式(2)更新信息素矩阵。通过不断地循环迭代，最终找到全局最优解。

2蚁群算法的改进

改进蚁群算法的指导思想来源于人工免疫算法(Artificial Immune Algorithm，AIA)。它是一种根据生物免疫原理发展起来的新型智能随机优化算法，目前已经广泛应用在智能控制、模式识别等众多领域。

在人工免疫系统中，将被求解的问题看作是抗原，问题的解看作是抗体。算法从随机生成的初始解群出发，经过交叉、变异等人工免疫算子操作，产生新的子代抗体，循环迭代，使算法结果逼近最优解[13]。

2.1 改进初始信息素分布

基本蚁群算法中初始时刻各条路径上信息素相同，求解初期过程耗时较长。利用人工免疫算法快速的全局搜索能力，产生基本蚁群算法所缺乏的初始解及初始信息素分布，提高寻优效率。具体流程如下：

(1) 确定抗体集合。根据具体问题目标函数，将满足约束条件的所有解作为算法的抗体。

(2) 产生初始抗体。随机产生一批初始抗体，计算抗体与抗原之间的亲和力，剔除掉亲和力过差的抗体，同时生成新的抗体作为补充，重复以上操作，直到所有抗体都满足亲和力要求。

(3) 选择抗体。计算抗体浓度Ci，依次排除掉浓度最高的抗体，直到剩余抗体的个数满足要求。

第i个抗体的浓度Ci的计算公式为：

(3)

式中：Ci是第i个抗体的浓度；N是抗体集合中的抗体数目；aCij是与第i个抗体相似的抗体；aij是相似系数，当其值大于相似系数判别阈值μ时，则认为此抗体与第i个抗体相似，并取值为1，反之取0，相似系数判别阈值μ的取值是一定的[13]。

(4) 根据第3步得到的较优初始解生成信息素初始分布。

2.2 建立信息素分布调整机制

信息素分布是蚁群算法的核心，指导着算法结果向最优解逼近。然而基本蚁群算法没有对信息素的增长加以调整和约束，在正反馈机制的作用下，很容易使搜索陷入局部最优，出现算法停滞的问题。笔者引入人工免疫中的变异算子、交叉算子等操作，调整信息素分布，使其正确反映全局最优解的趋势。

2.2.1 交叉操作

当每一轮蚂蚁寻找路径结束后，对信息素矩阵进行交叉操作，即将当前最优路径节点上的信息素与同位置信息素含量最高的节点互换，从而确保下一次搜索对当前最优路径的搜索概率最大。

2.2.2 变异操作

对信息素矩阵特定节点进行变异操作，实现信息素的抑制与扩散，即对信息素矩阵同一列中信息素含量最高的节点进行抑制，防止信息素发散式增长，淹没其他节点被搜索到的可能，增大搜索的随机性；同时对此节点纵向邻域进行信息素扩散，实现对局部最优解的邻域搜索。

2.3 信息素扩散策略调整

为了使算法在前期有较强的全局搜索能力，加大发现全局最优解的概率，在后期能够加强局部搜索，以加快收敛速度，同时提高算法的精度，采用模拟退火策略，对各节点设置退火因子λi，即

中国科学院计算所汉语词法分析系统ICTCLAS采用层叠隐马尔可夫模型识别中文命名实体，系统设计了三级模型，低层粗切分，高层在低层结果的基础上精切分，每层都以隐马尔可夫模型作为基本算法，采用N-Nest 策略，将低层产生的最好结果送到高层，并为高层提供参数估计支持[3]。ICTCLAS 在2003 年5 月SIGHAN 举办的第一届汉语分词大赛中名列前茅。

(4)

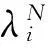
2.4 改进选择概率函数

在基本蚁群算法中，选择概率函数包含的参数过于单一，搜索过程很可能陷入局部最优。笔者在概率函数中融入抗体浓度的概念，加大了概率函数参数的多样性，使其更加全面地反映出全局信息。第k次迭代中选择概率函数为：

(5)

式中：τi(k)表示抗体所在的节点信息素；α是表示信息素重要程度的系数；ci表示第i个抗体的浓度；β是一个定值的常数。

3采用改进蚁群算法的热工过程模型辨识

3.1 热工过程辨识原理

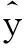
定义指标函数为：

(6)

3.2 热工过程模型结构

火电厂中绝大多数的热工过程都具有自平衡能力，并且属于多阶惯性环节，一般可认为其为具有纯延迟的高阶惯性对象，即

(7)

基于上述，共有四个未知参数：模型阶次n、增益系数K、时间常数T和迟延时间τ。模型辨识的过程就是寻找最优参数n、K、T、τ，使指标函数式(6)最小的过程。

4辨识仿真

4.1 仿真实例1

为了验证改进蚁群算法的有效性，在Matlab上对热工过程模型进行辨识，并和采用基本蚁群算法的参数辨识结果进行了比较。构造热工过程模型如下：

(8)

选取m=30，α=1.1，ρ=0.1，迭代次数为50，使用e(n)记录每次迭代辨识误差最小值，算法在迭代次数到达50或e(n)等于0就停止执行。模型参数选取范围为：K∈(-29.9，29.9)，T∈(0，199.9)，n∈(1，9)，τ∈(0，99)，其中，K和T的辨识精度为0.1，n和τ的辨识精度为1。

式(9)和式(10)分别为采用基本蚁群算法和改进蚁群算法的辨识结果：

(9)

(10)

式中：基本蚁群算法最终辨识误差e1为546.465 0，改进蚁群算法的最终辨识误差e2为9.122 8。

基本蚁群算法和改进蚁群算法的单位阶跃输出和实际输出对比见图2。结果表明：改进蚁群算法的单位阶跃输出和实际输出的拟合度更好。

基本蚁群算法与改进蚁群算法的辨识效果见图3。结果表明：由于改进了初始信息素分布，在算法初期辨识误差明显减小，且搜索后期没有出现停滞现象，改进蚁群算法比基本蚁群算法能够获得更小的辨识误差以及更精确的优化参数。

为验证算法的稳定性，对该对象重复进行了30次实验。图4为两种算法辨识效果的对比图。由图4可以看出：改进蚁群算法搜索到全局最优解的次数有12次，搜索概率为40%，且其他结果与最优解也很接近，基本满足工程实际需要；相比之下基本蚁群算法的搜索概率只有3%，其他搜索结果与全局最优解也相差甚远，效果不理想。由此表明：用改进蚁群算法进行目标参数辨识，辨识误差更低，误差波动范围更小，算法更加稳定。

4.2 仿真实例2

图5是300 MW循环流化床锅炉负荷在200～250 MW运行时，维持其他输入量不变，将一次风量阶跃增加16 km3/h，对床压的影响曲线。可以看出，当一次风量增加时，床压快速下降，整个下降过程时间约为60 s。

设定参数m=30，α=1.1，ρ=0.1，迭代次数为50。模型参数选取范围为：K∈(-0.499，0)，T∈(0，49.9)，n∈(1，5)。辨识精度设定同上。

基本蚁群算法辨识出的传递函数模型为：

(11)

辨识误差e1为2.518 4。改进蚁群算法辨识出的传递函数模型为：

(12)

辨识误差e2为0.867 1。

从以上仿真实例可以看出：与基本蚁群算法相比，利用改进蚁群算法对热工系统模型进行参数辨识，可以得到更好的辨识效果和更准确的热工模型。

5结语

笔者提出一种基于人工免疫的改进蚁群优化算法。该算法是在基本蚁群算法基础上引入人工免疫的思想，在算法初期利用人工免疫算法获得初始信息素分布，提高算法初期寻优效率；利用人工免疫算子与退火因子建立信息素调整与扩散机制，提高了算法的搜索效率与精度；将抗体浓度融入概率选择函数以更全面综合地利用全局信息，使算法进一步避免陷入局部最优。仿真实验结果表明：该方法克服了基本蚁群算法的缺陷，具有更高的寻优效率和逼近精度，在电厂热工过程参数辨识上具有一定的实用价值。

参考文献：

[1] 孙剑. 大型循环流化床锅炉燃烧系统特性与建模研究[D]. 北京：华北电力大学，2010.

[2] 郝勇生，于冲，吴波. 先进控制算法在热工控制中的关键问题研究[J]. 发电设备，2013，27(2)：101-104.

[3] 张洪涛，胡红丽，徐欣航，等. 基于粒子群算法的火电厂热工过程模型辨识[J]. 热力发电，2010，39(5)：59-61.

[4] 张栾英，李瑞欣，秦志明，等. 采用模拟退火算法的 Elman 网络及在热工过程建模中的应用[J]. 中国电机工程学报，2005，25(11)：90-94.

[5] 吴波，吴科，吕剑虹，等. 补偿递归模糊神经网络及在热工建模中的应用[J]. 东南大学学报：自然科学版，2008，38(4)：668-673.

[6] 米江，纪国宜. 基于改进BP神经网络的风机故障诊断研究[J]. 发电设备，2010，24(5)：430-434.

[7] 刘长良，于希宁，姚万业，等. 基于遗传算法的火电厂热工过程模型辨识[J]. 中国电机工程学报，2003，23(3)：170-174.

[8] 焦嵩鸣，韩璞，黄宇，等. 模糊量子遗传算法及其在热工过程模型辨识中的应用[J]. 中国电机工程学报，2007，27(5)：87-92.

[9] 韦根原，赵鹏旭，韩璞. 基于混沌粒子群算法的火电机组热工过程辨识方法[J]. 热力发电，2014，43(10)：35-39.

[10] 韦根原，朱波，马磊. 基于蚁群算法的热工系统模型辨识[J]. 计算机仿真，2014，31(1)：154-156.

[11] 何雅琴. 电厂热工过程参数辨识[J]. 计算机仿真，2015，32(2)：127-130.

[12] Bonabeau E， Dorigo M， Theraulaz G. Inspiration for optimization from social insect behavior[J]. Nature，2000，406(6)：39-42.

[13] 胡小兵，胡小平，黄席樾. 基于免疫原理的蚁群系统及其应用[J]. 数学的实践与认知，2006，36(6)：146-152.

Thermal Process Identification Based on Modified Ant Colony Algorithm

Zhang Chengming, Zhang Yufei

(School of Energy and Environment, Southeast University, Nanjing 210096, China)

Abstract：Based on the basic ant colony algorithm, the idea of artificial immune system was introduced to improve the initial distribution and adjustment mechanism of pheromones, and to optimize the selection probability function, so that the actual output of the system could be approached via ant colony identification method in a faster and more accurate way. Simulation results show that the method proposed has higher optimization efficiency and identification accuracy than the basic ant colony algorithm.

Keywords：thermal process; system identification; ant colony algorithm; artificial immunity

中图分类号：TK232; TP301.6

文献标志码：A

文章编号：1671-086X(2016)02-0077-04

作者简介：章程明(1990—)，男，在读硕士研究生，研究方向为热工过程自动化控制。E-mail: zcm1599@163.com

收稿日期：2015-09-02