增程式电动车BL和CD-CS型最优能量管理策略比较研究*

周 维，张承宁，李军求

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.北京理工大学，电动车辆国家工程实验室，北京 100081)

增程式电动车BL和CD-CS型最优能量管理策略比较研究*

周 维1,2，张承宁2，李军求2

(1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.北京理工大学，电动车辆国家工程实验室，北京 100081)

对增程式电动车两种典型能量管理策略下的最优控制效果进行了比较研究。通过构建新颖的控制模型和引入新型动态规划算法大大降低了最优能量管理问题的计算复杂度。不同工况和行驶距离下的仿真结果表明：1)混合(BL)型控制策略下最优SOC随行驶距离以近似线性的规律下降；2)BL控制下的油耗和电耗均比电量消耗-电量维持(CD-CS)型控制下的低，但差异不明显；3)BL控制能显著延长电池组的使用寿命。

增程式电动车；能量管理；最优SOC；比较研究；动态规划

前言

增程式电动汽车(EREV)在纯电动汽车的基础上增加一个小型辅助动力单元(APU)作为増程器，当动力电池电量不足时，増程器能配合动力电池一起为车辆行驶提供能源，因此，增程式电动汽车能有效解决现阶段纯电动汽车续驶里程不足的问题，被认为是新能源汽车向纯电动发展的重要过渡类型[1]。

与PHEV一样，EREV的能量管理策略大致可分两种：混合(BL)型和电量消耗-电量维持(CD-CS)型[2-4]。其中BL控制下，发动机可全程参与工作，配合电池一起为车辆行驶提供能源；而CD-CS控制下，发动机只在电池电量消耗到一定限值以下时才参与工作，在此之前，车辆一直工作在纯电动模式。目前工程上EREV的能量管理基本都采用CD-CS型控制策略，针对其研究也大多集中在CS阶段[5-6]，文献中还少有对BL和CD-CS两种控制策略进行对比研究的报道。因此，理清两者控制效果的差异对指导EREV能量管理策略的设计具有重要意义。

对多能源车辆能量管理控制的研究多基于最优控制理论进行，其中动态规划和庞特里亚金极小值原理是应用最为广泛的两种方法[7-8]。动态规划能保证获得全局最优解，但计算量大并需要提前预知整个行驶工况的信息，因此只适用于离线计算。庞特里亚金极小值原理计算量小，理论上能保证瞬时最优，且在满足一定条件的前提下也能获得全局最优的解[9]，被认为是最有可能在工程上实现的一种方法。由于本文的目的是对两种EREV能量管理策略进行比较，因此采用动态规划算法，以保证比较研究是在全局最优的基础上进行。

1 系统模型与能量管理最优控制问题的建立

1.1 系统模型与状态方程

本文中的研究对象是课题组与某汽车公司正在合作开发的增程式电动校车，其系统结构简图如图1所示。

能量管理控制的核心任务是实现直流母线上的需求功率Pbus在APU和电池组之间的合理分配，以保证在满足整车动力性的同时油耗尽可能低。能量管理是一个系统层面的控制问题，控制系统的采样时间取为1s[4,10]，因此建立系统模型时，快于1s的动态过程都可忽略而只保留相对较慢的动态。为有效处理APU的动态，同时保证动态规划算法能在有限的计算资源内完成计算，针对串联式构型中APU可以沿最佳燃油消耗曲线工作的特点(特别是对于EREV而言，由于电池组容量大，动态功率输出能力强，APU基本可以稳定地沿最佳燃油消耗曲线运行而不影响车辆的动力性)，本研究提出将APU输出功率作为状态变量而非控制输入。由于发动机起停对插电式车辆的节油效果具有较大影响，本文也将其作为一个状态变量进行优化。这样，与能量管理密切相关的状态变量有4个：车速v、APU输出功率Papu、发动机工作状态engstat(0表示停止，1表示工作)和电池荷电状态SOC。系统离散后的状态方程为

(1)

engstat(k+1)=engcmd(k)

(2)

Papu(k+1)=Papu(k)+δPapu(k)

(3)

SOC(k+1)=SOC(k)-

(4)

式中Fwh为车轮处的驱动力，各符号的意义和数值见表1。

表1 相关参数定义及数值

采用动态规划算法求解时，整个行驶工况的车速曲线已提前给定，因此车速可以被看成是外部输入的已知状态。通过式(1)可得到每一个时刻车轮的驱动力，进而根据当前时刻下的挡位信息和后功率链的工作效率，求得直流母线上的需求功率Pbus。需要指出的一点是，对本文中比较的两种能量管理策略，只要换挡时采用同样的策略，就不会影响最终的比较结果，因此为提高计算效率，本文未进行换挡策略的优化。式(2)是描述发动机起停控制的状态方程，其中engcmd表示发动机起停控制命令。对发动机起停过程做如下简化：假设起停均在1s内完成，在这1s的时间内，发动机由静止变换到怠速状态或由怠速变换到静止状态，APU不输出功率；发动机每次起动都会伴随一定的起动油耗。式(3)表示APU输出功率的状态方程；δPapu为APU功率变化率，是系统的一个控制变量，通过限制其变化范围(本研究中取[-11kW,11kW])，可保证APU的功率变化满足实际物理特性约束。式(4)是基于等效内阻模型得到的电池状态方程[4,7,10]，描述了SOC的动态变化；Rb和Voc分别为电池的内阻和开路电压，Pb为电池功率，可根据直流母线上的能量平衡关系得到：

Pb(k)=Pbus(k)-Papu(k)-PA

(5)

式中PA为电动化附件的功率。

1.2 发动机起动油耗的估算

发动机拖动起动是混合动力车辆提高节油率的一个重要功能。通常一个典型的拖动起动过程如下[11]：(1)发电机切换到电动模式将发动机从静止拖动到一定转速ne(通常为1 000r/min)，该过程中电池的电能损失将在未来由APU充电补充；(2)前2～3个循环，为使汽缸内和进气口形成油膜，保证发动机的可靠起动，需要加速加浓喷油(喷油量通常为怠速状态时喷油量的两倍以上)；(3)进入怠速状态。因此，起动油耗mf_s可由下式进行估算：

(6)

1.3 目标函数

将能量管理问题转化为一个最优控制问题，优化目标是使整个行驶过程中的总油耗最低：

(7)

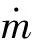
(8)

式中：N为整个行驶过程的时间步长；η(·)表示APU在最大效率曲线上的效率；mf_p是为防止发动机频繁起停影响乘坐舒适性和发动机寿命而引入的惩罚油耗。

1.4 初始和终端条件

对于BL型能量管理策略，为充分利用电池中储存的电能，最佳的控制策略是使SOC在旅程结束时达到所允许的最低限值(本文中取0.3)。发动机在开始和结束时都应保持在停机状态。因此BL控制下初始和终端状态为

(9)

而对于CD-CS型控制策略，当行驶距离在纯电动里程以内时，车辆工作在纯电动模式，无需进行优化。当SOC下降到一定限值(本文中取0.3)以下后，车辆进入CS阶段。在CS阶段，通常需要保持终端与初始SOC相等，以实现SOC有效维持：

(10)

1.5 系统约束条件

受制于部件的实际工作能力，系统应满足一定的约束条件，这些约束条件决定了系统状态变量和控制变量的可行域Φ和Ω：

(11)

(12)

式中：SOCmin和SOCmax在BL控制下分别取0.3和0.9，CS控制下分别取0.25和0.35；其余的约束边界在两种控制策略下均一致。

2 动态规划算法求解

以BL型能量管理策略为例，根据动态规划理论，当前时刻k下的最优控制输入为

L(k,x(k,i),u(k,i))}

(13)

式中：(k,i)对应k时刻下第i个状态；J(·)为从k+1时刻到终端时刻的累计油耗成本；L(·)为从k时刻到k+1时刻的转移油耗成本；x为系统的状态变量；u为系统的控制变量；*表示相应变量的最优解。

为保证终端约束(9)能被满足，通常令系统的抵达成本在目标终端状态处为0，而在其他状态处取一个极大的值：

(14)

算法的实现过程中，若在u(k,i)的作用下，k+1时刻的状态未落在离散状态点处，通常采用线性插值的方法来求从k时刻到k+1时刻的转移成本。显然，插值伴随着误差的产生(特别是在终端时刻两个相差巨大的数值之间插值)，且误差会从后往前传播和累积，这种现象在动态规划文献中被称为插值遗漏[12]。插值遗漏现象在本文的研究中尤其突出，主要原因是：(1)电池容量很大，导致SOC在每一个时间步长下的变化很微小，要捕捉到这个微小的变化，SOC就要离散得足够密，否则插值时会产生较大的误差；(2)为了保证仿真中车辆的行驶距离超过纯电动续驶里程，仿真时间必须设置得足够长，这样就会使插值误差在从后向前传播的过程中被放大。要减小插值遗漏的影响，就必须使状态空间的离散点数足够多，而这会大大增加计算负担甚至使计算无法完成。

为解决上述插值遗漏的问题，本文中引入一种基于逆向可达域的改进型动态规划算法[11]对最优能量管理问题进行求解，结果如图3所示。由于本文中研究的是一个终端固定的动态优化问题，所以只有从锥形区域以内的状态出发才能最终到达终端状态(即只有锥形区域内的状态才是逆向可达的)。所以，可考虑提前将逆向可达域找出来，而后在该区域内采用动态规划算法求解最优控制输入。

为区分状态空间内的逆向可达域和非可达域，定义如下函数：

(15)

而后，通过以下步骤计算状态空间内每一个状态的Lset值。

(1) 为使系统满足终端约束条件，令终端时刻的Lset值为

Lset(x(N-1))=max{(xf_min-x(N-1)),

(x(N-1)-xf_max)}

(16)

(2) 从0～N-2时刻，采用传统动态规划算法计算出每一时刻的Lset值。计算过程中，每一个时刻下的转移成本为零。

(3) 在Lset小于零即逆向可达域内采用传统动态规划算法求解最优控制输入。

3 仿真与结果分析

3.1 仿真工况设定

为研究不同循环工况和行驶距离对控制效果的影响，设计了表2中所列9种不同的组合工况，以覆盖城区、高速和复合工况下多种不同的工况特征以及短程、中程和远程3种不同的行驶距离。其中UDDS和US06工况的最高车速都被等比例缩小到目标车辆的设计最高车速80km/h。

表2 仿真中所用行驶工况

3.2 仿真与结果分析

3.2.1 部件最优状态曲线

各工况下BL和CD-CS两种控制策略分别对应的SOC曲线如图4所示(篇幅所限，只给出了其中4种典型工况下的情况，其他工况下的SOC曲线呈现出相同的特征)。由图可见，BL型控制策略下，不论工况类型和行驶距离长短，SOC总体上都随行驶距离(或位置)近似线性下降。文献[13]中也发现了相似的规律。这个规律对于设计实时最优的在线控制策略具有指导意义(比如通过GPS获取出发地和目的地之间的距离后，即可提前规划出电池SOC的参考曲线，而后通过合理控制APU和电池组之间的功率分配，使电池组沿参考SOC放电)。

图5和图6分别截取了一段工况4和工况7下各部件(APU、驱动电机、电池组)功率随时间变化的曲线。由图可见，BL控制时，APU只有在驱动电机需求功率很大的情况下才会投入工作，因为此时APU可以工作在其最大效率点上；当需求功率较小时，电池组单独提供功率，整个过程中几乎不存在APU给电池组充电的情况。CS控制下，为有效维持电池组的SOC在0.3附近，APU投入工作的程度要明显高于BL控制，而且很多时候会有APU在提供驱动功率的同时给电池组充电的情况，这种情况在工况7(高速工况)下特别明显，因为高速工况下高功率需求持续时间长，只有在需求功率较低时利用APU给电池充电，才能满足后期长时间的高功率行驶需求。

3.2.2 油耗和电耗比较

图7和图8分别比较了不同工况下BL和CD-CS两种控制策略所产生的燃油消耗和电能消耗。可以看到，无论对于何种工况，BL控制的油耗和电耗都比CD-CS控制的低，但两者之间的差异很小(油耗差别在1%～2%之间，电耗差别在1%以下)。

为分析油耗差别不显著的原因，图9以工况4为例，画出了APU在BL和CD-CS控制下的工作点分布情况。可以看到，两种控制策略下，APU工作点均沿其最大效率曲线分布，并且几乎是相互重合的。这是由于APU与车轮之间没有机械连接，无论采用何种控制策略，APU均能不受车轮处车速和负载约束，自由地工作在其效率最高的区间内。只是CS控制时，由于电池SOC较低，为维持SOC，APU在某些时候需要偏离其最大效率点，工作在负荷较大而效率次优的区间内，这也是CD-CS型控制下油耗比BL控制稍低的原因。而且油耗差异在电量维持阶段多为高速工况时相对较明显(工况3，5，7)，在行驶距离较长时相对较小(工况8，9)。图10和图11分别为工况4和工况7两种控制策略下APU功率分布直方图。由图可见：两种控制策略下，APU功率点均主要集中在65kW(最大效率点)附近；CS控制时，APU功率在65kW附近出现的频次要比BL控制时高，而且高速工况时(图11)，APU会很明显出现65～75kW之间的工作点，所以此时CD-CS和BL之间的油耗差别更明显。电耗差别随着电量维持阶段高速工况所占的比重提高而加大，因为高速工况下会伴随更多APU给电池组充电的情况(图6)，导致CS控制时电耗增多。

3.2.3 电池组使用寿命比较

一般认为，电池组在全寿命周期内能通过的充放电绝对安时数是大致一定的。因此，本文中采用累计绝对安时数Qcum对电池组的使用寿命进行定量评估：

式中I包括放电电流和充电电流。

图12计算了不同工况下采用BL和CD-CS控制分别得到的累计绝对安时数。可以看到，BL控制下电池组的累计绝对安时数明显比CD-CS控制低，说明BL型能量管理策略能大幅提高电池组的耐久性。这主要是由于BL型控制策略通过全程优化APU和电池组之间的功率分配，尽可能避免了APU给电池组充电的情况(由图9和图10可见)。而且，BL控制能通过APU的配合主动管理电池组的放电电流，这也能在一定程度上延缓电池组的老化。因此，通过设计合理的BL型能量管理策略，对于延长电池组的使用寿命很有帮助。

4 结论

(1) 对某增程式电动车两种典型能量管理策略的最优控制效果进行了对比分析。通过构建以APU功率变化率为控制输入的系统控制模型，并引入一种基于逆向可达域的动态规划算法，大大降低了最优能量管理问题的计算复杂度。

(2) 不同工况类型和行驶距离下的仿真结果显示，BL控制下的油耗和电耗均比CD-CS控制低，但差别并不明显。在CS阶段，高速工况时的油耗和电耗都比城区工况高。

(3) BL控制下，最优SOC随行驶距离近似线性下降。这个特征不受工况类型和行驶距离的改变而改变，因此对设计一种在线的BL型控制策略具有指导意义。

(4) BL控制下电池组的累计绝对安时数显著低于CD-CS型控制，且通过APU的配合，减弱了电池组的放电强度。表明BL控制有助于延长电池组的使用寿命。

[1] TATE E D, HARPSTERMICHAEL O, Savagian Peter J. The electrification of the automobile: from conventional hybrid, to plug-in hybrids, to extended-range electric vehicles[C]. SAE Paper 2008-01-0458.

[2] Wirasingha Sanjaka G, Emadi Ali. Classification and review of control strategies for plug-in hybrid electric vehicles[J]. IEEE Transactions on Vehicular Technology,2011,60(1):111-122.

[3] Karbowski Dominik, Rousseau Aymric, Pagerit Sylvain, et al. Plug-in vehicle control strategy: from global optimization to real-time application[C].Proceedings of the 22th International Electric Vehicle Symposium (EVS22), Yokohama, Japan,2006.

[4] Moura Scott Jason, Fathy Hosam K, Callaway Duncan S, et al. A stochastic optimal control approach for power management in plug-in hybrid electric vehicles[J]. IEEE Transactions on Control Systems Technology,2011,19(3):545-555.

[5] 胡明寅,杨福源,欧阳明高,等.增程式电动车分布式控制系统的研究[J].汽车工程,2012,34(3):197-202.

[6] 曲晓冬,王庆年,于远彬.增程式电动车的APU控制策略研究[J].汽车工程,2013,35(9):763-768.

[7] LIN Chanchiao, PENG Huei, GRIZZLEJESSY W, et al. Power management strategy for a parallel hybrid electric truck [J]. IEEE Transactions on Control Systems Technology,2003,11(6):839-849.

[8] Serrao Lorenzo, Rizzoni Giorgio. Optimal control of power split for a hybrid electric refuse vehicle[C]. Proceedings of the American Control Conference, Seattle, USA,2008.

[9] KIM Namwook, CHA Sukwon, PENG Huei. Optimal control of hybrid electric vehicles based on pontryagin’s minimum principle [J].IEEE Transactions on Control Systems Technology,2011, 19(5): 1279-1287.

[10] Cairano Stefano Di, LIANG Wei, KolmanovskyIlya V, et al. Power smoothing energy management and its application to a series hybrid powertrain[J]. IEEE Transactions on Control Systems Technology,2013,21(6):2091-2103.

[11] YU S E, OHN H S, MIN K D. Investigation of engine restart stability after idle stop for a mild type HEV powertrain[J]. International Journal of Automotive Technology,2013,14(5):683-692.

[12] Elbert Philipp, Ebbesen Soren, Guzzella Lino. Implementation of dynamic programming for n-dimensional optimal control problems with final state constraints[J]. IEEE Transactions on Control Systems Technology,2013,21(3):924-931.

[13] Sharma Oruganti Prashanth. A practical implementation of a near optimal energy management strategy on the pontryagin’s minimum principle in a PHEV[D].Master Thesis, The Ohio State University,2012.

A Study on Comparison Between BL and CD-CS Optimal EnergyManagement Strategies for Extended Range Electric Vehicles

Zhou Wei1,2, Zhang Chengning2& Li Junqiu2

1.HunanUniversity,StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,Changsha410082;2.BeijingInstituteofTechnology,NationalEngineeringLaboratoryforElectricVehicles,Beijing100081

The optimum control effects for extended range electric vehicles under two typical energy management strategies are comparatively studied. By creating novel control model and introducing new type of dynamic programming, the complexity of computation on optimum energy management issue is greatly lowered. The results of simulation for different driving circle combinations and driving distances indicate that: 1) under blended (BL) type control strategy, the optimal SOC approximately linearly lowers with the extension of driving distance; 2) The fuel and electricity consumptions under BL control are always slightly lower than those under CD-CS control; 3) The service life of battery can be notably extended with BL control.

extended range electric vehicles; energy management; optimal SOC; comparative study; dynamic programming

*中央高校基本科研业务费和北京市教委科技发展基金(20120339234)资助。

2016222

原稿收到日期为2014年12月31日，修改稿收到日期为2016年3月18日。