基于悬架行程解耦的SUV路面不平度识别算法研究
2016-04-11刘秋铮李素文
张 建,刘秋铮,王 康,刘 晔,李素文
(中国第一汽车股份有限公司技术中心汽车电子部,长春 130011)
2016193
基于悬架行程解耦的SUV路面不平度识别算法研究
张 建,刘秋铮,王 康,刘 晔,李素文
(中国第一汽车股份有限公司技术中心汽车电子部,长春 130011)
基于某SUV半主动悬架测得的悬架动行程信号,分析了几种典型工况的悬架动行程频域特性;设计了基于车辆加速度的悬架行程解耦算法,以消除车辆惯性力引起的悬架行程变化对路面不平度识别的影响;提出了以设定的车辆行驶距离内的悬架动行程积分为指标识别路面不平度的算法;最后进行了实车道路试验验证。结果表明,所设计的算法能有效辨识良好铺装路面和不平路面,且在车辆急加速,急制动和急转弯时不会造成误识别。
SUV;路面不平度识别;悬架行程解耦;悬架模型
前言
车辆行驶环境在线识别在现代汽车系统中越发重要。良好铺装路面和不平路面都是SUV的常用行驶路况,路面不平度的在线辨识是SUV路面识别系统的重要组成部分。由于路面不平度对车辆行驶性能的重大影响,国内外学者和汽车技术人员在路面不平度的识别方法上已经进行了大量的研究[1]。文献[2]中提出了一种基于悬架和车轮动行程的路面不平度识别方法,这一研究基于频域分析方法,辨识车辆以不同速度在不同路面上行驶时的路面颠簸。文献[3]中研究了一种在悬架上加装加速度计,从而进行路面不平度辨识并进行分类的方法,这一研究的辨识结果不受车速影响。文献[4]中提出了一种基于单轴激光探测和定位装置(laser detection and ranging,LADAR)的路面几何形状辨识方法。文献[5]中则设计了一种基于车轮垂直动载荷的路面不平度的识别方法。这些研究结果已经在不同条件下得到了验证,但是在实用化中仍存在各自的问题,本文中的研究目标是采用原车上已有的传感器信号设计实用化的路面不平度识别算法,为了能够适应SUV的恶劣多变的行驶工况,算法要同时满足实时性和精确性的要求,并且能够处理各种特殊工况。
因此,本文中以某高端SUV为目标车型,基于该车型上装备的半主动悬架所发出的悬架动行程信号开展研究,分析了几种典型工况下的悬架动行程频域特征,据此为消除车辆急加速、制动或转向时,簧载质量加速度引起的惯性力导致的悬架行程变化对路面不平度识别效果的影响,从实时性和准确性的角度分析了几种悬架模型的估算性能,选择合适的模型设计了悬架行程解耦算法;据此提出了路面不平度辨识指标,并进行了实车道路试验验证。结果表明,所设计的算法能兼顾实时性和精确性的要求,有效识别良好铺装路面和不平路面,且在车辆急加速、制动或转向时不会出现误识别。
1 悬架动行程信号频域特征分析
悬架动行程实质上是悬架系统在路面激励作用下的响应,虽然对于车辆系统而言,路面激励难以实时获取,但一般说来,不平路面的激励远大于良好路面,因此导致的悬架动行程也较大。目标车型是一种高端SUV,4个悬架均为半主动独立悬架,针对目标车进行了水平良好路面上匀速直行、不平路面直行、水平良好路面上蛇行以及水平良好路面上急加速+急减速的道路试验,测取了各工况下悬架的动行程,如图1所示。采用FFT方法进行悬架动行程的功率谱估计,结果如图2所示。
由图1可见,车辆在不平路面上行驶时悬架动行程远大于水平路面匀速直行工况,从图2中也可明显看出这一点,但车辆在良好路面上行驶且加速度较大时也会引起悬架大幅度波动,其功率谱密度在一定频段甚至高于不平路面的行驶工况。为了验证悬架动行程与车辆加速度的关系,对水平路面蛇行工况的悬架动行程和侧向加速度进行功率谱分析,结果如图3所示。由图可见,悬架动行程与侧向加速度在0.2Hz处均有很强的能量集中,说明此时悬架动行程与车辆加速度有很强的相关性。可以使用车辆加速度对悬架动行程进行解耦,分离出路面不平造成的悬架波动,从而进行路面不平度的识别。
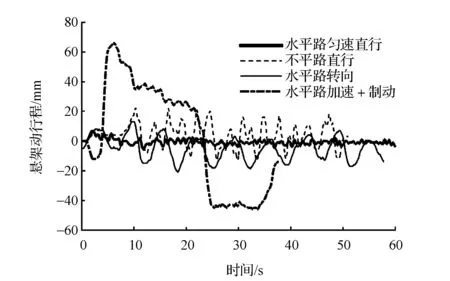
图1 不同工况下悬架的动行程
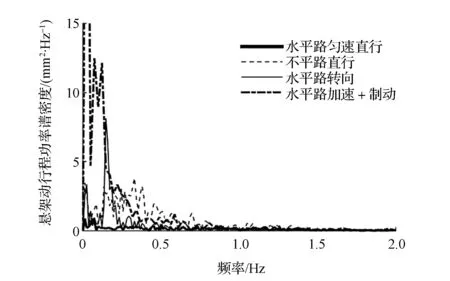
图2 不同工况悬架动行程的功率谱密度
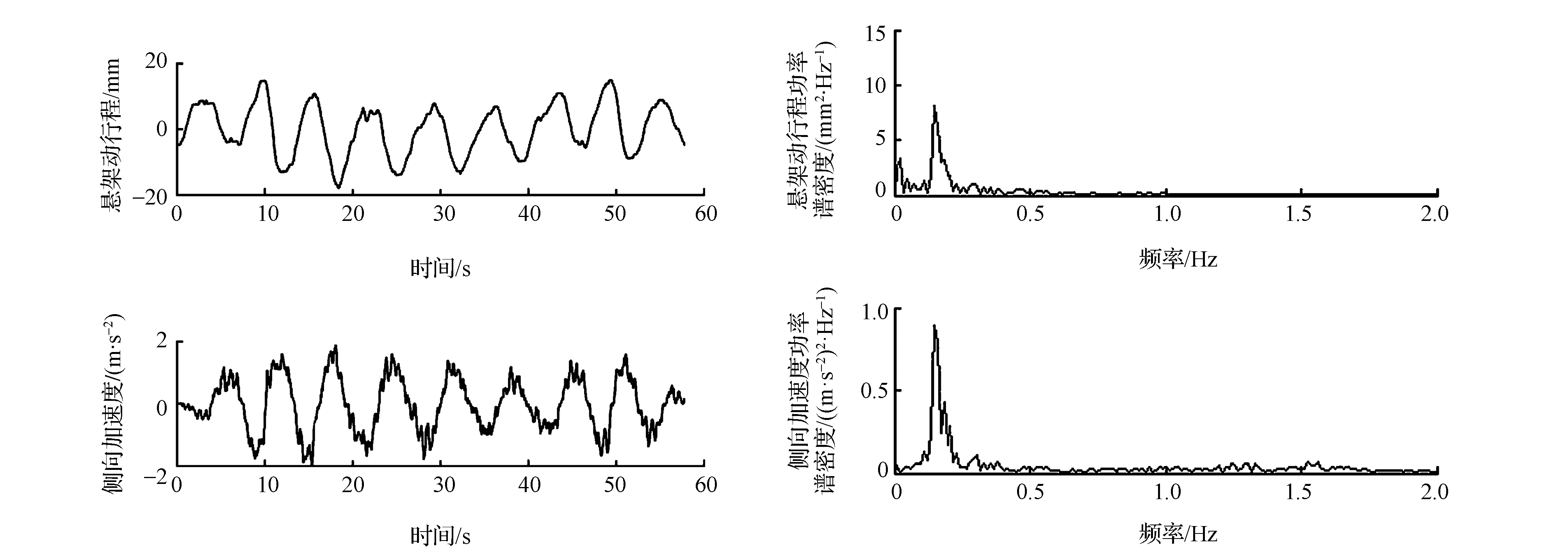
图3 水平路面蛇行工况悬架动行程与侧向加速度的频域关系
2 悬架动行程解耦算法
2.1 悬架动行程分解
在半主动悬架实测的悬架动行程中减去由加速度估算得到的动行程,即可得到由路面不平造成的悬架动行程,实现悬架行程解耦:
zsus=zmea-zcal
(1)式中:zmea为由半主动悬架发出的悬架行程测量值;zcal为车辆加速度造成的悬架动行程计算值。
解耦悬架行程zsus即可用于路面不平度识别。
2.2 车辆加速度造成的悬架动行程计算
悬架行程解耦所需的加速度导致的悬架变形zcal可采用车辆垂向运动动力学模型估算。考虑到车载控制单元的计算能力,需要对模型进行简化。由于当车辆悬挂质量分配系数接近于1时,可认为前后轴悬挂质量垂直运动相互独立[6],为有效反映车辆侧倾刚度对悬架动行程的影响,对前后轴分别采用1/2车辆振动模型计算悬架行程,模型如图4所示。
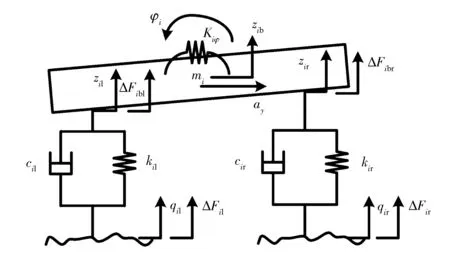
图4 1/2车辆振动模型
列出力和力矩平衡方程为
(2)
其中
zib=(zil+zir)/2,φi=(zir-zil)/B
1/2车辆模型将前后轴悬挂质量分别计算,其中i=f表示前轴,i=r表示后轴。
簧载质量mf和mr分别对应汽车前轴或后轴的
等效集中质量,即
(3)
ΔFil,ΔFir为单轴左右车轮车辆动载荷,用下式计算:
(4)
由于路面不平和车辆加速度分别会对悬架行程造成影响,而本文中也是分别对其进行考虑的,因此在估算车辆加速度造成的悬架动行程时,可以假设路面是完全平整的,即假设路面输入
qil=qir=0
(5)
式中:M为汽车总质量;m为整车簧载质量;mf,mr分别为前轴和后轴的等效集中质量;a为汽车质心到前轴距离;b为汽车质心到后轴距离;L为轴距;B为轮距;h为汽车质心高;e为簧载质量质心到侧倾中心的距离;g为重力加速度;cil,cir分别为单轴左、右悬架阻尼;kil,kir分别为单轴左、右悬架刚度;Kfφ,Krφ分别为汽车前、后轴的侧倾角刚度;φ为整车侧倾角;φi为汽车单轴侧倾角;zib为前后轴簧载质量垂向行程;zil,zir分别为单个车轴上车身在悬挂点处的垂向行程;ΔFibl,ΔFibr分别为单轴左、右悬架力;ax为汽车纵向加速度;ay为汽车侧向加速度。
不同整车装载质量和装载位置可能会对计算过程略有影响,但考虑到每次车辆行驶过程中两者的变化量一般较小,不会对估算结果有很大影响,因此本文中暂未考虑这一因素,假设车辆载荷状态不变。
2.3 悬架动行程计算算法验证
以左前悬架计算结果为例说明悬架动行程计算算法的效果。图5为蛇行工况下估计得到的悬架动行程;图6为急加速紧接急减速工况估计得到的悬架动行程,可见该算法的估算结果非常接近实测值。
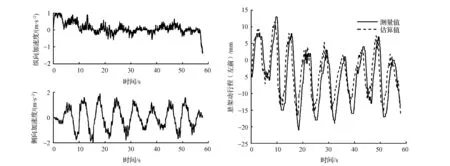
图5 水平路面蛇行工况悬架动行程计算
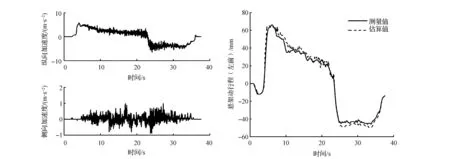
图6 水平路面急加速+急减速工况悬架动行程计算
3 路面不平度识别指标的确定
悬架行程解耦后,可以应用频域分析方法进行路面不平度的估计[7],但是功率谱分析方法计算量大,不适合用于在线计算,因此有必要从悬架动行程中找到能反映路面不平度特征的合适指标[8]。由图2可见,悬架动行程信息中,绝大部分能量都集中在1Hz以下,这一方面是由于悬架振动频率本来就较低,由半主动悬架发出的悬架动行程又是经过滤波处理后的信号,因此,可以用该信号的振动能量(也即是1Hz以下的低频振动能量)来估计路面不平度。
此外,悬架动行程的功率谱是时间谱,而路面不平度则是空间谱,需要考虑车速的影响。最后确定采用车辆每行驶1m的距离时,解耦悬架行程zsus的曲线与横轴(行驶距离S)所围成的面积Esus作为表征指标,如图7所示。
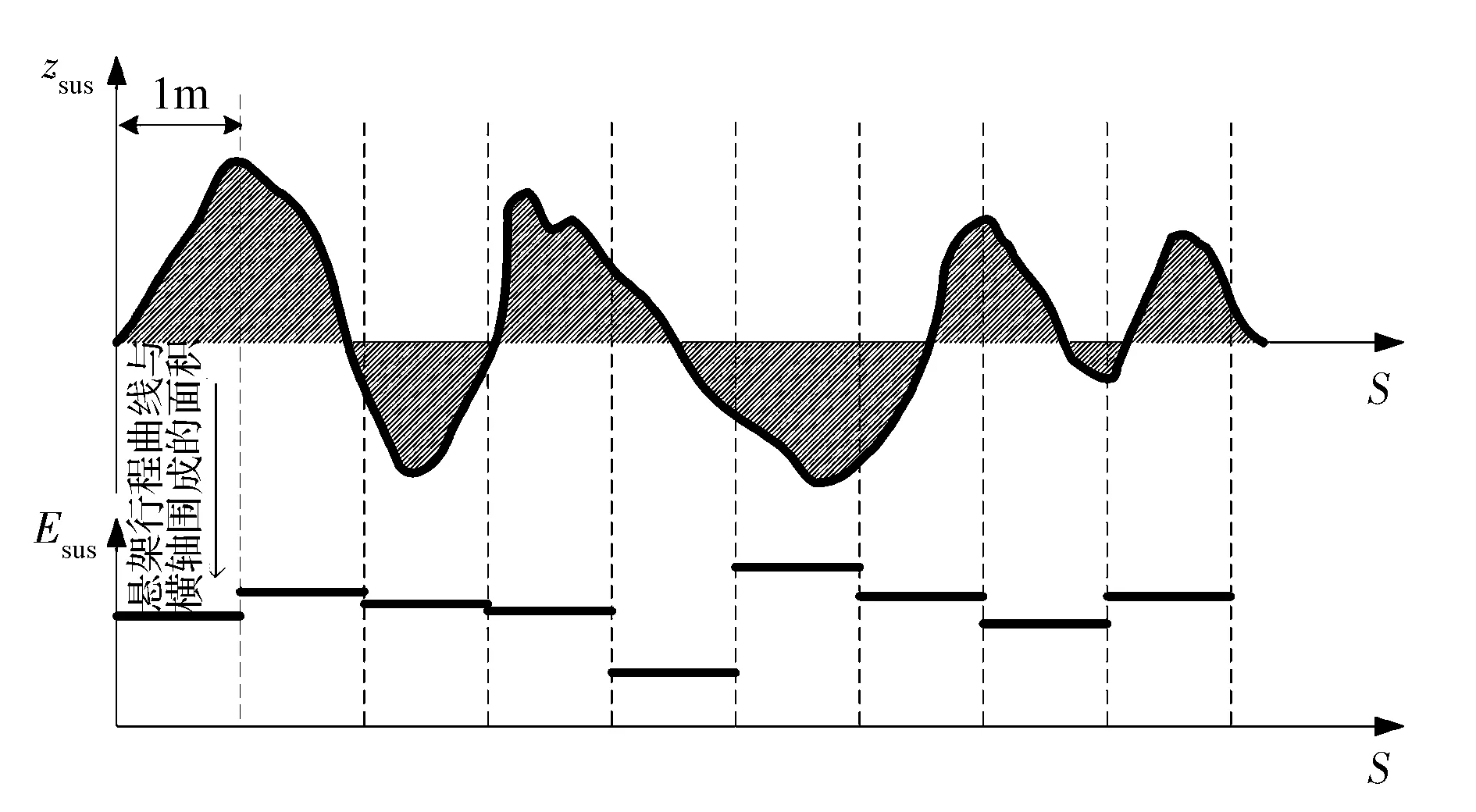
图7 路面不平度指标
4 道路试验研究
为验证算法的有效性,分别进行了水平良好路面上匀速直行、不平路面直行、水平良好路面上蛇行和水平良好路面上急加速+急减速的道路试验,试验结果如图8~图11所示。每个工况均以左前悬架动行程和路面不平度指标为例进行说明。
(1)图8为水平良好路面匀速直行工况的试验结果。试验车速为60km/h,可见车辆行驶平稳,悬架动行程很小,路面不平度指标接近于0。
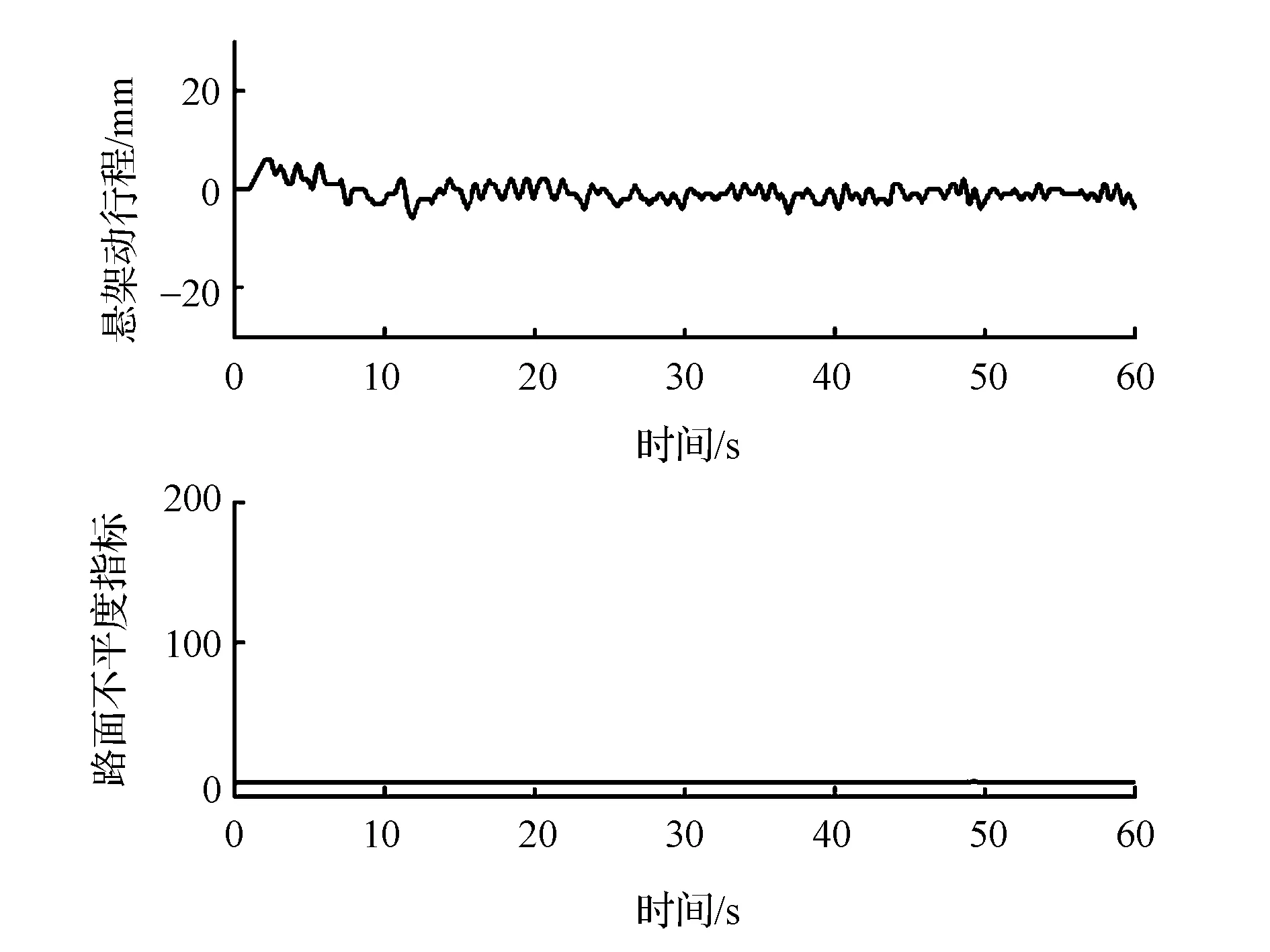
图8 水平良好路面直行不平度辨识结果
(2)图9为不平路面直行工况的试验结果。试验时在试验人员可承受的前提下保持尽量高的行驶车速,可见悬架动行程剧烈变化,路面不平度指标迅速上升,左前轮路面不平度指标最高可达180。
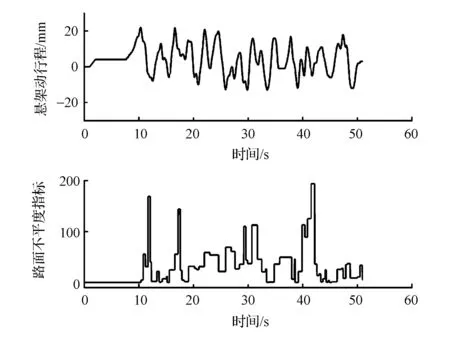
图9 不平路面直行不平度辨识结果
(3)图10和图11为水平良好路面蛇行工况及急加速+急减速工况的试验结果。可见大加速度导致大幅度的载荷转移,并将引起悬架动行程剧烈变化,此时路面不平度指标高于匀速行驶工况,但基本可以保持在5以下。
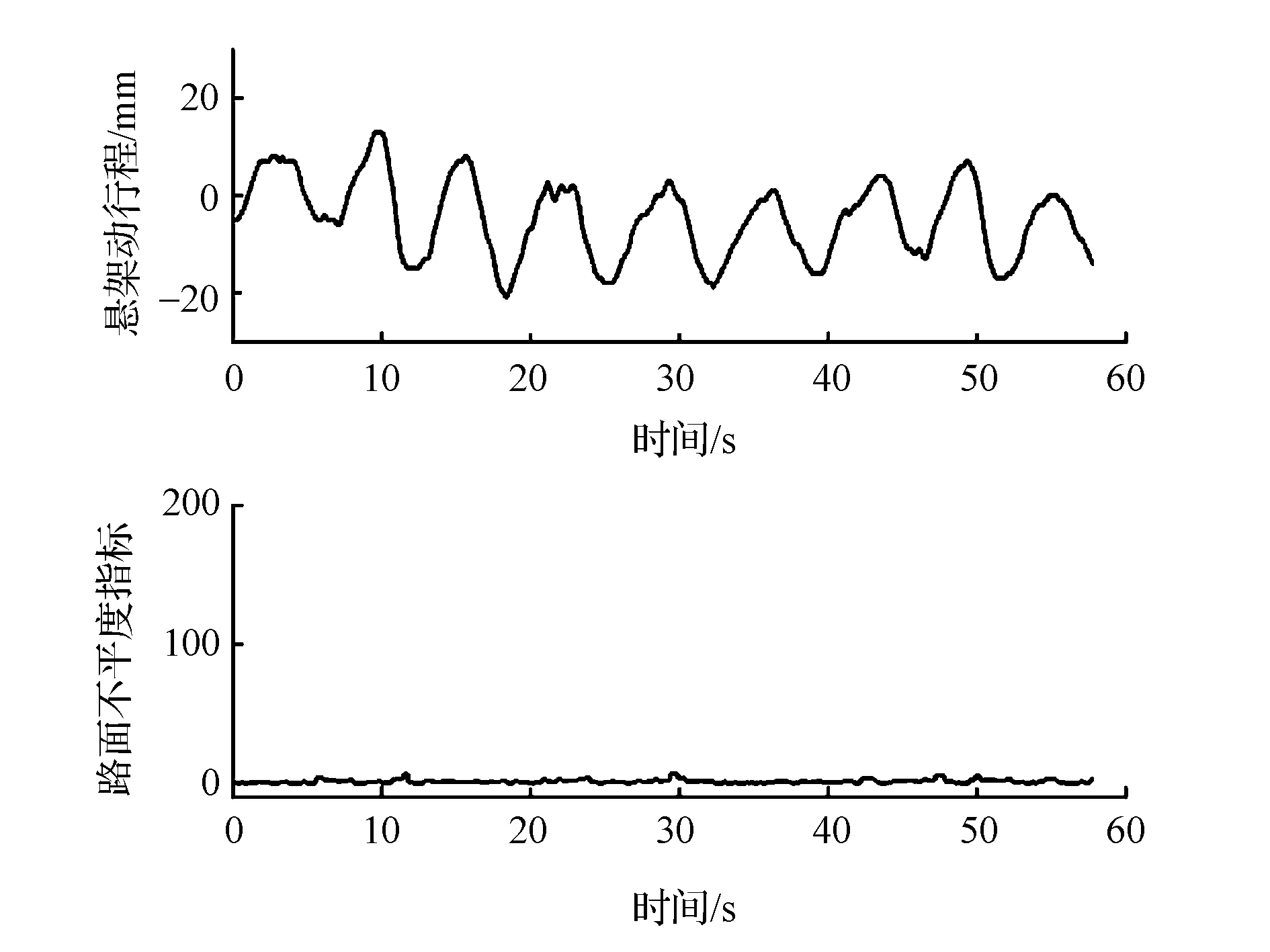
图10 水平良好路面蛇行不平度辨识结果
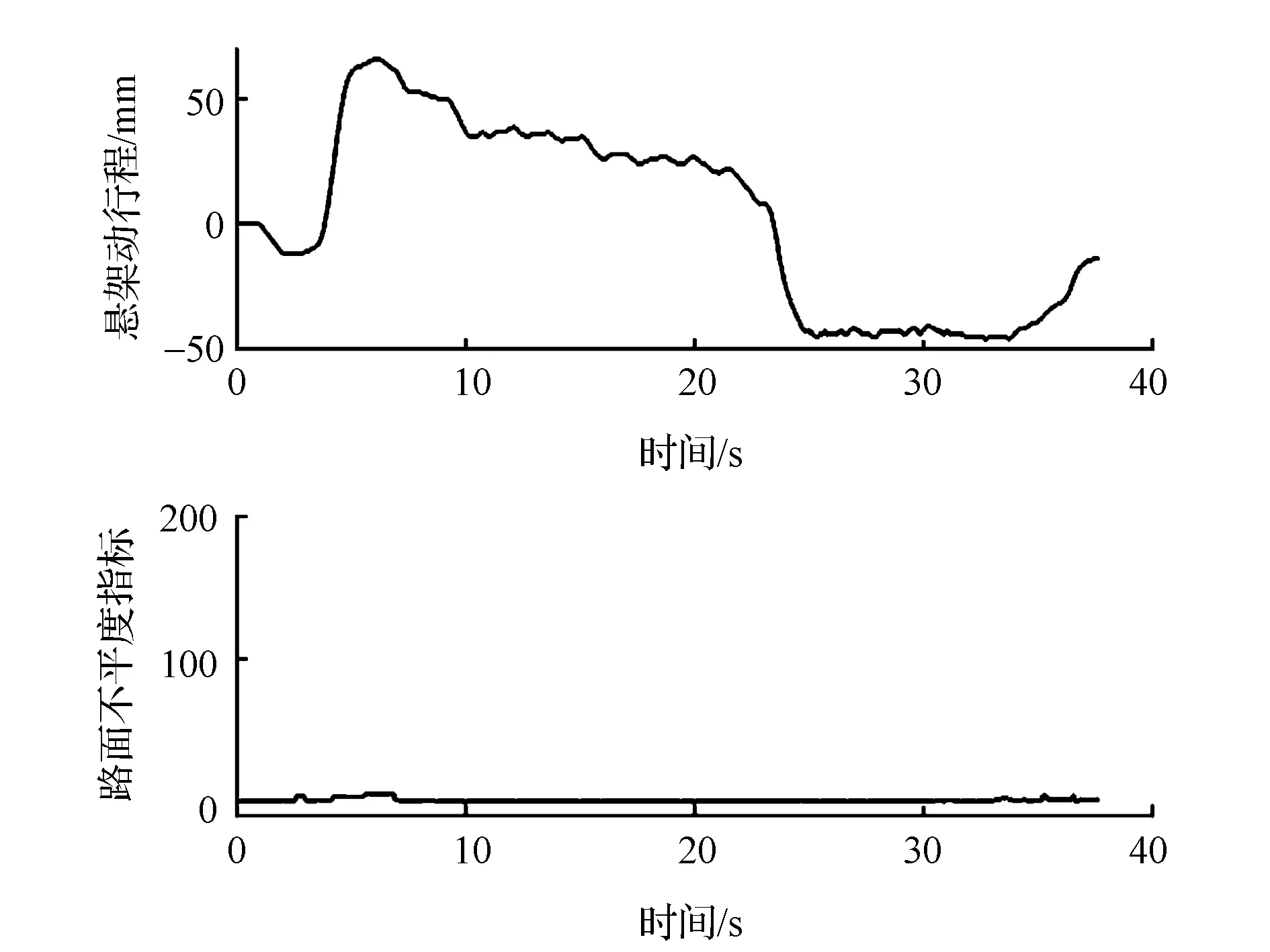
图11 水平良好加减速不平度辨识结果
5 结论
以某SUV为目标车型,提出了基于悬架动行程解耦的路面不平度识别算法,并进行了道路试验验证。结果表明:以车辆每行驶1m的距离时,悬架动行程曲线与横轴所围成的面积来表征路面不平度的指标,该指标可以有效反映路面不平特征;基于修正阻尼的1/2车辆振动模型的悬架动行程计算算法效果良好,据此可以实现悬架动行程的有效解耦;所设计的路面不平度识别算法可以有效识别不平路面,且水平良好路面上的急加速、急制动与急转向不会造成算法的误识别。
[1]BARHILLELA,LERNERR,LEVID,etal.Recentprogressinroadandlanedetection:asurvey[J].MachineVisionandApplications, 2012, 25 (3): 727-745.
[3] WARD C C, IAGNEMMA K. Speed-independent vibration-based terrain classification for passenger vehicles[J]. Vehicle System Dynamics, 2009, 47 (9): 1095-1113.
[4] CREMEAN L B, MURRAY R M. Model-based estimation of off-highway road Geometry using single-axis LADAR and inertial sensing[C]. ICRA 2006.
[5] 李忠国, 张为公, 刘庆华,等. 基于车轮垂直动载的路面不平度识别研究[J]. 仪器仪表学报, 2006(S3).
[6] 余志生. 汽车理论[M]. 第3版. 北京: 机械工业出版社, 2000.
[7] Thai Minh Do,Thong Chi Le. Performance analysis of FFT filter to measure displacement signal in road roughness profiler[J]. International Journal of Computer & Electrical Engineering, 2013, 5(4):356-361.
A Study on the Road Roughness Identification Algorithm for SUVs Based on Decoupling of Suspension Deflection
Zhang Jian, Liu Qiuzheng, Wang Kang, Liu Ye & Li Suwen
R&DCenterAutomotiveElectronicsDepartment,ChinaFAWCo.,Ltd.,Changchun130011
Based on the dynamic suspension deflection signals measured on the semi-active suspension of a SUV, the frequency characteristics of its dynamic suspension deflection are analyzed. An algorithm for suspension deflection decoupling is devised based on vehicle acceleration to eliminate the effects of suspension deflection variation caused by vehicle inertial force on the identification results of road surface irregularity. Then an algorithm is proposed which takes the integral of suspension dynamic deflection in a preset driving distance of vehicle as an indicator of road surface irregularity identification. Finally a real vehicle road test for verification is conducted with a result showing that the algorithm devised can effectively distinguish between well paved road and rough road, and brisk acceleration, hard braking and sharp turning of vehicle will not result in misidentification.
SUV; road roughness identification; suspension deflection decoupling; suspension model
原稿收到日期为2016年7月4日,修改稿收到日期为2016年8月8日。
