基于可拓理论的汽车主动悬架系统H∞控制与优化*

汪洪波,林 澍,孙晓文,杨柳青,陈无畏

(合肥工业大学机械与汽车工程学院，合肥 230009)

2016218

基于可拓理论的汽车主动悬架系统H∞控制与优化*

汪洪波,林 澍,孙晓文,杨柳青,陈无畏

(合肥工业大学机械与汽车工程学院，合肥 230009)

本文中在汽车主动悬架系统H∞控制的基础上，建立其H∞可拓控制器，并利用Matlab/Simulink软件对被动悬架和两种不同控制下的主动悬架系统进行对比仿真。结果表明，H∞可拓控制可提高H∞控制的鲁棒性，改善了汽车悬架控制性能和汽车乘坐舒适性。最后，通过实时动态调整可拓控制系数，进一步提高了主动悬架的控制性能。

主动悬架；H∞控制；可拓控制；参数摄动

前言

近年来 , 由蔡文先生建立和发展的崭新理论——物元分析，引起了学术界的兴趣和重视[1]。接着，文献[2]中在物元分析的研究中，提出了一种新型智能控制——可拓控制，它的基本思想是从信息转换角度去处理控制问题，即以控制输入信息的合格度(关联度)作为确定控制输出校正量的依据，从而使被控信息转换到合格范围内。之后，文献[3]中又在上述思想的启迪下，进行了进一步探索和研究，提出了一种可拓控制器的设计，探讨了特征模式划分和关联度计算等问题。

悬架系统作为汽车底盘的重要组成部分，将车身和轮胎联系在一起，直接影响到汽车的平顺性和操纵稳定性。相对于被动悬架，主动悬架可通过调整控制力来改变悬架的阻尼和刚度，进而改善汽车的操纵稳定性、舒适性和安全性。如何调整主动悬架的控制力一直是研究主动悬架的关键，即主动悬架的控制策略是对其研究的重中之重。文献[4]中研究了LQG作为悬架控制器的自适应控制，仿真结果表明该方法可以获得较好的控制性能，但在参数不确定和路面干扰的情况下，其系统存在一定的稳态误差。为此，如文献[5]中采用了H∞和鲁棒LQR控制器使系统的稳定性得到更进一步的提升。文献[6]中研究了一种鲁棒保性能的控制方法，将车身加速度作为H2的性能指标，而悬架动行程和轮胎动载荷作为H∞的性能指标，改善了汽车的舒适性。然而在主动悬架控制问题中，只考虑量值与量值之间的关系是远远不够的，众多相关联的微分方程下复杂的特征属性与转化关系无疑给描述主动悬架的控制特性带来了困难。可拓学的出现与发展为描述和研究智能控制提供了一种新的手段和方法。基于可拓理论的可拓控制，探讨了特征模式划分和关联度计算等实现问题，可有效地解决以上复杂的转化问题。此外，不再局限于传统的被动悬架上，刚度、阻尼等参数的优化设计，以平顺性、操纵稳定性和舒适性为优化目标，主动悬架的控制规则也逐步使用各种不同的优化方法，协调各冲突因素，使车辆系统的总体性能达到最佳[7]。

本文中考虑到主动悬架控制系统的鲁棒性要求，首先设计其H∞控制器；在此基础上，选取了相关性能指标的偏差及其微分，将特征状态所在的特征平面划分为经典域、可拓域和非域，对可拓域和非域的特征状态进行调整并设计对应的控制算法，建立H∞可拓控制器，这样不仅保证其控制系统的鲁棒性，还可对特征状态进一步调整，拓展控制器的设计以改善主动悬架系统的控制性能；然后对H∞控制和H∞可拓控制下主动悬架系统的性能指标进行对比仿真，结果证明H∞可拓控制的优越性。最后针对常见的悬架系统参数簧载质量与悬架刚度的变化，进行拟合与优化，对悬架可拓控制器重要的参数即可拓控制系数寻优求解，通过可拓控制器实时动态地调整参数，以进一步全面改善主动悬架的控制性能。

1 整车悬架系统建模与H∞控制

考虑到车身的垂向、侧倾、俯仰运动和车轮的垂向运动，建立7自由度整车模型，如图1所示。具体所建方程参见文献[8]，本节不再详述。

图1 7自由度整车悬架系统模型示意图

图中：Zb为车身位移；a，b为车身质心到前后轴的水平投影距离；l为1/2轮距；mb为簧载质量；mwi为非簧载质量；Csi为悬架阻尼系数；ksi为悬架刚度；Ip为车身俯仰转动惯量；Ir为车身侧倾转动惯量；kti为轮胎刚度；θ为车身俯仰角；φ为车身侧倾角；Zwi为第i个车轮垂直位移；Zgi为第i个车轮处的路面位移；fi为第i个悬架的控制力；Zbi为簧载质量的垂直位移。

H∞控制具有很好的鲁棒性，适用于有模型摄动的多输入多输出系统的控制。在汽车行驶中，悬架受到的干扰因素较多，例如，路面的无规律起伏所产生的干扰输入，乘员上下车引起簧载质量的变化和刮风下雨天气的影响等，其模型存在着参数不确定性，本节首先采用H∞控制器对主动悬架模型进行控制。H∞控制的目的是设计一控制器K(s)，使得闭环系统内部稳定，且‖Tzw(s)‖达到最小，其中Tzw(s)代表从干扰输入W到被控输出Z的闭环传递函数。为提高系统的鲁棒性并改善系统的评价指标，获得更好的控制效果，分别引入加权系数矩阵Sw，Sz和加权传递函数矩阵Wp，具体参数见文献[9]，构建主动悬架H∞加权控制系统框图，如图2所示。

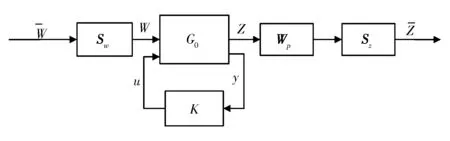
图2 H∞加权控制系统框图

利用Matlab软件中的LMI工具箱可求得H∞控制器，H∞控制可使悬架系统获得很好的鲁棒性能。

2 主动悬架H∞可拓控制器设计

机器在运转过程中,经常要产生形形色色的矛盾问题，能否在机器中装上能处理该领域矛盾问题的智能系统，并指挥机器把该矛盾问题转化为不矛盾问题,这是一项具有前瞻性的重要课题，其目的是创制高水平的智能系统[10]。当机器遇到不可处理的矛盾问题时，可拓控制的理论与方法[11-13]能给出有效的解决策略，智能地将矛盾问题转化为不矛盾问题。

汽车悬架本身是一个充满矛盾的汽车总成，因为它既要满足汽车操纵稳定性的要求，又要保证汽车的舒适性要求，而这两方面又相互矛盾。主动悬架的控制过程也存在许多矛盾问题，众多相关联的微分方程，复杂的特征属性与转化关系无疑给描述主动悬架的控制特性带来了困难。再结合悬架对智能特性的发展追求[14]，近年来，可拓控制在汽车悬架方面也已开始初步的应用[15]。

由第1节可知，H∞控制可使悬架系统获得很好的鲁棒性能。考虑到上述原因，及可拓控制本身具有的良好的控制品质和较好的自学习能力,在H∞控制的基础上，引入可拓控制。选择主动悬架的车身质心垂直加速度、俯仰角速度和侧倾角速度作为系统状态的特征量，并对这3个性能指标的值域进行划分，即包括原有的经典域、进行优化的可拓域和控制效果相对较差的非域。将H∞控制器在不同值域内进行拓展设计，在不同值域内设计对应的局部最优控制器，从而建立全域H∞可拓控制器，以进一步提升主动悬架系统控制性能。

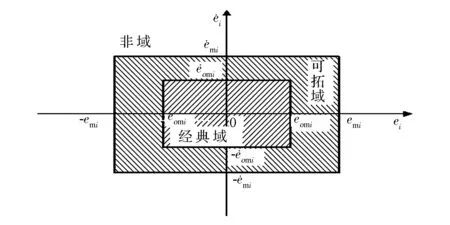
图3 关于特征状态的可拓集合

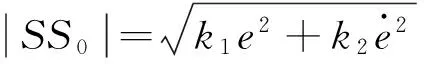
式中：Rgy为经典域(见图3)；k1和k2为加权系数。

根据特征平面某点位置计算关联函数值，根据关联函数值对应的不同值域范围，设计对应的控制算法，具体如图4所示。

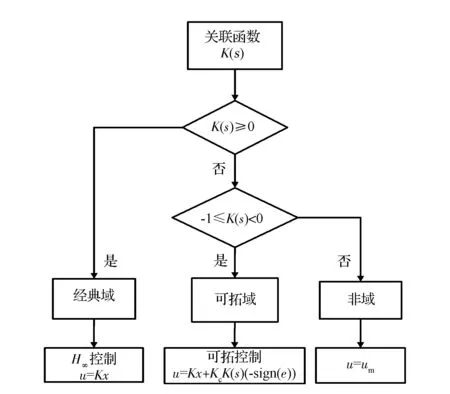
图4 不同值域内对应控制算法

其中，Kc为主动悬架在该模式下的控制系数，sign(e)为偏差符号函数。在经典域中，采用H∞控制方法；在可拓域中，构造控制算式u=Kx+KcK(s) (-sign(e))，实现H∞控制的拓展；在非域中，采用该状态下的最大输出值um为控制器输出，尽可能维持该范围内的控制性能，从而建立全域中的H∞可拓控制器。

3 仿真结果分析

仿真中为对比H∞控制和H∞可拓控制，首先对不同路面输入(白噪声和单位脉冲)下的主动悬架系统进行时域仿真，对其性能指标进行比较；然后分别对两种控制方法下的主动悬架进行汽车乘坐舒适性分析。仿真中使用的整车悬架参数如表1所示，可拓控制器参数如表2所示。

表1 部分整车参数

表2 可拓控制器参数

3.1 白噪声干扰输入下仿真结果分析

将白噪声作为路面干扰输入，对被动悬架和主动悬架系统的各项性能进行分析。图5为被动悬架、H∞控制和H∞可拓控制下主动悬架的车身质心加速度、俯仰角加速度、侧倾角加速度和右前悬架动挠度的时域响应曲线。

从图5中可以看出，H∞控制下主动悬架的时域响应曲线波动的范围明显小于被动悬架的响应曲线，H∞可拓控制的时域响应曲线的波动范围更小，进一步提高了主动悬架的性能。

另外，为更精确地分析被动悬架和主动悬架各项性能，表3给出了相关性能指标的峰值和均方根值，以进一步比较在白噪声干扰输入下H∞控制和H∞可拓控制的控制效果。

由表3可知，H∞可拓控制下的车身垂直加速度、俯仰角加速度、侧倾角加速度和右前悬架动挠度的峰值和均方根值都小于H∞控制下的数值，其峰值分别减小了38.1%，16.1%，10.9%和23.8%，均方根值分别减小了4.3%，14.3%，16.1%和27.3%。另外，H∞控制的主动悬架较被动悬架的各性能指标的峰值分别减小了3.5%，15.9%，38.4%和13.7%，而均方根值分别减小了16.1%，22.2%，35.7%和15.4%。

由此可见，当外界干扰为白噪声输入时，H∞可拓控制下的主动悬架性能指标最佳，H∞控制次之，被动悬架性能最差。

3.2 脉冲干扰输入下仿真结果分析

将单位脉冲信号作为主动悬架的外部干扰输入，对比不同控制方法下悬架系统的控制效果，如图6所示。

图6 脉冲输入下的时域响应

由图6可见，H∞控制下的主动悬架无论是响应峰值还是趋于稳态的时间，均要小于被动悬架；而H∞可拓控制下的车身质心垂直加速度、俯仰角加速度、侧倾角加速度和右前悬架动挠度响应皆能更快地趋于稳态，且动态响应的波动更小。

为进一步分析被动悬架和不同控制方法下的主动悬架受到冲击的响应情况，表4给出了各性能指标的峰值和到达稳态所需的调节时间。

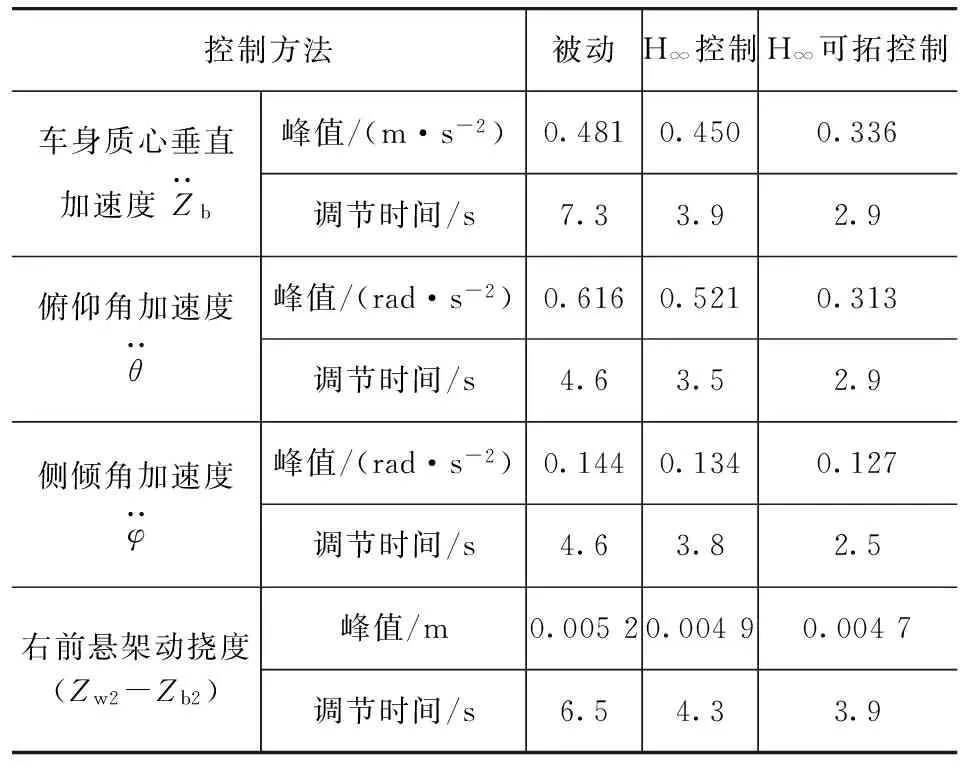
表4 单位脉冲输入下性能指标比较

由表4可知，在单位脉冲输入下，H∞可拓控制下的车身质心垂直加速度、俯仰角加速度、侧倾角加速度和右前悬架动挠度的峰值较H∞控制分别减小了25.3%，39.9%，5.2%和4.1%，调节时间分别缩短了25.6%，17.1%，34.2%和9.3%；而H∞控制控制下的各性能指标的峰值较被动悬架分别减小了6.4%，15.4%，6.9%和5.8%，调节时间分别缩短了46.6%，23.9%，17.4%和33.8%。

因此，当主动悬架受到外界冲击输入时，H∞可拓控制有着最好的控制效果，可比H∞控制更进一步提高主动悬架的整体性能，改善汽车乘坐舒适性。

3.3 汽车乘坐舒适性分析

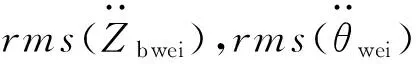
取kz=1，kθ=0.4，kφ=0.63。结果如表5所示。

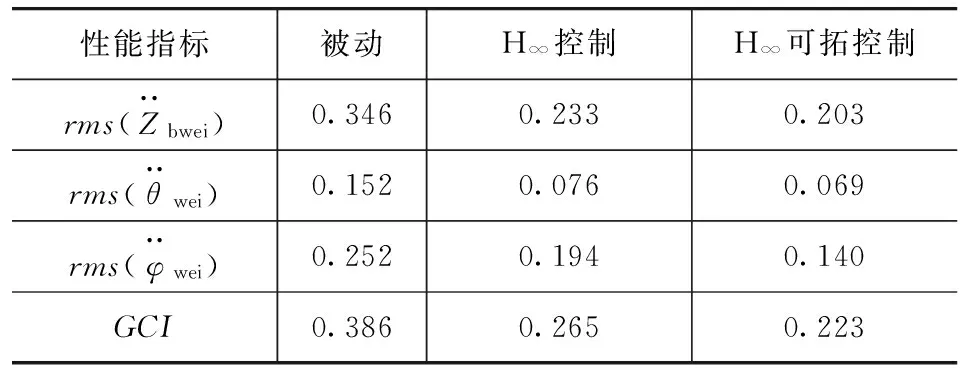
表5 汽车乘坐舒适性比较

由表5可知，采用H∞控制，其加权质心垂直加速度、加权俯仰角加速度和加权侧倾角加速度的均方根值较被动悬架分别减小了32.7%，50.0%和23.0%，GCI减小了31.3%；而H∞可拓控制下加权质心垂直加速度、加权俯仰角加速度和加权侧倾角加速度的均方根值较H∞控制分别减小了12.9%，9.2%和27.8%，GCI减小了15.8%。故H∞可拓控制对应的汽车乘坐舒适性要优于H∞控制。

4 可拓控制系数优化与分析

由第3节内容可知，当悬架系统参数取标准参数时，所设计的H∞可拓控制可有效提高主动悬架的控制性能。现实中，悬架系统参数往往会发生不同程度的摄动，如簧载质量与悬架刚度的变化，采用固定不变的控制系统参数可能难以保证主动悬架始终维持最优的性能。本节考虑簧载质量与悬架刚度在一定范围内变化，定义优化评价指标J，以其最小作为优化目标，运用多项式拟合与Matlab优化工具箱，对悬架可拓控制器重要的参数即可拓控制系数Kc寻优求解，通过实时动态地调整可拓控制系数Kc，获得针对悬架系统参数变化时对应的最优可拓控制器参数，进一步满足主动悬架对系统鲁棒性的要求。

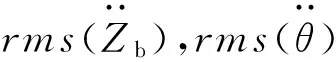
定义优化评价指标J:

取α=5，β=2，γ=3为加权系数。直接建立Kc与J之间的函数关系J=f(Kc)，以最小化评价指标J作为优化目标，对一定范围的Kc寻优求解。

由于在H∞可拓控制下的仿真过程中，评价指标J与可拓控制系数Kc无法得到直接的函数关系，所以，本文中在文献[8]原悬架系统数学模型的基础上，增加H∞可拓控制器，并采用拟合函数的方法获得目标函数。选取一车辆标称簧载质量1 500kg，悬架刚度190 000N/m，每隔2%对簧载质量和悬架刚度选取一个参数摄动点，同时令Kc的变化范围处于一个相对合理的区间(本文中取[0,5])，并每隔一定的步长(本文中取0.2)运行一次仿真，将不同的Kc与其仿真结果J一一对应。对这些点进行多项式拟合，不断调试拟合阶数直至R方值大于某个临界值(本文中取0.998)时，确定合适的拟合阶数，并在此拟合阶数下得到拟合函数，即为目标函数J=f(Kc)。

在Matlab软件中编程实现上述拟合过程，利用Matlab优化工具箱的FMINBND函数对J进行有界单变量优化，获得局域内的最优Kc值，并得到其对应的最优J值。表6给出簧载质量变化率10%，前左悬架刚度变化率-10%～10%的统计数据。由此算例可知，当簧载质量和悬架刚度变化时，最优的Kc值也在随之变化，并不存在唯一最优的可拓控制系数Kc。所以，为得到最优的评价指标J，应对Kc进行适应性地动态调整。

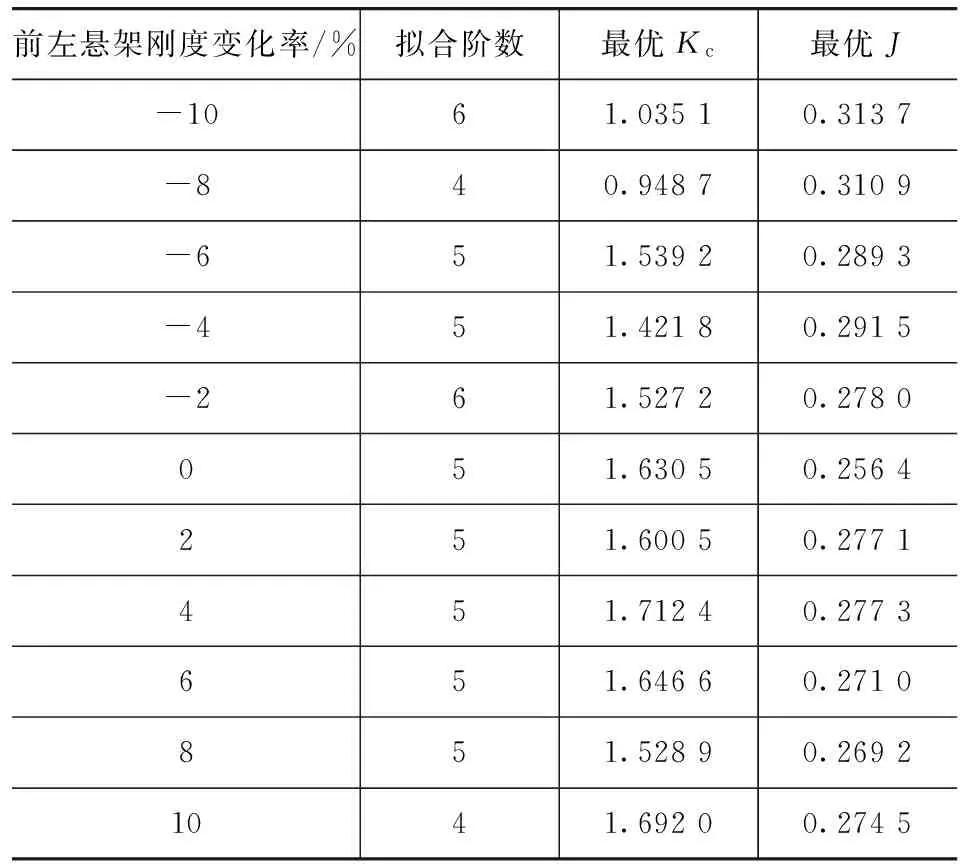
表6 悬架参数变化时对应的拟合与优化结果

为分析可拓控制系数Kc与簧载质量变化率、悬架刚度变化率之间的关系，选取悬架刚度和簧载质量分别单独变化的情况进行分析。表7给出前左悬架刚度为190 000N/m时，簧载质量mb变化率从-10%到10%变化时，可拓控制系数Kc与优化指标J对应的优化值。图7给出了其两者变化的对应曲线图。

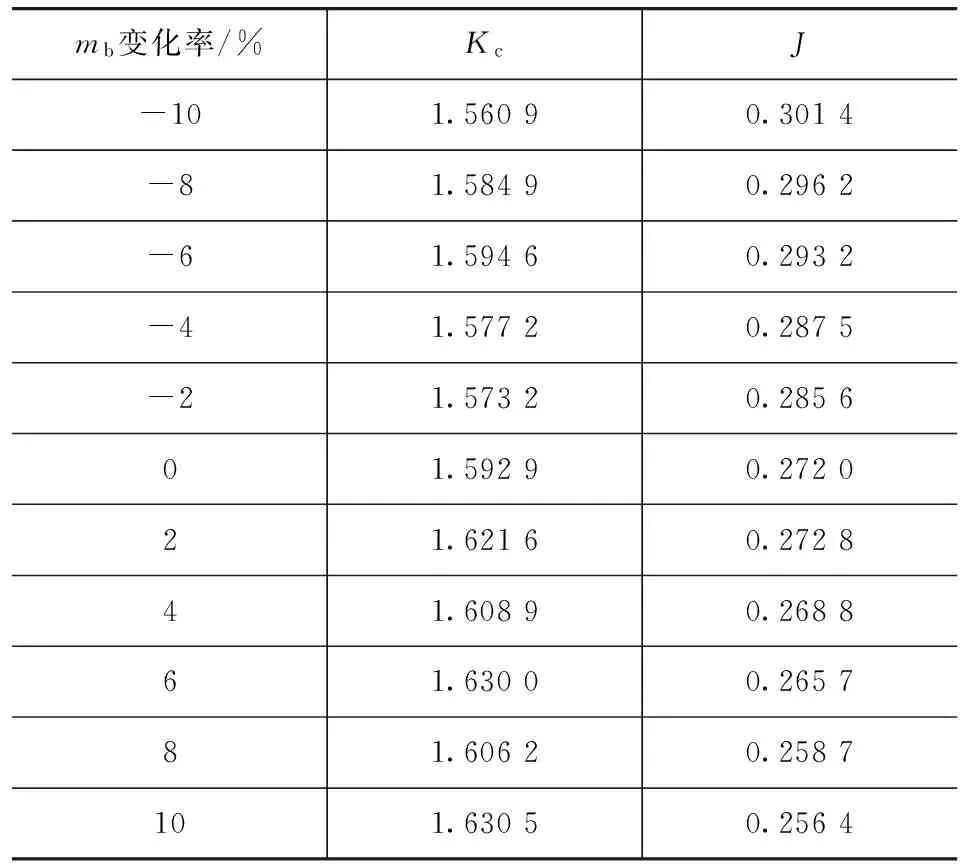
表7 mb变化时对应的优化结果

图7 可拓控制系数与簧载质量变化率的关系曲线图

表8为簧载质量1 500kg时，前左悬架刚度变化率从-10%到10%变化时，可拓控制系数Kc与优化指标J对应的优化结果。图8为其两者变化的对应曲线图。

表8 ks1变化时对应的优化结果

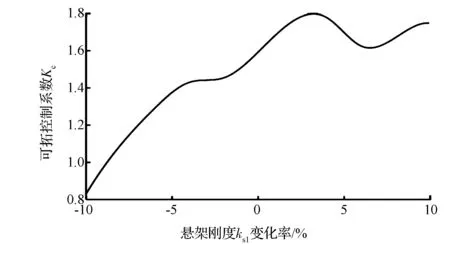
图8 可拓控制系数与悬架刚度变化率的关系曲线图

由图7、图8、表7和表8可以看出，簧载质量与悬架刚度的变化对最优可拓控制系数Kc选取有着很大影响。为提高悬架系统的鲁棒性并改善悬架系统的控制性能，需要针对簧载质量与悬架刚度的变化，对Kc做动态地优化调整。

为体现Kc寻优取值的优越性，下面针对Kc的3种不同取值下的评价指标J进行分析，其中当Kc=0时，控制器中不施加可拓控制，仅处于H∞控制下；当Kc为某一固定值时，主动悬架处于H∞可拓控制下，这里取Kc=1进行分析；当Kc取优化值时，Kc处于一个动态调整的状态，能针对外界参数做出适应性的改变，保持悬架系统最优控制性能和良好的鲁棒性。图9和图10分别为簧载质量mb和前左悬架刚度ks1变化时，评价指标的变化情况。

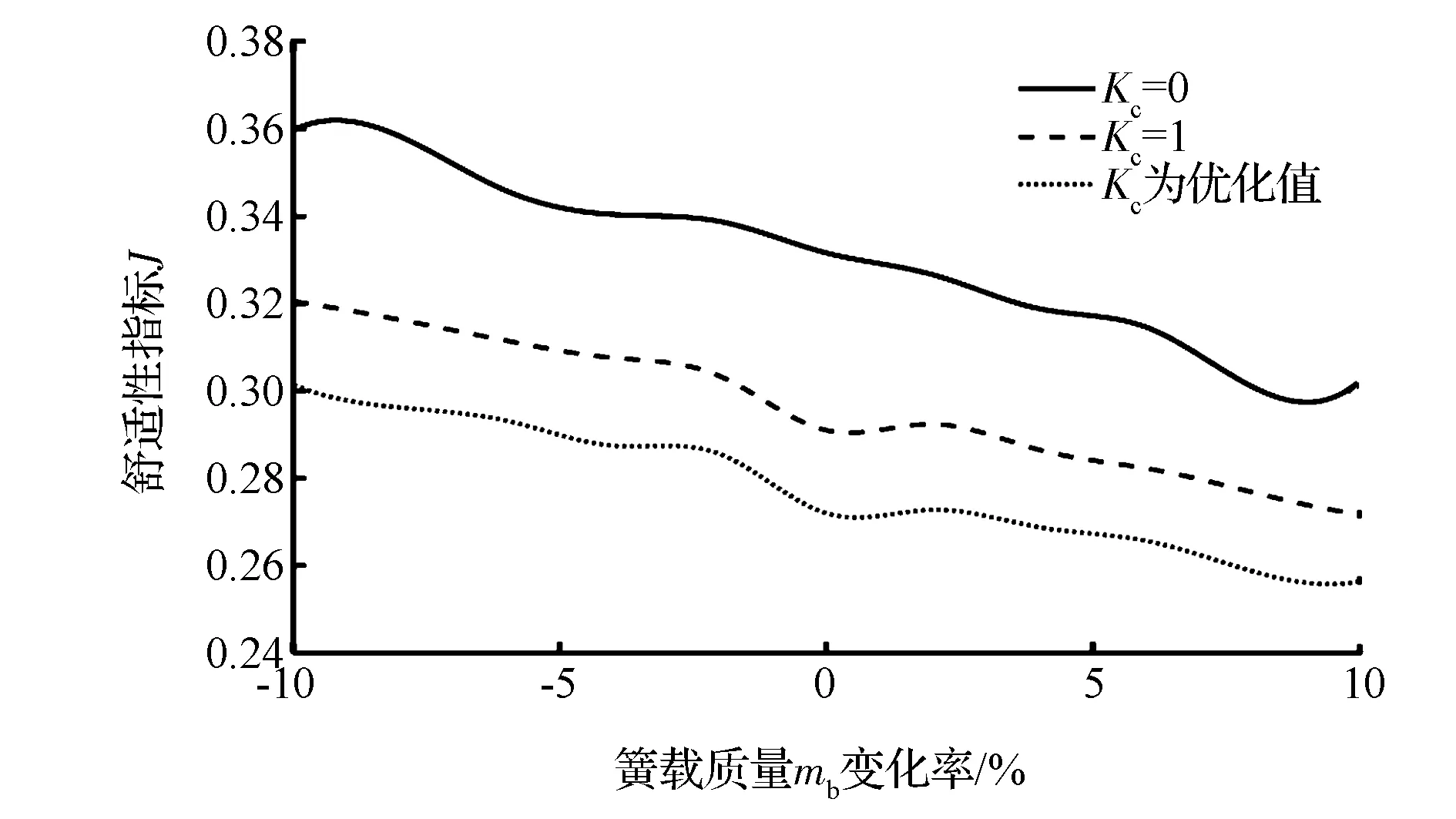
图9 簧载质量变化时，不同Kc下J的比较图

图10 前左悬架刚度变化时，不同Kc下J的比较图

根据J的值越小汽车乘坐舒适性越好，可得出以下结论：当前左悬架刚度维持不变时，改变簧载质量，Kc为优化值对应的J值整体均小于Kc=1的情况，若发生相同的参数摄动，Kc为优化值的J相对于Kc=1时，最大减小率达6.70%，最小减小率亦有5.67%；而Kc=1的J值整体也小于Kc=0的情况，若发生相同的参数摄动，Kc=1的J相对于Kc=0时，最大减小率为12.24%，最小减少率为8.01%。可见处于优化后的H∞可拓控制下的主动悬架性能指标最佳；Kc取固定值时H∞可拓控制对应的悬架性能次之；Kc=0时H∞控制对应的悬架性能相对最差。当簧载质量维持不变时，前左悬架刚度改变后，Kc为优化值的J值整体上不劣于Kc=1的情况，若发生相同的参数摄动，Kc为优化值的J相对于Kc=1时，最大减小率为7.12%，最小减小率为0.21%；而Kc=1的J值整体也小于Kc=0的情况，Kc=1的J相对于Kc=0时，最大减小率为12.24%，最小减少率为2.35%。可见处于优化后Kc的H∞可拓控制下的悬架性能最佳，H∞可拓控制次之，H∞控制相对最差。

在上述基础上，图11给出了评价指标J与同时变化的前左悬架刚度和簧载质量的三维关系曲面图。

由图11可见：当悬架处于H∞控制下时，J的最优值为0.300 3、最劣值为0.419 5；当悬架处于H∞可拓控制下时，J的最优值为0.269 3、最劣值为0.404 2，采用可拓控制后J分别减小10.32%和3.66%；当悬架处于优化后的H∞可拓控制下时，J的最优值为0.256 4、最劣值为0.397 2，J分别进一步减小4.79%和1.72%。从图11亦可见：H∞控制下评价指标随簧载质量和前左悬架刚度变化的波动较大，跳变点较多；而H∞可拓控制和优化后的H∞可拓控制明显波动较小、跳变点少，在维持良好的汽车舒适性方面，具有更好的鲁棒性。进而，对H∞可拓控制(对应优化指标Jh)与优化后的H∞可拓控制(对应优化指标J优化)进一步比较，构造相对变化率指标ΔJ=(J优化-Jh)/Jh。图12为ΔJ与同时变化的悬架刚度和簧载质量的三维关系曲面图，其中ΔJ值最大为-0.14%，最小达-15.27%，整体均小于0，可见优化后的H∞可拓控制对应的悬架控制性能优于H∞可拓控制。

因此，在悬架系统参数发生变化时，通过动态调整及优化可拓控制系数Kc值，可使整车主动悬架系统获得最优的控制性能，汽车悬架控制系统鲁棒性能最佳。

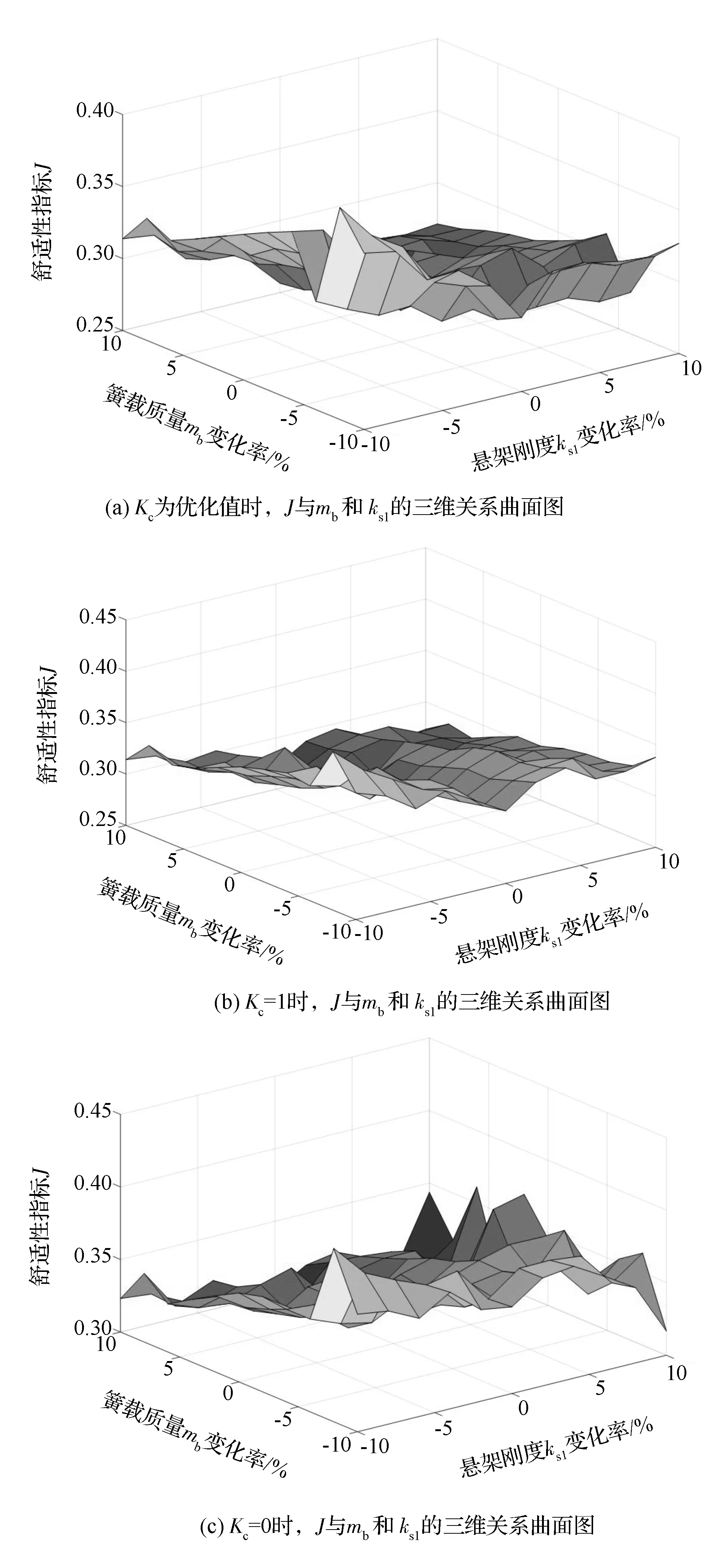
图11 J与mb和Ks1的三维关系图

图12 ΔJ与悬架刚度和簧载质量变化图

5 结论

针对主动悬架系统H∞控制器，基于可拓理论，建立了H∞可拓控制器。对被动悬架系统、H∞控制器和H∞可拓控制器构成的主动悬架系统进行仿真比较与分析，并对处于H∞可拓控制器下的悬架可拓控制Kc进行优化。结果表明，H∞可拓控制比H∞控制具有更好的抗干扰和模型参数摄动的能力，能进一步提高悬架性能，改善汽车乘坐舒适性，通过实时动态地调整可拓控制系数，还能更进一步提高主动悬架控制性能，为设计、优化主动悬架系统提供了一种新途径。

[1] 蔡文. 物元分析[M]. 广州： 广东高等教育出版社, 1987.

[2] LI Jian, WANG Shienyn. Primary research on extension control[J]. Pro of International Conference on Information and Systems, AMSE 1991, Hangzhou, China, 1991, 1:392-395.

[3] 李健, 王行遇. 一类可拓控制器的设计[C]. 全国智能控制和自适应控制理论与应用研讨会论文集, 西安, 1993, 10.

[4] ABDEL HADY M B A, CROLLA D A. Active suspension control algorithm for a four wheel vehicle model[J].International Journal of Vehicle Design, 1992,13(2):144-158.

[5] MICHELBERGER P, PALKOVICS L, BOKOR J. Robust design of active suspension system[J]. International Journal of Vehicle Design, 1993, 14: 145-165.

[6] 龙垚坤，文桂林，陈哲吾. 汽车主动悬架鲁棒保性能控制仿真研究[J]. 汽车工程, 2014, 36(2):216-221.

[7] 孙鹏远.基于LIM的主动悬架多目标控制研究[D].长春:吉林大学, 2004.

[8] 方敏，汪洪波，刘跃, 等. 基于功能分配的汽车主动悬架控制的研究[J]. 汽车工程, 2015, 37(2): 200-206.

[9] 汪洪波. 汽车主动悬架系统控制器降阶和集成控制研究[D]. 合肥：合肥工业大学, 2006.

[10] 蔡文, 石勇. 可拓学的科学意义与未来发展[J]. 哈尔滨工业大学学报, 2006, 38(7):1079-1086.

[11] 王行愚, 李健. 论可拓控制[J]. 控制理论与应用, 1994, 11(1): 125-128.

[12] 潘东, 金以慧. 可拓控制的探索与研究[J]. 控制理论与应用, 1996,13(3) :305-311.

[13] 何斌, 朱学锋. 可拓自适应混杂控制研究[J]. 控制理论与应用,2005, 22(2):165-170.

[14] LIN J, LIAN R J. Intelligent control of active suspension systems[J]. Industrial Electronics, 2011, 58(2): 618-628.

[15] 陈无畏，汪洪波. 基于功能分配的汽车悬架/转向系统可拓控制及稳定性分析[J]. 机械工程学报, 2013, 49(24):67-75.

[16] 王其东，姜武华，陈无畏，等. 主动悬架和电动助力转向系统机械与控制参数集成优化[J]. 机械工程学报, 2008, 44(8):67-72.

H∞Control and Optimization for Vehicle Active Suspension System Based on Extension Theory

Wang Hongbo, Lin Shu, Sun Xiaowen, Yang Liuqing & Chen Wuwei

SchoolofMechanicalandAutomobileEngineering，HefeiUniversityofTechnology，Hefei230009

On the basis of vehicle active suspension system with H∞control, a H∞extensible controller is constructed and a comparative simulation is conducted on passive suspension and active suspensions with H∞controller and H∞extensible controller by using Matlab/Simulink. The results show that H∞extensible control can enhance the robustness of H∞control, and so improve the control performance of suspension and the ride comfort of vehicle. Finally by dynamically adjusting extensible control coefficient in real time, the control performance of active suspension is further improved.

active suspension; H∞control; extensible control; parameter pertubation

*国家自然科学基金(51305118)、中央高校基本科研业务费专项(JZ2014HGBZ0374)和江苏省道路载运工具新技术应用重点实验室开放基金(BM20082061504)资助。

原稿收到日期为2016年3月22日。