典型汽车碰撞模型病态问题的成因分析与处理*

张 健,张 鑫,梁 超,李 江

(1.北华大学汽车与建筑工程学院,吉林 132013； 2.人民交通出版社股份有限公司,北京 100011；3.吉林大学交通学院,长春 130022)

2016204

典型汽车碰撞模型病态问题的成因分析与处理*

张 健1,张 鑫2,梁 超1,李 江3

(1.北华大学汽车与建筑工程学院,吉林 132013； 2.人民交通出版社股份有限公司,北京 100011；3.吉林大学交通学院,长春 130022)

为解决典型汽车碰撞模型病态问题，根据其几何特征，应用线性空间与内积空间理论计算了模型中任意两个方程之间的夹角。结果表明，病态问题的成因在于模型中某些方程之间存在很强的线性相关性。通过对这些方程进行数学变换，在病态范围内建立了改进模型。应用摄动理论，提出了对改进模型可靠性的检验方法。实例检验结果表明，在病态范围内当模型系数存在1%误差时改进模型能将碰撞前车速误差控制在合理的范围内，说明在病态范围内建立改进模型能解决模型病态问题。

汽车碰撞模型；病态问题；误差；摄动理论

前言

以动量守恒定律和弹性变形为力学基础建立的典型汽车碰撞模型(以下简称模型)广泛用于计算碰撞前车速和事故原因分析[1-3]。模型为A0v0=Av形式，其中：A0和A为碰撞前和碰撞后车速向量系数矩阵；v0和v为碰撞前和碰撞后车速向量。A0和A中的系数包括：相互碰撞的两车质量(m1，m2)和绕车辆质心的转动惯量(以下简称转动惯量)、车身碰撞中心坐标和弹性恢复系数[4]。通过求解v0=inv(A0)·Av，能够快速计算碰撞前车速。但是，应用中发现当两车的质量比m2/m1处在m2/m1≈1,m2/m1>>1和m2/m1<<1范围时，如果A0中的系数存在微小的误差将导致模型计算的碰撞前车速产生较大的误差，模型出现病态问题。目前，国内主要通过现场勘查、事故车损坏状况评估和应用经验公式估算A0中的系数。由于主客观因素的影响，所确定的系数难免存在误差[5-6]。国外主要应用基于车对车碰撞试验开发的事故分析软件和数据库，采用正向模拟的方法计算碰撞前车速[7-8]，对此类问题涉及甚少。为了准确分析汽车碰撞事故的原因，扩展模型的应用范围，对于难以解决的模型病态问题，建立一种有效的处理方法尤为必要。为此，应用线性空间与内积空间理论分析了模型病态问题的形成原因；应用数学变换在病态范围内建立了改进模型，实现了对模型病态问题的有效处理。

1 模型

基于动量守恒定律和弹性变形条件，文献[4]中建立了由6个方程组成的模型，表示为

A01v01=A1v1

(1)

式中：A01和A1为碰撞前和碰撞后车速向量的系数矩阵；v01和v1为碰撞前和碰撞后车速向量。

v01=(v10n,v10τ,v20n,v20τ,ω10,ω20)T

v1=(v1n,v1τ,v2n,v2τ,ω1,ω2)T

式中：vi0n和vi0τ为碰撞前车速的法向和切向分量；i=1,2,本文中表示车辆1和车辆2；ωi0为碰撞前车辆绕其质心的横摆角速度(以下简称角速度)；vin和viτ为碰撞后车速的法向和切向分量；ωi为碰撞后车辆角速度。

(2)

式中:mi为车辆质量；xiτ和xin为车身碰撞中心的切向和法向坐标(简称切向和法向坐标)；Ji为转动惯量；μ和k为车身碰撞中心的切向碰撞冲量与法向碰撞冲量之比和弹性恢复系数；将A01中第6行元素依次用1，0，-1，0，-x1τ和x2τ替代后得到A1。模型的病态范围为m2/m1≈1,m2/m1>>1和m2/m1<<1。

2 病态问题的成因

根据线性空间与内积空间理论[9]，通过计算模型中两个方程之间的夹角来判断它们之间是否存在线性相关性。

θξη=arccos[|(Eξ,Eη)|/(‖Eξ‖·‖Eη‖)]

(3)

式中：θξη为两个方程之间的夹角；下标ξ和η代表方程ξ和方程η；|(Eξ,Eη)|为方程ξ和方程η的内积绝对值；‖Eξ‖和‖Eη‖为方程ξ和方程η的范数。θξη只取决于A0中的系数。

为研究模型病态问题的形成原因，选择质量比与病态范围相对应的4种代表车辆来模拟车辆碰撞。假设车辆1为被撞车辆，4种碰撞形式见表1。

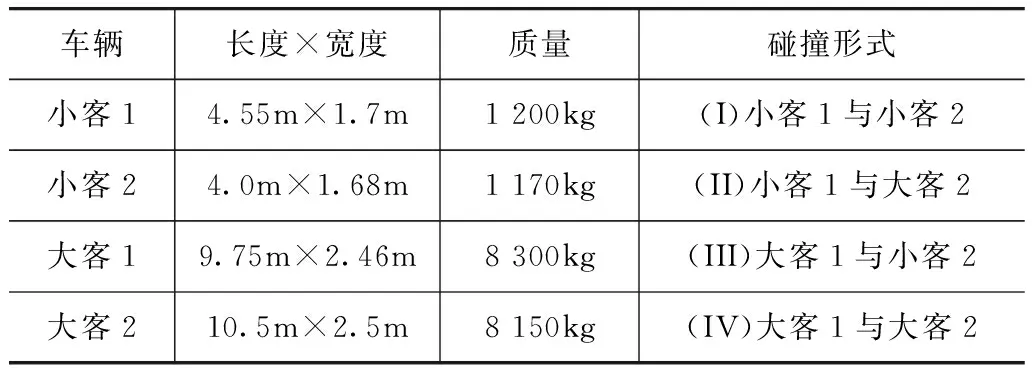
表1 车辆主要参数

代表车辆的Ji按文献[10]计算，取k=0.3，μ采用预估方法取值(见文献[11])。将4种碰撞形式的系数代入式(2)中，应用式(3)计算模型中两个方程之间的夹角(表2)。

由表2可知：(1)在4种碰撞形式中，θ15和θ25均小于50°，因此，模型中第1个方程与第5个方程和第2个方程与第5个方程之间存在非常严重的线性相关性，这是模型病态问题形成的主要原因；(2)在2种碰撞形式中，θ36和θ46均小于50°，因此，模型中第3个方程与第6个方程和第4个方程与第6个方程之间存在严重的线性相关性，这是模型病态问题形成的次要原因；(3)在1种碰撞形式中，θ13,θ23,θ14和θ24均小于50°，因此，模型中第1个方程与第3个方程之间，第2个方程与第3个方程之间，第1个方程与第4个方程之间和第2个方程与第4个方程之间存在线性相关性，这是模型病态问题形成的一般原因。

3 模型的重建

根据模型病态问题的成因，在病态范围内对存在线性相关性的方程进行重建，建立改进模型。

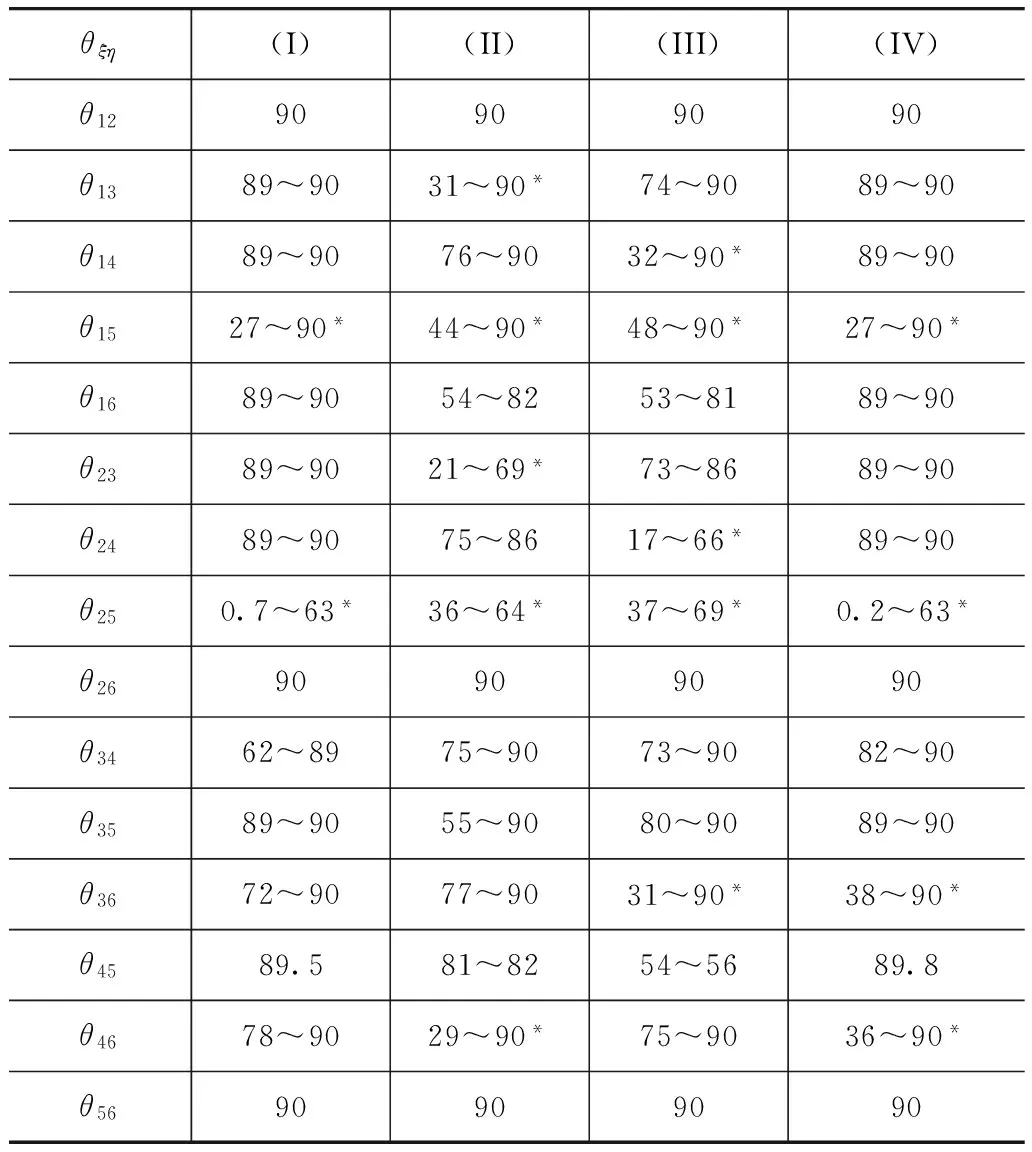
表2 4种碰撞形式的θξη (°)

注：*表示两方程之间存在线性相关性。

对文献[4]中μ的定义式进行数学变换，重建式(4)；应用动量定理，得到式(5)和式(6)。

μv10n-v10τ-μv20n+v20τ=μv1n-v1τ-μv2n+v2τ

(4)

ω10=ω1+(x1τ-μx1n)[m1(v1n-v10n)-

m2(v2n-v20n)]/(2J1)

(5)

ω20=ω2-(x2τ-μx2n)[m1(v1n-v10n)-

m2(v2n-v20n)]/(2J2)

(6)

用式(5)和式(6)替代模型中第6个方程中的ω10和ω20，重建式(7)。

b61v10n+b63v20n=c61v1n+c63v2n+c65ω1+c66ω2

(7)

其中：

b61=-k{1+0.5m1[(x1nτ/J1)+(x2nτ/J2)]}

b63=k{1+0.5m2[(x1nτ/J1)+(x2nτ/J2)]}

c61=1-0.5km1[(x1nτ/J1)+(x2nτ/J2)]

c63=-1+0.5km2[(x1nτ/J1)+(x2nτ/J2)]

c65=-(1+k)x1τ；c66=(1+k)x2τ

x1nτ=x1τ2-μx1τx1n；x2nτ=x2τ2-μx2τx2n

用式(4)和式(7)替代模型中第5个方程和第6个方程，得到第一改进模型为

A02v02=A2v2

(8)

式中：A02和A2为碰撞前和碰撞后车速向量的系数矩阵；v02和v2为碰撞前和碰撞后车速向量。

其中：

v02=(v10n,v10τ,v20n,v20τ,ω10,ω20)T

v2=(v1n,v1τ,v2n,v2τ,ω1,ω2)T

(9)

将A02中第6行元素依次用式(7)中c61，0，c63，0，c65和c66替代后得到A2。

第一改进模型的适用范围为m2/m1≈1。

应用动量定理，重建式(10)和式(11)。

m1(x1τv10n-x1nv10τ)+J1ω10=m1(x1τv1n-x1nv1τ)+J1ω1

(10)

m2(x2τv20n-x2nv20τ)+J2ω20=m2(x2τv2n-x2nv2τ)+J2ω2

(11)

对文献[4]中μ的定义式进行数学变换，重建式(12)；将模型中第3个方程和第4个方程相加，得到式(13)；对模型中第1个方程进行数学变换，得到式(14)。

μv10n-v10τ=μv1n-v1τ

(12)

ω20=ω2+[J1(ω1-ω10)/J2]-m2(v2n-v20n)·

[(x1τ-x2τ)-μ(x1n-x2n)]/J2

(13)

v20n=[m1(v1n-v10n)/m2]+v2n

(14)

用式(13)和式(14)替代模型中第6个方程中的ω20和v20n，重建式(15)。

b61v10n+b65ω10=c61v1n+c63v2n+c65ω1+c66ω2

(15)

其中：

b61=-k[1+(m1/m2)-(m1xnτ/J2)]

b65=k[x1τ+x2τ(J1/J2)]

c61=1-k[(m1/m2)-(m1xnτ/J2)]

c63=-(1+k)；c65=-x1τ+kx2τ(J1/J2)

c66=(1+k)x2τ；xnτ=x2τ[(x1τ-x2τ)-μ(x1n-x2n)]

用式(10)～式(12)和式(15)替代模型中第3个方程～第5个方程和第6个方程，得到第二改进模型，表示为

A03v03=A3v3

(16)

式中：A03和A3为碰撞前和碰撞后车速向量的系数矩阵；v03和v3为碰撞前和碰撞后车速向量。

其中：

v03=(v10n,v10τ,v20n,v20τ,ω10,ω20)T

v3=(v1n,v1τ,v2n,v2τ,ω1,ω2)T

(17)

将A03中第6行元素依次用式(15)中c61，0，c63，0，c65和c66替代后得到A3。

第二改进模型的适用范围为m2/m1>>1。

对文献[4]中μ的定义式进行数学变换，重建式(18)；应用动量定理，得到式(19)；对模型中第1个方程数学变换，得到式(20)。

μv20n-v20τ=μv2n-v2τ

(18)

ω10=ω1+m1(x1τ-μx1n)(v1n-v10n)/J1

(19)

v10n=v1n+[m2(v2n-v20n)/m1]

(20)

用式(19)和式(20)替代模型中第6个方程中的ω10和v10n，重建式(21)。

b63v20n+b66ω20=c61v1n+c63v2n+c65ω1+c66ω2

(21)

其中：

b63=k[1+(m2/m1)+(m2x1nτ/J1)]；b66=-kx2τ

c61=1+k；c63=-1+k[(m2/m1)+(m2x1nτ/J1)]

c65=-(1+k)x1τ；c66=x2τ；x1nτ=x1τ2-μx1τx1n

用式(18)和式(21)替代第二个改进模型中第5个方程和第6个方程，得到第三改进模型，表示为

A04v04=A4v4

(22)

式中：A04和A4为碰撞前和碰撞后车速向量的系数矩阵；v04和v4为碰撞前和碰撞后车速向量。

其中：

v04=(v10n,v10τ,v20n,v20τ,ω10,ω20)T

v4=(v1n,v1τ,v2n,v2τ,ω1,ω2)T

(23)

将A04中第6行元素依次用式(21)中c61，0，c63，0，c65和c66替代后得到A4。

第三改进模型的适用范围为m2/m1<<1。

4 改进模型的可靠性

根据摄动理论[9]，建立此类模型A0jv0j=Ajvj的可靠性算式，表示为

‖δv0j‖/‖v0j‖≤Cond(0j)[(‖δ0j‖/‖0j‖)+

(‖δjvj‖/‖jvj‖)]/(1-‖0j-1‖·‖δ0j‖)

(24)

式中：j=1,2,3,4代表4个模型；v0j为碰撞前车速向量，‖δv0j‖/‖v0j‖为碰撞前车速误差；0j=D0jA0j，A0j为碰撞前车速向量的系数矩阵；j=D0jAj，Aj为碰撞后车速向量的系数矩阵；D0j=diag(1/d1,1/d2,…,1/d6)为平衡矩阵，d1～d6为A0j中每行元素绝对值的最大值；Cond(0j)为D0jA0j条件数；符号‖‖表示范数；δ0j=D0jδA0j，δA0j为A0j的扰动矩阵；δj=D0jδAj；δAj为Aj的扰动矩阵；‖δ0j‖/‖0j‖和‖δjvj‖/‖jvj‖为A0j和Ajvj的误差；vj为碰撞后车速向量。

根据运动学公式，计算碰撞后车速为

vin=(2gsifi)1/2cosθi

(25)

viτ=(2gsifi)1/2sinθi

(26)

ωi=π(αi-αi0)(2gfi/si)1/2/180

(27)

式中：g为重力加速度；si为车辆滑行距离；fi为路面摩擦因数；θi为车辆滑行方位角；αi为停车方位角；αi0为碰撞前车速方位角。

案例介绍[12]：某城市道路交叉口处，由西向东行驶的面包车(车辆1)右侧面受到左转的轿车(车辆2)右前部的猛烈撞击，两车严重损坏。现场勘查数据见表3。

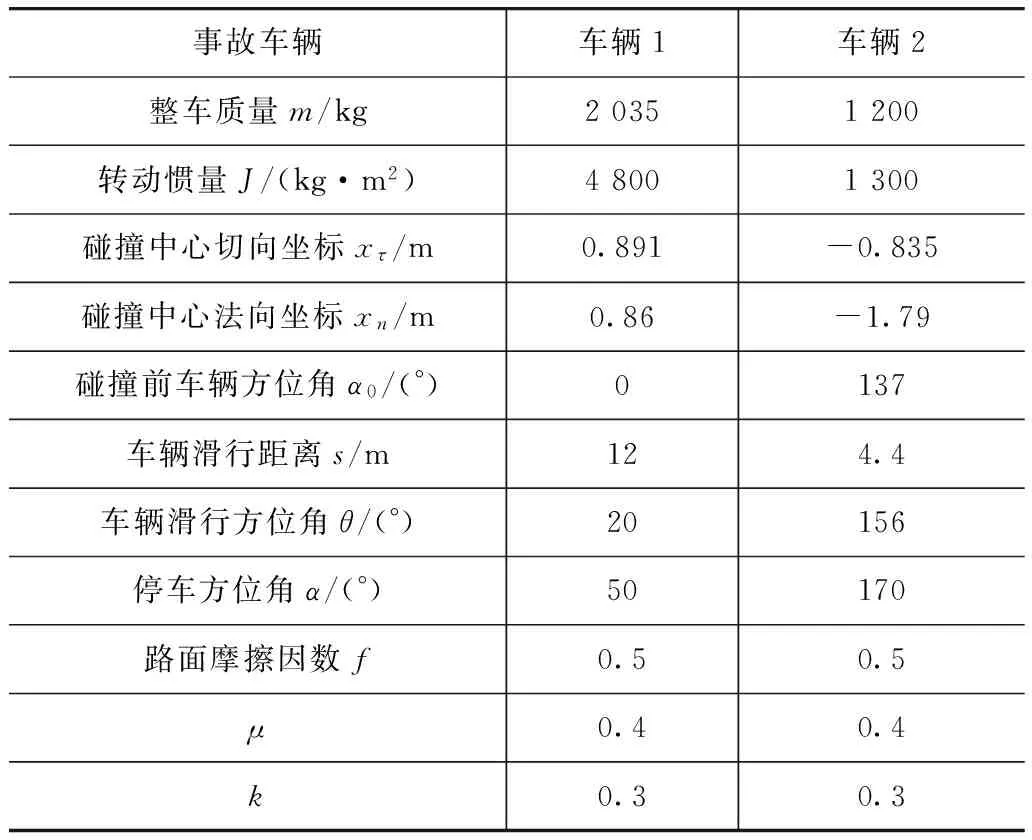
表3 现场勘查数据

由式(2)、式(9)、式(17)和式(23)计算4个模型的A0j和Aj；根据表3，由式(25)～式(27)计算碰撞后车速向量，v1=v2=v3=v4=(-3.709,10.1904,-2.6709,-6.0,0.7882,0.8591)T；由式(1)、式(8)、式(16)和式(22)计算碰撞前车速向量，v01=v02=v03=v04=(-0.23,11.58,-8.58,-8.36,-0.02,0.21)T。两车碰撞前车速v10=3.6×[(v10n)2+(v10τ)2]1/2=41.70km/h，v20=3.6×[(v20n)2+(v20τ)2]1/2=43.13km/h；两车碰撞前车速方位角为α10=arctan(v10n/v10τ)=-1.14°，α20=arctan(v20n/v20τ)=45.74°。结果表明，当A0j中系数没有误差时4个模型的计算结果相同。假定μ和k为易产生误差的模型系数，且μ=0.4和k=0.3为准确值，检验当μ和k存在1%误差时[2]，改进模型控制碰撞前车速误差的可靠性。Δμ和Δk表示μ和k的误差，可能的误差形式如下：①Δμ=0.004,Δk=0.003；②Δμ=-0.004,Δk=0.003；

③Δμ=0.004,Δk=-0.003；④Δμ=0.004,Δk=0；

⑤Δμ=-0.004,Δk=0；⑥Δμ=-0.004,Δk=-0.003；

⑦Δμ=0,Δk=0.003；⑧Δμ=0,Δk=-0.003。

以误差形式①为例，4个模型碰撞前车速误差的计算过程如下。

由式(2)，计算A01和A1；v1=(-3.709,10.1904,-2.6709,-6.0,0.7882,0.8591)T；

(28)

将δA01中第6行元素依次用0,0,0,0,0,0替代后得到δA1。

由式(24)，‖δv01‖/‖v01‖=0.2736。

由式(9)，计算A02和A2；v2=(-3.709,10.1904,-2.6709,-6.0,0.7882,0.8591)T；

(29)

其中：

Δb61= -Δk-0.5km1[(Δx1nτ/J1)+(Δx2nτ/J2)]-

0.5Δkm1{[(x1nτ+Δx1nτ)/J1]+[(x2nτ+Δx2nτ)/J2]}

Δb63= Δk+0.5km2[(Δx1nτ/J1)+(Δx2nτ/J2)]+

0.5Δkm2{[(x1nτ+Δx1nτ)/J1]+[(x2nτ+Δx2nτ)/J2]}

Δx1nτ=-Δμx1τx1n；Δx2nτ=-Δμx2τx2n

将δA02中第6行元素依次用Δc61,0,Δc63,0,Δc65,Δc66替代后得到δA2。

Δc61= -0.5km1[(Δx1nτ/J1)+(Δx2nτ/J2)]-

0.5Δkm1{[(x1nτ+Δx1nτ)/J1]+[(x2nτ+Δx2nτ)/J2]}

Δc63= 0.5km2[(Δx1nτ/J1)+(Δx2nτ/J2)]+

0.5Δkm2{[(x1nτ+Δx1nτ)/J1]+[(x2nτ+Δx2nτ)/J2]}

Δc65=-Δkx1τ；Δc66=Δkx2τ

由式(24)，‖δv02‖/‖v02‖=0.0226。

由式(17)，计算A03和A3；v3=(-3.709,10.1904,-2.6709,-6.0,0.7882,0.8591)T；

(30)

其中：

Δb61= (k+Δk)(m1Δxnτ/J2)-Δk[1+(m1/m2)-

(m1xnτ/J2)]

Δb65=Δk[x1τ+x2τ(J1/J2)]

Δxnτ=-Δμx2τ(x1n-x2n)

将δA03中第6行元素依次用Δc61,0,Δc63,0,Δc65,Δc66替代后得到δA3。

Δc61= (k+Δk)(m1Δxnτ/J2)-Δk[(m1/m2)-

(m1xnτ/J2)]，Δc63=-Δk，Δc65=Δkx2τ(J1/J2)

Δc66=Δkx2τ

由式(24)，‖δv03‖/‖v03‖=0.0777。

由式(23)，计算A04和A4；v4=(-3.709,10.1904,-2.6709,-6.0,0.7882,0.8591)T；

(31)

其中：

Δb63= (k+Δk)(m2Δx1nτ/J1)+Δk[1+(m2/m1)+

(m2x1nτ/J1)]

Δb66=-Δkx2τ；Δx1nτ=-Δμx1τx1n

将δA04中第6行元素依次用Δc61,0,Δc63,0,Δc65,Δc66替代后得到δA4。

Δc61=Δk

Δc63= (k+Δk)(m2Δx1nτ/J1)+Δk[(m2/m1)+

(m2x1nτ/J1)]

Δc65=-Δkx1τ；Δc66=0

由式(24)，‖δv04‖/‖v04‖=0.0495。

同理，可以得到误差形式②～误差形式⑧的碰撞前车速误差(表4)。

表4 碰撞前车速误差

由表4可知，应用4个模型计算了8种系数误差形式所对应的碰撞前车速误差。应用模型计算的碰撞前车速误差和范围最大，为9.09%～27.36%；应用第一改进模型计算的碰撞前车速误差和范围最小，为1.61%～3.86%。由于两车质量比m2/m1=0.59，最接近第一改进模型的适用范围，因此，用第一改进模型能够有效控制碰撞前车速误差。

5 结论

针对模型病态问题的几何特征，应用线性空间与内积空间理论能够准确锁定模型中存在线性相关性的方程；通过对这些方程进行数学变换，在模型病态范围m2/m1≈1，m2/m1>>1和m2/m1<<1内建立对应的改进模型。实例检验结果表明，当m2/m1=0.59，且μ和k存在1%误差时应用改进模型能够将碰撞前车速误差控制在合理的范围内。因此，在病态范围内应用改进模型能够解决模型病态问题。所建立的模型病态问题处理方法为解决此类矩阵模型病态问题提供了值得借鉴的经验。

[1] 姜华平,何宏宇,吴伟阳.正面碰撞事故中车速推算的改进算法研究[J].汽车工程,2009,31(6):531-534.

[2] GA/T643—2006典型交通事故形态车辆行驶速度技术鉴定[S].北京:中国标准出版社,2006.

[3] ZHOU Jing, PENG Huei, LU Jianbo. Collision model for vehicle motion prediction after light impacts[J]. Vehicle System Dynamics,2008,46(S1):3-15.

[4] 李江.交通事故力学[M].北京:机械工业出版社,2000:119-128.

[5] 陈涛,魏朗,龚标,等.车对车碰撞事故再现系统的参数敏感度分析[J].汽车工程,2012,34(9):771-776.

[6] 张健,张鑫.力学参数误差对碰撞前车速的影响[J].西南交通大学学报,2011,46(2):259-263.

[7] CLIFF W E, MONTGOMERY D T. Validation of PC-Crash-A momentun-based accident reconstruction program[C]. SAE Paper 960885.

[8] PIOTR S, JAN U, WOJCIECH W. SMASH program for car accident simulation[C]. SAE Paper 2000-01-0848.

[9] 姜家辉.矩阵理论基础[M].大连:大连理工大学出版社,1995:28-34.

[10] 许洪国.汽车事故工程[M].北京:人民交通出版社,2004:68-90.

[11] 张建.汽车碰撞事故模型病态性处理方法的研究[D].长春:吉林大学,2007.

[12] 张健,张鑫,李江,等.典型汽车碰撞事故自选参数的敏感性分析[J].汽车工程,2012,34(10):905-908.

Cause Analysis and Solution of Ill-posed Problemsin Typical Vehicle Collision Model

Zhang Jian1, Zhang Xin2, Liang Chao1& Li Jiang3

1.CollegeofAutomobileandCivilEngineering,BeihuaUniversity,Jilin132013; 2.ChinaCommunicationsPressCo.,Ltd.,Beijing100011;3.CollegeofTransportation,JilinUniversity,Changchun130022

For solving the ill-posed problems in typical vehicle collision model, the theories of linear space and inner product space is applied to calculate the angle between any two equations in the model according to the geometric feature of the problems. The results show that ill-posed problems are caused by the strong linear correlation among some equations in the model. Improved models can be developed in ill-posed ranges by mathematical transform on equations with strong linear correlation. The perturbation theory is also applied to establish a method for examining the reliability of improved model. The results of an example examination show that when the errors of model parameters are within 1% in ill-posed ranges, the error of pre-impact speed in the improved models can be controlled within a reasonable range, demonstrating that ill-posed problems can be solved by creating improved models in ill-posed ranges.

vehicle collision model；ill-posed problem；error；perturbation theory

*国家自然科学基金(51178001,31570556)和吉林市科技发展计划项目(20090404)资助。

原稿收到日期为2015年6月11日，修改稿收到日期为2015年11月19日。