计及负荷电压静态特性的电力系统最小负荷裕度的快速评估

朱永强，刘光晔，廖庭坚，雷 强



计及负荷电压静态特性的电力系统最小负荷裕度的快速评估

朱永强，刘光晔，廖庭坚，雷 强

(湖南大学电气与信息工程学院，湖南 长沙 410082)

负荷裕度是静态电压稳定性最重要指标之一，定义了非线性复变电力系统的最小负荷裕度。利用非线性电路动态等值方法，引入功率参变量，构造拉格朗日函数。证明非线性电力网络负荷节点获取极大有功功率的必要条件：负荷静态等值阻抗模等于负荷节点看进系统的动态等值阻抗模，然后提出评估电压稳定性的阻抗模裕度指标。同一扰动下，阻抗模裕度越小，电压稳定性越薄弱，节点负荷裕度越小，只需计算最薄弱节点的最大负荷裕度，即系统最小负荷裕度。通过阻抗模裕度最先到达零来确定最薄弱节点获取的极大有功功率，计算其最大负荷裕度。计及负荷功率扰动方式与负荷电压静态特性，通过对IEEE30节点系统的仿真表明：单节点负荷功率扰动方式及恒定阻抗与恒定电流负荷比例的增加，提高了系统的最小负荷裕度。

复变；动态等值；负荷裕度；阻抗模裕度；电压静态特性

0 引言

随着分布式发电的快速发展以及电动汽车的普及，对电压稳定有着重要影响,电压稳定问题一直是电力研究者关注的问题[1-3]。负荷裕度是电压稳定的静态分析指标之一，可快速有效评估系统静态电压稳定性。电力工作者通过负荷裕度确认系统当前运行状态，提前采取适当措施防止电压崩溃发生。电压崩溃与分岔密切相关，鞍结分岔(Saddle Node Bifurcation，SNB)为分岔种类之一。截至今日，鞍结分岔已经得到广泛的分析与研究[4-5]。有功极大值对应着PV曲线鞍结分岔点，鞍结分岔点以上部分为电压稳定区，以下部分为不稳定区。当前运行点距电压崩溃临界点(SNB)的距离即为本文要计算的负荷裕度指标[6-7]，反映了系统对负荷的承载能力。计算负荷裕度的方法有许多，例如二次曲线拟合与非线性灵敏度结合法[8]以及崩溃点法[9]，还有我们熟知的连续潮流法[10]等。这些方法优缺点各不相同，有些计算精度高，但计算量大，有些计算过程简单，但考虑因素不够全面，或精度不够高。根据鞍结分岔点为负荷有功功率极大值点，采用非线性电路动态等值方法证明了非线性电力网络输送功率达到极限的必要条件：负荷节点等值阻抗的模值等于该节点看进系统的动态等值阻抗的模值。继而参照文献[11]确定阻抗模裕度指标(Impedance Model Margin Index，IMMI)，当负荷节点阻抗模裕度等于零，发生鞍结分岔，从而确定每个电力负荷有功功率极大值和最小值。然后计算每个负荷节点的最大负荷裕度值，分析说明阻抗模裕度最先接近零的负荷节点的最大负荷裕度为系统的最小负荷裕度(Minimum Load Margin，MLM)，该节点即电力网络静态电压稳定性最薄弱节点(The Weakest Node of Voltage Stability，WNVS)。最后计及负荷扰动方式和负荷电压静态特性，通过对IEEE30节点系统仿真，分析负荷扰动方式与负荷电压静态特性对电力系统最小负荷裕度的影响，该法只需潮流雅可比矩阵保存的分解因子表，计算量小，结果准确，更符合实际。

1  最小负荷裕度MLM的定义

电力系统的PV曲线如图1所示。

图1PV曲线

(1)

负荷裕度指标用式(1)表示，从PV 曲线中可以看出, 当系统的电压稳定性越高时，负荷节点当前运行状态下获取的有功功率越小，很显然，通过式(1)计算的负荷裕度越大。当电压稳定性较差，这时接近电压崩溃临界状态；负荷节点当前运行状态下获取的有功功率越大，计算的负荷裕度越小。

要评估负荷节点当前运行状态下的电压稳定水平，必须要将负荷节点当前运行状态下的负荷裕度与负荷节点的最大负荷裕度进行比较，得出当前负荷裕度相对最大负荷裕度的百分比，才能有效评估负荷量的相对余量，从而较准确地评估电压稳定性水平，因此需要求出最大负荷裕度。负荷节点最大负荷裕度计算式为

(2)

每个负荷节点的最大负荷裕度也不一样，最大负荷裕度越大，节点电压稳定性越高，反之，节点电压稳定性越差。因此，在相同的条件下，最大负荷裕度最小负荷节点决定着整个电力系统静态电压稳定程度，才是整个电力系统的最小负荷裕度。

2  IMMI推导及与MLM的关联

采用非线性电路的动态等值方法，在定义系统动态等值阻抗的前提下，把整个系统等效为图2所示的两节点简单电路，电压向量对电流向量的导数就是动态等值阻抗。

图2 电力系统综合动态等效电路

Fig. 2Power system comprehensive dynamic equivalent circuit

文献[12]在解析复变函数满足Cauchy-Riemann方程的基础上，对解析复变系统负荷取极大值的必要条件进行了分析计算。但电力系统是非线性非解析复变系统，不满足Cauchy-Riemann方程，此时电压向量不能直接对电流向量求导，因此取负荷节点注入功率控制系数为参变量，则得综合动态等值阻抗为

(4)

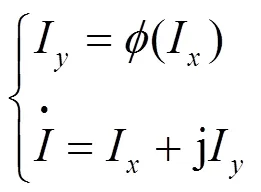
将式(4)改写为

(6)

由式(3)、式(5)、式(6)得动态等值阻抗为

(8)

图2所示负荷节点获取的功率为

(9)

假设负荷功率因数恒定，则约束方程为

(11)

(13)

式(14)两边同时开算术平方根，有

(15)

由此证明了负荷节点获取极大有功功率的必要条件是负荷的静态等值阻抗与负荷节点看进去的动态等值阻抗相同。参照文献[11]定义阻抗模裕度指标IMMI，具体为

3  计及负荷电压静态特性MLM的求取

负荷的电压静态特性对电力系统的电压稳定性有着极其重要的影响[13]，因此考虑负荷的电压静态特性来分析负荷节点的负荷裕度非常必要。负荷的电压静态模型为

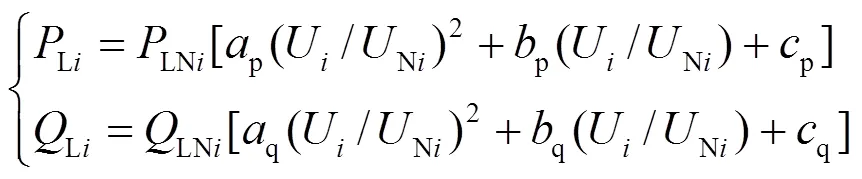
注入节点的功率可表示为

设系统潮流方程为

(19)

注入负荷节点电流方程为

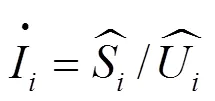
负荷节点静态等值阻抗为

(21)

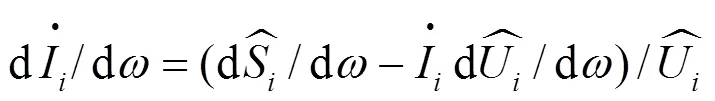
(23)

由式(23)可得

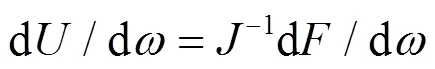
由式(5)、式(22)、式(24)可得动态等值阻抗为

(25)

通过式(18)、式(21)、式(25)计算任意负荷水平下的静态等值阻抗及负荷节点看进去的动态等值阻抗，代入式(16)，即可计算每一个负荷节点的阻抗模裕度，阻抗模裕度最小，且接近零时的负荷节点的最大负荷裕度即为MLM。

4  仿真计算

4.1 不考虑负荷的电压静态特性

采用IEEE30节点系统进行仿真计算，扰动为同步功率扰动及单节点扰动两种方式。

1) 所有负荷采用恒定功率模型，负荷扰动采用同步功率扰动，采用相对基态功率同等比例的增长方式。计算出各个PQ节点在每一个同步功率扰动下的阻抗模裕度，确定阻抗模裕度最先到达零的负荷节点的基态有功功率及此时的极大有功功率，并最终计算电力系统最小负荷裕度，其具体结果见表1。

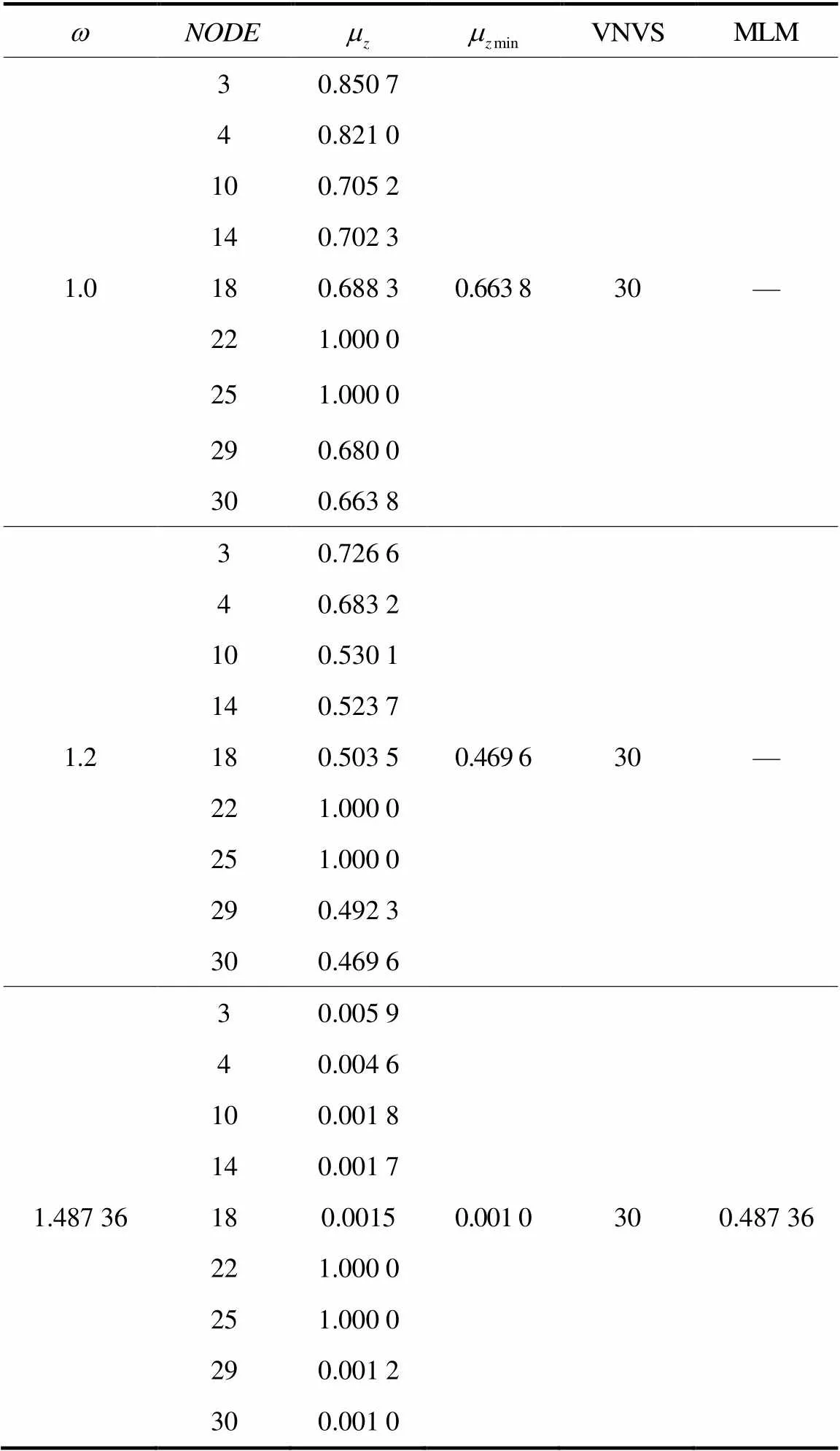
表1 同步功率扰动PQ节点阻抗模裕度及最小负荷裕度

由表1可知，无论负荷功率扰动强弱，节点30的阻抗模裕度最小，为电压稳定性最薄弱节点，负荷裕度最小。随着所有负荷节点功率的逐渐增加，大部分负荷节点的阻抗模裕度逐渐减小，只有极少的负荷节点阻抗模裕度几乎不变，如节点22、25，从结构图看出，它们离发电机比较近，因此比较稳定。当负荷增长系数为1.487 36时，节点30的阻抗模裕度为0.001，十分接近0，此时的有功功率可以被近似地作为节点30的最大有功功率。由式(1)计算其最大负荷裕度为0.487 36，即整个系统的最小负荷裕度为0.487 36。与文献[14]提出的静态电压稳定约束条件下的混合算法计算出的最小负荷裕度相差不大。由结构图看出，节点30离发电机较远，因此电压稳定较薄弱也是合理的，至于节点3、4离发电机更近，却不是最薄弱节点，这与它们的负荷量较重有关。所以，可以通过在负荷裕度较小的节点补偿无功功率或减小节点的负荷量来提高负荷节点的负荷裕度。

2) 采用单个节点进行扰动，即只对被研究的PQ节点进行负荷扰动，扰动功率相对基态功率逐步增长，其他节点的功率保持不变。在同步功率扰动下，得出节点30负荷裕度最小，为系统电压稳定最薄弱节点，单独对其进行扰动，计算各个PQ节点的阻抗模裕度及电力系统最小负荷裕度，其具体结果见表2。

表 2 单节点扰动PQ节点阻抗模裕度及系统最小负荷裕度

将表2与表1的结果进行比较，单个节点扰动时，各PQ节点的阻抗模裕度比同步负荷功率扰动时大很多，且系统的最小负荷裕度远大于同步负荷功率扰动时的最小负荷裕度，为1.259 41。也说明单节点扰动方式下，系统对PQ节点电压有更强的支持能力。

4.2 考虑负荷的电压静态特性

由于30节点是负荷裕度最小的节点，因此采用不同比例的ZIP负荷模型，单独计算节点30的最大负荷裕度，即电力系统最小负荷裕度，具体结果见表3。

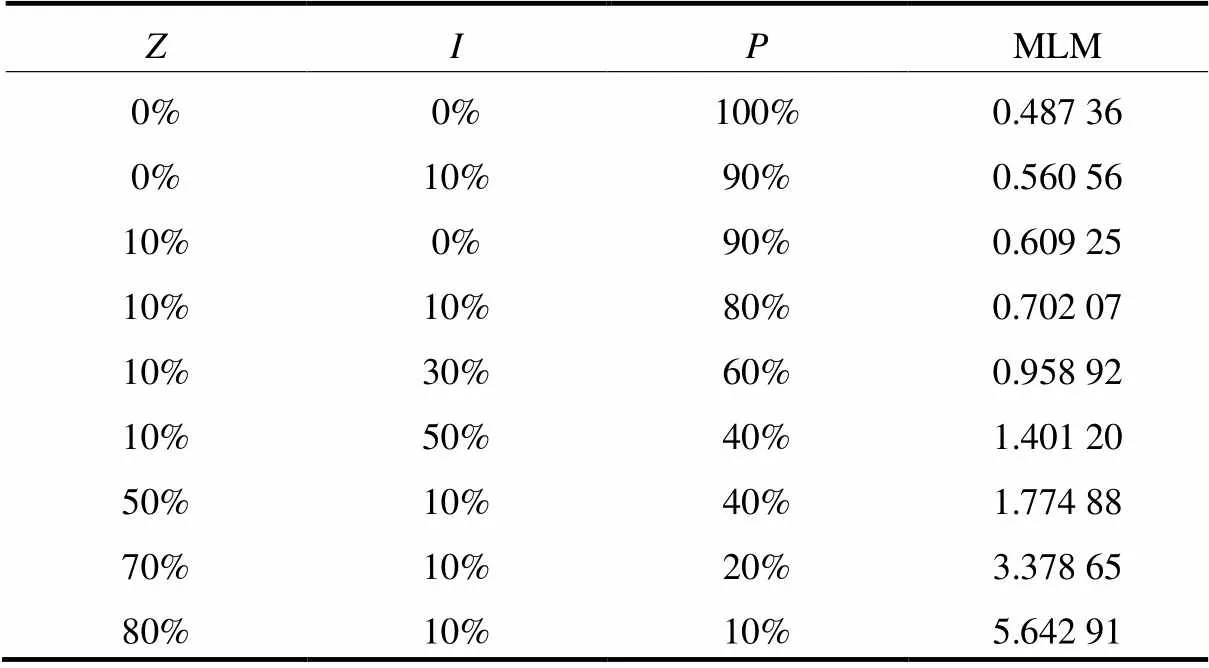
表3 不同负荷比例下电力系统的最小负荷裕度

由表3可知，当负荷采用最保守的恒定功率模型时，系统的最小负荷裕度是最小的。随着恒定电流和恒定阻抗负荷比例的不断增加，最小负荷裕度是逐渐增加。可见，增加恒定阻抗和恒定电流负荷的比例，可以提高系统的最小负荷裕度，进而提高系统的电压稳定性。我国的电力系统负荷均采用的是综合负荷，考虑负荷静态特性更符合实际。

5  结论

阻抗模裕度指标可以评估负荷节点的电压稳定性，越小电压稳定性越差，负荷裕度越小。因此在同一扰动下，阻抗模裕度最小的节点是系统的最小负荷裕度节点，只需计算阻抗模裕度最小的负荷节点的最大负荷裕度。阻抗模裕度为零时，系统达到鼻形曲线的鞍结分岔点，负荷获取了最大的有功功率。通过对IEEE30节点系统的仿真计算表明，单节点负荷功率扰动方式下，系统有更强的电压支持能力，恒定阻抗和恒定电流负荷比例的增加可以提高系统的最小负荷裕度。还可通过在最小负荷裕度节点补偿无功或减小负荷来提高电力系统的稳定性。该方法只用到了潮流计算的雅可比矩阵保存的因子表，计算量小，计算速度快，理论简单直观。

[1] 张勇, 罗滇生, 范幸, 等. 非解析复变电力系统动态无功点优化配置[J]. 电力系统保护与控制, 2015, 43(8): 28-34.

ZHANG Yong, LUO Diansheng, FAN Xing, et al. Optimization configuration of dynamic reactive power point for non-analytical complex variable power system[J]. Power System Protection and Control, 2015, 43(8): 28-34.

[2] 肖助力, 龚仁喜, 陈双. 一种改进不完全S变换的电压暂降检测方法[J]. 电力系统保护与控制, 2015, 43(9): 62-68.

XIAO Zhuli, GONG Renxi, CHEN Shuang. Detection of voltage sag by a modified incomplete S-transform[J]. Power System Protection and Control, 2015, 43(9): 62-68.

第三，加强人民群众的法治观念和法律意识。人民是国家的主人，是依法治国的主体，人民群众法律水平的高低直接影响着依法治国的进程。广大人民群众必须不断提高法律意识和法治观念，自觉的遵守法律，依法维护自己的合法权益，运用法律手段同违法犯罪行为作斗争。

[3] 郑颖, 孙近文, 张冲, 等. 考虑电动汽车接入的配电系统静态电压稳定裕度研究[J]. 电工技术学报, 2014, 29(8): 20-26.

ZHENG Ying, SUN Jinwen, ZHANG Chong, et al. Study of voltage stability margin for the distribution network with electric vehicle integration[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 20-26.

[4] DAI Y, MCCALLEY J D, VIJAY V. Simplification, expansion and enhancement of direct interior point algorithm for power system maximum load ability[J]. IEEE Transactions on Power Systems, 2000, 15(3): 1014-1021.

[5] 衣涛, 王承民, 谢宁, 等. 电力系统的多重(维)鞍结分岔点及其特征分析[J]. 电工技术学报, 2015, 30(20): 145-150.

YI Tao, WANG Chengmin, XIE Ning, et al. Power system multiple saddle-node bifurcation point and its characteristic analysis[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 145-150.

[6] 周玮, 姜汀, 胡姝博, 等. 基于两点估计法的交直流混合系统电压稳定概率评估[J]. 电力系统保护与控制, 2015, 43(5): 8-13.

ZHOU Wei, JIANG Ting, HU Shubo, et al. Probabilistic assessment on voltage stability of AC/DC hybrid system based on two-point estimate method[J]. Power System Protection and Control, 2015, 43(5): 8-13.

[7] 李俊, 邓大上, 房鑫炎, 等. 考虑电压稳定裕度约束的点估计随机最优无功调度方法[J]. 电工技术学报, 2015, 30(7): 27-33.

[8] 罗小春, 李华强, 程超, 等. 基于非线性灵敏度与曲线拟合法的负荷裕度快速算法[J]. 电力系统保护与控制, 2008, 36(15): 50-54.

LUO Xiaochun, LI Huaqiang, CHENG Chao, et al. Fast algorithm based on non-linear sensitivity method combining generalized curved fitting method for loading margin[J]. Power System Protection and Control, 2008, 36(15): 50-54.

[9] DOBSON L. Observations on the geometry of saddle node bifurcationand voltage collapse in electrical power systems[J]. IEEE Transactions onPower Systems, 1992, 39(3): 240-243.

[10]郭瑞鹏, 韩祯祥. 电压崩溃临界点计算的改进零特征根法[J]. 中国电机工程学报, 2000, 20(5): 63-66.

GUO Ruipeng, HAN Zhenxiang. An improved zero eigen value method for point of collapse[J]. Proceedings of the CSEE, 2000, 20(5): 63-66.

[11]刘光晔, 施海亮, 杨以涵. 非解析复变电力系统电压稳定的动态分析方法[J]. 中国电机工程学报, 2013, 33(10): 50-56.

LIU Guangye, SHI Hailiang, YANG Yihan. Comprehensive dynamic analysis method for power system static voltage stability[J]. Proceedings of the CSEE, 2013, 33(10): 50-56.

[12]李帅虎, 曹一家, 刘光晔. 基于阻抗模裕度指标的动态无功补偿装置优化配置方法[J]. 中国电机工程学报, 2014, 34(22): 3792-3794.

LI Shuaihu, CAO Yijia, LIU Guangye. Optimal allocation method of dynamic var compensator based on the impedance modulus margin index[J]. Proceeding of the CSEE, 2014, 34(22): 3792-3794.

[13]李欣然, 贺仁睦, 章健, 等. 负荷特性对电力系统静态电压稳定性的影响及静态电压稳定性广义实用判据[J]. 中国电机工程学报, 1999, 19(4): 26-30.

LI Xinran, HE Renmu, ZHANG Jian, et al. Effect of load characteristics on power system stead-state voltage stability and the practical criterion of voltage stability[J]. Proceedings of the CSEE, 1999, 19(4): 26-30.

[14]张峰, 董晓明, 梁军. 一种求解最小负荷裕度的混合算法[J]. 电力自动化设备, 2013, 33(9): 20-23.

ZHANG Feng, DONG Xiaoming, LIANG Jun. A hybrid algorithm to solve the minimum load margin[J]. Electric Power Automation Equipment, 2013, 33(9): 20-23.

(编辑 周金梅)

Rapid assessment of power system minimum load margin considering load voltage static characteristic

ZHU Yongqiang, LIU Guangye, LIAO Tingjian, LEI Qiang

(College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)

Load margin is one of the most important index in static voltage stability, minimum loadmargin of nonlinear complex variablepower system is defined. Power parameter is introduced using a dynamic equivalence method of nonlinear circuits, Lagrange function is constructed. It is proved the necessary condition of the maximum active power of nonlinear electric power network load node is that load static equivalent impedance mode is equal to dynamic equivalent impedance mode of load node, impedance modulus margin index is put forward which is used for assessing voltage stability. Under the same disturbance, the smaller the impedance module margin is, the weaker the voltage stability is, so the smaller the node load margin is. Therefore, the biggest load margin of the weakest node is calculated, it is minimum load margin. When impedance model margin of the weakest load node is zero, maximum active power is obtained and maximum load margin is calculated. Through simulation on IEEE30 nodes system under different disturbance ways considering load voltage static characteristic, it indicates that single node disturbance way and the increase of constant impedance and constant current load ratio improve minimum load margin of power system. This work is supported by National Natural Science Foundation of China (No. 51577053).

complex variable; dynamic equivalence; load margin; impedance modulus margin; voltage static characteristic

10.7667/PSPC150868

国家自然科学基金资助项目(51577053)

2015-05-23；

2015-07-07

朱永强(1989-)，男，硕士研究生，研究方向为电力系统电压稳定分析与控制；E-mail: 1090321338@qq.com 刘光晔(1960-)，男，博士，教授、博导，研究方向为电力系统分析与控制、输变电技术、铁路牵引供电系统、电力系统继电保护。E-mail: liuguangye@hnu.edu.cn