基于HW D测试的弯沉盆面积指数法及改进

程国勇，雷亚伟，黄旭栋

（中国民航大学机场学院，天津　300300）



基于HW D测试的弯沉盆面积指数法及改进

程国勇，雷亚伟，黄旭栋

（中国民航大学机场学院，天津300300）

摘要：分析了目前国内民航机场刚性道面弯沉测试中的弯沉盆面积指数法，指出其存在的主要问题为反演的基顶模量的不确定性，与美国Ioannides的回归公式所反演的相对刚度半径和基顶模量相差1倍左右；此外其适用的道面板厚度范围缺乏定量指标。针对上述问题，采用有限元方法，分析了156种工况下的理论弯沉。以薄板理论弯沉值为基准，将误差在±10％范围内的数据进行了回归分析，得到修正的弯沉盆面积指数的回归系数。通过对美国联邦航空管理局（FAA）公开的HW D弯沉数据进行反算，表明采用修正后的回归公式反算的基顶模量与真实值之间的误差最大为6.9％。此外，基于薄板理论与有限元方法的计算弯沉值相对误差10％作为标准，提出弯沉盆面积指数法适用的机场刚性道面厚度范围为20～46 cm。

关键词：弯沉盆面积指数法；相对刚度半径；基顶模量；弯沉

采用落锤式弯沉仪（FW D）进行刚性道面结构参数反演是路面结构补强设计和道面结构评价的关键技术之一。反演方法一般可分为弯沉盆逐点拟合法和弯沉盆面积指数法[1]。弯沉盆逐点拟合法一般根据弹性层状理论计算出理论弯沉值，然后假设一组道面结构参数，通过实测弯沉值和理论弯沉值进行逐点比较，将满足弯沉误差标准的道面结构参数作为反演结果，但是该方法不能有效解决相同弯沉盆对应道面结构参数的多解性问题，另一方面弹性层状理论应用于弹性地基板模型时其反演结果的合理性有待验证，因为模型参数存在差异，基本假设也存在差异，所以一般情况下要求正演和反演的结果应基本一致[2]。弯沉盆面积指数法基于弹性地基板理论[3-5]，可以反演刚性道面的弹性模量Er和基层顶面反应模量K，其数学含义是对一个复杂的函数（组）进行反函数求解计算，是一个非常复杂的非线性最优化问题。目前，反演分析方法包括：回归公式法、迭代法、数据库搜索法、遗传算法和人工神经网络法等，并且目前也出现了很多模量反算软件，例如：美国的BOUSDEF程序和ILLIBACK程序、基于弹性层状体系的BISAR、DAMA、CHEVRON丹纳特公司的ELMOD软件以及郑州大学基于系统识别原理的SIDMOD等，但在实际应用中仍存在一些关键技术问题[6-7]。本文基于ABAQUS有限元和FW D实测机场弯沉数据对弯沉盆面积指数法提出几点改进，使Aw与l之间的回归系数更加合理，明确了弯沉盆面积指数法适用的刚性道面厚度范围。

1　弯沉盆面积指数法

1.1原理

威斯特卡德等[8]采用温克尔地基模型，分析了圆形均布荷载作用于无限大板上的挠度与最大弯拉应力等，此外，威斯特卡德还分析了薄板与厚板理论计算结果的差异，提出一种把小半径实际荷载面积放大成当量计算半径b的方法，并给出荷载中心处最大挠度的解析式（1）。袁捷[9]分析了有限尺寸道面板受荷时，距其边缘大于0.7 m的范围可以忽略板的尺寸效应对挠度的影响。所以可以用有限元模拟有限尺寸道面板下受圆形均布荷载作用的响应方程，反算道面板的结构参数。根据弹性地基薄板的弹性曲面微分方程，温克尔地基的挠度解析解为式（2）和相对刚度半径解析解为式（3）。即

其中：w（r）为距离圆形均布荷载中心处的挠度；q为圆形均布荷载的集度；R为圆形均布荷载的半径；D为薄板的弯曲刚度；k为地基反应模量；l为温克尔道面板的相对刚度半径；J0、J1为0阶和一阶贝塞尔函数；t为积分变量；E为道面混凝土的弹性模量；μ为道面板的泊松比。

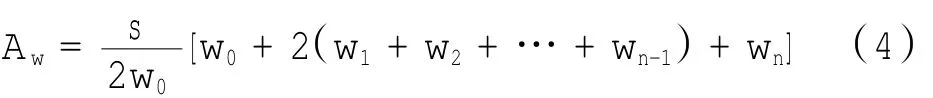
其中：s为测点之间的间距；w0为中心传感器的挠度；wn为第n个传感器的挠度，n = 1，2，…。

1.2存在的问题

中国《民用机场道面评价管理技术规范》（2009-06-11发布）附录D中明确规定了FW D弯沉盆的道面结构参数反演分析方法，其中FW D的加载盘直径为30 cm，传感器间距为30 cm，并给出了距离荷载中心1.5 m范围内弯沉盆面积指数，如图1所示，其计算公式为

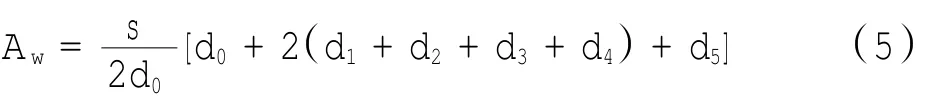
其中：Aw为用于道面板结构参数反演的弯沉盆面积指数（m）；s为传感器之间的间距，取值0.3 m；d0为荷载中心处的弯沉值（m）；di第i个传感器的弯沉值（m）。

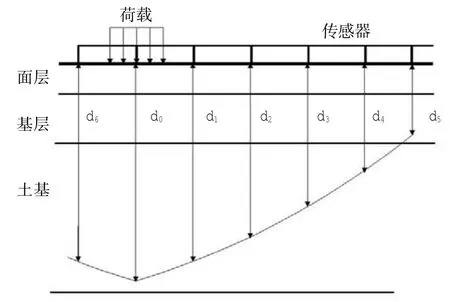
图1　FW D测得的弯沉盆Fig.1 Deflection basin m easured by FW D

由弯沉盆面积指数Aw确定道面结构相对刚度半径l。如果Aw超出图中的取值范围，可由Aw与l之间的多项式回归公式（6）计算l值并给出了回归系数的具体值。即

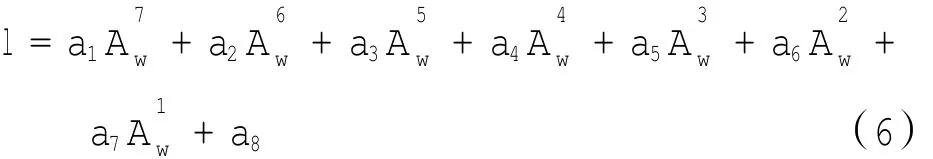
其中：l为温克尔道面板的相对刚度半径；Aw为用于道面板结构参数反演的弯沉盆面积指数（m）；ai为回归系数。

通过实际应用发现，上述方法存在如下问题：

1）基顶模量分析误差

机场水泥混凝土道面计算的力学模型为温克尔地基上的小挠度薄板，弯沉盆面积指数法也从这一理论出发而得出，不同的弯沉盆面积指数法差异仅在于采集弯沉的传感器布置方式不同而导致的公式形式不一样，其分析的结果应当基本一致。但分析国内民航机场道面采用的方法与美国Ioannides[10]弯沉盆面积指数法，并利用美国FAA国家场道试验设施室内模型道面的FW D弯沉数据计算表明，两种方法推算的相对刚度半径l和基层顶面反应模量K差异很大。按照国内规范，相对刚度半径的极差为max（Δl）= 0.08 m，基层顶面反应模量的极差为max（ΔK）= 5 MN/m3；根据美国的Ioannides等人的回归公式，相对刚度半径的极差为max（Δl）= 0.018m，基层顶面反应模量的极差为max（ΔK）= 6 MN/m3。美国Ioannides的回归公式所反演的相对刚度半径和基层顶面反应模量是国内规范的2倍左右。而FAA国家场道试验设施室内模型道面已知的基顶模量K = 72 MN/m3。国内规范和Ioannides[10]弯沉盆面积指数法计算结果如表1所示。

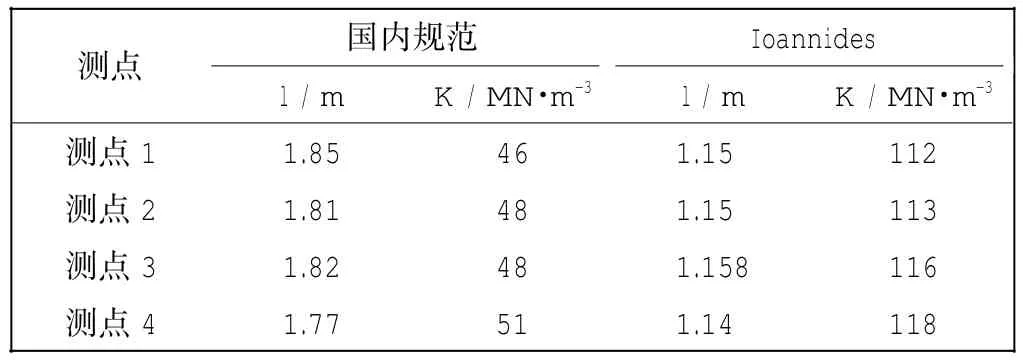
表1　不同测点推算的l和KTab.1 Calculated l and K at differentm easuring points

2）弯沉盆面积指数法适用的道面板厚度范围缺乏定量指标

目前国内规范方法仅规定当弯沉盆面积指数Aw超出曲线图中的取值范围时，可由Aw与l之间的多项式回归公式计算，但并没有对具体适用的道面板厚度范围给出相应的定量指标。

2　弯沉盆面积指数法的改进

为解决以上两个问题，本文采用有限元方法在K地基下，通过改变道面板的厚度、面层材料的弹性模量、地基反应模量和荷载大小等参数并模拟HW D测试过程，分析了156种工况下的理论弯沉数据。

考虑到有限元的求解时间和各实体单元的性能，模型选用C3D8R单元模拟道面板的非受荷区域，采用C3D10单元模拟道面板的圆形受荷区域，用60m×60m有限尺寸的水泥混凝土道面板模拟无限大板，如图2所示。

有限元计算结果表明，当道面板厚度大于50 cm时，HW D荷载盘中心传感器处的计算弯沉值和理论弯沉值存在较大误差，其结果如表2所示。因此，薄板理论解wmax与有限元解d0只有在一定厚度范围内才能近似相等，有限元解d0所依赖的道面本构方程为薄板理论所包含的相关方程，故弯沉盆面积指数法在一定的厚度范围内才更具有适用性。

图2　道面板有限元模型Fig.2 Panel finite elem entm odel

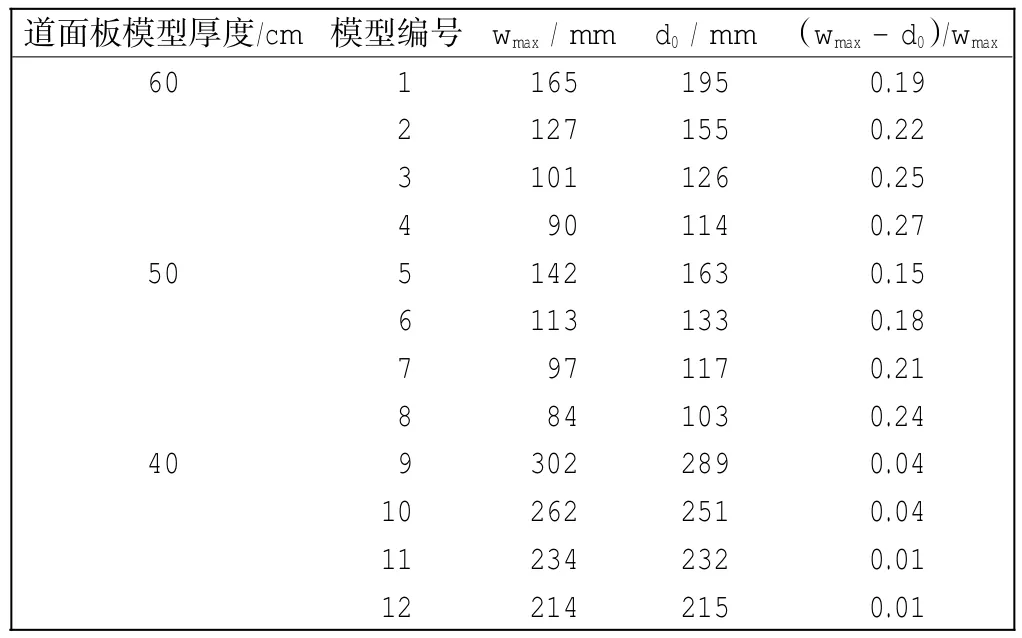
表2　HW D荷载盘中心传感器处的计算弯沉值和理论弯沉值比较Tab.2 Calculation deflected value and theoretical deflection of value com parison at center of HW D load sensor plate

相对刚度半径是一个关于道面材料（Ec，v）、道面板厚度h和基层顶面反应模量k的函数，通过改变以上参数，就可以得到一组相对刚度半径和弯沉盆面积指数，然后对这组数据通过误差分析进行筛选，其控制指标为薄板理论挠度值wmax，挑选出（wmax- d0）/wmax在±10％范围内的数据进行Aw与l之间的多项式回归，如图3所示。采用式（7）的形式对上述计算数据进行回归分析，得到的回归系数如表3所示。

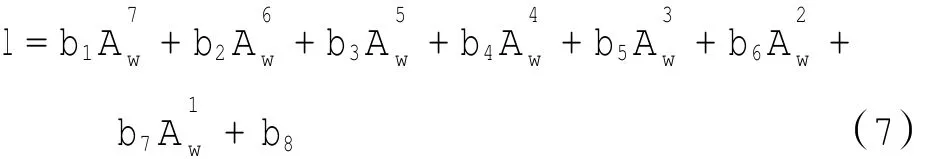
为进一步将目前国内规范、美国Ioannides及式（7）进行比较，分别采用3种回归公式对FAA国家场道试验设施室内模型道面的FW D实测弯沉数据进行分析（已知基顶模量K = 72 MN/m3），这3种公式的不同之处在于美国Ioannides选择近端4个传感器、间距30 cm的方式构造回归关系；国内规范的传感器布置如前介绍，其回归关系通过大量试验数据所得；式（7）模拟国内规范中传感器的布置方式，其回归关系是通过有限元分析所得。对比结果如表4所示，由于回归关系的不同，其反演结果相差很大，但不难发现本文式（7）计算的K值最接近真实情况。

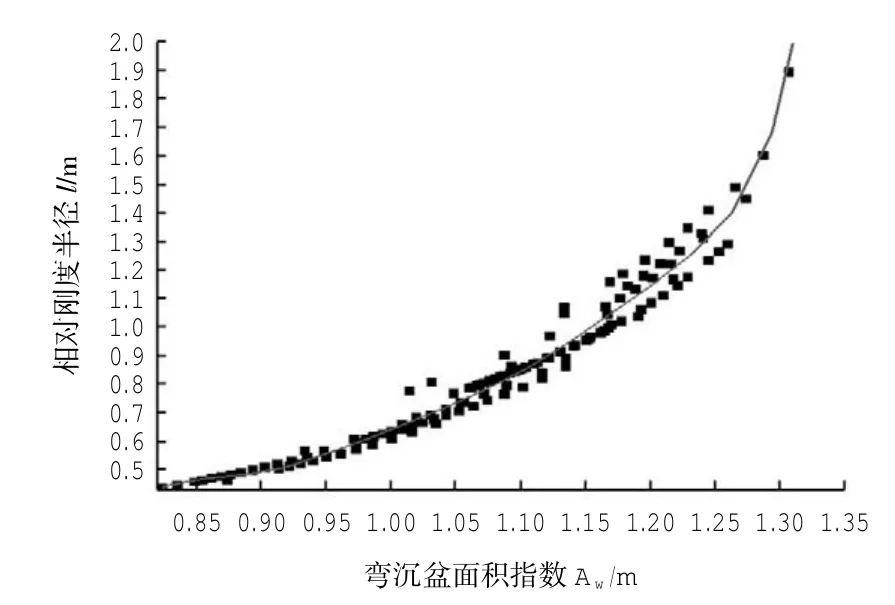
图3　弯沉盆面积指数Aw与相对刚度半径l之间的回归关系Fig.3 Deflection basin area index regression relationships between Awand l

表3　弯沉盆面积指数Aw与相对刚度半径l之间的回归系数Tab.3 Deflection basin area index regression coefficient between Awand l

表4　3种回归公式下推算的K值Tab.4 K values calculated by 3 regression form u la

至于弯沉盆面积指数法适用的道面厚度范围，从156种道面板有限元模型分析结果可以发现，用薄板理论挠度值wmax作为控制指标，（wmax- d0）/wmax作为判定标准，道面板厚度在20～46 cm时，其判定标准都在10％以内，当道面板厚度大于46 cm时，其判定标准都大于10％，不妨把弯沉盆适用的厚度最大值作为临界厚度，其值取为46 cm，此外，根据飞行区指标Ⅱ为A、B时不应小于200 mm，飞行区指标Ⅱ为C、D、E、F时不应小于240 mm，故弯沉盆面积指数法适用的机场刚性道面厚度范围为20～46 cm，如图4所示。

3　结语

1）分析了目前应用最广泛的弯沉盆面积指数法反演道面参数的基本原理，针对国内规范Aw与l之间的回归系数ai不能充分反映道面结构真实状况的问题，基于ABAQUS有限元，对比分析国内规范、美国Ioannides和有限元3种回归公式对真实道面模量的反演，结果表明使用ABAQUS有限元回归的Aw与l的系数bi的弯沉盆面积指数法，其推算的基层顶面反应模量K更接近真实值，最大误差为6.9％。

图4　板厚与（wmax- d0）/wmax之间的关系Fig.4 Relationship between thicknesses and（wmax- d0）/wm ax

2）在温克尔地基下，用薄板理论挠度值wmax作为控制指标，（wmax- d0）/wmax作为判定标准，发现在板厚为46 cm时，判定标准迅速增大，基于有限元分析结果首次定量给出弯沉盆面积指数法适用的道面厚度，其范围为20～46 cm；首次定义了弯沉盆适用厚度的最大值作为临界厚度，在机场刚性道面评价中，其值为46 cm，为以后的道面结构性评价提供了可靠的参考。

参考文献：

[1]姚祖康.水泥混凝土路面设计[M].合肥：安徽科学技术出版社，1999.

[2] AC 150/5320—6D，AirportPavementDesign and Evaluation[S].

[3] JTG D40—2002，公路水泥混凝土路面设计规范[S].

[4]中国民用航空局.MHT 5004—2010，民用机场水泥混凝土道面设计规范[S].北京：人民交通出版社，2010.

[5]中国民用航空局.MHT 5024-2009，民用机场道面评价管理技术规范[S].北京：人民交通出版社，2009.

[6] FederalHighway Administration.Back-calculation of Layer Parameters for LTPP Test Sections，Volume I：Slab on Elastic Solid and Slab on Dense-liquid Foundation Analysisof Rigid Pavements[R].W ashington DC：Departmentof Transportation，2001.

[7]林小平.刚性路面弯沉盆面积指数反演改进方法[J].中国公路学报，2009（5）：14-19.

[8]张福范.弹性薄板[M].2版.北京：科学出版社，1984.

[9]袁捷.机场刚性道面结构参数反演方法研究[D].上海：同济大学，2008.

[10] IOANNIDES A M.Dimensional analysis in NDT rigid pavement evaluation[J].JournalofTransportation Engineering，1990，116（1）：23-36.

（责任编辑：杨媛媛）

Deflection basin area index m ethod and im provem ent based on HW D test

CHENG Guoyong，LEIYawei，HUANG Xudong
（Airport Engineering College，CAUC，Tianjin 300300，China）

Abstract：The deflection basin area index method in deflection tests of rigid pavement of current domestic civil aviation airports is analyzed，pointing out that itsmain problem is the uncertainty of inversion basemodulus，which has a one-time difference from radii of relative stiffness and base modulus back calculated by the American Ioannides' regression formula.Besides，the thickness range of pavement slab applied to thismethod is lack of quantitative index.According to the above problems，finite elementmethod is used to analyze the theoretical deflection data under 156 working conditions.Based on deflection value of the thin plate theory，regression is employed to analyze test data within the error range of 10％，modified regression coefficient of the deflection basin area parameterscan be obtained.By back-calculating the public HW D deflection data of America FAA，it shows that themaximum error is 6.9％ between the real value and the basemodulus back calculated with the modified regression formula.In addition，based on the thin plate theory and finite elementmethod，10％ relative errors of deflection value are chosen，puting forward that the thickness range ofairport rigid pavement is20～46 cm applied to deflection basin area parametersmethod.

Key words：deflection basin area indexmethod；relative stiffness radius；basemodulus；deflection

作者简介：程国勇（1971—），男，河北衡水人，教授，博士，研究方向为机场工程、岩土工程.

基金项目：国家自然科学基金项目（51178456）；中国民航大学机场工程科研基地开放基金项目（KFJJ2012JCGC01）

收稿日期：2014-12-15；修回日期：2015-03-14

中图分类号：U416

文献标志码：A

文章编号：1674-5590（2016）01-0032-04