基于GA—RS—LR算法的公司财务与个股投资探究

2016-04-08瞿尚薇王斌会

经济数学 2016年1期

瞿尚薇　王斌会

摘要运用遗传算法粗糙集逻辑回归方法（GARSLR）探讨我国A股上市公司财务与股票收益的关系.运用GARS方法获得财务指标最优约简；运用LR模型探求两者关系.最终，经GARS约简，60个财务指标中有17个对股票投资有重要影响；通过LR模型，4个指标具有显著效应；其中，负债与权益市价比为5.82%负效应，其余为正效应.对2015年股票相对波动进行预测得到70%的准确率，验证了GARSLR模型对中长期投资的有效性.

关键词遗传算法-粗糙集；逻辑回归；股票收益；公司财务

中图分类号 F224 文献标识码 A

1 引言

股票市场对一个国家和地区的经济发展动向有前导作用.股票收益受到宏观经济现状、政策、公司财务、投资者情绪等因素影响.研究股票收益问题一直是学术界的研究热点.目前，学术界对股价与上市公司财务之间关系的探讨主要从两方面入手.一是通过建立计量模型来探求股票与其影响因素的关系，进而对股价进行分析与预测[1，2].然而计量模型对数据平稳性、正态性等有严格限定，直接利用很难达到预期结果.股票市场数据体量巨大、类型繁多，故很多学者转而选用数据挖掘方法来探究其关系.如有不少学者就运用遗传算法[3]、BP神经网络[4]等得到了较为理想的结果.

粗糙集（Rough Sets）理论[5，6]由波兰数学家Pawlak Z于1982年所提出.这是一种用于处理含糊和不确定信息的新型数学工具，具有优越的知识简化能力.粗糙集理论利用现有知识库对不精确的知识进行近似描述[7].RS方法不需预先假定概率分布，也不需像模糊集理论一样假设模糊隶属函数的结构，而是仅仅利用数据本身提供的信息.目前对粗糙集的研究主要集中于其数学性质，理论的扩展以及与其他智能方法的融合与有效算法等[8].杜婷（2012）将粗糙集运用到了个人信用评估模型之中，并取得了良好的约简结果[9].王刚、杨善林将粗糙集与支持向量机相结合，以分析网络商品评论中的情感进行分析，实证表明，RSSVM方法可以提高网络用户情感分析的准确程度[10].逻辑回归方法由vethulst首次提出.1980年，Ohlson率先将逻辑回归模型用于财务危机预警，分析样本公司在破产概率区间上的分布以及两类错误和分割点之间的关系，并得到高预测准确率[11].刘遵雄、黄志强等（2012）在逻辑回归的基础上进行完善，提出了基于平滑小编绝对偏离（SCAD）惩罚逻辑回归模型，运用到财务预警，实验结果表明SCAD惩罚逻辑回归模型的分类效果更好[12].因此Logistic回归法在经济领域的研究受到了极大关注.

基于此，本文提出了遗传算法-粗糙集-逻辑回归（GARSLR）数据挖掘技术，用于探究股票投资与上市公司财务指标体系的内在联系.运用GARS模型得到最优财务约简指标.并在此之上利用逐步回归法与Logistic回归模型以探究公司财务与股票收益的确切关系.最终得到上市公司财务指标不同大类之间与个股投资概率之间的正负效应关系及其影响大小.

经济数学第 33卷第1期瞿尚薇等：基于GARSLR算法的公司财务与个股投资探究

2 GARSLR模型构建

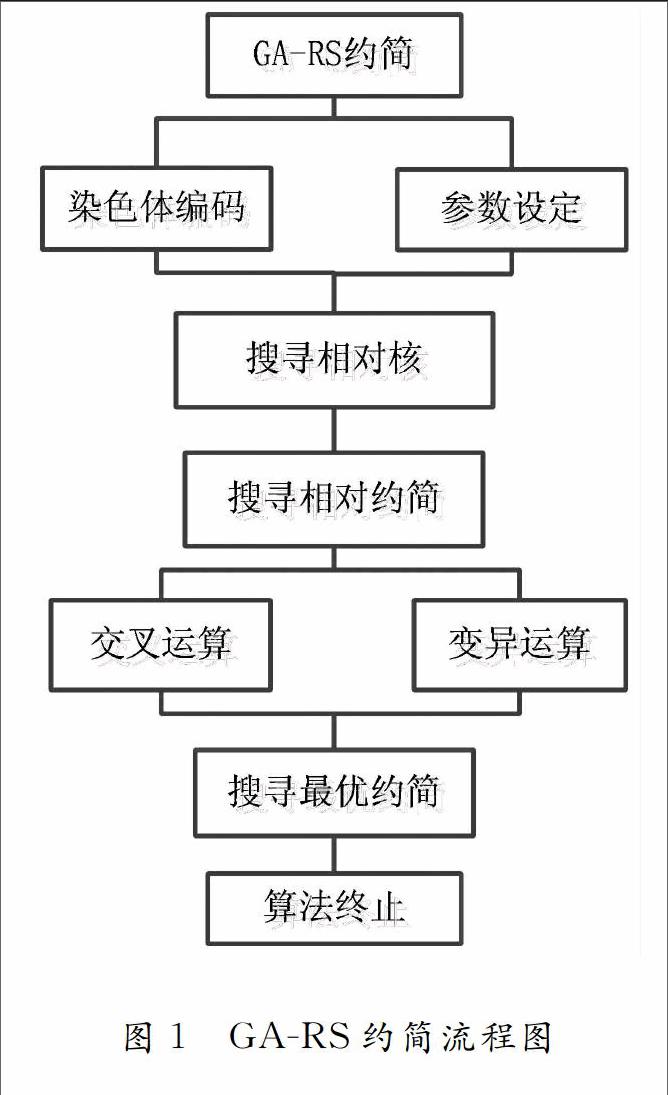
2.1 GARS约简模型

粗糙集理论的属性约简算法可分为是盲目删除属性约简算法与启发式算法.遗传算法作为启发式算法中的一种，具有全局优化和隐含并行的特点，在解决复杂问题中具有明显优势.遗传算法在属性约简问题中需要具体考虑的因素如下：

3 GARSLR模型实证

3.1 数据选取与处理

以我国上海交所与深交所上市的A股上市公司为依据，选取2014年下半年内数据完整、具有不同行业分类的非ST、非*ST的上市公司作为样本.提取公司财务季度指标60个，个股开盘价、收盘价，上证综合开盘指数、收盘指数等指标，最终得到样本913个.其中财务指标体系的分布见表1.

不同指标之间量纲不同，同一指标不同个体之间的差别各异，直接利用原始数据进行分析，不仅会增大模型的复杂度，还会造成结果的不理想.故运用K-均值聚类对各项指标进行逐一聚类，并最终将公司就不同指标分别分为3类.

由于公司财务报表的公布具有时滞性，股票数据选取也将延后一个季度.同时，考虑到投资者投资其他领域而非股票所造成的机会成本，本文用上证综指收益率作为基准收益率：当大盘指数上升时，若个股上升幅度更大，则认为该个股为强势股，值得投资；反之，投资该个股并非明智之举.同理，当大盘指数下降时，若个股下降幅度更小，则该个股是抗压股；反之.基于此将股票分为2类.“好”为具有投资价值的强势股或者抗压股；“差”为不值得投资的股票.

3.2 GARS属性约简

在对离散化数据进行GARS属性约简之前，需要设定遗传算法的参数.具体见表2.

约简后，影响股价相对收益率的财务指标从60个变量缩减为17个.约简集合相对决策属性的依赖度都达到了100%，这表明该约简结果对决策属性的解释度100%.约简后的指标分布见表3.

可知，发展能力指标数目最多，共6个指标；其次是偿债能力.考虑到时滞性，该17个约简指标应是股票价格波动的领先指标，对下期的股价相对波动有着显著的影响.投资者在决策时应重点关注.

3.3 Logistic回归与逐步回归

通过GARS约简后，财务指标得到了极大的简化，但是GARS属性约简只能保证上市公司财务指标属性集对个股相对波动率的相对重要性，而没有给出两者之间更为确切的关系.因而引入LR模型对约简的财务指标与股票波动的相互关系做更为细致准确的刻画.同时，对财务指标体系而言，计算过程中所运用的基础数据有交叉，故指标之间存在很强的相关性.这一缺陷会导致财务指标之间存在比较严重的共线性，如果直接使用LR模型将极大减弱模型的拟合效果.因此，在LR模型中使用逐步回归法进行变量筛选，消除变量之间的共线性，从而精简模型.endprint

通过计算17个约简指标的VIF值可知，固定资产增长率、销售费用本增长率的VIF都超过5，说明变量之间存在共线性.利用逐步回归法得到的LR模型中变量的VIF值见表4.可以发现，此时各变量之间已不存在共线性问题.

为验证模型有效性，以2014年第4季度财务指标为自变量，2015年第1季度股票投资比为应变量进行模型预测检验，得到900个样本的预测准确度为70%.这表明大约有630个上市公司的个股波动可以通过上一期的GARSLR模型得到准确预测.这对价值型的中长期投资者具有一定的参考意义.

4 结论

本文提出了遗传算法-粗糙集-逻辑回归方法（GARSLR）探究股价相对收益率与财务指标的关系.利用K-均值聚类进行离散化处理，既解决了数据量纲不一致的问题，又使同一类别相似个体之间的差异被忽略，而不同类别之间的差异被放大.通过选用GARS方法以约简众多的财务指标.最终得到由17个指标所组成的约简体系，且RS约简的相对依赖度为100%.基于约简指标数据，利用逐步回归法对LR模型进行变量筛选，解决共线性问题.最终得到上市公司财务指标不同大类之间与个股投资概率比之间的正负效应关系及其影响大小，并得到70%的预测准确度，验证了GARSLR模型对中长期投资所具有的优势.

参考文献

[1] 陈玉山，席斌.独立成分分析方法在股票分析中的应用[J].计算机工程与设计，2007， 28（6）： 1473-1476.

[2] 吴荣盛.全流通条件下的股票价格与财务信息的相关性研究-来自我国沪深300指数的实证研究[D].成都：西南财经大学经济学院，2014.

[3] 胡冰，潘福铮，胡清锋.遗传算法在股票短期投资决策中的运用[J].系统工程与实践，2003， 23（2）： 7-13.

[4] 王莎. BP神经网络在股票预测中的应用研究[D].长沙：中南大学商学院，2008.

[5] Z PAWLAK. A Rough Set Perspective [J]. International Journal of Computational Intelligence， 1995， 11（2）： 227-232.

[6] Z PAWLAK， Busse GRZYMALA，J SLOWINSKI， et al. [J]. Communications of the ACM， 1995， 38（11）：89-90.

[7] 董威.粗糙集理论及其数据挖掘应用[M].沈阳：东北大学出版社， 2009.

[8] 王国胤. Rough集理论在不完备信息系统下的扩充[J].计算机研究与发展， 2002， 39（10）： 1238-1243.

[9] 杜婷. 基于粗糙集支持向量机的个人信用评估模型[J]. 统计与决策，2012，1（13）：94-96.

[10]王刚，杨善林.基于RS-SVM的网络商品评论情感分析研究[J].计算机科学，2013，40（11）：274-277.

[11]J OHLSON. Financial ratios and probabilistic prediction of bankruptcy[J]. Journal of Accounting Research， 1980，18（1）：109-131.