天津地铁盾构施工对地表沉降影响的风险评估及精细化控制研究

路　平， 郑　刚, 张稳军， 雷华阳

(1. 天津大学建筑工程学院， 天津　300072； 2. 天津大学滨海土木工程结构与安全教育部重点实验室， 天津　300072)



天津地铁盾构施工对地表沉降影响的风险评估及精细化控制研究

路平1, 2， 郑刚1, 2, 张稳军1, 2， 雷华阳1, 2

(1. 天津大学建筑工程学院， 天津300072； 2. 天津大学滨海土木工程结构与安全教育部重点实验室， 天津300072)

摘要：目前我国城市地铁建设中对地表变形的要求愈加严格，仅依靠工程经验已很难实现。结合天津地铁天津站—建国道站盾构区间试验段的现场监测结果，对掘进过程中盾壳摩擦力、刀盘扭矩、掌子面压力和注浆压力等盾构掘进参数对地表沉降影响进行参数化模拟分析，并针对盾构掘进参数的波动造成的地表沉降计算结果进行风险损失等级的可拓法风险评估，基于风险损失评估结果以及盾构掘进参数实测结果进行统计分析得到风险失效概率，从而计算出各致险因子的风险值并提出相应的精细化控制措施。结果表明： 1)该隧道试验段致险因子按风险值从大到小依次为盾壳摩擦力、注浆压力、掌子面压力、刀盘扭矩； 2)在该区间后续下穿高速铁路的盾构掘进过程中，针对风险值较大的盾壳摩擦力、注浆压力波动制定精细化的风险控制措施，最终使地表沉降稳定在5.1 mm，满足了铁路运营的要求。

关键词：天津地铁； 盾构隧道； 参数化分析； 地表沉降； 可拓法； 风险评估

0引言

截至2014年，我国已有36个城市的轨道交通规划获得批准并开工建设，盾构法作为城市地铁修建的重要工法也得到了广泛的应用；但盾构工程建设中也受到了周围环境的限制与施工控制技术的挑战，如下穿高速铁路时路基沉降的要求不能超过6 mm，故需要采取精细化到毫米级的控制措施，而不能仅仅依靠工程经验。

针对盾构施工对周围环境影响的问题，国内外学者对此开展了许多参数敏感性研究。比如： T. Kasper等[1-2]对盾构掘进过程中土体、注浆体的物理力学性质、覆土厚度、掌子面压力和注浆压力等进行了参数化分析；沈建奇[3]针对盾构在施工过程中的宏观稳态特性以及刀盘切削土体的动态特性，提出了盾构掘进过程的精细化数值模拟方法，实现了对盾构法施工关键参数的预测及对各参数相互关系的分析；R.Hasanpour等[4]利用有限差分法考虑不同千斤顶顶推力作用以及不同掘进速度时，针对双线隧道对冻土地层变形影响进行了研究；徐泽民等[5]描述了天津地铁3号线下穿历史风貌建筑时由于盾壳摩擦过大导致该建筑物产生较大沉降的事故。

另一方面，针对盾构隧道风险管理与控制的研究工作也在不断完善。比如： 2004年，国际隧道协会发布了《隧道风险管理指南》[6]，为隧道工程的风险管理提供了系统的方法与标准；黄宏伟等[7-8]对地铁隧道工程的风险评估与管理方面进行了研究，提出了基于地铁建设与运营不同阶段的风险评估与控制方法，并开发了风险管理软件；安永林[9]、彭立敏等[10-11]对隧道瓦斯突出、塌方、邻近结构物施工的隧道围岩变形安全性能等进行了风险评估，运用突变理论和可拓学理论等开展了应用研究；2012—2014年，我国相继颁布实施《城市轨道交通地下工程建设风险管理规范》[12]和《城市轨道交通工程监测技术规范》[13]，标志着我国对地下工程风险管理与控制的研究具备了可靠的标准化保障。

但目前在针对盾构工程各个阶段对地表沉降影响的研究中，无论对计算结果还是监测结果的评价与控制，人为因素的影响仍占较大比重，且往往停留在对工程整体风险等级的综合评价。可拓法作为可拓学的主要应用之一，为解决实际工程中的评估问题提供了新的客观途径，可以结合现有规范并基于工程计算结果进行更精确的风险评估，尽可能地降低主观因素的干扰，从而对每个致险因子的影响进行定量的描述与排序，制定出更有针对性的预防控制措施，降低工程风险。此外，盾构隧道由于赋存环境不同，其风险评估具有地域差异性，需结合典型地区具体工程建设的特点与需求，这方面研究工作尚存不足。

本文将可拓法应用于盾构掘进对地表沉降影响的风险评估，以天津软土地层深埋盾构下穿铁路为工程背景，结合盾构掘进参数化分析的沉降计算结果以及盾构掘进参数监测数据，针对掘进参数的波动对周围地表沉降影响进行风险损失、风险失效概率定量的风险评估，并提出精细化的风险控制措施。

1可拓法的基本原理

可拓学是由我国学者蔡文[14-15]开创的以物元为基本单位来描述事物可变性的原创性学科。其中，物元是通过以事物、特征以及事物关于该特征的量值所构成的三元组，即R=(事物，特征，量值)。可拓集合的建立是为了研究对象集中不属于经典子集而又能转化得到该子集中的元素，并用关联函数值的大小来衡量元素和集合的关系，分出不同的层次，使得经典集合中的“属于”、“不属于”集合的定性描述发展成为定量描述元素具有性质P的程度及其变化。关联函数的基本公式为

(1)

式中:X0=[a,b]，X=[c,d]，X0⊂X0且无公共端点。可拓集合的关联函数属于(-∞,+∞)，扩展了模糊集合隶属函数只属于[0,1]的运用范围，评判结果更精确[9-11]。

本文提出的基于参数化分析的计算结果采用可拓法进行评价，首先需对试验段的可靠的计算结果进行合理的风险评估，使得对可影响计算结果的参数的评价更具有针对性，从而更合理地指导后续下穿高速铁路的精细化施工。基于参数化分析的可拓法风险评估流程如图1所示。

图1　基于参数化分析的可拓法风险评估流程

Fig. 1Risk assessment flowchart of extension method based on parametric analysis

2影响参数确定

2.1工程背景

天津地铁2号线建国道站—天津站左线区间为深埋盾构区间，期间第96—276环依次下穿铁路机待线、津山线、津秦客专联络线、高速铁路等铁路群，如图2(a)所示，对地表变形控制较为严格。该区间试验段下穿铁路机待线(96—101环)，隧道覆土厚度约18 m，地下水位埋深约1.8 m，盾构断面穿越地层主要为粉黏、粉砂，特别是隧道断面底部较厚的⑦4粉砂层，其渗透系数较大。场地土层分布情况如图2(b)所示，其修正剑桥模型参数为通过对该场地内土体取样进行室内直剪试验和固结回弹试验得出。

(a) 场地及监测布置平面图

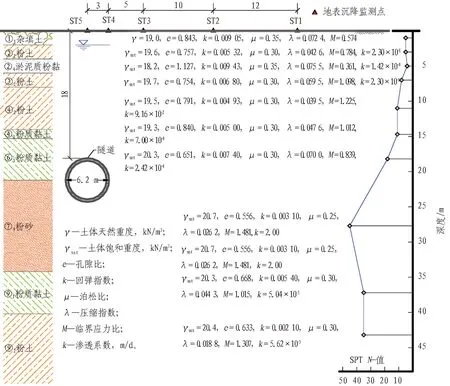
(b) 土层及监测布置剖面图

2.2盾构设备及参数

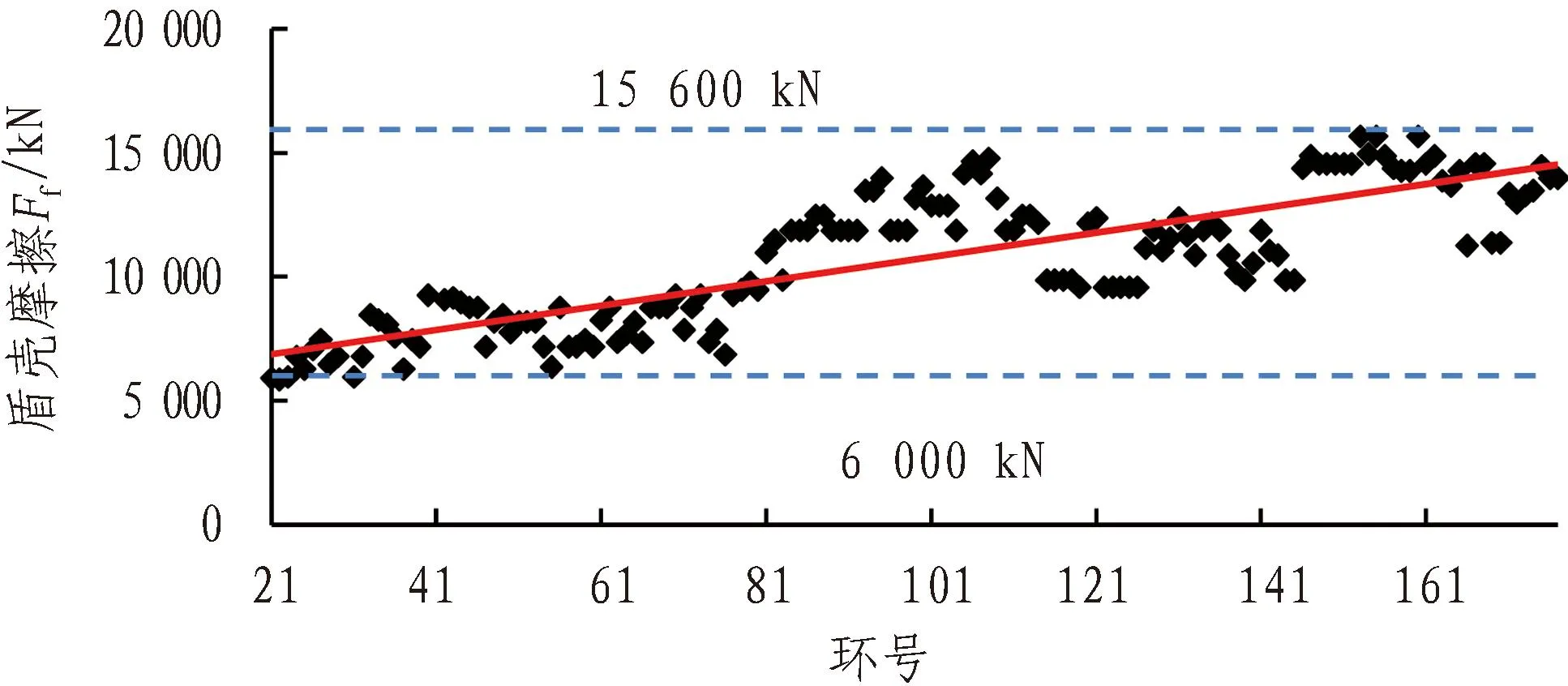
该区间采用加泥式土压平衡盾构，长度为8.4 m，直径为6.4 m，盾壳钢板厚度为30 mm。该盾构可用于管片直径为6.2 m，长度为1.2 m的隧道施工。该区间试验段(21—177环)的盾构掘进参数监测结果如图3所示，分别表示了盾壳摩擦Ff、掌子面压力pN、刀盘扭矩MT、注浆压力pG的变化趋势以及波动范围。

(a) 盾壳摩擦

(b) 掌子面压力

(c) 刀盘扭矩

(d) 注浆压力

3参数化分析

3.1分析模型

本文采用ABAQUS建立可考虑流固耦合的三维有限元模型(如图4所示)，其模拟过程已在文献[16]中详细说明，故本文只进行简要介绍。模型土体的侧向边界和底层边界约束了其法向位移，地下水位位于地表以下1.8 m，并在模型侧面施加了孔压边界条件。模型中重点研究了土体的短期变形，即暂不考虑盾构驶出计算域后土体长期固结的影响。

隧道衬砌(350 mm厚壳单元)采用0.75的抗弯刚度有效率来考虑工程中管片错缝安装的影响，衬砌弹性模量和泊松比分别取25.9 GPa和0.2,厚度为0.03 m的盾构机身也采用线弹性壳单元模拟。根据K. Komiya等[17]的研究，盾构机身的弹性模量采用10倍钢材的弹性模量(2 100 GPa)，泊松比取0.2，以此来将盾构机身等效为刚体。盾尾注浆体的模拟采用等效均质圆环法，注浆体弹性模量取500 MPa，泊松比取0.3[1]，这样注浆体与周围土体的接触压力即为盾尾注浆压力pG[16]。

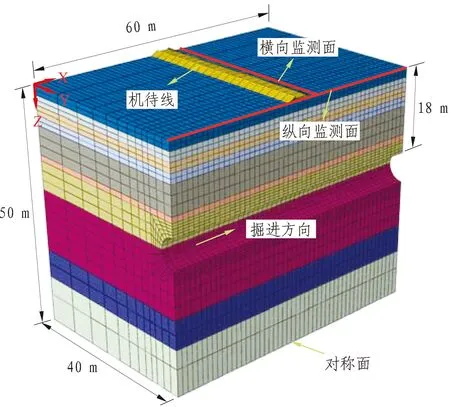
图4　有限元模型示意图

采用“刚度迁移法”来模拟盾构向前推进的过程，即盾构一步一步“跳跃”式推进[4]，推进模拟中暂不考虑管片安装与盾构停机的影响。每次推进长度为一环管片宽度(1.2 m)，盾构中已安装的管片距掌子面的距离为7.2 m。每次掘进后掌子面压力pN、盾壳摩擦力Ff和刀盘扭矩MT都根据该研究区段施工中监测结果的取值范围施加，其施加位置如图5所示。模型中所采用的掘进参数监测结果及其模拟方法均已在文献[16]详细阐述，故只在此简述。

图5　盾构掘进参数施加示意图

盾壳摩擦力Ff为盾构千斤顶总推顶力F与掌子面顶推力FN的差值。用于克服盾壳摩擦力的顶推力简化成均布线荷载，沿盾构掘进方向施加在盾构机身千斤顶安装位置(距掌子面4.8 m)的圆周上。面荷载pN沿深度呈梯形分布，作为掌子面压力施加在隧道掌子面土体上。刀盘正面扭矩MT以刀盘正面切向切削力τ的形式施加在隧道掌子面上，每环推进后切削力变化方向作用在掌子面土体上，以避免盾构自身发生过大的转动。

3.2计算结果

3.2.1结果验证

图6显示了地表横向沉降槽(ST1-9，X=36 m)和纵向沉降槽(SL1-5，Y=40 m)曲线的发展变化。图中同一颜色的点和线分别代表同一施工时刻的实测和计算地表沉降值，可见计算结果和实测结果基本吻合。图6(a)所示的沉降槽分布符合反向的Gaussian分布曲线，计算曲线和实测结果的反弯点分别位于隧道中心线旁10.3 m和9.0 m。计算和实测沉降槽在10月15日(盾尾刚脱出1 d)时有较大的偏差，这是由于偶然升高的二次注浆压力暂时性地抑制了地表沉降的发展。图6(b)所示的沉降槽曲线在X=30 m附近的区段产生了一定程度的反弯，这与J. N. Franzius等[18]描述的纵向沉降槽规律相符。综上，可以验证本文模拟方法得到的沉降计算结果是可靠的。

(a) 横向沉降槽

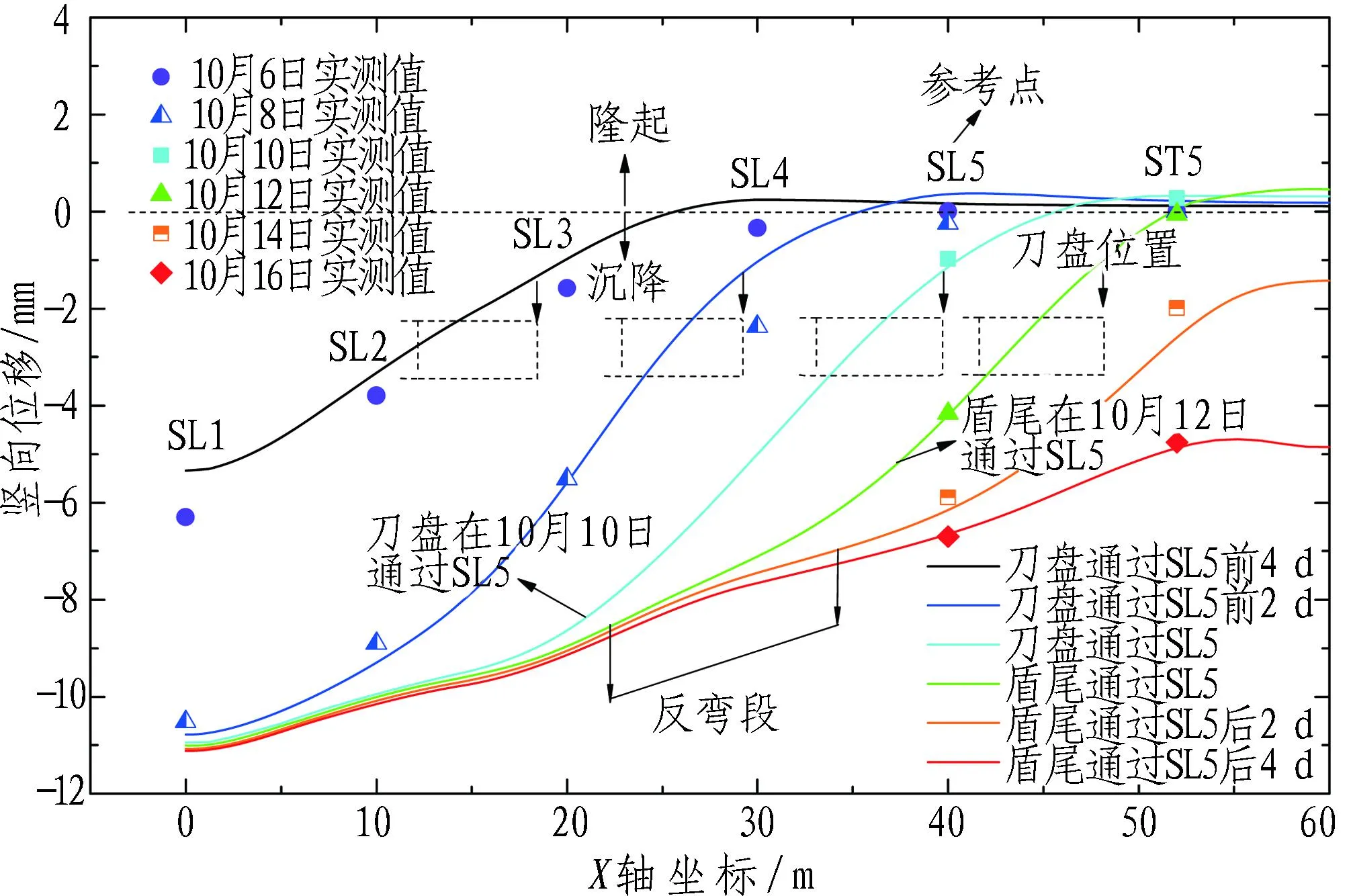
(b) 纵向沉降槽

3.2.2参数化分析计算

实际盾构在掘进过程中，各个盾构力学掘进参数不是恒定不变的，均在一定的取值范围内波动，该取值范围的确定可以通过对图3实测数据的统计得到，并将每个取值范围内等分成5个等级。本文以该盾构区间掘进参数在各自取值范围内变化进行了参数化分析，假定其中一个参数变化时，其余参数保持不变(共20组工况)，以此研究盾构力学掘进参数变化对地表土体沉降的影响，并将盾尾脱出后4 d的计算结果列于表1。

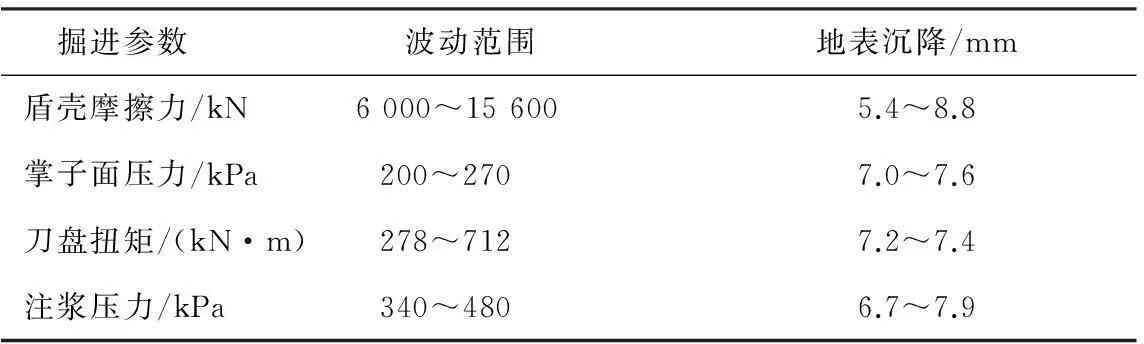
表1　参数化分析中的地表沉降变化

从表1可以看出，盾壳摩擦力在其取值范围内波动对地表沉降影响的变化幅度最大，刀盘扭矩影响最小。这主要是因为： 1)盾壳摩擦力的作用面大小(盾壳侧壁面积176.9 m2)比掌子面压力和刀盘扭矩的作用面(掌子面面积32.2 m2)大4倍，故盾壳摩擦力的影响更易传递到地表； 2)掌子面压力和注浆压力参数自身的相对波动范围远小于盾壳摩擦力； 3)掘进过程中刀盘的转动方向是随着盾构掘进的进行而逐环交替的，从而抵消了一部分刀盘扭矩产生的影响。

4基于参数化分析结果的可拓法风险评估

4.1风险损失评估

4.1.1风险损失等级评估

所谓风险损失，是风险事故发生后产生的一系列影响。本文暂不考虑盾构掘进造成的经济损失、伤亡损失和工期损失，只研究了最直接影响，即地表沉降超过允许限值，或占用了地表沉降的安全储备[19]。这就需要对由各掘进参数波动产生的风险损失的等级进行评估，本文采用可拓法进行评价，该方法可以把是与非的定性描述发展为定量描述，并通过建立多指标的评估模型，来完整评价事物。基于上文对该区间盾构掘进的参数化分析得到的地表沉降结果，将该方法引入盾构掘进过程的风险损失等级评估中，具体如下。

4.1.1.1确定经典域与节域——沉降分级标准

综合天津软土地区盾构实际施工中对地表沉降的控制效果以及参考《城市轨道交通工程监测技术规范》[13]关于盾构下穿铁路时对地表沉降影响程度的界定，将地表沉降的损失等级分成5种等级，得到经典域

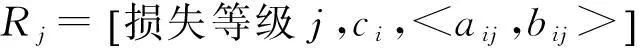
(2)

式中： j =1，2，…m(损失等级级数，m = 5，分别对应于规范[12]中的E，D，…A级)； i=1，2，…n(掘进参数编号，n=4)； c1、c2、c3、c4表示影响损失等级的因素，即出现波动的各掘进参数，依次为盾壳摩擦力、掌子面压力、刀盘扭矩、盾尾注浆压力； aij和bij分别表示由于第i个参数出现第j级损失等级时地表沉降的下限与上限值，各经典域具体如式(3)—(7)。

(3)

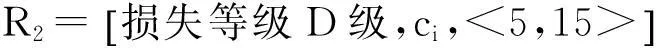
(4)

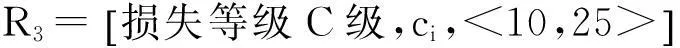
(5)

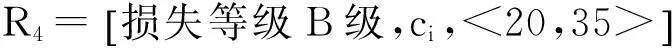
(6)

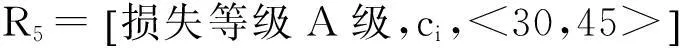
(7)

该盾构隧道风险损失的节域Rp，即每个因素ci波动产生地表沉降的全部的可能取值范围(其中包括由于因素ci波动引起其他因素波动导致的次生地表沉降等)，故

(8)

4.1.1.2确定待评物元——沉降计算值

由上述有限元参数化分析计算，现有待评价“产品”建国道站—天津站区间地表沉降损失p，当各参数出现波动时的地表最大沉降计算值vi(盾尾脱出后4d)分别为v1= 8.8mm、v2= 7.6mm、v3= 7.4mm、v4= 7.9mm，表示成待评价物元

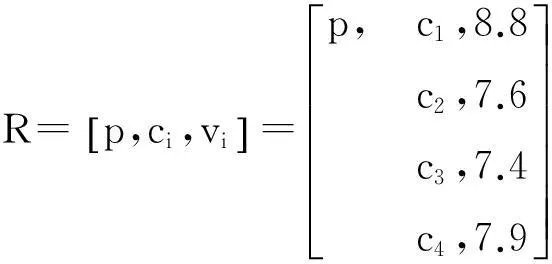
(9)

4.1.1.3确定参数权重

确定各参数影响权重的方法有很多，但大多都带有一定的主观性或太复杂不便于实际操作。本文采用简单关联函数法确定各参数影响的权重，该方法考虑的权重是相对具体沉降计算值与分级标准变化的，而不是绝对的，见式(10)，从而更具客观合理性。

(10)

根据本工程中vi∈Vip(节域)，故有

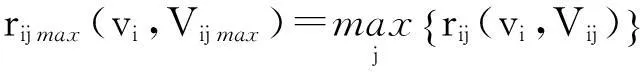
(11)

因为本工程中参数ci对应的数据落入的损失级别越大，该参数需被赋予的权重越大，故取式(12)。

(12)

故对盾构掘进中每个参数ci的权重

(13)

由式(12)—(13)计算得到，盾壳摩擦力的权重a1为0.313，掌子面压力的权重a2为0.270，刀盘扭矩的权重a3为0.135，盾尾注浆压力的权重a4为0.281。

4.1.1.4确定关于各风险损失等级的关联度

首先，根据式(1)定义，为了定量地描述每一个沉降计算值vi所属风险损失特征的程度及其变化，其关联函数见式(14)。

(14)

式中：

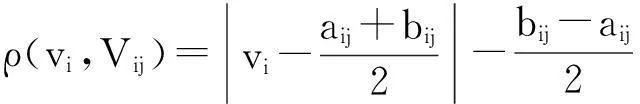
(15)

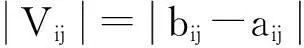
(16)

(17)

式(17)中aip、bip分别为节域中对应的上、下限，由式(14)—(17)计算本隧道施工地表沉降关于各风险损失等级的关联函数，然后根据式(18)计算隧道施工地表沉降风险损失等级j的关联度。

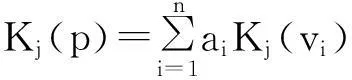
(18)

经计算可知，待评价隧道施工地表沉降的风险损失等级关联度依次为K1(p) = 0.196 7，K2(p)=0.303 3，K3(p)=-0.196 7，K4(p)=-0.598 3，K5(p)=-0.732 2。

4.1.1.5评估工程综合风险损失等级

该隧道地表沉降损失p的K2(p)最大，即j0= 2。根据规范[12]，建国道站—天津站区间隧道地表沉降的风险损失等级为“D级，需要考虑的”。为了进一步定量评估风险损失等级，定义式(19)。

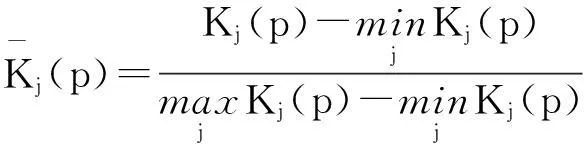
(19)

则有风险损失等级变量特征值

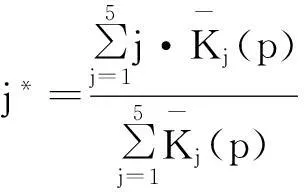
即建国道站—天津站区间盾构施工地表沉降的风险损失等级变量特征值j*= 1.95，表明该隧道施工4个参数都有出现波动的可能时，其风险损失等级属于E级偏向D级。

4.1.1.6评估单一参数风险损失等级

以上通过可拓法的应用可以得到工程综合风险损失等级，但在实际工程中为了更有针对性地指导施工，尽可能规避风险，也需要对单一参数(致险因子)的风险损失等级及其损失变量特征值进行计算评价。

当该盾构隧道施工中4个参数其中只有1个出现波动(n=1)，即待评价物元R=[ p，c1，v1](这里c1依次表示盾壳摩擦力、掌子面压力、刀盘扭矩、注浆压力其中1个评价参数)时，按照4.1.1.4节可以得到，地表沉降的单一参数风险损失等级依次为“需要考虑的”(K2(p) = 0.38)、“需要考虑的”(K2(p) =0.26)、“可忽略的”(K1(p) = 0.26)、“需要考虑的”(K2(p) = 0.29)。

可见，当只有1个参数出现波动时，刀盘扭矩对隧道施工地表沉降产生的风险损失等级最小。此外，根据式(3)—(7)，通过对单一参数盾壳摩擦力、掌子面压力、刀盘扭矩、注浆压力出现波动进行的风险损失等级评估，得到相应地表沉降上限值，即允许沉降值[δ]依次为15、15、10、15mm。

类似地，可以得到该隧道施工中4个参数其中只有1个出现波动(n=1)，即待评价物元R=[ p，c1，v1](c1依次表示盾壳摩擦力、掌子面压力、刀盘扭矩、注浆压力其中1个评价指标)时，地表沉降风险损失等级变量特征值j*依次为2.02、1.91、1.89、1.94。

4.1.2风险损失变量特征值评估

地表最大沉降增幅Δδmax，i与其参数相对波动区间长度ΔLi的比值Mi反映了地表沉降对各参数的敏感程度，即

(20)

式中: δmax，i和δmin，i分别为由第i个参数波动引起地表沉降值的上限与下限，Lmax，i和Lmin，i分别为第i个参数波动的上限与下限(监测值)，Ln，i为第i个参数的任一监测值，N为监测值总个数(N=157，如图3所示)。

比如，掘进过程中盾壳摩擦力Ff在6 000～15 600kN出现波动时(ΔL1=74.1%)，地表最大沉降变化幅值Δδmax，1约3.4mm(5.4～8.8mm)，比值M1=4.58为各参数中最大(见表2)，表示地表沉降最容易受到盾壳摩擦力Ff出现波动的影响。这也说明，一旦风险发生，盾壳摩擦力对风险损失影响的程度最大。于是定义各参数的重要性系数

。　(21)

建国道站—天津站区间盾构在施工过程中，尽管地表沉降均没有超过允许上限值[δ]，但最直接的风险损失就是占用了地表沉降的安全储备。综上，定义风险损失变量特征值

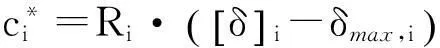
(22)

式中： [δ]i为第i个参数出现波动进行风险损失等级评估后而得到的地表允许沉降值，由4.1.1.6节得到[δ]i依次取值为15、15、10、15mm，从而计算各单一参数风险损失变量特征值(见表2)。结果表明该盾构隧道在施工过程中单一参数盾壳摩擦力、掌子面压力、刀盘扭矩、注浆压力对应的风险损失变量特征值c*依次为2.79、1.52、0.05、2.30。

4.2风险失效概率评估

第i个掘进参数出现波动后引起的地表最大沉降δmax，i越接近于地表允许沉降值[δ]i，风险事故发生的概率越高;当δmax，i= [δ]i时，意味着盾掘进参数一旦使地表沉降达到δmax，i，事故即发生[19]。故利用式(23)—(24)定义了风险失效概率的简化计算方法。

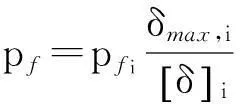
(23)

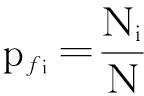
(24)

式中： [δ]i为通过对第i个参数出现波动进行的风险损失评估而得到的地表允许沉降值；Ni为第i个参数使地表沉降达到δmax，i的监测值个数；N为第i个参数的全部监测值个数。每个参数波动产生的风险失效概率计算结果见表3。

表3　风险失效概率

根据规范[12]，针对该待评价隧道，其盾壳摩擦力出现波动引起的失效概率为1.12%，相应的风险失效概率等级为2级“可能的”。类似地，掌子面压力、刀盘扭矩、注浆压力出现波动引起的失效概率等级依次为3级“偶尔的”、2级“可能的”、3级“偶尔的”。

当然，上述风险失效概率是基于所依托的实际工程资料进行统计分析得到的。在该工程中，采用了PLC控制系统后，由掌子面压力引起的风险失效概率得到了有效的控制(0.65%)。在此前提下，掘进参数的失效概率分析才得到上述结果。

4.3风险等级综合评估

4.3.1定性评估

根据规范[12]，可以得到盾构掘进参数定性的风险等级和综合风险等级，见表4。盾构掘进地表沉降的综合风险等级为Ⅲ级，其接受准则为“可接受的”，需要工程建设方引起重视，并采取合适的风险防范监控措施。控制方案与处置原则： 宜加强日常管理与监测；宜实施风险管理，可采取风险处理措施[12]。

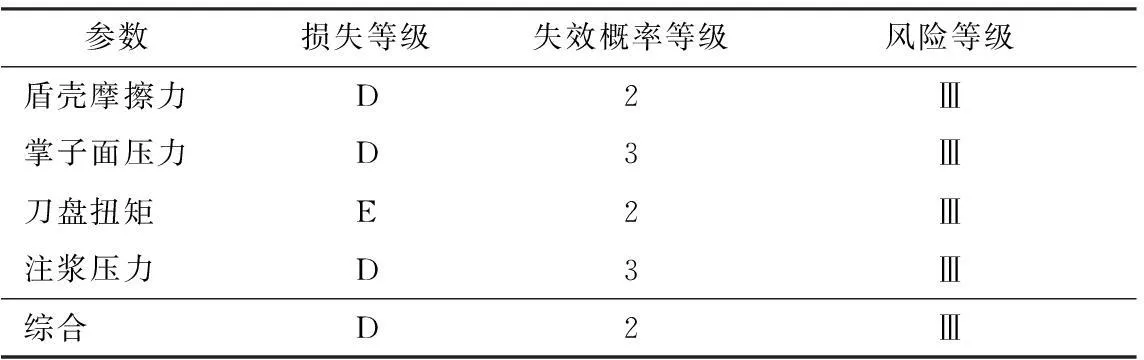
表4　风险等级综合评价

4.3.2定量评估

图7表明该盾构隧道在掘进施工时，风险值最大的致险因子是盾壳摩擦力(3.13%)，其余致险因子按风险值从大到小依次为盾尾注浆压力(1.54%)、土舱压力(0.98%)、刀盘正面扭矩(0.12%)。故在此区间后续下穿高速铁路的盾构在掘进过程中，宜针对风险值较大的盾壳摩擦力、注浆压力波动对地表沉降的潜在风险制定精细化控制措施。

5精细化控制

以上参数化分析以及风险评估是基于工程实例进行的，包括致险因子的排序均是基于工程计算结果分析而得到的。在该工程中，各项参数控制均在正常范围之内，特别是掌子面压力。在此前提下，参数化分析和风险分析才得到上述结论。如果各项参数均产生超过正常值范围的偏差，则情况要复杂得多。工程经验表明，当掘进施工参数偏差超过正常范围时，掌子面压力对沉降的影响也十分敏感。对这种更为复杂的情形，还需专门分析。故以下仅基于该工程的参数化分析及风险评估结果提出了相应的精细化控制技术措施。

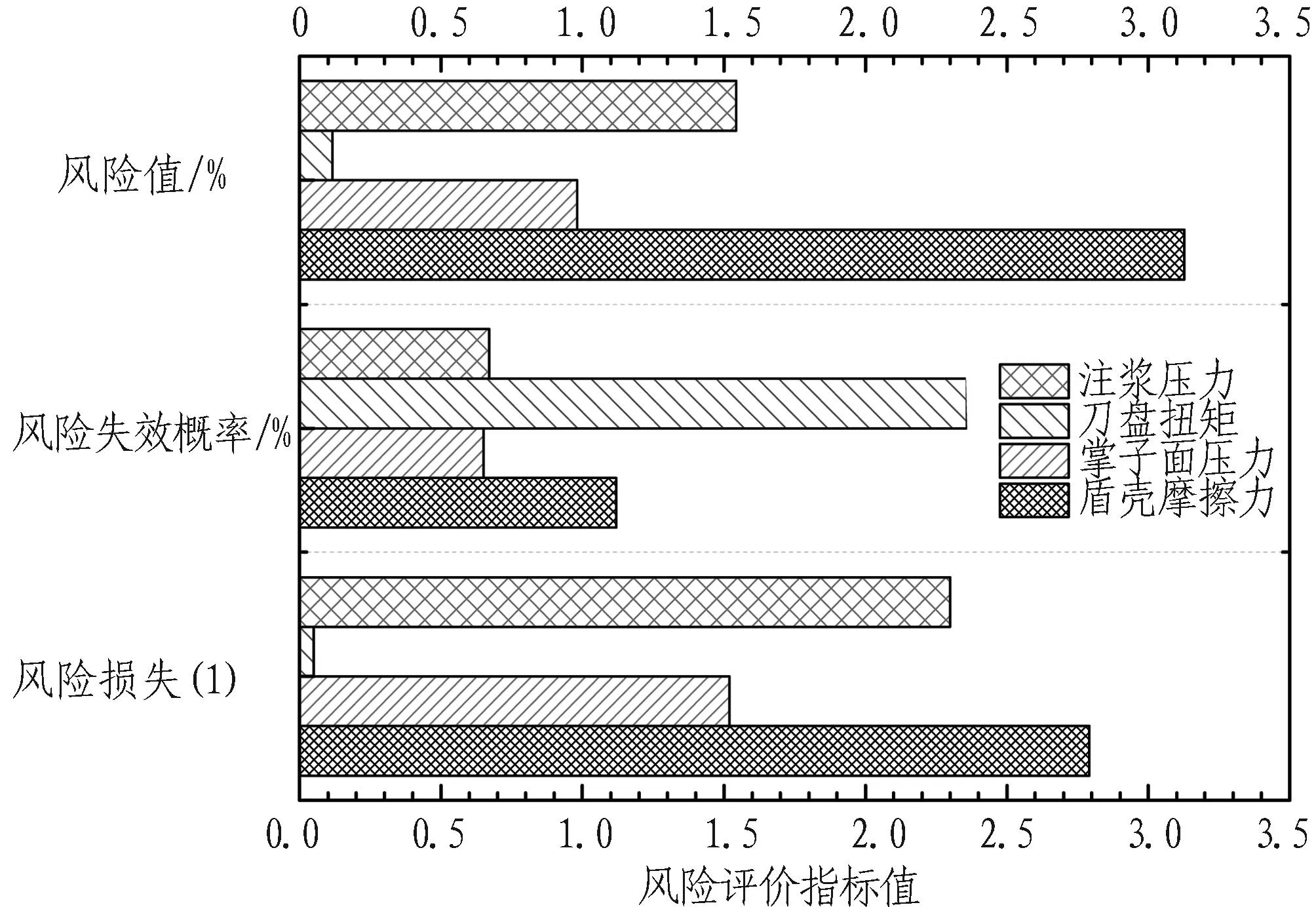
图7　各掘进参数的风险值比较

Fig. 7Comparison and contrast among every shield boring parameters in terms of value-at-risk

针对工程现场掘进地层存在变异性，如局部细砂等，容易造成盾壳摩擦力的波动，施工方采用如图8所示的通过中盾盾壳的径向孔注入膨润土润滑作为预防措施。此外，也采取适当提高注浆压力并辅以二次注浆作为地表沉降过大的控制措施。

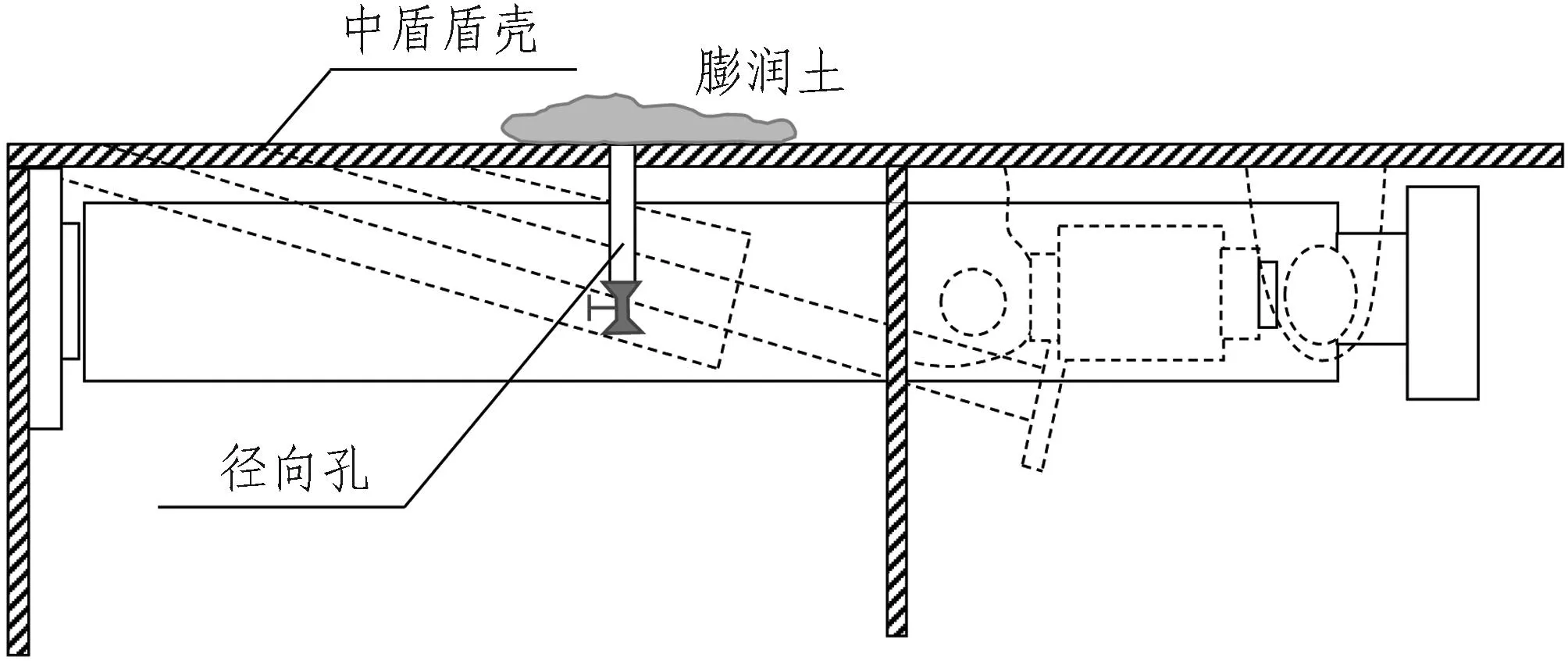
图8　径向孔注入膨润土

当采用风险控制措施后，该区间盾构继续掘进下穿高速铁路(254—276环)时地表沉降时程曲线如图9所示。

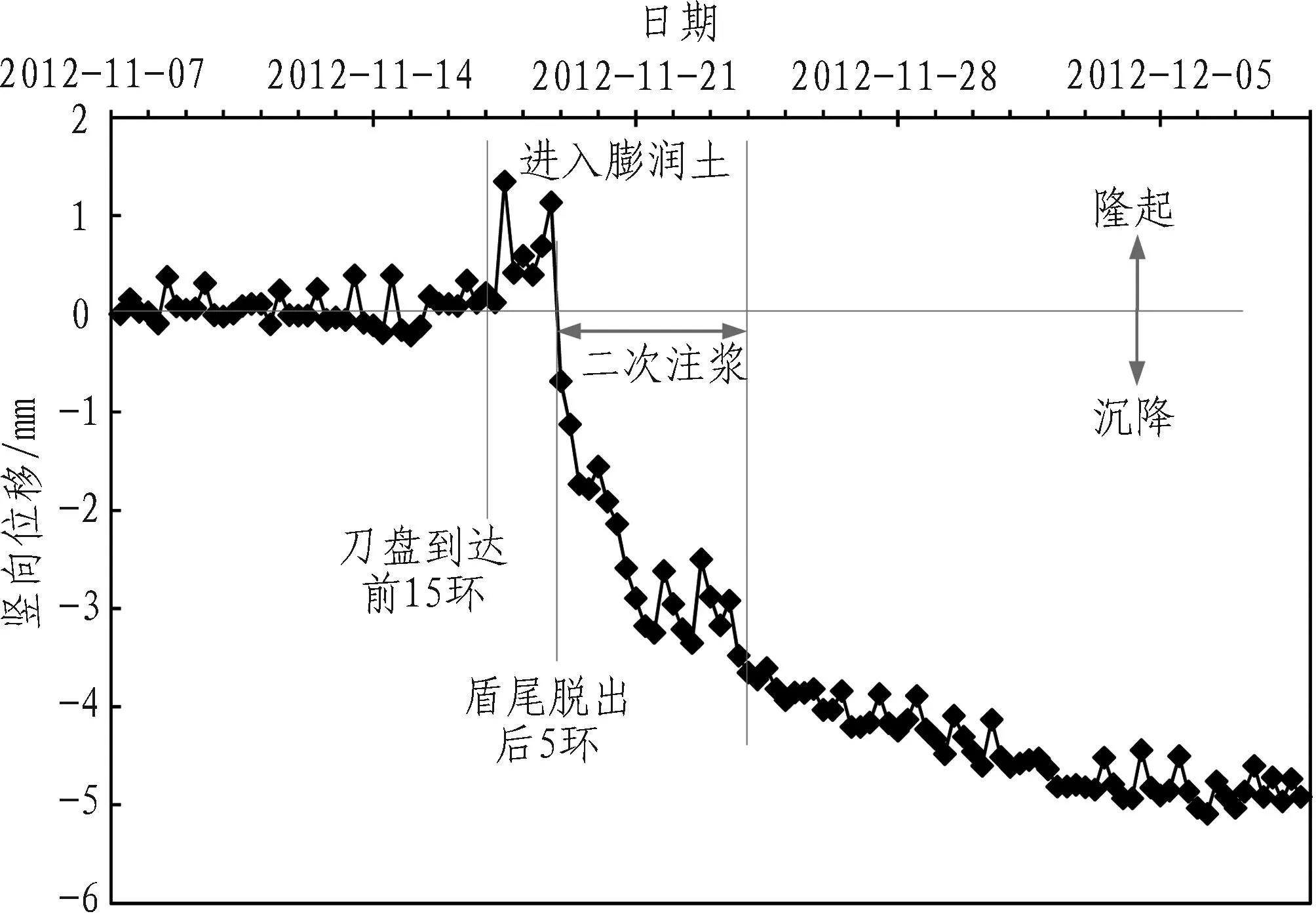
图9　下穿高速铁路地表沉降时程曲线

Fig. 9Time-history curve of ground surface settlement when shield boring underneath high-speed railway

由图9可知，从盾构刀盘到达前15环开始地表出现隆起，盾构通过阶段由于膨润土的注入大大降低了对周围土体的扰动，该阶段地表几乎没有出现沉降，直至盾尾脱出5环后地表才表现出明显的沉降趋势，施工方加强了对该部位的二次注浆。现该区域沉降逐渐趋于稳定，累计沉降5.1 mm，满足铁路部门的安全运输要求，也表明提出的风险控制措施是合理和有效的。

6结论与讨论

本文以天津地铁天津站—建国道站深埋盾构工程为依托，针对盾构掘进过程中盾壳摩擦力、刀盘扭矩、掌子面压力和注浆压力等盾构掘进参数对周围地表沉降影响进行了参数化计算分析，并基于地表沉降的计算结果进行了风险损失等级的可拓法风险评估，提出了风险值的定量评估方法与相应的精细化控制措施，得出如下结论。

1)基于参数化计算结果的可拓法可以用于合理、定量地评估盾构掘进地表沉降风险损失模型。基于盾构掘进参数的波动，该隧道的风险损失等级为“需要考虑的”，风险损失等级变量特征值j*= 1.95，表明该隧道施工4个参数都有出现波动时其风险损失等级属于E级偏向D级。盾构盾壳摩擦力、掌子面压力、刀盘扭矩、注浆压力之中只有1个出现波动时，地表沉降的风险损失变量特征值c*依次为2.79、1.52、0.05、2.30。

2)风险失效概率是通过对盾构掘进参数实测结果以及风险损失评估结果进行统计分析得到的。该隧道盾壳摩擦力和刀盘扭矩出现波动导致的风险失效概率等级为“可能的”，掌子面压力和注浆压力出现波动引起的失效概率等级为“偶尔的”。本文参数化分析以及风险评估是基于工程实例进行的，分析中采用的是成层土，这对结果会产生一定的不确定性。对不同单一土层的参数化分析尚需进一步研究。

3)以盾构掘进参数波动为致险因子，以地表沉降控制为目标进行定量风险分析，得出该区间致险因子按风险值从大到小依次为盾壳摩擦力、注浆压力、掌子面压力、刀盘扭矩。在该区间后续下穿高铁的盾构掘进过程中，针对风险值较大的盾壳摩擦力、注浆压力波动制定了精细化风险控制措施并取得了良好的效果，从而为类似工程中达到地表“毫米级”的变形控制要求提供了一定的参考与指导。

参考文献(References)：

[1]Kasper T, Meschke G. A numerical study of the effect of soil and grout material properties and cover depth in shield tunnelling [J]. Computers and Geotechnics, 2006, 33(4): 234-247.

[2]Kasper T, Meschke G. On the influence of face pressure, grouting pressure and TBM design in soft ground tunnelling [J]. Tunnelling and Underground Space Technology, 2006, 21(2): 160-171.

[3]沈建奇. 盾构掘进过程数值模拟方法研究及应用 [D]. 上海: 上海交通大学, 2009. (SHEN Jianqi. Research and application on numerical simulation method for shield tunneling [D]. Shanghai: Shanghai Jiaotong University, 2009. (in Chinese))

[4]Hasanpour R, Rostami J, Ünver B. 3D finite difference model for simulation of double shield TBM tunneling in squeezing grounds [J]. Tunnelling and Underground Space Technology, 2014, 40: 109-126.

[5]徐泽民, 郑刚, 韩庆华，等.地铁隧道下穿历史风貌建筑影响的实测与分析[J]. 岩土工程学报，2013，35(2)： 364-374. (XU Zemin, ZHENG Gang, HAN Qinghua,et al. Field monitoring and analysis of effects of Metro tunnels under historic buildings[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 364-374. (in Chinese))

[6]Eskesen S D, Tengborg P, Kampmann J, et al. Guidelines for tunnelling risk management: International tunnelling association, working group No. 2 [J]. Tunnelling and Underground Space Technology, 2004, 19(3): 217-237.

[7]黄宏伟, 曾明, 陈亮, 等. 基于风险数据库的盾构隧道施工风险管理软件: (TRM1.0)开发 [J]. 地下空间与工程学报, 2006, 2(1): 36-41. (HUANG Hongwei, ZENG Ming, CHEN Liang, et al. Risk management software: (TRM 1.0) based on risk database for shield [J]. Chinese Journal of Underground Space and Engineering, 2006, 2(1): 36-41. (in Chinese))

[8]黄宏伟. 隧道及地下工程建设中的风险管理研究进展 [J]. 地下空间与工程学报, 2006, 2(1): 13-20.(HUANG Hongwei. State-of-the-art construction of the research on risk management in tunnel and underground works [J]. Chinese Journal of Underground Space and Engineering, 2006, 2(1): 13-20.(in Chinese))

[9]安永林. 结合邻近结构物变形控制的隧道施工风险评估研究 [D]. 长沙： 中南大学, 2009. (AN Yonglin. Study on tunnel construction risk evaluation considering deformation standard of neighboring structures[D]. Changsha: Central South University, 2009. (in Chinese))

[10]彭立敏, 安永林, 张运良, 等. 可拓法识别勘测阶段隧道瓦斯突出的模型与实例[J]. 土木工程学报, 2008, 41(4): 81-85. (PENG Limin, AN Yonglin, ZHANG Yunliang, et al. Identification of gas burst in tunnel at the prospecting stage by using extension theory:A case study [J]. China Civil Engineering Journal, 2008, 41(4): 81-85. (in Chinese))

[11]安永林, 彭立敏, 吴波, 等. 隧道坍方突发性事件风险可拓法综合评估 [J]. 中南大学学报(自然科学版), 2011, 42(2): 514-520. (AN Yonglin, PENG Limin, WU Bo, et al. Comprehensive extension assessment on tunnel collapse risk [J]. Journal of Central South University(Science and Technology), 2011, 42(2): 514-520. (in Chinese))

[12]中华人民共和国住房和城乡建设部.城市轨道交通地下工程建设风险管理规范: GB 50652—2011[S].北京： 中国建筑工业出版社， 2011.(Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for risk management of underground works in urban rail transit: GB 50652—2011[S]. Beijing: China Architecture & Building Press,2011. (in Chinese))

[13]中华人民共和国住房和城乡建设部. 城市轨道交通工程监测技术规范: GB 50911—2013[S].北京： 中国建筑工业出版社，2014. (Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for monitoring measurement of urban rail transit engineering： GB 50911—2013[S]. Beijing: China Architecture & Building Press,2014. (in Chinese))

[14]蔡文. 可拓学概述 [J]. 系统工程理论与实践, 1998, 18(1): 77-84. (CAI Wen. Introduction of extenics [J]. System Engineering-Theory & Practice, 1998, 18(1): 77-84. (in Chinese))

[15]蔡文, 杨春燕, 林伟初. 可拓工程方法 [M]. 北京: 科学出版社,2000. (CAI Wen, YANG Chunyan, LIN Weichu. Extension engineering method[M]. Beijing: Science Press,2000. (in Chinese))

[16]ZHENG Gang, LU Ping, DIAO Yu. Advance speed-based parametric study of greenfield deformation induced by EPBM tunneling in soft ground [J]. Computers and Geotechnics, 2015, 65(1): 220-232.

[17]Komiya K, Soga K, Akagi H, et al.Finite element modelling of excavation and advancement processes of a shield tunnelling machine [J]. Soils and Foundations, 1999, 39(3): 37-52.

[18]Franzius J N, Potts D M, Burland J B. The influence of soil anisotropy and Ko on ground surface movements resulting from tunnel excavation [J]. Geotechnique, 2005, 55(3): 189-199.

[19]郑刚, 路平, 曹剑然. 基于盾构机掘进参数对地表沉降影响敏感度的风险分析 [J]. 岩石力学与工程学报, 2015, 34(增刊1): 3604-3611. (ZHENG Gang, LU Ping, CAO Jianran. Risk analysis based on the parameters sensitivity analysis for ground settlement induced by shield tunneling [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 3604-3611. (in Chinese))

Study on Risk Assessment and Fined Control of Influence of Shield Tunneling on Ground Surface Settlement: A Case Study on Tianjin Metro

LU Ping1, 2, ZHENG Gang1, 2, ZHANG Wenjun1, 2, LEI Huayang1, 2

(1.SchoolofCivilEngineering,TianjinUniversity,Tianjin300072,China；2.KeyLaboratoryofCoastCivilStructureSafetyofMinistryofEducation,TianjinUniversity,Tianjin300072,China)

Abstract:The requirements on ground surface deformation in the construction of Metro in urban areas are strict. The influence of shield boring parameters of Tianjin Station Station-Jianguodao Station section of Tianjin Metro, such as shield friction, cutterhead torque, working face pressure and grouting pressure, on ground surface settlement is numerically simulated. The risk assessment based on extension method is made on risk failure grade of calculation results of ground surface settlement under different shield boring parameters. The risk failure rate is obtained based on analyzing on the assessment results of risk failure and measured data of shield boring parameters; and then the risk value of every risk factor is calculated and relative fined control technology is proposed. The results show that: 1) The order of risk factors of the test section based on value-at-risk are shield friction, grouting pressure, working face pressure and cutterhead torque. 2) The final ground surface settlement of 5.1 mm can meet the requirements by using fined control technologies.

Keywords:Tianjin Metro; shield tunnel; parametric analysis;ground surface settlement; extension method; risk assessment

中图分类号：U 45

文献标志码：A

文章编号：1672-741X(2016)02-0170-09

DOI:10.3973/j.issn.1672-741X.2016.02.008

作者简介：第一 路平(1986—)，男，河北唐山人，2015年毕业于天津大学，岩土工程专业，博士，讲师，主要从事岩土工程以及地下工程的科研与教学工作。E-mail： paul19866612@126.com。

基金项目：国家重点基础研究发展计划(973计划)资助项目(2010CB732106)

收稿日期：2015-08-20; 修回日期: 2015-09-20