基于稀疏矩阵变换降维的高光谱图像目标探测算法

周　鑫　谭毅华

(华中科技大学自动化学院　武汉　430074)



基于稀疏矩阵变换降维的高光谱图像目标探测算法

周鑫谭毅华

(华中科技大学自动化学院武汉430074)

摘要目标探测是高光谱遥感中的一个非常重要的问题,针对高光谱图像数据量大和维度高的问题,提出了基于稀疏矩阵变换(Sparse Matrix Transform,SMT)降维的探测算法。首先基于协方差的约束最大似然估计,对高光谱数据进行稀疏矩阵变换,对降低维度后的数据结合经典的点目标检测算法,实现高光谱数据中的目标探测。在真实测试数据上,对算法进行了测试,可达到提高检测速度和检测效率的目的。

关键词高光谱图像; 目标探测; 稀疏矩阵变换(SMT); 协方差; 最大似然估计

Hyperspectral Target Detection Algorithms Based on Sparse Matrix Transform

ZHOU XinTAN Yihua

(College of Automation, Huazhong University of Science and Technology, Wuhan430074)

AbstractTarget detection is very important issue in hyperspecrtral remote sensing, aiming at high dimention and huge amount of data of hyperspectral image, algorithms based on sparse matrix transform(SMT) are proposed. SMT which based on maximum likelihood estimation of covariance is used to transform the high-dimention data to low-dimention data, combined with classic point taget detection algorithms to achive good detection results. The algorithms are detected on real data set, and prove to be more efficient.

Key Wordshyperspectral image, target detection, sparse matrix transform(SMT), covariance, maximum likelihood estimation

Class NumberTP391

1引言

高光谱遥感是指通过搭载在飞机或卫星上的成像光谱仪同时获取一定空间区域内地面物体的图像和高分辨率光谱数据。由于高光谱遥感图像可以提供区分不同物质的诊断性光谱特征信息,目标探测成为高光谱遥感图像处理中一个引人关注的重要问题。当目标的光谱特征已知时,探测算法需要将待探测的遥感图像中目标地物与其他地物进行区分,判断目标在各个像素内的存在性[1];当目标和背景等先验信息未知时,则需要通过异常探测方法来获取目标的信息[2~3]。

由于高光谱图像光谱分辨率高、波段数很多,导致了信息的冗余和数据处理复杂性的增加,高光谱特征降维成为了解决维数灾难的常用方法,在高光谱图像处理中具有十分重要的作用[4]。主成分分析(Principal Components Analysis,PCA)[5]是一种最常用的线性降维方法。它的主要目标是通过线性变换寻找一组最优的单位正交向量基,并用它们的线性组合来重构原样本,以使重建后的样本和原样本的误差最小。但是PCA同时具有图像数值变化影响明显和信噪比不一定随着主成分编号的增加而降低等缺陷,单纯地采用传统的PCA等降维方法有时并不一定是最优选择。本文基于稀疏矩阵变换(SMT)降维[6~8],得到了较好的实验效果。

2基于稀疏矩阵变换的高光谱数据降维

在遥感数据处理的诸多问题例如数据降维中都需要用到协方差估计的方法,协方差是一个关键的统计量,特别是对于高维数据而言。主成分分析(PCA)是最经典的降维方法,它需要对协方差矩阵的精确估计。

对于高光谱图像的检测特别是小目标的检测中,样本数量很容易小于图像的波段数目,在这种情况下就会出现样本协方差相对于实际协方差的过度拟合现象,从而导致探测性能降低。以下本文介绍地基于最大似然的稀疏矩阵变换(SMT),能很好地解决过度拟合问题。SMT将投影变换表示成一个连续的吉文斯旋转的过程,这样投影算子的计算十分高效,因此它具有比PCA降维更加快速的优点。

2.1协方差的最大似然估计

假设原始图像数据为X,我们可以用向量X=[x1,x2,…,xn]表示,任意列向量xi维数为p,图像的总像素数为n,则我们可以用P*q维降维算子Eq乘以X得到降维后的q维数据Y。

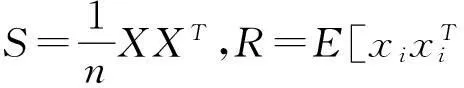
假设X的列是均值为0的独立同分布高斯随机向量,则X的似然估计为

(1)

取对数:

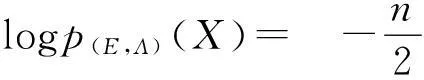
(2)

为求其最大似然估计,即只要满足:

(3)

(4)

Ω是符合正交变换的集合。

2.2基于ML特征向量估计的SMT模型

通过约束Ω,对E的ML估计效果可以得到增强,可以建立一个模型来有效地对E进行ML估计。建模方法关键点是使Ω尽可能小但是却不失数据的准确性。

用K阶的稀疏正交矩阵变换来表示E:

(5)

其中每一个稀疏矩阵Gk都是对一对坐标(ik,jk)进行吉文斯旋转:

Gk=I+Θ(ik,jk,θk)

(6)

其中Θ(i,j,θ)的定义为

(7)

那么当k=0到K-1过程中,即满足:

(8)

(9)

这样要首先确定两个坐标ik和jk:

(10)

进一步得到角度:

(11)

这样得到每一步的G*,就得到了E的ML估计:

(12)

图1SMT降维过程

3目标探测

基于稀疏矩阵变换降维的方法,先利用SMT变换得到低维影像,再将低维影像输入各探测器。这样能够避免求解虚拟维数、高维矩阵逆矩阵,减少噪声的干扰,提高探测的可靠性和速度。图2为目标探测的流程图。

图2　目标探测流程图

4实验结果与讨论

我们选取的图像为罗切斯特理工大学提供的一幅HyMap图像[9],图像地点为美国蒙大拿州Cook市,图像大小为280×800,波段数为126个,跨度从可见光至近红外(VNIR)到短波红外(SWIR)。图像的地面空间分辨率为3m,光谱分辨率为14nm。图像数据中包含blind-test数据及self-test数据,blind-test数据未给出目标的光谱曲线而self-test数据给出了光谱曲线,我们选用self-test作为实验数据。

self-test数据中包含四个织物目标和三个汽车目标,为了测试算法的性能,我们采取了植入目标的方法。以汽车目标中的V3为探测目标,在原图的一块大小为200×550的子图像中按照线性的方法等间距地植入24个目标,

xp=(1-p)x+pt

(13)

式中x为背景的光谱数据,本次实验中随机地选择100个背景数据按照0.01的比例混合而成,t为目标的光谱数据,选用V3的光谱数据,P为目标植入分数即目标所占的比例。按照这样的线性植入方法,24个目标的p值按照从左至右、从上至下以等差数列递增,依次为0.04,0.08,…,0.96。通过图6的最终探测结果三维图可以看出随着目标植入比例的不同,与背景的差异也不同,植入比例越高的像素其探测效果越好。

图4　目标V3实拍

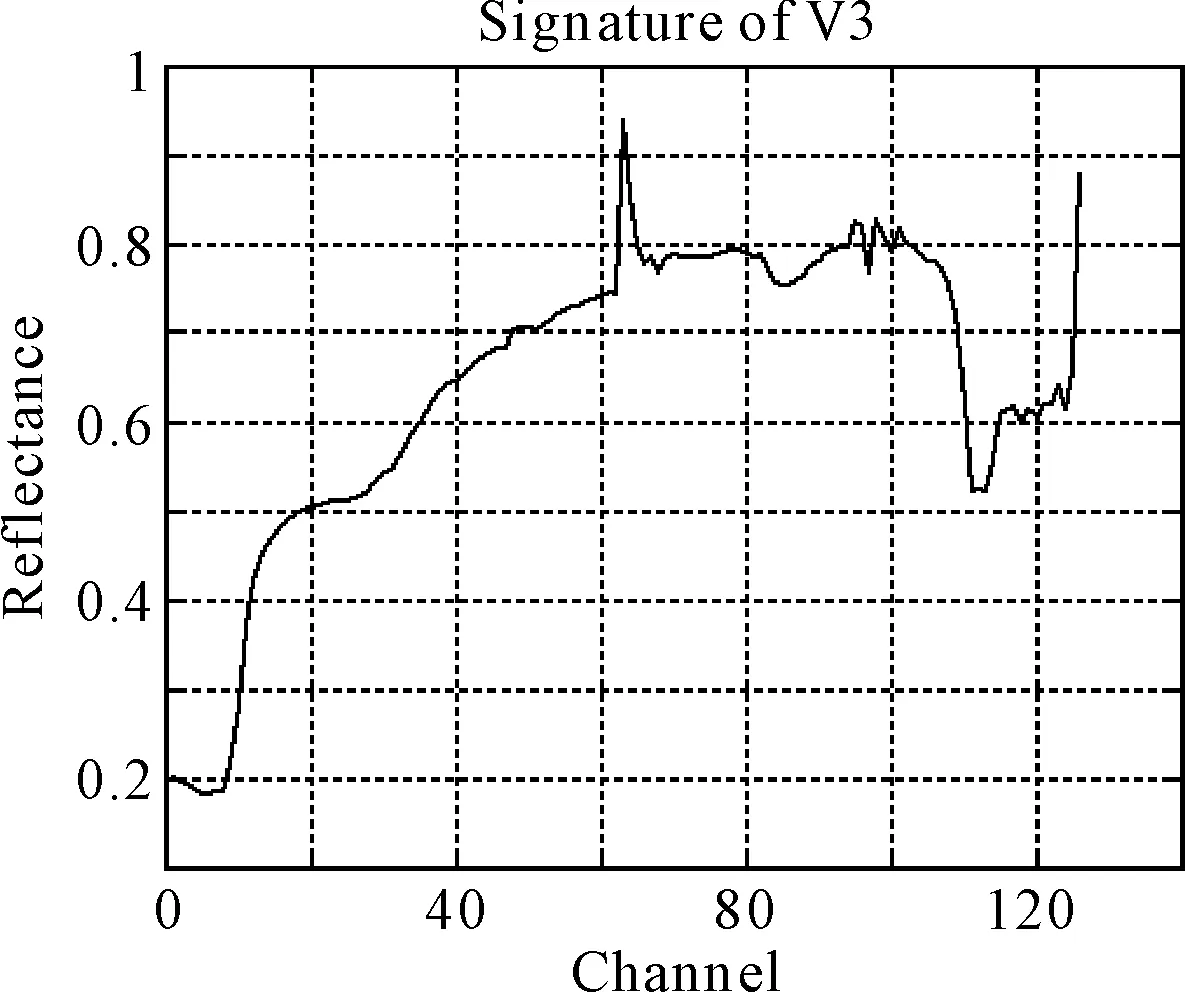
图5　V3的光谱曲线

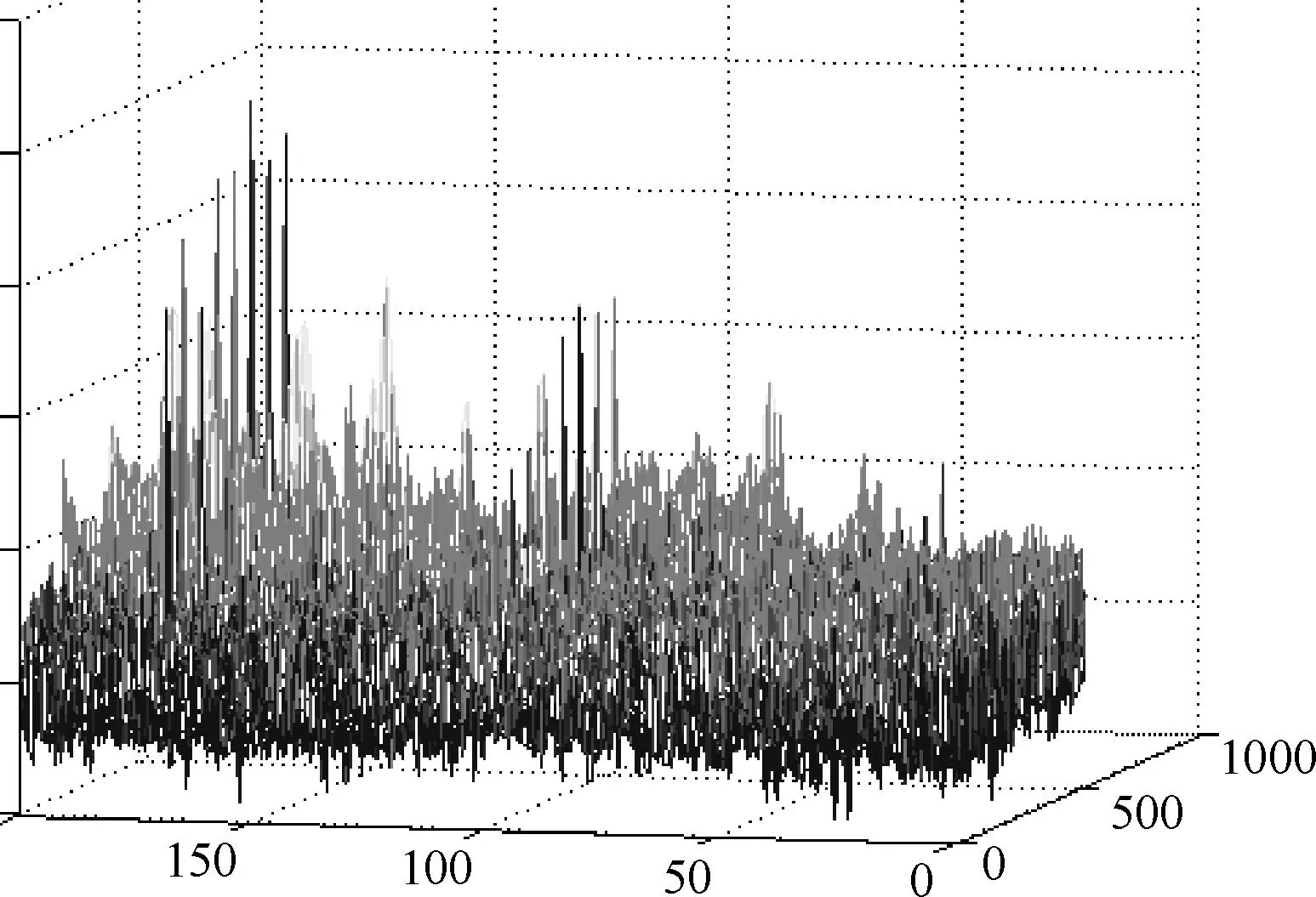
图6　植入目标后探测三维曲线

根据图2的方法,分别采用SMT降维和PCA降维对图像进行处理,然后取10维数据进行目标探测,目标探测算法我们选用了约束能量最小化方法(CEM)[10]、匹配滤波算法(MF)、自适应余弦一致性评估器(ACE)[11]和正则化的约束能量最小化方法(Re-CEM)[12]。为了测试随机噪声对结果的影响,加入了15分贝的高斯白噪声,目标探测算法的性能可以用ROC(receiver operating characteristic)曲线来作评价,图7~10为各算法在经过SMT降维和PCA降维后的ROC曲线比较。

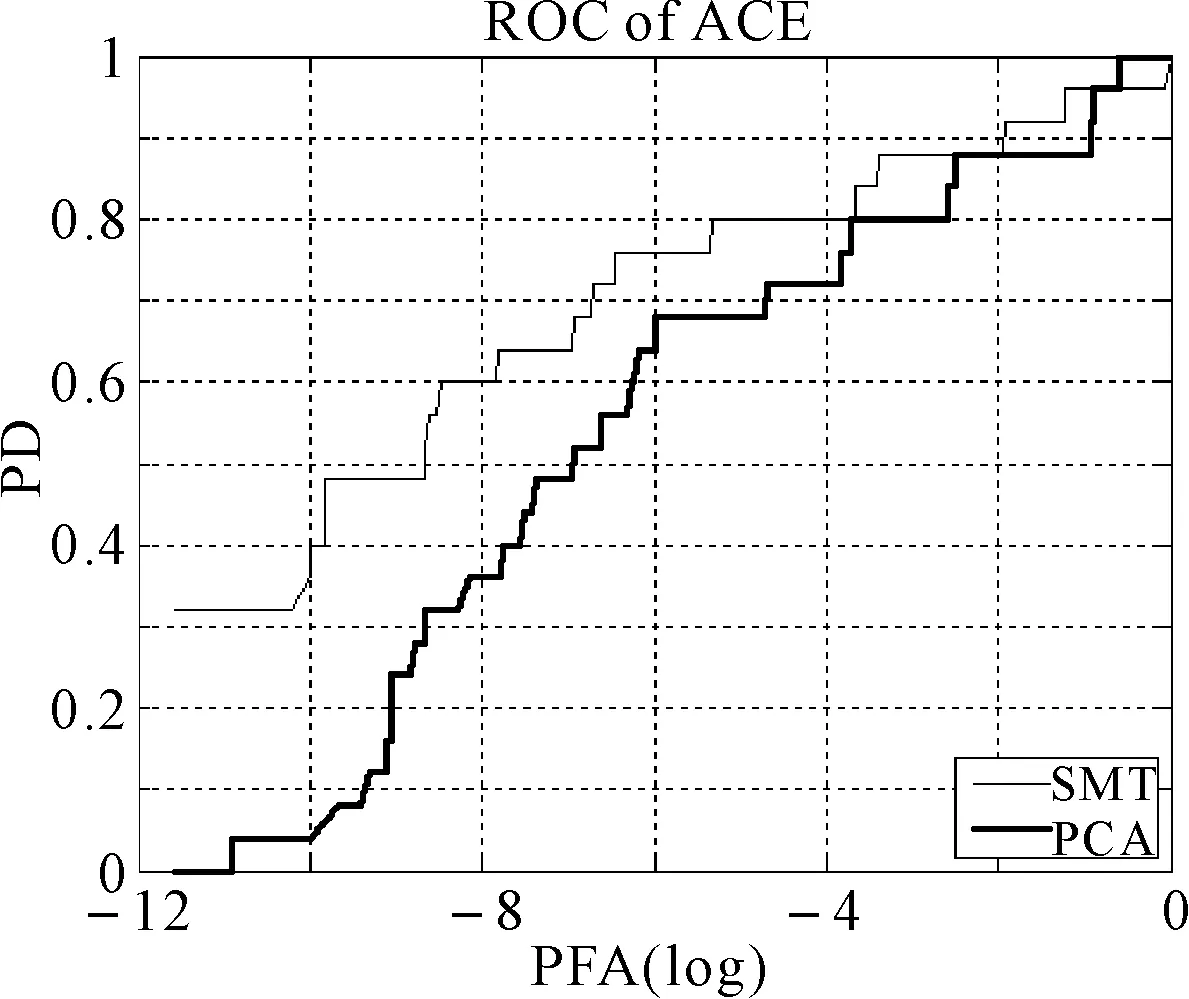
图7　两种降维方法在ACE算法下的ROC曲线比较

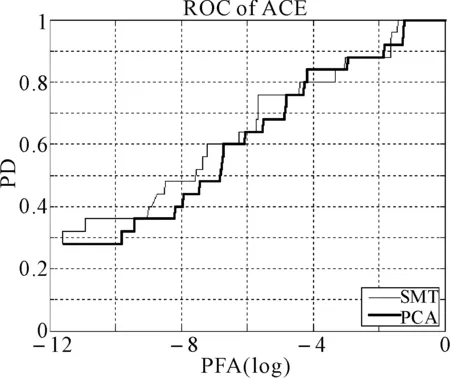
图8　两种降维方法在CEM算法下的ROC曲线比较

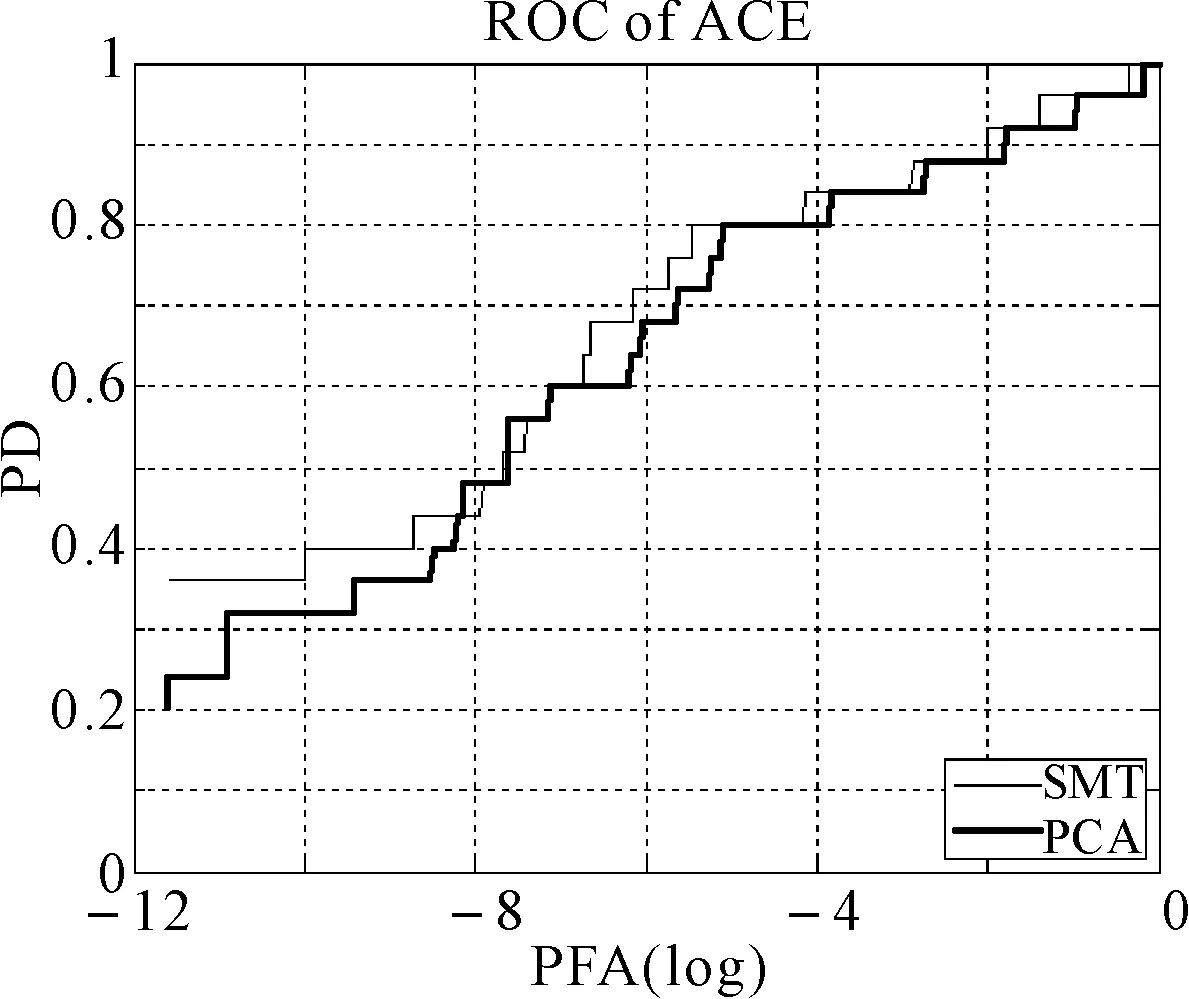
图9　两种降维方法在MF算法下的ROC曲线比较

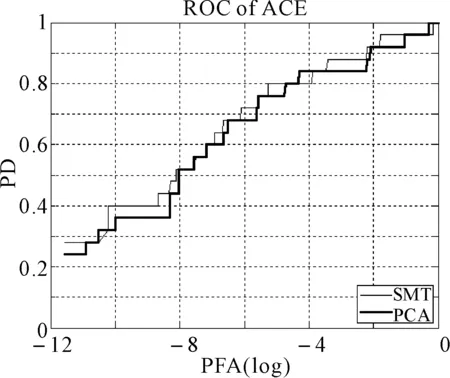
图10　两种降维方法在Re-CEM算法下的ROC曲线比较

由实验所得的ROC曲线可以看出,在经过不同的探测算法后,SMT降维的效果比PCA降维的效果要好,在ACE算法下的表现尤为明显。

从表1中可以看出,在时间上SMT比PCA用时短,这说明SMT在运算速度上更快,比PCA更加高效。

表1　两种降维方法速度比较

5结语

本文主要针对稀疏矩阵变换(SMT)降维方法展开,提出了一种基于最大似然协方差估计的SMT模型,由于采用了吉文斯旋转的过程,它比传统的主成分分析(PCA)更加快速高效。实验结果表明,在植入目标的条件下,SMT降维方法的表现比PCA降维更加理想。

参 考 文 献

[1] 杜博.高光谱遥感影像亚像元小目标探测研究[D].武汉:武汉大学,2010.

DU Bo. Study on Small Object Detection in Hyperspectral Remote Sensing Images[D]. Wuhan: Wuhan University,2010.

[2] Goetz A F H, Vane G, Solomon J E, et al. Imaging Spectrometry for Earth Remote Sending[J]. Science,1985,228(4704):1147-1153.

[3] Bioucas-Dias J M, Plaza A, Camps-Valls G, et al. Hyperspectral remote sensing data analysis and future challenges[J]. Geoscience and Remote Sensing Magazine, IEEE,2013,1(2):6-36.

[4] Chang C I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification[M]. New York: Plenum,2003.

[5] Jolliffe L. T. Principal Component Analysis[M]. 2nd ed. New York: Springer,2002.

[6] Cao G, Bouman C. Covariance estimation for high dimensional data vectors using the sparse matrix transform[C]//Advances in neural information processing systems,2009:225-232.

[7] Cao G, Bouman C A, Theiler J. Weak signal detection in hyperspectral imagery using sparse matrix transform(SMT) covariance estimation[C]//Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, 2009. WHISPERS’09. First Workshop on. IEEE,2009:1-4.

[8] Cao G, Bouman C A, Webb K J. Noniterative map reconstruction using sparse matrix representations[J]. Image Processing, IEEE Transactions on,2009,18(9):2085-2099.

[9] Rissanen J. Modeling by shortest data description[J]. Automatica,1978,14(5):465-471.

[10] Schwarz G. Estimating the dimension of a model[J]. The Annals of Statistics,1978,6(2):461-464.

[11] Kraut S, Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J]. Signal Processing, IEEE Transactions on,1999,47(9):2538-2541.

[12] Zhang Y, Du B, Zhang L. Regularization framework for target detection in hyperspectral imagery[J]. Geoscience and Remote Sensing Letters, IEEE,2014,11(1):313-317.

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.01.035

作者简介:周鑫,男,硕士研究生,研究方向:高光谱遥感。

收稿日期:2015年7月8日,修回日期:2015年8月12日