采用粒子滤波的雷达波束方位指向估计*

陆珊珊，王　伟，王国玉

(1. 国防科技大学 电子科学与工程学院， 湖南 长沙　410073；

2.国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙　410073)



采用粒子滤波的雷达波束方位指向估计*

陆珊珊1,2，王伟1，王国玉1

(1. 国防科技大学 电子科学与工程学院， 湖南 长沙410073；

2.国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙410073)

摘要：传统方位指向估计方法难以适应天线扫描速度变化的情形，为此建立波束方位指向估计的状态空间模型，并引入粒子滤波技术对状态变量进行估计。粒子滤波是非线性和非高斯情形下进行状态估计的强有力算法，采用粒子滤波的雷达波束方位指向估计算法具有良好的性能，能够适应天线扫描速度变化的情形。仿真实验验证了所提算法的适用性和有效性。

关键词：雷达侦察；扫描分析；波束方位指向；粒子滤波

雷达扫描分析是识别其工作模式的重要依据，同时也是精确电子干扰的基础，在雷达侦察和对抗领域具有重要的意义。扫描分析主要包括扫描方式识别、天线类型以及天线波束指向分析等[1-4]。对空情报雷达和目标指示雷达常用的扫描模式是利用方位窄/俯仰宽的扇形波束在方位向进行圆周扫描。对于该类雷达系统，波束方位指向估计是扫描分析的主要内容。鉴于机械扫描雷达是雷达系统的重要组成部分，主要考虑方位向机械扫描的雷达系统。

针对上述类型的雷达系统，传统的波束方位指向估计方法通过多次测量两次主波束照射的时间差来估计天线的扫描周期，进而结合主波束扫过接收机的时刻对其方位指向进行预测与估计[5-6]。该方法仅利用主波束扫描过接收机的时间信息，在波束方位指向估计方面较为被动。当天线扫描速度改变时，通常需要数个扫描周期才能重新适应新的扫描速度，难以适应快速多变的现代电子战环境。

为解决上述问题，陆珊珊等提出了一种基于粒子滤波的雷达波束方位指向估计算法。该算法以雷达波束方位角及其扫描速度为状态变量建立系统状态空间模型，随后引入粒子滤波技术对该非线性模型进行求解。粒子滤波是基于贝叶斯理论和统计抽样的信号处理方法，适用于非线性非高斯环境下的参数估计问题[7-12]。基于粒子滤波的方位指向估计算法综合利用了状态方程和观测方程的信息，能够实时估计雷达波束方位角及其扫描速度，具有适应扫描速度变化的能力，拥有较好的估计性能。

1系统模型

考虑方位向的波束扫描，在波束方位指向估计模型中，以对方雷达所在位置为坐标原点，以雷达与侦察接收机连线为横轴建立坐标系统。模型采用离散的时间系统，抽样时间间隔记为T，抽样时刻统一使用k表示。记k时刻雷达主波束方位角为θk，其对应扫描速度为wk，图1给出了系统模型示意图。

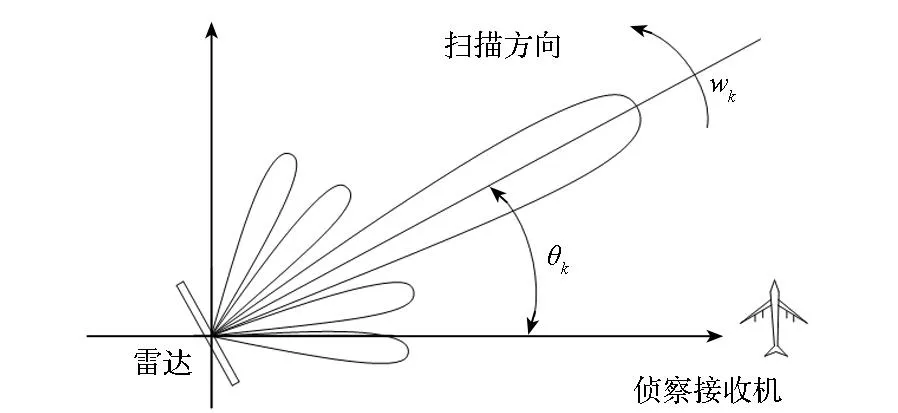
图1　系统模型示意图Fig.1　Schematic diagram of system model

由于系统的惯性作用，机械扫描雷达的波束方位角及其扫描速度通常是渐进改变的。相邻时刻波束方位角的关系为θk+1=θk+Twk，扫描速度关系为wk+1=wk+vk，其中vk为该时刻扫描速度抖动。取xk=[θk,wk]Τ为模型状态变量，则系统状态方程为：

xk+1=Axk+vk

(1)

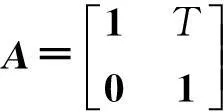
对于在方位向进行圆周扫描的雷达系统，接收信号的幅值随方位角而变化，当波束指向侦察机时达到最大。如果接收信号幅值在一个很大的动态范围内被精确地记录，则经过分析可得到方位向的天线方向图[1]。设以方位角为变量的方向图增益函数为G(θk)，取信号幅值为观测输出，则系统观测方程为：

(2)

2采用粒子滤波的估计算法

2.1算法描述

估计算法在给定观测数据y1:k的情形下，递归估计当前的状态变量xk。为此需要构造后验概率密度p(xk|y1:k)，由于系统观测方程的非线性，难以得到该后验概率的解析解。粒子滤波是解决该类问题的数值方法，利用加权样本集的演化来递推目标状态的后验概率密度，适用于非线性非高斯情形下的估计问题。

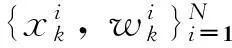
(3)

直接从后验分布得到样本较为困难，为此引入重要密度函数q(·)，此时重要性权值[10]为：

(4)

(5)

假定天线扫描速度抖动向量vk服从高斯分布，则根据系统状态方程可得：

(6)

由于量测噪声nk满足高斯分布，根据系统观测方程，结合信号检测理论可得：

(7)

其中，A=(PR0G(θk))1/2，I0(·)为第一类零阶修正贝塞尔函数。式(7)的表达式较为复杂，实际应用中可采用其近似形式。

迭代更新重要权值和响应样本即得到序列重要性采样类滤波算法。然而该类算法在多次迭代之后会出现退化现象，即权重集中到少数样本点上，此时样本集不足以描述待求后验分布。为解决该问题，可以通过重采样方法对样本集进行修正，其基本思想是增加权重较大样本的数目并减小权重较小样本的数目[11]。

综合上文分析，可得基于粒子滤波的雷达波束方位指向估计算法的主要步骤：

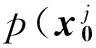
4)估计输出得到新的样本集和相应权值后，可以通过线性最小均方误差准则对状态变量xk进行估计，估计公式为：

(8)

其中，xk=[θk,wk]Τ的两个元素分别对应波束方位指向以及其扫描速度。

重复步骤2至步骤4即可实现雷达波束方位指向的实时估计。基于粒子滤波的估计算法综合利用了状态方程的信息以及观测方程中接收信号的幅值信息，能够及时跟踪扫描参数的变化，具有较好的估计性能。

2.2算法可行性分析

上述算法利用了副瓣信号的幅值信息，该信息的可用性取决于其信噪比。为分析信号信噪比，首先计算天线增益为0 dBi时的信噪比。忽略信号和噪声的同步放大过程，记接收信号功率为Pr，噪声功率为Pn，为方便起见采用dB形式的表达式，则根据雷达方程可得：

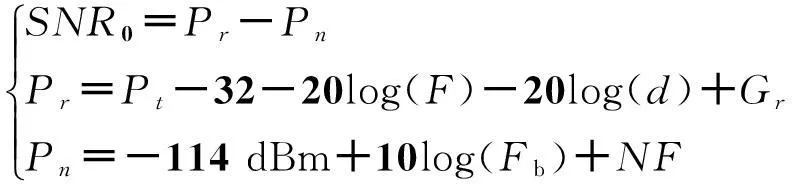
(9)

其中：Pt为雷达发射机功率，dBmW；F为发射信号频率，MHz；d为雷达与侦察接收机的距离，km；Gr为接收天线增益，dB；Fb为接收机带宽，MHz；NF为噪声系数，dB。

为直观表示设定情形下SNR0的取值，假定雷达发射功率Pt为100 kW，发射频率F为3 GHz，接收机带宽Fb为100 MHz，噪声系数NF为10 dB，图2给出了接收天线增益Gr为10 dB和20 dB时SNR0随距离d的变化曲线。

图2　SNR0随距离的变化曲线 Fig.2　Sketch of SNR0versus distance

现代雷达副瓣增益一般在-10 dBi以下，此时实际信噪比应在SNR0的基础上减去该副瓣增益。算法可行性与要求的估计性能有关，估计性能与副瓣信号信噪比有关，假定信号信噪比为10 dB时算法具有较好的估计性能。由此考虑适当的余量，则SNR0为30 dB时能够满足算法可行性的要求。由图2可知设定情形下SNR0的取值能够在较大范围内满足该要求。

3仿真分析

仿真中雷达天线设置为等间距的线阵，天线主波束始终指向阵列法线方向，通过机械装置完成空间扫描。阵元个数设为32，阵元间距为半波长，采用泰勒照射函数对阵元进行加权，靠近主瓣的5个副瓣设置为低于主瓣40 dB。图3给出了基于上述参数的雷达天线方向图。

图3　仿真天线方向图Fig.3　Antenna pattern in simulation

由图3可知，发射天线最外侧副瓣峰值位置约为-75°，该值为初始化过程中的起始值。天线初始扫描速度为36°/s，至方位角为-30°时开始均匀加速，至方位角为30°时加速至54°/s，随后维持该速度至扫描结束。仿真中粒子个数设置为200，为分析算法在不同信噪比下的估计性能，SNR0值设置为20 dB，30 dB和40 dB三种情形。图4给出了100次独立实验时波束方位角估计值与实际值的均方根误差曲线。

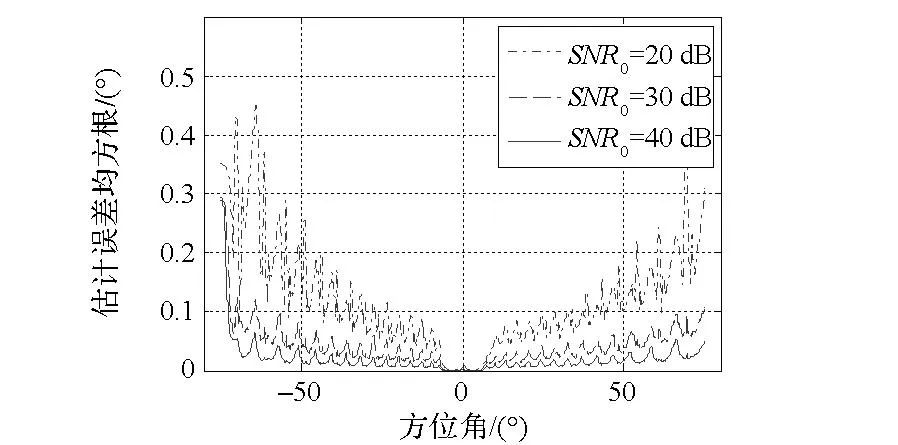
图4　估计算法均方根误差曲线 Fig.4　Mean-square-root errors curve of estimate algorithm

由图4可以看出，当SNR0取值为30 dB和40 dB时，算法稳定后均方根误差的最大值分别约为0.12°和0.06°，表明算法在较大信噪比情形下具有较好的估计性能。前文算法可行性分析给出了SNR0为30 dB时具有较好性能的经验型结论，该结论可由上述仿真结果证实。SNR0取值为20 dB时，算法需要较长时间才能稳定且误差较大，从而可以确定20 dB为本次实验最低工作SNR0。天线最外侧副瓣峰值增益约为-15 dBi，由此可知算法要求的最低副瓣信号信噪比约为5 dB。需要指出的是，均方根误差随方位角改变并非单调的变化，而是呈现出一种“梳子”的形状，这是由于当接收机位于天线副瓣的峰顶及零点处时估计误差总是较大的缘故。

图5给出了扫描速度的平均估计值。由图5可知在SNR0取值为30 dB和40 dB时，算法能够较为准确地估计天线扫描速度。在SNR0取值为20 dB时，扫描速度估计性能相对较差，但仍能准确给出扫描速度的变化情况。

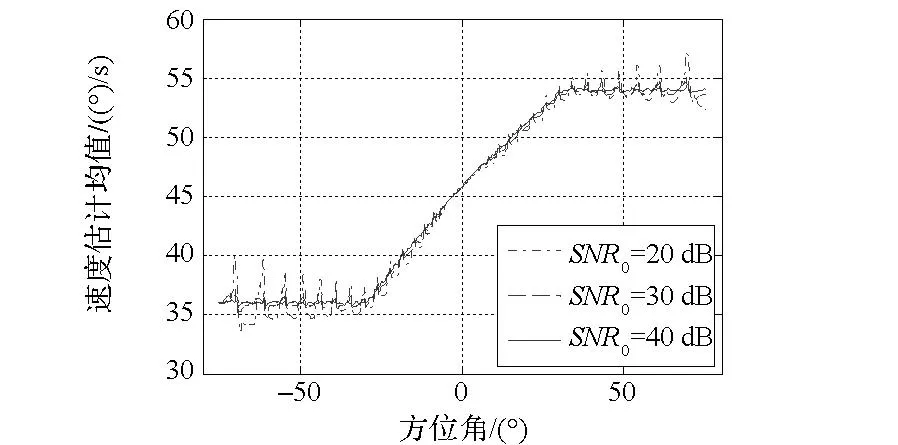
图5　扫描速度估计曲线 Fig.5　Scanning speed estimation curve

4结论

雷达波束方位指向估计在雷达对抗领域具有较为重要的意义。提出一种基于粒子滤波的估计算法，克服了传统方法仅能适应匀速扫描的不足。仿真结果表明，所提算法能适应扫描速度变化的雷达系统，有较高的估计精度。该算法为雷达波束方位指向估计提供了新的思路，在雷达对抗领域具有较好的应用前景。

参考文献(References)

[1]Wiley R G. ELINT: the interception and analysis of radar signals [M]. Norwood,USA: Artech House, 2006.

[2]Barshan B, Eravci B. Automatic radar antenna scan type recognition in electronic warfare [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 2908-2931.

[3]Kim Y H, Song K H, Han J W, et al. Radar scan pattern analysis for reduction of false identification in electronic warfare support systems [J]. IET Radar Sonar Navigation, 2014, 8(7): 719-728.

[4]李程, 王伟, 施龙飞, 等. 雷达天线扫描方式的自动识别方法[J]. 国防科技大学学报, 2014, 36(3): 156-163.

LI Cheng, WANG Wei, SHI Longfei, et al.Automatic recognition method of radar antenna scan type [J]. Journal of National University of Defense Technology, 2014, 36(3): 156-163. (in Chinese)

[5]赵立志, 魏永峰. 欺骗性雷达干扰实现方法分析[J]. 舰船电子对抗, 2013, 36(2): 11-13.

ZHAO Lizhi, WEI Yongfeng. Analysis of implementation method of deception jamming to radars [J]. Shipboard Electronic Countermeasure, 2013, 36(2): 11-13. (in Chinese)

[6]周庆昊, 严振华, 冀建民, 等. 有源航迹假目标欺骗干扰与不明空情研究[J]. 舰船电子对抗, 2013, 36(3): 27-31.

ZHOU Qinghao, YAN Zhenhua, JI Jianmin, et al. Research into active track false-target deception jamming and unidentified air intelligence [J]. Shipboard Electronic Countermeasure, 2013, 36(3): 27-31. (in Chinese)

[7]Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188.

[8]Crisan D, Doucet A. A survey of convergence results on particle filtering methods for practitioners [J]. IEEE Transactions on Signal Processing, 2002, 50(3): 736-746.

[9]Gustafsson F, Gunnarsson F, Bergman N, et al. Particle filters for positioning, navigation, and tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2): 425-437.

[10]杨争斌, 谢恺, 郭福成, 等. 基于角度约束采样的单站无源定位混合粒子滤波算法[J]. 电子与信息学报, 2008, 30(3): 576-580.

YANG Zhengbin, XIE Kai, GUO Fucheng, et al. Hybrid particle filtering algorithm for passive location by a single observer based on bearing constrained sampling [J]. Journal of Electronics & Information Technology, 2008, 30(3): 576-580. (in Chinese)

[11]王丽, 刘正军, 胡捍英. 基于粒子滤波的蜂窝网移动台单站跟踪[J]. 电子与信息学报, 2007, 29(7): 1556-1559.

WANG Li, LIU Zhengjun, HU Hanying. Particle filter for single base station mobile tracking in cellular networks [J]. Journal of Electronics & Information Technology, 2007, 29(7): 1556-1559. (in Chinese)

[12]郁春来, 占荣辉, 万建伟. 基于极坐标的稳定UKF单站无源目标跟踪算法研究[J]. 国防科技大学学报, 2008, 30(5): 73-79.

YU Chunlai, ZHAN Ronghui, WAN Jianwei. Research on robust UKF algorithm for single observer passive target tracking based on polar coordinates [J]. Journal of National University of Defense Technology, 2008, 30(5): 73-79. (in Chinese)

Estimate of radar beam′s azimuth using particle filter

LUShanshan1,2,WANGWei1,WANGGuoyu1

(1. College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China;2. State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System,National University of Defense Technology, Changsha 410073, China)

Abstract：Traditional estimate method has limited capacity when the scan rate of radar antenna varies with time. Thus a state space model for estimating beam azimuth was established, and the particle filter was introduced to estimate the state variables. Particle filter is a powerful method for state estimation in non-linear and non-Gauss case， the radar beam′s azimuth estimating algorithm based on particle filter has better performance, and it can adapt to the case where the scan rate of radar antenna varies with time. The simulation results show that the applicability and the efficiency of the proposed algorithm are desired.

Key words：radar reconnaissance; scan analysis; radar beam′s azimuth; particle filter

中图分类号：TN95

文献标志码：A

文章编号：1001-2486(2016)01-074-04

作者简介：陆珊珊(1986—)，男，安徽淮南人，博士研究生，E-mail：sslu2004@sina.com；王伟(通信作者)，男，教授，博士，硕士生导师，E-mail：13807319968@139.com

基金项目：国家自然科学基金资助项目(61201336)

*收稿日期：2015-06-04

doi:10.11887/j.cn.201601013

http://journal.nudt.edu.cn