基于对应分析法的《统计学》教学满意度实证研究

蔡宏宇

（湖南商学院数学与统计学院，湖南长沙410205）



基于对应分析法的《统计学》教学满意度实证研究

蔡宏宇

（湖南商学院数学与统计学院，湖南长沙410205）

摘要：《统计学》教学满意度评价有助于监测和监控《统计学》教学质量，有利于促进《统计学》教学方法改革，以提高学生学习和掌握《统计学》理论和方法的兴趣。本文采用抽样调查方法从湖南五所大学采集了876个有效样本，选择对应分析技术，从受访者总体、专业、院校、年级和性别等不同方面，对评价模型进行实证分析。研究结果表明：受访者总体满意度处于欠理想水平，统计专业受访者对《统计学》教学的满意度明显高于非统计专业，一类本科院校受访者对《统计学》教学满意度略高于二类本科院校；随着年级递升受访者对《统计学》教学满意度的认识更趋理性。

关键词：统计学教学；满意度；评价指标体系；对应分析法；加权平均法

《统计学》是一门搜集、整理、分析数据并进行推断的方法论学科，其理论较抽象、公式较繁琐，对学生专业技术性和实践性要求较强。要使得学生在一个学期内熟练掌握、融会贯通该学科所含知识点，教学方法至关重要。因此，在《统计学》教学过程中，学生满意度测评必不可少。基于此，本文立足学生视角，构建《统计学》教学满意度评价指标体系，采用问卷调查方式收集样本数据，选择对应分析方法，对《统计学》教学满意度进行测度分析，以期通过探寻当前《统计学》教学存在的不足，找寻可能改进的切入点，为《统计学》教学质量的提升提供有益参考。

一、《统计学》教学满意度评价指标体系构建

满意度也称满意指数，它是期望值与实际值之间的匹配程度。换言之，就是通过对一种产品或服务可感知的效果与其期望值相比较后得出的指数。那么，《统计学》教学满意度就可以理解为学生对《统计学》教学可感知的效果与其期望值相比较后得出的指数。它是测量《统计学》教学质量和学生掌握《统计学》课程内容的主要量化指标。它不仅与学生数学基础内因有关，而且受教师教学方法等外因的影响。国内外有关教学满意度研究成果不少，但关于《统计学》教学满意度研究非常少，主要集中于医学、经管类等专业统计教学满意度研究[1][2]，资料收集基本上都是采用问卷调查方式；研究主要集中于课堂教学，实践教学较少；评价方法较多，比较有代表性的方法：有关联分析、描述性统计分析方法和相关回归分析法[3][4]、因子分析法[5]等。

结合《统计学》教学实际，按照指标设计系统性和可操作性原则，在调查分析的基础上，根据《统计学》教学主要影响因素，全面反映统计专业的重视程度、《统计学》难易度、《统计学》学习条件、《统计学》教材选用、统计专业师资配备、《统计学》课程内容设置以及《统计学》理论教学与实践操作相结合等方面，构建涉及课程地位、教学条件、教学环境与内容、师资力量四个一级指标，包括12个二级指标的《统计学》教学满意度评价指标体系[6]。（详见表1）

表1　学生对《统计学》教学满意度评价指标体系

二、《统计学》教学满意度评价方法选择

（一）资料获取

鉴于《统计学》教学满意度评价没有现成数据资料，为充分了解学生对《统计学》教学的满意度情况，本研究以湖南5所大学（包括重点大学和二本高校）本科和研究生为调查对象开展问卷调查。本次调查根据构建的评价指标设计问卷，以满分10分制，分别统计专业和非统计专业、男女性别、包括本科二、三、四、研究生四个层次，要求学生对《统计学》教学12个二级指标，根据实际情况打分。选择时间节点为2014年9月学习过《统计学》课程的1000名学生进行抽样调查，回收有效问卷876份，获得《统计学》教学满意度测评相关资料，为满意度实证分析奠定研究基础。

（二）分析方法选择

有关满意度评价方法比较常用的包括加权平均法、模糊综合评判法、层次分析法、关联分析法等。为了使统计学教学评价能够科学、直接反映出原始数据所包含的内在信息，通过对前人相关研究方法的研判，本文选取对应分析法分析学生对统计学教学的满意度。

对应分析方法[7][8]又称相应分析，是在R型和Q型因子分析基础上发展起来的一种多元统计方法，也是利用降维的思想达到简化数据结构的目的，应用于由属性变量构成的列联表数据的研究，利用对应分析可以在一张二维图上同时画出属性变量不同取值的情况，列联表的每一行及每一列均以二维图上的一个点来表示，以直观、简洁的形式描述属性变量各种状态之间的相互关系以及不同属性变量之间的相互关系。

对应分析方法基本原理，是将R型因子分析与Q型因子分析结合起来进行统计分析，它是从R型因子分析出发，直接获得Q型因子分析结果。它克服了由样品容量大，作Q型分析所带来的计算上的困难。而且根据R型和Q型分析的内在联系，可将指标(变量)和样品同时反映到相同坐标轴(因子轴)的一张图形上，便于对问题进行比较分析。如在图形上邻近的一些样品点则表示它们的关系密切归为一类，邻近的一些变量点则表示它们的关系密切归为一类，而且介于同一类型的样品点，可用邻近的变量点来表征。因此，对应分析概括起来可提供指标之间、样品之间以及指标与样品之间三方面关系的信息。其基本步骤如下：

（1）设有n个样品，每个样品观察p个指标，原始数据矩阵为：

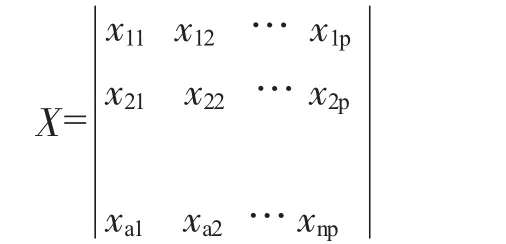
（2）对数据矩阵先分别按行和列求和，再求总和。

（4）进行R型因子分析，计算协方差矩阵的特征值，按其累计百分比取其前m个特征值，并计算相应的单位特征向量，从而得到R型因子载荷矩阵

5.进行Q型因子分析，对前m个特征根计算相应于矩阵的单位特征向量，得到R型因子载荷矩阵

6.在二维因子轴上作图。

三、《统计学》教学满意度评价结果及分析

根据调查结果，利用对应分析法，分析和测评876名学生对《统计学》教学满意度情况，结果发现：受访者总体满意度处于欠理想水平，统计专业受访者对统计教学的满意度明显高于非统计专业，一类本科院校受访者统计教学满意度略高于二类本科院校；随着年级递升受访者对统计教学满意度的认识更趋理性；不同性别受访者对《统计学》教学满意度差别不大。

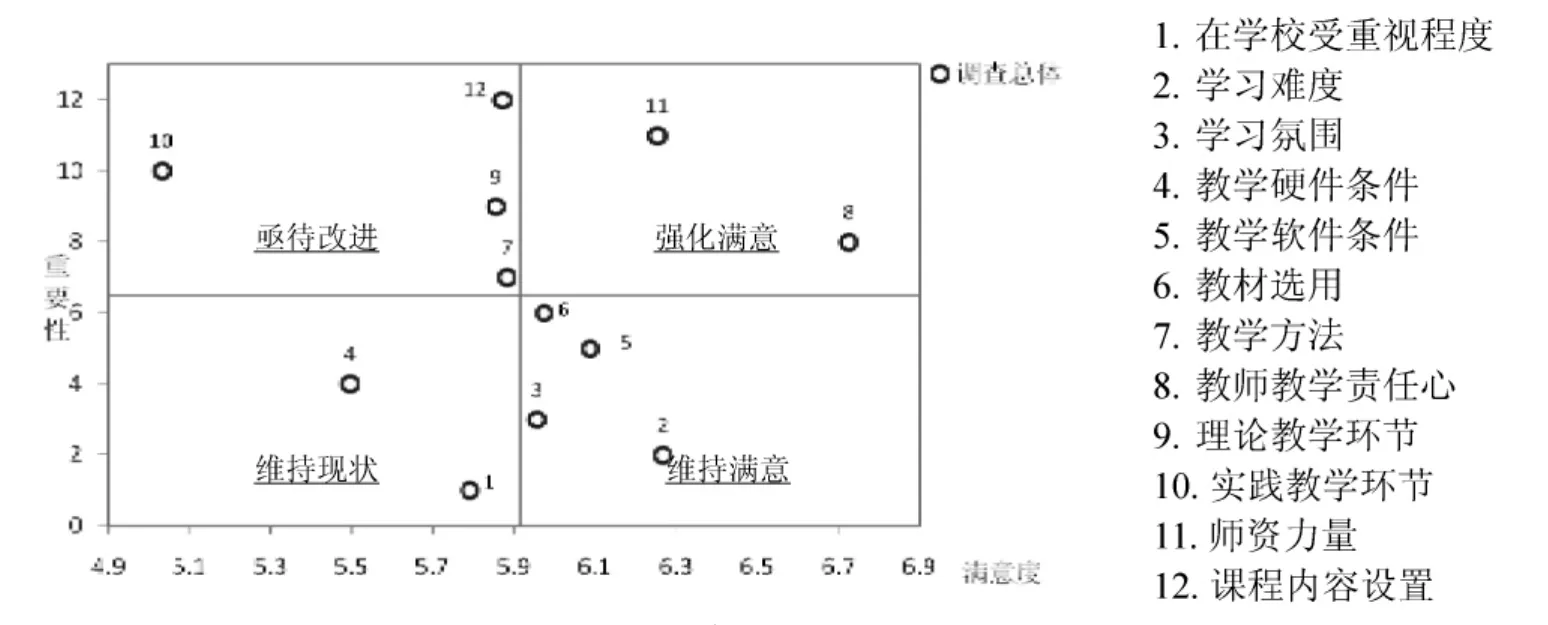
图1　受访者总体对统计学教学的满意度分析

（一）受访者总体满意度处于欠理想水平

根据《统计学》教学满意度评价四个方面：课程地位、教学条件、教学环境与内容、师资力量，12个二级指标的调查数据，采用加权平均法对受访者进行统计学教学满意度测评发现，总体满意度不够理想，受访者对统计学教学满意度综合得分仅5.93分，以10分为标准，满意度刚达及格水平。其中，对师资能力的综合评价最高，也只6.49分，其余三项综合评价得分分别为5.83分、5.79分和5.79分。

为更好地诊断《统计学》教学中存在的问题，在对各项具体指标满意度进行评价的基础上，结合各指标对受访者的重要性程度，利用表示对应分析矩阵，作进一步的定量分析。详见图1，总体显示，评价教学满意度12项指标中，各有一半的指标分别落在总体满意度得分（5.93）的左侧和右侧。结合指标重要性分析：仅有两项指标落在“强化满意”区，且均是对教学师资的评价指标，其中对教师责任心的评价为所有指标中得分最高（6.73）；其次，有四项指标落在“亟待改进”区，其中对《统计学》实践教学环节最为不满意，为所有指标最低（5.03），另有课程内容设置、统计教学方法及理论教学也落在这一区间；再次，在对重要性较低的指标评价中，受访者的满意度分布要优于重要性较高的指标，只有统计教学硬件条件和学院受重视程度两项指标，低于总体满意度。

具体分别对受访者专业、院校、年级及性别等属性特征，区分不同群体对统计学教学各指标的满意度差异，利用对应矩阵做进一步分析，有如下结论。

（二）统计专业受访者对统计教学的满意度明显高于非统计专业

见图2，统计专业受访者对统计学教学的综合满意度得分为6.44，高出非统计专业受访者5.51分近1分。通过对两群体12项教学满意度评价指标得分，经转换后进行Wilcoxon符号秩检验（p=0.000），可知两个群体对统计学教学评价满意度存在显著性差异。结合“分专业受访者在统计教学指标上的满意度”对应矩阵图，发现统计专业受访者对统计学教学满意度明显高于非统计专业。在12项评价指标中，统计专业受访者有11项指标得分落在综合得分线（5.93）的右侧，其中，教学软件条件、教师责任心及学习难度3项指标得分超过7分；而非统计专业受访者则有10项指标得分落在综合得分的左侧，且有统计实践教学环节、统计课程内容设置、统计教学方法及理论教学环节四项指标落在对应矩阵“亟待改进”区。比较两群体在各指标上的得分差发现，有教学软件条件、学习难度、学习氛围及教学硬件条件四项指标，非统计专业受访者满意度得分低于统计专业1分以上。

图2　分专业受访者统计学教学满意度对应矩阵图

（三）一类本科院校受访者《统计学》教学满意度略高于二类本科院校

一、二类本科院校受访者对统计教学的综合满意度得分分别为6.11分和5.74分，在各评价模块上，一类本科院校受访者的教学环节、专业投入及专业地位指标，高于二类本科院校。“分院校受访者统计教学指标满意度决策矩阵图”显示，在各评价指标上，一类本科院校受访者有10项指标落在综合得分线右侧，二类本科院校受访者则只有四项指标。同时，二类本科院校受访者的专业理论教学环节、专业实践教学环节及专业课程内容设置指标，均落在“亟待改进”区，详见图3。

图3　分院校受访者统计学教学满意度对应矩阵图

（四）随着年级递升受访者对统计教学满意度的认识更趋理性

本科阶段不同年级对统计教学满意度存在较大差异，详见图4。据调查，本科低年级、高年级及研究生受访者对统计教学的综合满意度得分分别为6.01分、5.68分和5.74分。“分年级受访者对统计学教学指标的满意度”对应矩阵图显示，随着受访者年级的递升，对统计教学各指标的满意度得分有着明显的影响。各指标的得分集中趋势随年级的递升不断离散，这在某种程度上说明了随着年级的递升，受访者对统计专业的认识更加理性，更加突出个性的见解和认知。

另外，调查发现，不同性别受访者对《统计学》教学满意度差别不大。男性受访者对《统计学》教学的综合满意度得分为5.92，与女性受访者5.94分相近。在各项评价指标上，男性受访者教师教学责任心、师资力量及教学软件条件等5项指标得分，均在综合得分线的右侧，女性受访者则有6项指标落在综合得分线右侧，详见图5。

（五）小结

将学生性别、专业、年级、学校类别等不同属性特征资料与其对统计学教学的满意度评价进行多重对应分析，从对应矩阵图（详见图6）可知，统计专业、男生、一类本科跟“满意”靠近；非统计专业、女生、二类本科跟“还可以”靠近；不同年级对《统计学》教学满意度相对分散，分布在不同的矩阵区域；专业和性别均分布在对称轴左右两侧；学校类别分布在对称轴上下两侧。

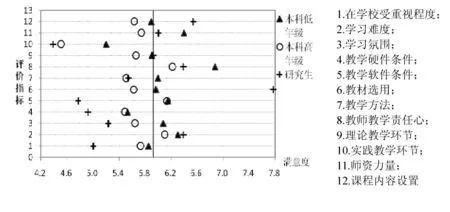
图4　分年级受访者统计学教学满意度对应矩阵图

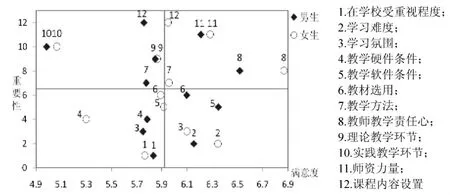
图5　分性别受访者统计学教学满意度对应矩阵图

可见，满意度的高低与受访者的专业、性别之间存在较高相关性，与学校类别存在一定相关性，而与年级高低则基本不相关。进一步分析比较发现满意度与受访者的专业高度相关，表现为其他专业学生对统计学教学满意度明显低于统计专业。从以下四个方面分析不同属性特征与《统计学》教学满意度多重对应矩阵图，其结果与各属性特征单个对应矩阵分析结果基本一致。

1.观察邻近区域。分析图6临近区域发现，统计专业、男生、一类本科跟“满意”靠近，非统计专业、女生、二类本科跟“还可以”靠近，满意度的高低与受访者的专业、性别之间存在较高相关性。

2.向量分析。据图6进行向量分析显示，从中心向任意点连线（向量），然后让所有的点往这条向量及延长线上作垂线，垂点越靠近向量正向的表示越趋向满意度评价。如统计专业、男生跟“满意”向量垂直正向距离最靠近。

3.向量的夹角——余弦定理视角分析。从余弦定理的角度看相似性，中心向任意两个点（相同类别）做向量的时候，夹角是锐角的话表示两个方法具有相似性，锐角越小越相似，钝角或平角表示非常大的差异。非统计专业、女性、二类本科均与满意构成钝角，说明非统计专业、女性、二类本科的满意度不高。

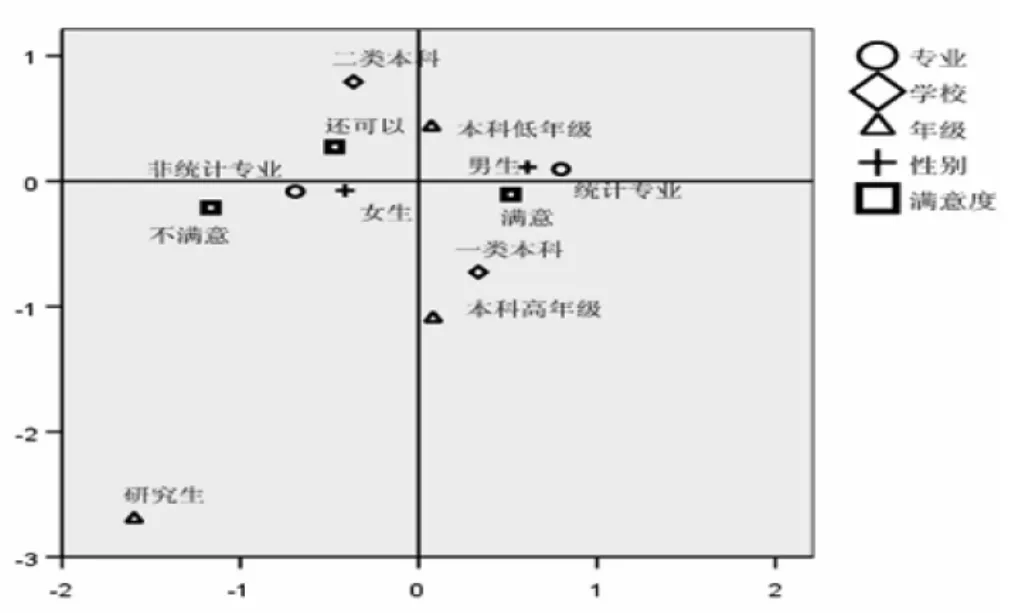
图6　受访者不同属性特征与统计学教学满意度多重对应分析

4.距离中点位置分析。从距离中点的位置分析发现，越靠近中心，越没有特征，越远离中心，说明特征越明显。研究生距离中心最远，表示研究生在专业、性别、学校类别、年级方面无明显相关。

分析调查结果，提高《统计学》教学满意度应从以下几方面考虑：根据不同专业设置《统计学》课程内容，施以不同教学方法，如案例可根据专业要求选择、联系学生本专业要求实际积极引导，提高学习兴趣；统计学课程可选择在高年级开设；在完成统计学理论教学的同时，加大实践教学力度，如增加统计绘图绘表、实证分析课时等。

参考文献：

[1]陈卫中，魏敏，杨书，杨晓虹.非预防医学专业本科阶段《医学统计学》教学满意度评价及建议[J].现代预防医学,2013(23).

[2]周银香.经管类专业《统计学》课程教学满意度的统计分析——基于多分有序Probit模型的实证研究[J].教育教学论坛,2014(23).

[3]赵伶俐,潘莉.高校学生对教学、任课教师和课程满意度的调查[J].重庆大学学报(社会科学版），2001(3).

[4]齐文娥，叶浪湖.教学服务公平性对教学质量、教学满意度的影响研究——基于广州市五所高校的实证分析[J].河北经贸大学学报（综合版）,2011(4).

[5]张蓓，林家宝.大学教学满意度影响因素实证分析——基于学生期望与学生感知质量的视角[J].复旦教育论坛, 2014(4).

[6]亢婷.对应分析法在课堂教学质量中的应用[J]．数学的实践与认识，2015(1).

[7]蔡伟.我国科技竞争力地区差异响应分析[J]．统计与决策，2015（8）.

[8]侯治平，白丁.对应分析法对电子商务网站评价的研究[J].生产力研究，2011（8）.

[9]王敬童.分层教学视角下《微积分》课堂教学满意度的实证研究——以湖南商学院为例[J].湖南商学院学报，2015（4）.

（责任编辑：周小红）

An Empirical Study on Satisfaction Degree of Students in Statistics Teaching Based on Correspondence Analysis

CAI Hong-yu
(School of Mathematics and Statistics, Hunan Universityof Commerce, Changsha, Hunan 410205)

Abstract：The satisfaction evaluation of statistics teaching helps to monitor and control the teaching quality of statistics, promote the innovation of teaching methods of statistics, and improve the students' interest in learning and mastering statistical theories and methods. We collect 1000 valid samples through a sample survey of five universities in Hunan province, and adopt corresponding analysis method for an empirical analysis on the evaluation model from the respondents as a whole, and other aspects such as major, universities, grade and gender. The research results show that the overall respondents’satisfaction is on a less ideal level, the satisfaction degree of respondents majored in statistics is significantly higher than that of the non-statistics major; the satisfaction degree of students in first-class undergraduate universities is slightly higher than that of the second-class undergraduate universities; Along with the ascending grade, the satisfaction degree of respondents gets higher.

Key words：statistics teaching; satisfaction degree; evaluation index system; correspondence analysis; weighted average method

作者简介：蔡宏宇（1964—)，女，湖南益阳人，湖南商学院数学与统计学院副教授。

项目基金：湖南省教育厅教研教改课题“基于‘案例导入式’的《统计学》课程教学模式创新研究”。

收稿日期：2015-11-08

中图分类号：G642.3

文献标识码：A

文章编号：1008- 2107(2016)01- 0109- 06