浅谈如何在教学中培养学生的直觉思维能力
2016-04-07广东广州市越秀区署前路小学510080游家水
广东广州市越秀区署前路小学(510080)游家水
浅谈如何在教学中培养学生的直觉思维能力
广东广州市越秀区署前路小学(510080)游家水
[摘要]直觉思维是思维的一种基本形式,是一种非形式化的,以高度省略、简化、浓缩的方式洞察问题实质的思维。教师在教学中充分利用习题来培养学生的直觉思维,提高学生解题的能力。
[关键词]小学数学直觉思维能力培养
直觉思维是思维的一种基本形式,是人们以一定的知识、经验、技能为基础,通过观察、联想、类比、猜想等方式对所研究的问题迅速做出判断。它具有灵活性、自由性、创造性、自发性和偶然性的特点。直觉思维的培养对全面提高学生的思维能力,特别是创造思维能力意义重大。因此,我结合教学实际,谈谈如何培养学生的直觉思维能力。
一、深入观察,洞悉实质
课本中的例题或习题,往往会出现一题多解的情况。这时,在学生学习一般解题方法后,教师可引导学生仔细分析题目,让学生找出更为简便的解题方法。
例如,教学中的一道练习题:玩具厂原计划每天生产玩具320个,9天可完成生产任务。实际只用了8天就完成了,实际每天比原计划每天多生产玩具多少个?
此题的常规解法为:先求出总任务为320×9=2880(个),再求出实际每天生产的个数为2880÷8=360(个),最后求出实际每天比原计划每天多生产的个数为360-320=40(个)。在学生学习了常规的解法之后,我引导学生:“换个角度思考,你能找出更简便的方法吗?”学生很快接受挑战,重新分析题目,认真思考,并讨论交流后,得出:原计划9天完成的任务,现在只需要8天可以完成,即提前1天完成任务。这一天的生产任务320个应该分配在实际的8天内,所以平均每天要多完成玩具的个数为320÷8=40(个)。
学生挑战成功后,顿时信心十足,跃跃欲试运用多种解法解题,于是,我趁机给出另一练习题:小明原计划20天生产320个零件,实际每天比原计划多生产25%,实际几天可以完成生产任务?
这时,我先带领学生按照常规解法解题:320÷[320÷ 20×(1+25%)]=16(天)。学生在学习常规解题方法后,对题目重新剖析,从另一个角度思考问题,经推理得:工作总量是320个不变,工作效率与工作时间成反比例,假设原来的工作效率是“1”,那么现在的工作效率是原来的(1+25%)=,现在的工作时间是原来工作时间的1÷=,因为原来需要20天完成,所以现在需要20×=16(天)。通过一题多解的训练,学生的解题思路更加开阔,思维更加活跃。之后,学生在解题时,养成了多种角度去思考问题的习惯,增强了学生的解题能力。
在教学中,针对一题多解的习题,教师需要引导学生分析已知条件、问题的结构、图形的变化规律和题目所给出的数据关系等信息,让学生洞察数量关系和结构关系,进行跳跃性思维,缩减某些推理环节,增强直觉意识,达到提高直觉思维能力的目的。
二、善于联想,促进迁移
联想是直觉思维的一种常见思考方法,是以一定的知识、生活经验及技能为基础,让学生对某些数学问题展开联想,并将思维迁移,找到更快捷、简便的解题方法。
例如,在教学中我给出的一道题:求下图(图1)中两圆阴影部分面积的差。
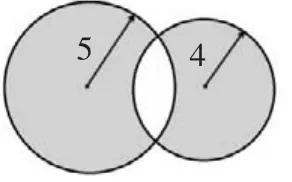
图1

图2
学生分析题目后,一时无计可施。于是,我引导学生展开联想,间接求出答案。学生得到启发后,很快就依据“被减数、减数都同时加上或减去同一个数,差不变”的道理,联想到:(大圆阴影部分的面积+公共部分面积)-(小圆阴影部分的面积+公共部分面积)=大圆面积-小圆面积,两圆阴影部分面积的差就是两圆面积的差。这时,我让学生重新画图,把处于静止状态的两个圆进行“平移”(图2),使圆心重合,得到一个圆环,这个环形面积就是原来图中阴影部分面积的差。
学生学会联想迁移的解题方法后,运用于其他题目中同样得心应手,能很快找到问题的答案。如:小明的书比小东的书多12本,小明借出自己所有的书的,小东借出自己所有的书的后,两人余下的书的本数相同,两人原来各有书多少本?
学生通过挖掘题目中的隐含条件,联想到:小明书本数与小东书本数的比是多少?题中小明书本数的(1-)等于小东书本数的(1-),得到小明书本数与小东书本数的比是,因此,学生得出答案,小明的书本数为:(本),小东的书本数为:48-12=36(本)。
在课堂教学中,教师善于引导学生展开联想,让学生学会将思维迁移,使学生能更快地找到解题的关键。这不仅能提高学生的直觉思维能力,还能激发学生学习数学的兴趣。
三、类比推理,出现顿悟
类比是一种常用的推理方法,而顿悟是直觉思维的一种表现形式。教师在教学中合理运用类比的推理方法,让学生由此及彼,找出解决问题的关键,出现顿悟,达到解题的目的。
例如,在教学中有一道练习题:计算下图中阴影部分的面积。
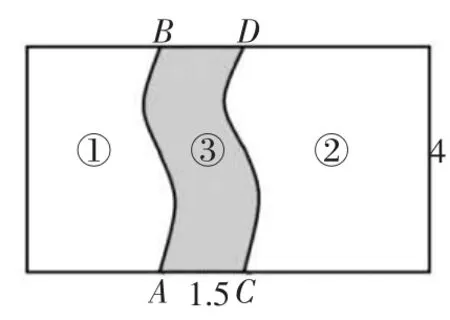
图3

图4
学生观察图形后发现阴隐部分是一个不规则的图形,不能用一般的图形面积公式求解。于是,我提示学生:“可以通过平移,将阴影部分的面积拼成一个规则的图形吗?”学生听后,恍然大悟,观察发现曲线CD与曲线AB弯曲程度相同,可以把图3中的②向左平移,使曲线CD与曲线AB重合得到图4,阴影部分的面积就变成了一个长方形③,很快就求出了答案。我为学生如此快速的学会类比和迁移的方法而高兴。
为了让学生熟练地运用类比的方法解题,我又给出一道练习题:(如图5所示)已经AB=10分米,求阴影部分的面积。
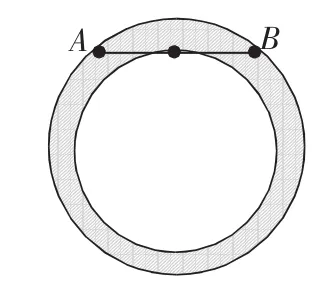
图5

图6
学生分析题目后,发现题目已知条件并没有给出两个圆的半径,因此,不能使用常规的方法(大圆面积-小圆面积=圆环面积)来解答。这时,我鼓励学生运用类比的思想来思考,并提示学生先画出辅助线。学生受到启发后,将圆心O分别和A、H点相连,得到图6,由勾股定理得出:OA2-OH2=AH2=52,所以,圆环的面积为:3.14×52= 78.5(平方分米)。之后,学生以运动的思想来思考,还能得出另一种解题方法:将AB中的H向圆心靠拢使内圆缩小为一个点,这时,AB成为外圆的直径,也能求出圆环的面积。
由此,教师在教学中鼓励学生使用类比的思想去解题,让学生在解题过程中产生顿悟,使学生的直觉思维得到发展。
四、数形结合,诱发直觉思维
教师在教学中,注重引导学生利用数形结合的方法解题,对培养学生思维的敏捷性大有益处,使学生的直觉思维得到锻炼。
例如,在教学中有一道例题:A、B、C、D、E五个足球队参加单循环比赛,已知A、B、C、D四队分别赛了4场、3场、2场、1场,问E队赛了几场?
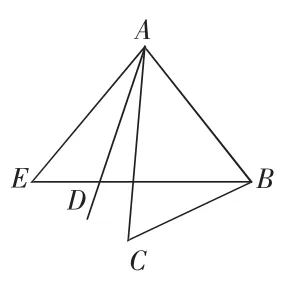
图7
学生看到题目后,发现题中的已知条件非常多,一不小心就有可能出错。于是,我引导学生将题中的已知条件用图形表示出来。很快,学生就画出了如上图所示的图形(图7),通过图形,可以直观看出E队赛了2场。
通过以上的学习,学生体会到数形结合的方法能使题目简洁明了,更有利于得出答案。在之后的学习中,学生利用数形结合的方法,还能找到繁琐的计算题的答案。如“计算的和”。学生审题后,发现常用的通分方法非常的麻烦,而且不切实际。于是学生想到利用数形结合的方法解题,他们先画出一个正方形,设大正方形的面积为1,如图8所示。
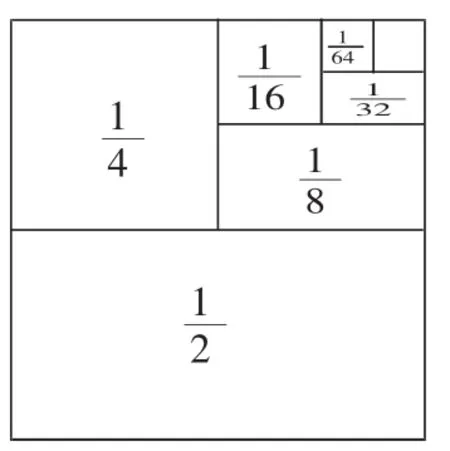
图8
教学过程中,教师利用数形结合的方法,将抽象转化为直观。通过直观图形学生更易理解,能更快地吸收,从而提高学生的直觉思维。
总之,在数学教学中,教师要引导学生认真观察、留意捕捉、充分联想来提高学生利用数形结合和类比的方法解题的能力,培养学生的创新意识,进而提高学生的直觉思维能力。
(责编莫秋鸿)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)05-073
