问题驱动:从此岸走向彼岸——以“和与积的奇偶性”为例
2016-04-07江苏海安县实验小学226600
江苏海安县实验小学(226600)顾 荣
问题驱动:从此岸走向彼岸——以“和与积的奇偶性”为例
江苏海安县实验小学(226600)顾荣
[摘要]教师将学习的目标问题化,让新知学习成为一个项目研究,促使学生发现问题、提出问题、分析问题、解决问题。以问题激发学习动机,彰显学生主体地位;以问题聚焦学习内容,凸显学习目标;着力问题解决,培养探究能力;围绕问题展示,促进良性互动;强化反思梳理,发展元认知能力。
[关键词]问题问题解决探究能力数学素养
学生的认知发展过程是一个不断将未知转化成已知的过程。未知领域的知识有可能是“要求回答或解释的题目”,也可能是“需要研究讨论并加以解决的矛盾、疑难”。在教学过程中,教师可以将这些未知知识教授给学生,也可以将其转化为一个又一个“问题”让学生去研究、探索,让学生在解决问题的过程中掌握新知。在小学数学学习过程中,许多未知的数学知识都可以看做是学生需要解决而未解决的问题,包括摆在学生面前需要掌握的新知识,需要不断完善的认知结构,解决数学问题必备的方法技能,以及学生需要自我关照的元认知能力,等等。这些问题会让学生产生一种对学习内容的不解的认知状态,这样的状态使教学形成了强大的张力。因此教师要突出“问题”的作用和地位,教学全程都要体现知识问题化、目标问题化的理念,追求“问题”为主线的教学,用问题来驱动教学。将学习内容创设成系列的、环环相扣的问题,用问题激发学生学习数学的原动力,能把学生的思维引向深处,从而最大限度地激发他们体验和理解数学学习内容的本质,形成良好的数学素养。下面以“和与积的奇偶性”教学为例谈谈个人的实践和思考。
一、破题,用问题指引方向
师:明天我们将研究“和与积的奇偶性”,看到这个课题,你会提出哪些问题?你会想到哪些相关知识?
生1:与加法有关,与乘法有关。
生2:与奇数、偶数有关。
师:能具体说说你的猜想吗?
生3:就是研究加法中的和是奇数或偶数的情况,乘法中的积是奇数或偶数的情况。
师:加法也好,乘法也好,都有简单与复杂之分,你将采取怎样的研究策略呢?
生4:先研究两个数相加的和的奇偶性,接着研究三个数连加的和的奇偶性,再研究四个数、五个数连加的情况……乘法也是这样,先简单再复杂。
师:还有什么问题吗?
生5:和与积的奇偶性有怎样的规律,和的奇偶性的规律与积的奇偶性的规律有什么联系和区别?
师:其实我们要研究的一个核心问题就是——和与积的奇偶性有怎样的规律?请大家将这个问题作为研究的课题,回家完成课前导学单。
【思考:教师将学习的目标问题化,让新的学习成为一个项目研究,促使学生发现问题、提出问题,寻求到研究的大致方向,从而为学生的研究探索聚焦。】
二、导学,用问题规划方案
1.试一试,我能行
(1)两个数相加,什么情况下和是奇数?什么情况下和是偶数?你能举出一些合适的例子来研究其中的规律吗?
通过研究,我的发现是()
(2)几个数连加,你又是怎样研究的?你有什么困惑吗?
我重点研究的是()个数连加
我的发现是()
我想提醒大家的是()
我的困惑有()
2.说一说,我收获
把你的发现说给爸爸妈妈听,再听听他们的意见,对自己的理解会有帮助哦!
3.做一做,我超越
(1)连续10个自然数的和是奇数还是偶数?连续40个奇数的和呢?
我是这样想的()
(2)学校车棚里有一些自行车和三轮车,轮子的总数和车辆数都是奇数,那么自行车的辆数是奇数还是偶数?三轮车的辆数呢?(建议将自己的思考过程通过适当的方式展示出来)
【思考:课前问题导学,将学习内容进行问题化、板块化、方案化的处理,聚焦于教学的核心内容,这样有利于学生分析问题和解决问题能力的发展。本课题的研究内容主要是和的奇偶性和积的奇偶性。课前的导学单上,主要出现的是和的奇偶性的研究内容,这是教者精细设计的,因为和的奇偶性的研究较为复杂,需要从简到繁不断推进,而积的奇偶性可以在和的奇偶性的基础上实现迁移。因此,导学单上将学习内容以问题的形式设计了三个层次:一是用举例的方法研究两个数相加的和的奇偶性;二是选择性地研究连加的和的奇偶性;三是揭示和的奇偶性的规律。这样的问题具有方案性,使学生的研究从简到繁,既有利于问题的解决,学生的认识也会得到不断提升。同时,所设计的问题注重了方法的指导,如用给出具体例子的方法来研究规律,选择性地研究连加的和的奇偶性,突出研究的重点、发现和困惑,把自己的研究发现向爸爸妈妈介绍并寻求他们的帮助,等等。】
三、交流,展示问题解决的过程
1.研究两个数相加的和的奇偶性
师:小组内交流课前研究的情况,说说你是从哪入手的?
生1:先研究两个数相加的情况,我是用举例的方法来研究的。
奇数+偶数:1+2=33+6=95+18=23
奇数+奇数:1+3=43+7=1113+57=70
偶数+偶数:2+4=66+8=1410+20=30
师:两个数相加的和的奇偶性有怎样的规律呢?
结论:(1)奇数+偶数=奇数;(2)奇数+奇数=偶数;(3)偶数+偶数=偶数。
师:光有几个例子好像不够严谨,再举例子好像又举不完,你能解释吗?
生1:其实很简单!偶数除以2没有余数,奇数除以2余数是1。(1)中相除后有余数1,所以和是奇数;(2)中两次相除都有余数1,相加就是2,也就是说合起来再除以2就没有余数了,所以和是偶数;(3)就不用解释了。
师:大家都听明白了吗?
【思考:课内的师生互动应高于课前学生的自主学习的收获,因此新的问题“你能解释吗?”不是低层次的重复,而是新的认识。课堂教学的价值,应体现在学生认识的提升上。在展示了学生研究的结论之后,教师提出新的问题“光有几个例子好像不够严谨,再举例子好像又举不完,你能解释吗?”让学生在解释中认识得到了提升——从感性走向理性,从归纳走向说理。】
2.研究几个数连加的和的奇偶性
师:研究连加的和的奇偶性,你重点研究的是几个数相加?采用的是什么方法?(分别请研究3个数、4个数、5个数连加的学生或小组向全班介绍研究结果。汇报的情况显示,学生研究几个数连加的和的奇偶性基本上还是采用的举例法。)
师(在肯定学生方法的基础上):能不能不举例子,利用两个数相加的和的奇偶性的规律,去揭示几个数连加的和的奇偶性的规律呢?
师:四个数连加有几种情况?
①奇数+奇数+奇数+奇数;②奇数+奇数+奇数+偶数;③奇数+奇数+偶数+偶数;④奇数+偶数+偶数+偶数;⑤偶数+偶数+偶数+偶数。
生1:⑤偶数+偶数+偶数+偶数=偶数;①奇数+奇数+奇数+奇数=(奇数+奇数)+(奇数+奇数)=偶数+偶数=偶数。
生2:②奇数+奇数+奇数+偶数=奇数+(奇数+奇数)+偶数=奇数+偶数+偶数=奇数+偶数=奇数。
生3:③奇数+奇数+偶数+偶数=偶数+偶数+偶数=偶数。
生4:④奇数+偶数+偶数+偶数=奇数+偶数=奇数。
【思考:学生课前是采用举例法研究连加的和的奇偶性的。交流后教师用新的问题“能不能不举例子,利用两个数相加的和的奇偶性的规律去揭示几个数连加的和的奇偶性的规律呢?”驱动学生向认识的更深处进发,促进学生充分利用掌握的规律去解释说明更为复杂的情况。】
3.揭示和的奇偶性
(1)师:连加时和的奇偶性可能跟什么有关?
生1:与前两个数的和有关。
生2:与加数中奇数的个数有关。
(2)独立完成下表
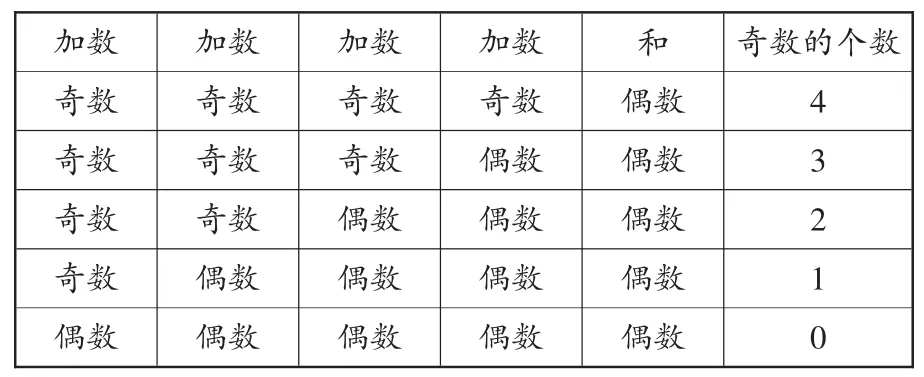
加数 加数 加数 加数 和 奇数的个数奇数 奇数 奇数 奇数 偶数 4奇数 奇数 奇数 偶数 偶数 3奇数 奇数 偶数 偶数 偶数 2奇数 偶数 偶数 偶数 偶数 1偶数 偶数 偶数 偶数 偶数 0
(3)验证多个数连加的情况后回答之前提出的问题。
(4)结论:几个数连加,加数中奇数的个数是奇数时,和是奇数;加数中奇数的个数是偶数时,和是偶数。
【思考:在学生分别用举例法和说理法逐步研究了两个数相加、几个数连加的和的奇偶性之后,教师用新的问题“连加时和的奇偶性可能跟什么有关?”将研究推到一个新的高度。通过填表归纳出和的奇偶性的规律,使学生经历从感性向理性升华的认识过程。】
四、迁移,将问题研究扩展
师:下面每道算式的结果是奇数还是偶数?你有什么发现?
3×5,4×6,3×7×2,3×7×2×6
师:下面的连乘算式的积是奇数还是偶数呢?
3×5×7×9×11×23×35
3×5×7×9×11×23×35×17×4×513
生1:只要因素中有偶数,积就一定是偶数。
师:如此看来,判断连乘的积的奇偶性,关键看什么?
结论:连乘时,因数中只要有偶数,积就一定是偶数;如果因数中没有偶数,积就是奇数。
【思考:在探索和的奇偶性规律的基础上,通过几道具体的乘法计算题,利用“判断连乘的积的奇偶性,关键看什么?”这个问题,使简约研究的过程直抵结论,体现了问题的力量!】
五、反思,让研究再次升华
师:和的奇偶性与积的奇偶性有什么异同?
生:和的奇偶性,看加数中奇数的个数,如果有奇数个奇数,那么和就是奇数;如果有偶数个奇数,那么和就是偶数。积的奇偶性,只要看因数中有没有偶数,只要因数中有偶数,那么积就一定是偶数;如果因数中没有偶数,积就是奇数。
师:你有新的理由吗?运用所学知识解释课前问题导学单上的最后一道题。(略)
【思考:课末的反思性问题,既与课首的问题形成呼应,又是对所学内容的应用,可以促进学生元认知能力的提高。】
好课的基因有若干个,但有一个基因是永远都存在的——问题设计。劳凯声教授认为:“问题是介于认识的此岸和彼岸之间的认知对象,如果它完全处于此岸,已被我们解决了,就不称其为问题;如果它完全处于彼岸,我们完全没有接触到、意识到,也就不能称其为问题。因此,问题应该是介乎认识的此岸和彼岸之间,被我们接触到、意识到并试图回答、解释,或者采取相应行动的这一类认知对象。”鉴于以上的认识,我们可以这样认为:首先,问题意味着矛盾和不平衡,即在认识的此岸存在着困惑;其次,问题意味着意义和完善性,即在认识的彼岸得到了解决;再次,问题意味着探究和建构性,即从认识的此岸走向彼岸;最后,问题意味着批判和反思性,即发展学生的解决问题思维。因此,教学中,教师应科学设计问题,以激发学生的学习动机,彰显学生的主体地位;以问题聚焦学习内容,凸显学习目标;着力问题解决,培养学生的探究能力;围绕问题展示,促进学生的良性互动;强化反思梳理,发展学生的元认知能力。通过问题驱动,让学生从认识的此岸走向胜利的彼岸。
(责编金铃)
[中图分类号]G623.5
[文献标识码]A
[文章编号]1007-9068(2016)05-007
