模型思想在解决问题教学中的运用

江苏盐城市中兴实验学校（224000）徐　娟



模型思想在解决问题教学中的运用

江苏盐城市中兴实验学校（224000）徐娟

［摘要］数学模型思想的运用是学生体会和理解数学与外部世界联系的基本途径。教师若能把模型思想渗透于解决问题教学中，则不仅可以优化学生的解题思路，而且可以显著提升教学效果。

［关键词］小学数学数学模型思想解决问题教学运用

数学模型是用数学语言概括或近似地描述现实世界事物的特征、数量关系以及空间形式的一种数学结构。解决问题作为学生的重要学习内容，教师要注重在其中渗透模型思想。经常进行利用模型思想解决问题的练习，对于提升学生解题能力、增强其应用意识具有显著促进作用。下面我就模型思想在解决问题教学中的具体运用谈谈自己的教学体会。

一、借助情境，从“生活原型→数学模型”，感知数学模型思想

在解决问题教学中，许多问题与学生的日常生活关系密切。教师可从学生已知的生活原型入手创设恰当的情境，使学生在生活情境的触发下把抽象的数学问题转化为数学模型，并应用数学模型思想来解决具体问题，从而提高学习效果。

如教学“平均分”时，我创设了这样一个学习情境：体育课上，老师拿来一些跳绳让学生（共54人）练习，请问这些跳绳应该如何分配？经过思考，学生认为这道题没有告知跳绳的具体数量，没办法分。此时，教师趁机追问：“怎样才能知道跳绳的总数？如果让你来分，你会怎样分？”在教师的追问下，学生说：“首先要数一数跳绳的总数，然后再根据学生人数进行平均分，这样才公平合理。”教师通过“创设问题情境→提出方法→平均分→公平合理”的学习过程，有效地促进了学生对“平均分”这一概念的认识。

由上述教学案例可以看出，生活情境的创设能唤醒学生的已有知识和经验，使其真正经历数学知识从生活原型到数学模型的形成过程，帮助学生初步感知数学模型思想的应用。

二、引导发现，从“分析比较→抽象综合”，建立数学模型思想

在解决问题教学中，除借助情境帮助学生感知数学模型外，教师还要善于引导学生进行分析和比较，提取有价值的信息，并综合运用到解题过程中。这样教学，有助于学生快速建立起相应的数学模型，发现解决问题的具体策略。

如在“圆的面积”的课后练习中有这样一道题：

下面三个正方形的边长都是3厘米，涂色部分的面积相等吗？为什么？

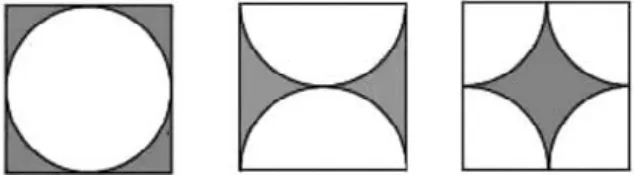
刚看完题目时，学生习惯性地想运用圆的面积公式来解答。但仔细读题后，学生发现这个方法不可行。于是我让他们观察、比较这些图形，思考它们的空白部分有什么特点、要求涂色部分的面积除了常规的直接求解方式外还有什么方法。在我的提示下，学生经过观察、分析和思考，建立起“涂色部分面积＝正方形面积—空白部分面积”这个关系模型。

在上述解决问题的教学案例中，教师没有直接把解题的方法告知学生，而是在引导学生仔细观察图形的基础上，鼓励学生自己去分析这些图形的异同点。这样教学，从分析比较到抽象综合，使学生亲历数学模型的建立过程，能强化学习效果。

三、探寻本质，从“表述过程→分享经验”，深化数学模型思想

在学生的数学学习中渗透模型思想的根本目的是让学生在探寻数学规律的过程中发现知识的本质特点，帮助学生学会运用模型思想来解决具体问题。因此，教师要在帮助学生在探寻知识本质、建构数学模型的基础上，更有效地把握解题策略，深化数学模型思想。

如“百分数的认识”的课后练习中有这样一道习题：

从题目可以看出，教材先从简单的“百分之几”这个数学模型入手，随后又启发学生从药品市场抽检合格率的变化情况谈谈自己的认识。教师若顺应教材的设计思路，引导学生表述自己的解题思路与想法、分享学习成果，可促进学生发现知识的本质与规律。当学生真正探寻到解决问题的本质与规律时，他们就不只学会了解决问题，更积累了基本的模型构建经验，深化了对数学模型思想的认识。

数学教师要善于引导学生在解决问题的过程中构建数学模型，鼓励学生将之进行内化并迁移运用，从而提高学生的思维能力，为学生的终身发展奠定基础。

（责编吴美玲）

［中图分类号］G623.5

［文献标识码］A

［文章编号］1007-9068（2016）05-048