基于经验模态分解的通信辐射源分形特征提取算法
2016-04-07桂云川杨俊安吕季杰
桂云川,杨俊安,吕季杰,王 伟
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
基于经验模态分解的通信辐射源分形特征提取算法
桂云川1,2,杨俊安1,2,吕季杰1,2,王伟1,2
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
摘要:针对当前通信辐射源个体识别方法精度不高,鲁棒性不强等问题,提出了基于经验模态分解(EMD)模型的通信辐射源特征提取算法。该算法通过提取包括本征模函数(IMF)时域和频域范围内的分形特征结合Hilbert边缘谱上的分形特征与谱对称系数组成特征向量,并使用支持向量机(SVM)得到分类结果。10部建伍电台的分类实验结果表明:该算法在不需要先验信息的前提下,可以得到较好的分类效果,并且具有一定的鲁棒性。
关键词:通信辐射源;特征提取;经验模态分解;分形特征
0引言
通信辐射源个体识别技术是通信对抗领域内的一个研究热点,通信辐射源的特征提取也是其中的一个难点问题。辐射源特征按照工作状态又可以分为暂态特征[1-2]和稳态特征[3-4],由于暂态特征在工程运用上的局限性[5],使得稳态特征成为了主要的研究方向,其中散特征的研究也成为了研究的热点。杂散特征是由于辐射源内部硬件的离散性所带来的,杂散成分一般隐藏在主要信号之下,因此直接从接收信号中提取杂散特征有一定的难度。此外,在电台的实际使用中,电台的工作频率总是处在交替的变化当中,电台的说话人以及所处位置也不是一成不变而是动态变化的,如何使得电台识别的方法可以排除电台工作条件等外部因素干扰,具有较强的鲁棒性也是电台识别方法研究过程中亟待解决的一个实际问题。
1998年,Norden E,Huang等人提出了经验模态分解(EMD)算法[6]。该方法是一种非常适合于非线性、非平稳信号的后验性自适应时频分析方法,在生物信号、机械及电路故障诊断方面都有诸多运用[7-9]。近期已有部分学者将EMD算法用于信号的特征提取,其中,文献[10]使用EMD分解后提取网格分形数作为生物信号的指纹特征并通过对比实验证明了该方法优于基于小波变换的分形特征提取算法。但由于通信辐射源内部情况复杂,仅仅提取单一特征无法充分反映辐射源内部的细微特性,导致最终的识别精度不高。文献[11]采用EMD算法将稳态信号的主要信号成分与杂散成分分离开来,然后提取杂散成分频域的能量作为信号的细微特征,避免了细微的杂散特征被主信号特征所淹没,但该方法使用快速傅里叶变换(FFT)的方法并不能精确有效的反映信号在频域范围内的信息,受噪声及环境因素影响较大,算法鲁棒性不强。针对上述问题,本文提出了基于EMD模型的分形特征提取算法,较前文算法不仅提升了识别率,而且对于不同工作环境下的电台识别具有一定的鲁棒性。
1基于EMD分解模型的基本理论
1.1EMD算法的基本原理
EMD算法能够自适应地将一个复杂信号分解成一组稳态和线性的本征模函数(IMF),对信号自身的尺度特征进行分解,并在分解的过程中保留了数据本身的特性,具有良好的局部适应性。其算法的本质是对信号进行平稳化处理,通过分解将具有不同时间尺度的信号分配到不同阶层的模态中。
图1给出的是某一电台信号经过EMD分解后前4阶的IMF波形图。

图1 EMD算法对于信号分解的结果Fig.1 The result of the EMD algorithm for signal decomposition
从图1可以看出IMF是直接从原始时序数据中分离开的,它反映了原始信号在某种特定意义频段范围内时域信息,通过对各阶IMF进行特征提取可以反映出信号在时域范围内的细微变化特性。
1.2瞬时频率的计算
此前在传统的频域分析中,主要采用的方法是傅里叶变换,基于傅里叶变换也衍生出了大量的时域与频域分析方法。但傅里叶变换属于局部变换,通过信号在一段时间上的积分求得,然而这对于求解瞬时频率没有意义。2009年Huang等人基于归一化方案提出了直接正交方法计算瞬时频率[12],该算法通过一种基于经验的归一化方案将IMF的调幅分量与调频分量区分开,然后利用经验调频分量求得与之相对应的正交函数,最后通过反正切函数得到相位函数进而得到相应的瞬时频率,其计算过程如下:
步骤1:通过归一化方案分离信号的调幅分量A(t)和调频分量F(t);
步骤3:将正交函数与调频分量作商并求反正切函数得到对应的相位函数:
(1)
步骤4:根据瞬时频率的定义可以得到:
(2)
瞬时频率表示的是信号在每一个时间点上瞬时频率的大小,通过对瞬时频率进行特征提取可以反映出信号内部的细微特征。
1.3Hilbert边缘谱
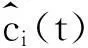
(3)
Hilbert谱是表示时间、频率与幅度关系的三维谱图,记做H(ω,t),对Hilbert谱的时间进行积分可以得到Hilbert边缘谱h(ω):
(4)
式(4)中,T为信号采样持续时间。h(ω)是一个时频函数,它表示了信号在每个频点上的幅值大小。通过对Hilbert边缘谱的特征提取可以反映出频域范围内的细微特征。
2基于EMD模型的特征提取算法
本文采用的算法如图2所示,先将原始信号进行EMD分解,对得到的本征模函数提取三类不同的特征:第一类提取IMF上的分形特征作为特征;第二类提取IMF对应瞬时频率包络上的分形特征;第三类提取Hilbert边缘谱上的对称系数与分形特征。将上述三类特征组合成特征向量,使用支持向量机(SVM)作为分类器进行分类识别。

图2 本文采用的算法流程图Fig.2 Algorithm flow chart in this paper
2.1分形特征提取
从时域波形中直接提取的特征受噪声变化的影响较大,在信噪比(SNR)未知的情况下,所提特征的分类效果十分不稳定,然而从信号EMD分解后的IMF波形中提取反映其几何分布特性的分形维数能够克服这个缺点。分形特征可以深入地刻画杂散调制对信号幅度、频率和相位的影响,提高了信号的分类效果。本文所提的分形特征包括盒维数、信息维数以及Lempel-Ziv复杂度。这三类特征在之前的研究中已经被证实是进行个体识别的有效特征。
盒维数是一种形态分形维,一个尺寸为ε的物体,其特征数N(ε)的变化关系为
N(ε)∝ε-D
(5)
式(5)中,D是分形维数。设F是Rn中任一有界非空子集,记N(A,δ)表示最大直径为δ且能覆盖F的集合的最小数,则F盒维数定义为:
(6)
其中盒维数反映了分形集的几何尺度情况,用来表示信号的不规则量度,却不能反映信号在平面空间的分布疏密,而信息维数能够体现分形集在分布上的信息,反映了信号在区域内分布的疏密情况。
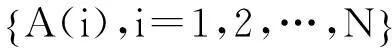
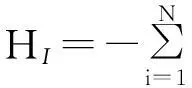
(7)
作为F的位形熵,若信息熵满足下面关系:HI~lgδDI,则F的信息维数定义为
(8)
从盒维数与信息维数的定义可以看到,盒维数是信息维数的特例。在等概率的情况下,盒维数等于信息维数,故由两者组成的特征向量包含了信号幅度、频率与相位的变化特征。
Lempel-Ziv复杂度通过复制和添加两种操作来描述信号序列的特性,并将所需的添加操作次数作为序列的复杂性度量。根据算法原理,如果序列的复杂度越小,则说明在复杂度运算过程中添加的操作次数少,序列发生新变化的速率越慢,周期性越强;反之,复杂度越大,发生新变化的速率越快,体现出的是序列变化的复杂性。从这个意义上来说,Lempel-Ziv复杂度可以刻画出信号波形的变化规律,可以作为一种有效的特征。
2.2Hilbert边缘谱对称系数提取
频谱的谱对称性是信号频谱的一个重要特征。由于电台内部本振频率不纯以及器件的非线性,使得内部噪声必然会有一部分以频率调制的方式附加在有用信号上,虽然这部分调制信号的能量相对较弱,但对于相同型号相同工作模式的电台来说,这些附加的调制必然会导致谱域产生细微差别,信号频域的谱对称性也相应产生变化。为了描述信号频谱的谱对称性,定义谱对称偏离系数γ为:
(9)
上式中,fc为载频,h(f)为信号基于EMD的Hilbert边缘谱。谱对称偏离系数γ反映了信号频谱偏离对称情况的度量。
3实验分析
为验证本文方法的有效性,实验中利用本文算法进行特征提取,以基于多项式核函数的SVM作为分类器对提取的特征进行分类实验。通过以下三组实验验证本文算法具有的优势:实验一通过与参考算法的对比,验证本算法在识别精度方面的提升;实验二、三通过比较电台不同条件下的分类识别情况,验证本文算法具有较好的鲁棒性。
本文的实验数据采用的是10部同型号、同批次建伍电台数据,其实验数据采集背景条件如表1所示。

表1 外场实验数据采集环境
在特征提取实验中,使用本文所提出的算法,提取前7层IMF函数的分形特征(包括盒维数、信息维数与Lempel-Ziv复杂度,下同),求出前7层IMF所对应的瞬时频率并提取分形特征,提取Hilbert边缘谱的对称系数与分形特征,结合上述3类特征得到特征向量。在分类实验中将每组电台信号分成200份信号进行实验,随机抽取100份用于训练,剩余的100份用于测试,使用基于多项式的SVM分类器进行分类得到分类结果。
实验一:将电台在不同工作状态下接收到的信息对电台进行分类。接收方式分别为近距离有直达波和远距离无直达波,发射频率分别为160 MHz、410 MHz,在不同说话人的情况下,进行100次分类实验的实验结果如表2所示。
从实验结果中我们可以看出,接收方式为近距离有直达波情况下的识别率平均要高出远距离无直达波,同时较高的发射频率也比低发射频率在识别效果上有所提升。这主要是由于电台有直达波比无直达波的传输信道好,高频信号在传输过程中受干扰程度较小。
为说明本文算法的优势,选择文献[5]中使用EMD分解后提取网格分形维数作为分类特征的算法作为参考算法。采用两种不同的算法提取细微特征,使用基于多项式的SVM分类器进行分类。以识别率为作为衡量标准,比较两种算法在多组信号中分类效果,结果如图3所示。
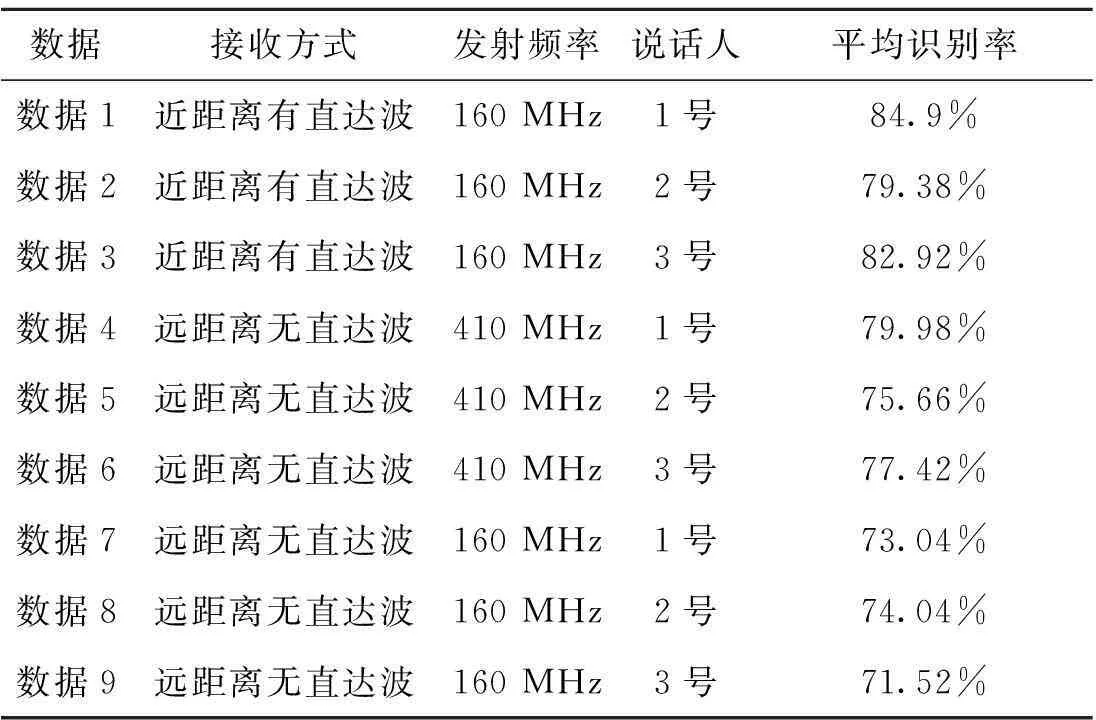
表2 不同工作状态下10部电台的分类结果

图3 两种算法分类效果上的比较Fig.3 Two kinds of algorithm comparing the classification results
从实际电台实验的分类结果可以看出,由于本文算法较参考算法EMD+dim从时域与频域多方面提取特征,并且提取的特征参数种类更多,故本文算法在识别率上较参考算法有较大的提升。
为了验证本文算法具有较好的鲁棒性,通过以下两个实验证明本文算法针对同样电台工作在不同说话人,不同发射频率与不同接收方式的条件下依旧具有较好的识别效果。
实验二:发射机工作频率为W1=160 MHz和W2=410 MHz,接收机接收方式为近距离有直达波和远距离无直达波两种,比较同一说话人在不同工作频率与不同工作方式条件下的电台识别效果。实验方法从分别从不同说话人S1、S2、S3的训练样本中随机抽取100个样本组合成训练集,剩余的100个样本组成测试集,进行100次分类实验,得到的平均分类结果如表3所示。

表3 不同发射频率条件下10部
实验二比较了在说话人一致的情况下,不同的电台发射频率对于电台识别效率的影响。实验结果表明本文算法对于不同工作模式的电台仍然具有较好的识别效果。
实验三:发射机工作频率为160 MHz,接收方式分别为近距离有直达波和远距离无直达波比较同一说话人在不同工作方式条件下的电台识别效果。实验方法同上,得到的平均分类结果如表4所示。
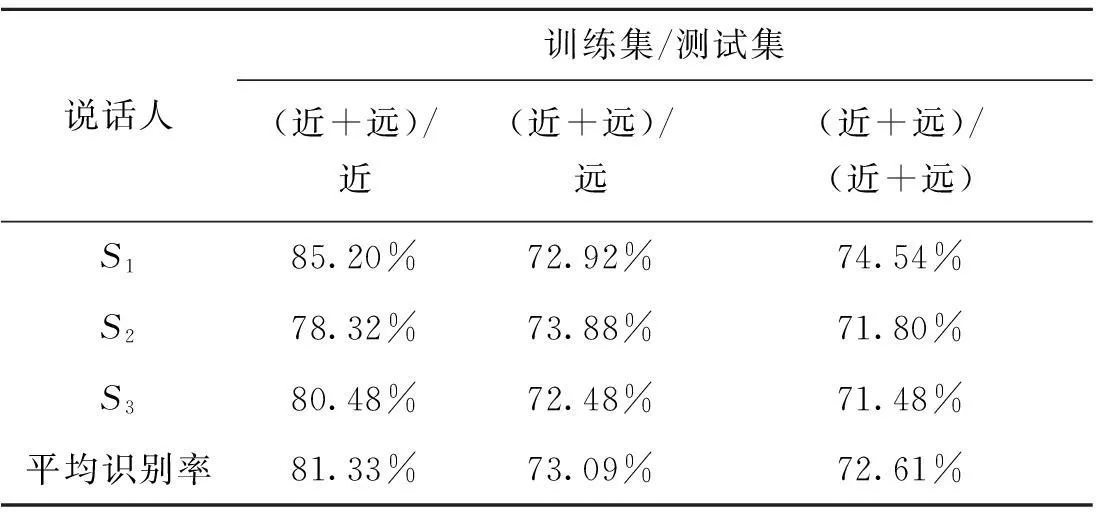
表4 不同接收方式条件下10部
实验三比较了在发射频率相同的情况下,不同接收方式对于电台识别效率的影响。实验结果表明本文算法对于电台更换接收方式的情况下仍有较好的识别效果。
4结论
本文提出了基于EMD分解模型的通信辐射源特征提取方法。该算法通过对原始信号经过EMD分解后得到的IMF进行时域与频域的特征提取,反映出通信辐射源内部细微特性。实验分析表明:该算法在识别精度方面较参考算法有所提升,并且针对电台处于不同工作条件下的识别具有一定的鲁棒性。但由于本文算法建立在EMD模型基础之上,EMD分解消耗的时间相对较多,如何改进EMD分解的终止条件,减少循环迭代次数,提高算法的运行效率仍需进一步研究。
参考文献:
[1]Song C Y, Xu J M,Zhan Y. A Method forSpecific Emitter Identification Based on Empirical Mode Decomposition[C]//Wireless Communications,Networking and Information Security(WCNIS),2010 IEEE International Conference,2010:54-57.
[2]Dudczyk J, Kawalec A. Identification of emitter sources in the aspect of their fractical features[J].Bulletin of thePolish Academy of Sciences Technical Sciences,2013,61(3):623-628.
[3]张旻,钟子发,王若冰.通信电台个体识别技术研究[J].电子学报,2009,37(10):2125-2129.
[4]钱祖平,许渊,卲尉,等.基于高阶谱和时域分析的电台稳态特征提取算法[J].电子与信息学报,2013(7):1599-1605.
[5]陆满君,詹毅,司锡才,等.通信辐射源瞬态特征提取和个体识别方法[J].西安电子科技大学学报(自然科学版),2009,36(4):736-740.
[6] Huang Norden,Shen Zheng,Long Steven R .The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[C]//Proceedings of the Royal Society of London ,1998 ,454 :903-995.
[7]Dan R M, Yang Z J. Feature extraction for hoisting load of multiple rope friction hoist on improved EMD[J]. Journal of China Coal Society, 2014, 39(4): 782-788.
[8]沈路,杨富春,周晓军.基于改进EMD与形态滤波的齿轮故障特征提取[J].振动与冲击,2010(3):154-157.
[9] 侯青剑,王宏力.一种基于EMD的模拟电路故障特征提取方法[J].系统工程与电子技术,2009,31(6):1525-1528.
[10]Du J, Mu Z, Xu Z, et al. Feature extraction in fingerprint of medicinal herbs via EMD and fractal technique[J].International Conference on Biomedical Engineering Informatics ,2011(3):1715-1719.
[11] 梁江海,黄知涛.一种基于经验模态分解的通信辐射源个体识别方法[J],中国电子科学研究院学报,2013,8(4):393-397.
[12]Huang N E, Wu Z, Long S R, et al. On instantaneous frequency[J] Advances in Adaptive Data Analysis,2009:177-229.
A Fractal Feature Extraction Algorithm Based on Empirical Mode Decomposition
GUI Yunchuan1,2, YANG Junan1,2, LV Jijie1,2,WANG Wei1,2
(1.Department of Information Engineering,Electronic Engineering Institute of PLA,Hefei 230037,China;2.Key Laboratory of Electronic Restriction of Anhui Province,Hefei 230037,China)
Abstract:In view of the problem that the accuracy of the individual identification method of communication transmitter is low, and poor in robust, a feature extraction method based on the empirical mode decomposition(EMD) model was proposed in this paper. In this algorithm, fractal features of intrinsic mode function from the time domain and frequency domain was extracted, which combined with the Hilbert marginal spectrum fractal feature and symmetry coefficient to get feature vector. Support vector machine(SVM) was employed to identify transmitter individuals. The experimental results of the classification of the 10 parts of the proposed radio station showed that the algorithm could obtain better classification results without any prior information and had a certain robustness.
Key words:communication transmitter; feature extraction; empirical mode decomposition; fractal feature
中图分类号:TN911.7
文献标志码:A
文章编号:1008-1194(2016)01-0104-05
作者简介:桂云川(1991—),男,江西鹰潭人,硕士研究生,研究方向:通信辐射源特征提取。E-mail:15209831812@163.com。
基金项目:安徽省自然科学基金项目资助(1308085QF99,1408085MKL46)
*收稿日期:2015-11-06
