弥散颗粒对中子学计算影响的初步分析
2016-04-06张知竹倪东洋巨海涛于颖锐
秦 冬,张知竹,倪东洋,巨海涛,于颖锐
(中国核动力研究设计院核反应堆系统设计技术重点实验室,四川成都610041)
弥散颗粒对中子学计算影响的初步分析
秦 冬,张知竹,倪东洋,巨海涛,于颖锐
(中国核动力研究设计院核反应堆系统设计技术重点实验室,四川成都610041)
弥散颗粒燃料是一种先进的燃料元件形式,双重非均匀性是它的固有特性。本文基于弥散型燃料,使用MCNP程序对不同燃料颗粒直径、燃料富集度、燃料相体积、可燃毒物颗粒直径和可燃毒物类型的板栅元进行了分析,研究了双重非均匀性对中子学计算的影响,指出双重非均匀性在一定的尺寸下,对于纯燃料芯体板栅元影响较小,对含有弥散可燃毒物的板栅元影响较大,在反应性计算、临界安全分析时必须加以考虑。
弥散颗粒;双重非均匀性;可燃毒物;计算模型
弥散颗粒燃料是一种先进的燃料元件形式,它由燃料颗粒(U、Pu的化合物)弥散分布在惰性基体材料(如金属、陶瓷或者石墨等非裂变材料)中构成,也被称为惰性基体燃料(Inert matrix fuel)。
弥散型燃料元件在一般非均匀性(燃料芯体、包壳、慢化剂或冷却剂)之外引入了新的非均匀性,即燃料芯体的非均匀性(燃料颗粒弥散分布在基体材料中),形成燃料元件的双重非均匀性。在计算此类燃料元件时如果对燃料芯体采取均匀化混合处理的方式,即将燃料颗粒和基体材料均匀化混合,忽略芯体的非均匀性,有可能低估系统的反应性,造成一定的计算偏差[1]。同时为了控制反应性,在燃料芯体中还会弥散一定数量的可燃毒物,由于可燃毒物颗粒的自屏效应,燃料元件的双重非均匀性会更加强烈,从而对计算结果产生较大影响。
本文基于弥散型燃料,对纯燃料和含有可燃毒物的燃料单板栅元进行了建模计算,研究双重非均匀性对栅元中子学计算的影响。
1 研究内容及条件
基于板型弥散燃料栅元,研究分析不同因素(燃料颗粒直径、燃料富集度、燃料相体积(即燃料颗粒在燃料芯体中的体积份额)、可燃毒物颗粒直径和可燃毒物类型)对栅元中子学计算的影响。
计算分析基于以下条件:(1) 燃料颗粒(UO2微球)直径在75μm~300μm;(2) 可燃毒物颗粒直径在60μm~100μm,毒物类型考虑B4C、Er2O3和Gd2O3。本文的计算主要使用MCNP[2]程序。
2 纯燃料计算分析
2.1 计算模型
在一般计算时,对弥散型燃料芯体通常采取均匀化混合处理的方式,下文中称为均匀模型。本文为了准确地考虑弥散型燃料板栅元双重非均匀性的特性,借助MCNP几何描述功能将芯体中的UO2微球独立描述,下文中称为颗粒模型。
在建立燃料芯体颗粒模型时,采取如下设置:(1) UO2微球直径在目标值附近(75μm、150μm和300μm左右);(2) 保证芯体中各材料体积与实际一致;(3) 保证颗粒栅元尺寸合适,尽量减少空间截断的干扰。
同一燃料相体积的不同UO2微球直径的板栅元示意见图1,图示为板型燃料组件的一个最小重复结构单板栅元的截面,中心含有球形颗粒的是燃料芯体部分,燃料芯体外面分别为包壳和轻水慢化剂,栅元采用全反射边界条件。需要指出的是,由于计算手段的限制,目前还无法考虑燃料芯体中UO2微球直径及空间分布的随机效应。

图1 不同UO2颗粒直径板栅元模型Fig.1 Plate cell model of different UO2 particle diameter
2.2 计算结果
基于上述的燃料芯体颗粒模型,对中等燃料富集度情况下不同燃料相体积、不同UO2颗粒直径的燃料板栅元进行了计算,结果如表1所示。

表1 不同燃料相体积颗粒模型计算结果(中等燃料富集度)
注:*:颗粒模型1、2、3分别指图1中UO2颗粒直径为75μm、150μm和300μm附近的计算模型,下同。
**:(颗粒模型计算结果/均匀模型计算结果-1)×100%,下同。
从表1中可见,与均匀模型计算结果相比,随着UO2微球直径不断增大,其keff也不断增加。即与芯体材料的均匀化混合处理相比,UO2微球独立处理所体现的双重非均匀效应使得计算结果变大。
UO2微球的独立存在,理论上会产生空间自屏效应:一方面减少了内层燃料对热中子的吸收,减小了热中子利用系数,带来负面的影响;另一方面也减少了燃料对中子的共振吸收,使得共振中子逃脱共振俘获概率增加,从而带来正面的影响。UO2的热中子(0.0253eV)宏观总截面为0.542(102m-1)[3],总平均自由程约为1.845cm,而燃料芯体中的UO2微球直径远小于这个尺度。因此热中子利用系数的减小不是UO2微球空间自屏效应影响的主要方面。能量为6.67eV的共振中子在铀块中的平均自由程为0.003cm[3],即30μm。UO2微球直径比该值大,因此减少共振中子吸收是空间自屏效应影响的主要方面。因此随着颗粒直径增加,共振中子吸收的减小,keff随之变大。
从表1的结果也可以看出:燃料微球的直径越大,空间自屏效应越强,颗粒模型和均匀模型的计算偏差就越大。但是这种影响总体上相对较小,对于中等燃料富集度、不同燃料相体积的情况,燃料芯体均匀化处理带来的计算偏差在0.24%~0.10%,几乎可以忽略。
燃料微球直径相近、不同燃料相体积时颗粒模型和均匀模型的偏差也有不同。燃料微球直径为75μm左右时,低、中、高燃料相体积的颗粒模型和均匀模型的计算偏差分别为0.05%、0.04%和0.03%。
颗粒模型和均匀模型的计算偏差主要来自于燃料芯体中燃料微球存在形成的空间自屏效应。在燃料微球直径一定的情况下:燃料相体积越小,燃料微球分布越稀疏(假设均匀规则分布),其非均匀效应相对就越明显,模型之间的计算偏差就相对越大;燃料相体积越大,燃料微球分布越密集,其非均匀效应就越小,模型之间的计算偏差就相对越小。
表2给出了低燃料相体积情况下,不同燃料富集度时不同模型的计算结果。
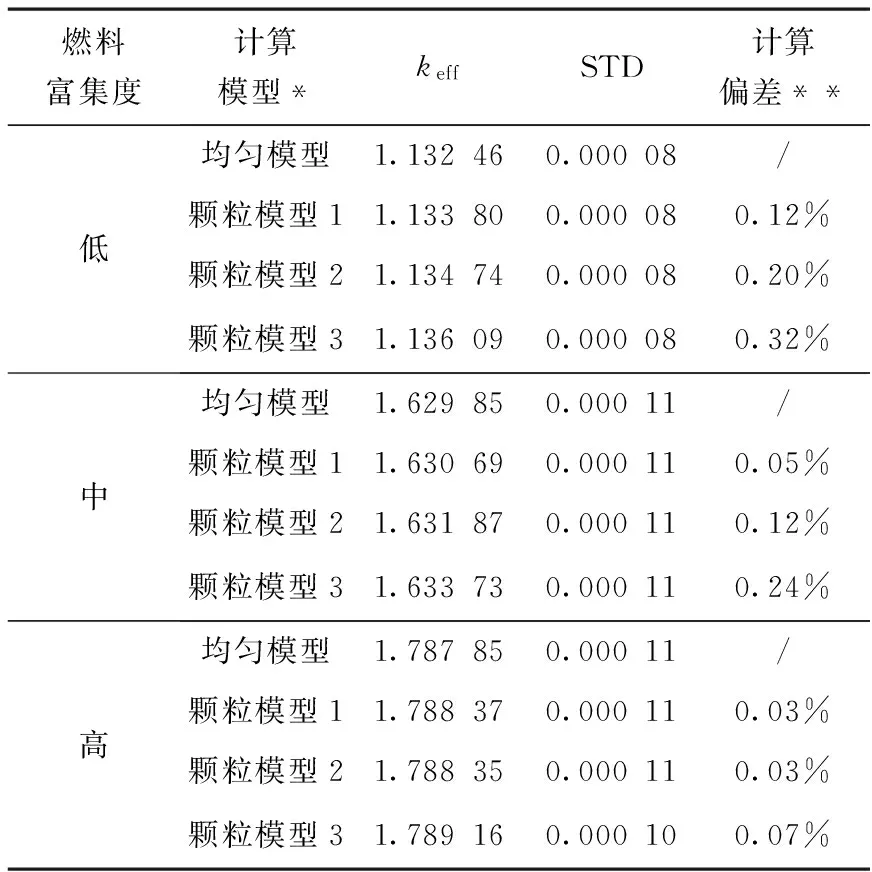
表2 不同燃料富集度颗粒模型计算结果(低燃料相体积)
从表2结果可见,相近燃料微球直径、不同燃料富集度时颗粒模型与均匀模型的结果偏差也有不同。燃料微球直径为75μm左右时,低、中、高燃料富集度不同模型的计算偏差分别为0.12%、0.05%和0.03%。燃料微球直径为300μm左右时,计算偏差分别为0.32%、0.24%、0.07%。即颗粒直径一定时,计算偏差随燃料富集度增大而逐渐减小。
颗粒模型和均匀模型的计算偏差主要来自于燃料芯体中燃料微球非均匀分布形成的空间自屏效应,进一步而言是空间自屏减小了共振中子的吸收使得计算keff更大。燃料相体积一定时:低富集度燃料中的238U更多,自屏效应的效果就相对更加明显,因此颗粒模型和均匀模型计算结果的偏差就相对更大;高富集度燃料中的238U相对较少,自屏效应的效果相对不太明显,因此颗粒模型和均匀模型计算结果的偏差相对就较小。
2.3 小结
本节对不同UO2微球直径、燃料相体积、燃料富集度的板栅元keff进行了建模计算,得到以下结论:(1) 颗粒模型能够反映弥散燃料UO2微球的空间自屏效应,计算结果比均匀模型偏大,并且颗粒直径越大,与均匀模型的偏差就越大;(2) 燃料颗粒直径一定时:燃料相体积越大,与均匀模型的计算偏差越小;燃料富集度越高,与均匀模型的计算偏差越小;(3) 本文中纯燃料芯体板栅元颗粒模型反应的空间自屏效应影响较小,在计算时仍可采用芯体均匀化混合的处理方式。
3 含弥散毒物燃料计算分析
3.1 计算模型
含弥散毒物的板栅元颗粒模型如图2所示。在建模过程中设置可燃毒物颗粒直径设置在目标值附近(60μm、80μm和100μm),其他要求同燃料颗粒模型。

图2 含弥散毒物颗粒模型Fig.2 Particle Model with dispersed burnable poison
本文此处计算时仅考虑单一燃料微球直径。由于计算手段限制,目前还无法考虑可燃毒物颗粒直径及空间的随机分布效应。可燃毒物颗粒板栅元示意见图3。

图3 含弥散毒物燃料板栅元模型Fig.3 Plate cell model with dispersed burnable poison
3.2 计算结果
基于上述模型,对含有一定相体积B4C颗粒的燃料板栅元进行了计算,同时为了比较,还计算了均匀模型,结果如表3所示。

表3 含弥散B4C毒物板栅元计算结果
注:*:颗粒模型1、2、3分别指图2中可燃毒物颗粒直径分别为60μm、80μm和100μm的3个计算模型。
从表3结果可见,可燃毒物颗粒模型计算结果和均匀模型相比差别较大,并且这种差别随着毒物颗粒直径的变大而增加。毒物颗粒直径在100μm时的单板栅元计算结果与均匀模型的结果偏差超过了7%,双重非均匀性的影响不容忽视。
可燃毒物颗粒的独立存在,由于其对中子的较强吸收,会在颗粒中形成较强的自屏效应,使的颗粒内部的毒物对中子的吸收变弱,使得毒物的有效吸收截面减小。而均匀模型的计算结果会高估系统的吸收,使得keff计算值偏小。
对含弥散可燃毒物燃料板分别考虑UO2微球和B4C颗粒导致了建模相对复杂。而根据前文的分析,燃料颗粒本身的空间自屏效应相对很小,因此含可燃毒物燃料板计算偏差的主要原因是其中所含的B4C颗粒的自屏效应。
因此仅对B4C毒物进行颗粒建模,对UO2微球采取和锆基均匀混合的处理方式。其中B4C毒物颗粒的直径分别取80μm左右、40μm左右、20μm左右和10μm左右。毒物颗粒直径80μm的板栅元示意见图4,计算结果见表4。

图4 D80板栅元模型Fig.4 Plate cell model of D80
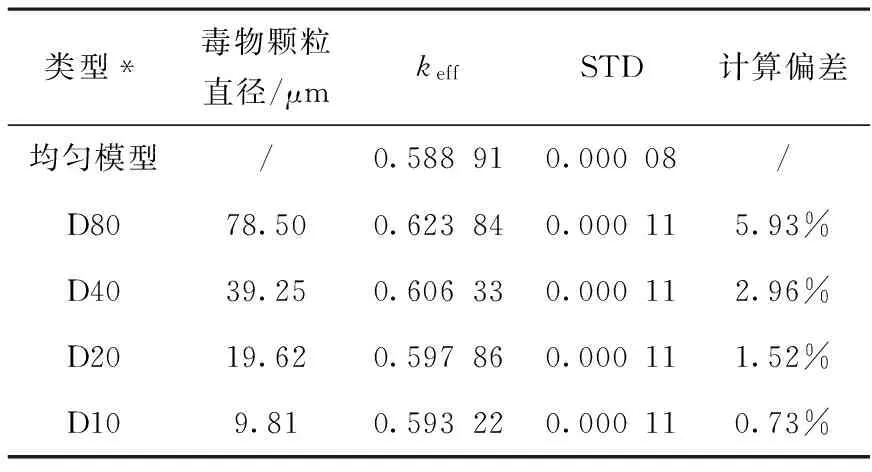
表4 仅考虑毒物颗粒的计算结果
*:D80模型指毒物颗粒直径为80μm,其他类似。
从表4结果可见,在仅考虑B4C毒物颗粒情况下,直径在80μm左右的计算结果和颗粒模型2(毒物颗粒直径在80μm左右)相当接近,其keff分别为0.62384和0.62278,两者偏差不到0.2%。
同时也看出,随着B4C毒物颗粒直径的减小,其结果和均匀模型越来越接近。当毒物颗粒直径为10μm左右时,计算结果为0.59322,和均匀模型的计算结果偏差为0.73%。这说明如果继续采取均匀模型的计算方法,B4C颗粒的直径必须要减小到10μm之下才不会引起较大的计算偏差。
除了B4C外,本文还对Er2O3和Gd2O3做弥散可燃毒物的情况进行了计算分析。计算结果见表5和表6。

表5 含弥散Er2O3毒物板栅元计算结果
颗粒尺寸相近情况下,可燃毒物对中子的吸收能力越强,空间自屏效应越明显。B4C、Gd2O3和Er2O3中,Gd2O3中子吸收能力最强,所以空间自屏效应也最强。Er2O3的中子吸收能力最弱,其空间自屏效应也最弱。毒物颗粒同为80μm左右时,Gd2O3毒物颗粒模型和均匀模型的计算偏差超过了18%,而Er2O3颗粒模型和均匀模型的偏差仅为0.5%左右。
3.3 修正方法初步研究
含弥散可燃毒物颗粒的燃料芯体,必须采用颗粒模型才能较为准确的进行计算,而目前一般的栅元计算程序无法进行颗粒模型的建模,难以考虑双重非均匀性,因此若继续使用均匀模型计算则必须考虑一定的修正。
引入可燃毒物的自屏因子fs(t)[3],它的定义为:
由此可见,可燃毒物有效吸收截面为:
基于3.2节中D80板栅元模型,利用MCNP程序F4计数卡通量统计功能,统计毒物颗粒和燃料中的平均中子通量,计算可燃毒物的自屏因子。
四群及七群通量自屏因子计算结果过见表7~表8。基于表中的自屏因子对MCNP数据库中10B吸收截面进行修正,然后再用均匀模型进行计算,其结果分别为0.61380(四群修正)和0.62075(七群修正),与D80颗粒模型计算结果0.62384的偏差分别为-1.60%和-0.495%。结果表明这种修正既必要,也有一定的准确性。

表7 四群通量自屏因子

表8 七群通量自屏因子
3.4 小结
本节对不同弥散可燃毒物颗粒直径、类型的燃料单板栅元进行了建模计算,得到以下结论:
(1) 可燃毒物颗粒空间自屏效应较强,与均匀模型的计算结果差别很大;(2) 可燃毒物颗粒直径越大,空间自屏效应越强,与均匀模型的计算结果差别越大;颗粒直径一定时,可燃毒物中子吸收能力越强,与均匀模型的计算偏差越大;(3) 在计算中必须考虑可燃毒物的颗粒效应,使用均匀模型计算时可通过自屏因子进行修正,可较好地改善计算精度。
4 结论
本文基于弥散型燃料栅元,使用MCNP程序研究分析不同因素(燃料颗粒直径、燃料富集度、燃料相体积、可燃毒物颗粒直径和可燃毒物类型)对栅元中子学计算的影响,得到了以下结论:在一定的尺寸下,(1) 本文中纯燃料芯体双重非均匀性对中子学计算的影响较小,计算时仍可采用芯体材料均匀化的处理方式;(2) 含可燃毒物颗粒燃料芯体双重非均匀性对中子学计算的影响很大,若采用材料均匀化的处理方式会引入较大计算偏差;(3) 对于含可燃毒物颗粒栅元使用均匀模型计算时通过自屏因子进行修正,可较好地改善计算精度。
[1] 常鸿. 等.球床式高温气冷堆初次临界物理计算的蒙特卡罗方法模型分析[J].核动力工程,Vol.26. No.5,2005.
[2] Judith F Briesmeister,Editor.MCNPTM-A General Monte Carlo N-Particle Transport Code,Version 4C.Los Alamos National Laboratory report LA-13709-M,2000.
[3] 谢仲生,吴宏春,张少泓.核反应堆物理分析(修订版)[M].西安:西安交通大学出版社,2004.
Preliminary Analysis of Dispersion Particle Effects on Neutronic Calculation
QIN Dong,ZHANG Zhi-zhu,NI Dong-yang,JU Hai-tao,YU Ying-rui
(1.Science and Technology on Reactor Design Technology Laboratory,Nuclear Power Institute of China,Chengdu,610041,China)
The dispersion particle fuel is an advanced fuel element form,and it has an intrinsic characteristic of double heterogeneity. This paper studies the double heterogeneity effect on neutronic in dispersion fuel element by analyzing fuel cell with different fuel particle diameters、enrichments、volume fractions、poison particle diameters、poison types. The result shows that the double heterogeneity effect is smaller in dispersion fuel element with only fuel particle,but is bigger in dispersion fuel element with poison particle,which must be considered in reactivity and critical safety analysis.
Double heterogeneity;Fuel particle;Burnable poison;Calculation Model
2016-03-10
秦 冬(1983—),男,江苏扬州人,工程师,硕士,现从事反应堆物理方向的工作
TL329
A
0258-0918(2016)04-0470-06
